SP
Sanjeev Prabhakar
Sun, Nov 17, 2024 4:12 PM
I have checked again, the tooth angles in both inner side and outer side
are exactly 80.6 and the distortion is not due to the projection on the
cylinder, it is due to the cone angle and compound effect of the 2 angles.
In my case when I keep the cone angle at 32.5 deg all the angles exactly
match the defined numbers.
I have checked again, the tooth angles in both inner side and outer side
are exactly 80.6 and the distortion is not due to the projection on the
cylinder, it is due to the cone angle and compound effect of the 2 angles.
In my case when I keep the cone angle at 32.5 deg all the angles exactly
match the defined numbers.

AM
Adrian Mariano
Sun, Nov 17, 2024 4:26 PM
Sanjeev, I didn't see that you stated what your definition of "cone angle"
is. In my case, it's not an angle you can easily see in the model, since
it is through the CENTER of the tooth. And yes, the deviation I was
describing with cone angle in my model is due to the effect of compound
angles, that is, if you measure tooth angle as angle between the planes of
the tooth then that changes with rising cone angle because of the compound
angle effect.
Why is 32.5 degrees a magical cone angle for your model?
On Sun, Nov 17, 2024 at 11:13 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I have checked again, the tooth angles in both inner side and outer side
are exactly 80.6 and the distortion is not due to the projection on the
cylinder, it is due to the cone angle and compound effect of the 2 angles.
In my case when I keep the cone angle at 32.5 deg all the angles exactly
match the defined numbers.
Sanjeev, I didn't see that you stated what your definition of "cone angle"
is. In my case, it's not an angle you can easily see in the model, since
it is through the CENTER of the tooth. And yes, the deviation I was
describing with cone angle in my model is due to the effect of compound
angles, that is, if you measure tooth angle as angle between the planes of
the tooth then that changes with rising cone angle because of the compound
angle effect.
Why is 32.5 degrees a magical cone angle for your model?
On Sun, Nov 17, 2024 at 11:13 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I have checked again, the tooth angles in both inner side and outer side
> are exactly 80.6 and the distortion is not due to the projection on the
> cylinder, it is due to the cone angle and compound effect of the 2 angles.
> In my case when I keep the cone angle at 32.5 deg all the angles exactly
> match the defined numbers.
>
>

SP
Sanjeev Prabhakar
Sun, Nov 17, 2024 4:37 PM
Oh I think the explanation I sent earlier had some pictures which exceeded
the acceptable size for mails here and did not reach anyone.
The angle tooth makes with x-y plane is the angle of the tooth.
32.5 is only for the case where tooth angle is 80 degree, number of teeth
are 50 and cone angle if set to 32.5.
For different configurations this might change.
Also I did not try to measure the angle if tooth face is intersected by a
vertical plane perpendicular to tooth line joining the inner and outer
points.
Maybe that would be correct angle. But I am not sure
On Sun, 17 Nov, 2024, 9:57 pm Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I didn't see that you stated what your definition of "cone angle"
is. In my case, it's not an angle you can easily see in the model, since
it is through the CENTER of the tooth. And yes, the deviation I was
describing with cone angle in my model is due to the effect of compound
angles, that is, if you measure tooth angle as angle between the planes of
the tooth then that changes with rising cone angle because of the compound
angle effect.
Why is 32.5 degrees a magical cone angle for your model?
On Sun, Nov 17, 2024 at 11:13 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have checked again, the tooth angles in both inner side and outer side
are exactly 80.6 and the distortion is not due to the projection on the
cylinder, it is due to the cone angle and compound effect of the 2 angles.
In my case when I keep the cone angle at 32.5 deg all the angles exactly
match the defined numbers.
Oh I think the explanation I sent earlier had some pictures which exceeded
the acceptable size for mails here and did not reach anyone.
The angle tooth makes with x-y plane is the angle of the tooth.
32.5 is only for the case where tooth angle is 80 degree, number of teeth
are 50 and cone angle if set to 32.5.
For different configurations this might change.
Also I did not try to measure the angle if tooth face is intersected by a
vertical plane perpendicular to tooth line joining the inner and outer
points.
Maybe that would be correct angle. But I am not sure
On Sun, 17 Nov, 2024, 9:57 pm Adrian Mariano, <avm4@cornell.edu> wrote:
> Sanjeev, I didn't see that you stated what your definition of "cone angle"
> is. In my case, it's not an angle you can easily see in the model, since
> it is through the CENTER of the tooth. And yes, the deviation I was
> describing with cone angle in my model is due to the effect of compound
> angles, that is, if you measure tooth angle as angle between the planes of
> the tooth then that changes with rising cone angle because of the compound
> angle effect.
>
> Why is 32.5 degrees a magical cone angle for your model?
>
> On Sun, Nov 17, 2024 at 11:13 AM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> I have checked again, the tooth angles in both inner side and outer side
>> are exactly 80.6 and the distortion is not due to the projection on the
>> cylinder, it is due to the cone angle and compound effect of the 2 angles.
>> In my case when I keep the cone angle at 32.5 deg all the angles exactly
>> match the defined numbers.
>>
>>

RW
Raymond West
Sun, Nov 17, 2024 5:43 PM
Afaik, The Hirth joint was invented in 1928, and was very simple to
manufacture, with the machinery available at the time. I'm pretty sure,
that none of the detail On Hirth Ring Couplings: Design Principles
Including the Effect of Friction https://www.mdpi.com/2076-0825/7/4/79
for example, was known. I'm not sure why it is being made so complicated
on here.
On 17/11/2024 13:22, Michael Möller via Discuss wrote:
Afaik, The Hirth joint was invented in 1928, and was very simple to
manufacture, with the machinery available at the time. I'm pretty sure,
that none of the detail On Hirth Ring Couplings: Design Principles
Including the Effect of Friction <https://www.mdpi.com/2076-0825/7/4/79>
for example, was known. I'm not sure why it is being made so complicated
on here.
On 17/11/2024 13:22, Michael Möller via Discuss wrote:
>
>
>

FH
Father Horton
Sun, Nov 17, 2024 6:08 PM
If it’s worth doing, it’s worth overdoing.
If it’s worth doing, it’s worth overdoing.

AM
Adrian Mariano
Sun, Nov 17, 2024 6:46 PM
Ray, I have to say that I've found the complexity lurking in this hirth
joint to be kind of baffling. When I saw Bob's first attempt I
immediately thought Bob was massively overcomplicating things. But I was
wrong. It seems like it should be very simple, and yet it seems to be
remarkably subtle and complicated. We're not "making" it that
way---that's just the way it is. I thought it was trivial and wrote a
straight forward code and then found that it didn't work in various
cases---it was wrong, in other words, and getting it right is hard. Or at
least I didn't find an easy way to get it right, and neither did Bob. And
when I say it was wrong, I mean that the joint didn't mate properly.
Clearly something different happens if you approach the design with "I have
a 60 deg milling cutter, how do I cut a 100 tooth hirth joint" than "I want
to construct a mathematical model that makes a generic version of this
joint". I think another factor is that a lot of the subtlety results in
errors that become small when there are lots of teeth. I see potential
interesting applications for this joint with small numbers of teeth like
perhaps 8 or 4 to create mechanisms that lock into a small number of
positions, so I don't want to ignore those small tooth count cases.
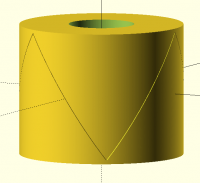
Regarding tooth angle, I attempted to measure it at the tooth ridge with
nominal tooth angle set to 60 and zero cone angle. With four teeth I get
76.8 deg instead of 60 deg. With 44 teeth I get 60.16 deg. With 144 teeth
it's 60.01 deg. If I raise the cone angle to 30 deg then I actually get
60.4 in the 4 tooth case, but in the 44 tooth case it's now 65.5 deg and
with 144 teeth it's 66.8 deg. Why does the 30 deg cone angle make the 4
tooth case so close to the nominal angle? It's because the tooth ridge in
this case is very close to parallel to the xy plane, which matches the
design angle reference for the construction of the triangle. Here's a
picture (4 teeth, 30 deg cone angle, 60 deg nominal tooth angle):
[image: image.png]
So it seems like the deviation of tooth angle for small tooth count has to
do with fitting the teeth around a circle. When you have lots of teeth,
it's approximately like fitting the teeth onto a line and nothing weird
happens, but when you curve just 4 teeth around a circle, the angles no
longer add up as expected for flat geometry, resulting in an alteration of
the actual realized tooth angle. So to produce teeth that match the
nominal angle there are two corrections needed. One is a correction for
fitting a linear arrangement of triangles around a circle, with increasing
correction as the number of teeth shrinks. The other one has to do with
cone angle, and at least for my definition of cone angle, the correction
looks like it gets smaller and then larger again as you increase the cone
angle---at least for the small tooth count case.
On Sun, Nov 17, 2024 at 12:44 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
Afaik, The Hirth joint was invented in 1928, and was very simple to
manufacture, with the machinery available at the time. I'm pretty sure,
that none of the detail On Hirth Ring Couplings: Design Principles
Including the Effect of Friction https://www.mdpi.com/2076-0825/7/4/79
for example, was known. I'm not sure why it is being made so complicated on
here.
On 17/11/2024 13:22, Michael Möller via Discuss wrote:
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Ray, I have to say that I've found the complexity lurking in this hirth
joint to be kind of baffling. When I saw Bob's first attempt I
immediately thought Bob was massively overcomplicating things. But I was
wrong. It seems like it should be very simple, and yet it seems to be
remarkably subtle and complicated. We're not "making" it that
way---that's just the way it is. I thought it was trivial and wrote a
straight forward code and then found that it didn't work in various
cases---it was wrong, in other words, and getting it right is hard. Or at
least I didn't find an easy way to get it right, and neither did Bob. And
when I say it was wrong, I mean that the joint didn't mate properly.
Clearly something different happens if you approach the design with "I have
a 60 deg milling cutter, how do I cut a 100 tooth hirth joint" than "I want
to construct a mathematical model that makes a generic version of this
joint". I think another factor is that a lot of the subtlety results in
errors that become small when there are lots of teeth. I see potential
interesting applications for this joint with small numbers of teeth like
perhaps 8 or 4 to create mechanisms that lock into a small number of
positions, so I don't want to ignore those small tooth count cases.
Regarding tooth angle, I attempted to measure it at the tooth ridge with
nominal tooth angle set to 60 and zero cone angle. With four teeth I get
76.8 deg instead of 60 deg. With 44 teeth I get 60.16 deg. With 144 teeth
it's 60.01 deg. If I raise the cone angle to 30 deg then I actually get
60.4 in the 4 tooth case, but in the 44 tooth case it's now 65.5 deg and
with 144 teeth it's 66.8 deg. Why does the 30 deg cone angle make the 4
tooth case so close to the nominal angle? It's because the tooth ridge in
this case is very close to parallel to the xy plane, which matches the
design angle reference for the construction of the triangle. Here's a
picture (4 teeth, 30 deg cone angle, 60 deg nominal tooth angle):
[image: image.png]
So it seems like the deviation of tooth angle for small tooth count has to
do with fitting the teeth around a circle. When you have lots of teeth,
it's approximately like fitting the teeth onto a line and nothing weird
happens, but when you curve just 4 teeth around a circle, the angles no
longer add up as expected for flat geometry, resulting in an alteration of
the actual realized tooth angle. So to produce teeth that match the
nominal angle there are two corrections needed. One is a correction for
fitting a linear arrangement of triangles around a circle, with increasing
correction as the number of teeth shrinks. The other one has to do with
cone angle, and at least for my definition of cone angle, the correction
looks like it gets smaller and then larger again as you increase the cone
angle---at least for the small tooth count case.
On Sun, Nov 17, 2024 at 12:44 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
> Afaik, The Hirth joint was invented in 1928, and was very simple to
> manufacture, with the machinery available at the time. I'm pretty sure,
> that none of the detail On Hirth Ring Couplings: Design Principles
> Including the Effect of Friction <https://www.mdpi.com/2076-0825/7/4/79>
> for example, was known. I'm not sure why it is being made so complicated on
> here.
>
> On 17/11/2024 13:22, Michael Möller via Discuss wrote:
>
>
>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

RW
Raymond West
Sun, Nov 17, 2024 9:15 PM
Hi Adrian,
The code I sent seemed to be OK for anything more than two teeth. Maybe
if I explain how I think it would have been originally made will let you
see where you are getting odd angles. The first requirement would be a
grinding wheel. (I would guess that it was most likely a milling cutter,
and material brass, but never mind, same principle.) The standard angles
for such discs would either be 90 degree or 60 degree (inclusive angle),
others would most likely be more expensive. This would be a disc, with a
v edge (at 90 or 60 degrees). The edge of the disc would be rounded,
since a pointed edge would not last long. This would be used in a
horizontal grinder, the disc can be raised or lowered, and the bed
traversed backwards and forwards under the wheel. A piece of steel,
fixed to the bed could thus have a v groove ground into it, and the
profile, if no sideways movement, would be the inverse of the grinding
disk, it would have a rounded bottom (fillet) to the groove.
Now, if you have a rotary table, then you can clamp a round piece of
steel to that, and rotate the table a certain part of a revolution. So,
say, move in 30 degree steps, and you will get 6 v grooves, crossing in
the centre of the stock piece (or 12 meeting at the centre...) as you
traverse the piece at the fixed angle beneath the grinding disc.
Now, wedge up one end of the rotary table. A new piece of stock will
give you 12 v grooves, say, but shallower towards the centre. If you
make it, such that the grooves are at zero depth at the centre, and full
depth at the edge, and there are the correct number of grooves, then
two such pieces will mesh together, and tend to self centre. Of course,
the bottom of grooves are filleted due to the shape of the grinding
wheel. The fillet will be a constant width. To get two such pieces to
fit together, the peaks need to be rounded over, but flattening them is
simpler, and in some ways better (else the point of the mating ridge
bottoms out on the fillet). The centres of the round stock pieces can be
machined away, since there is little force transmitted there, and for
other reasons. So, simple calculations can be made, depending on the
tooling available, size of desired coupling joint and number of teeth, etc.
Say we have a work piece diameter 40, and a grinding disc, say, width 8,
and 90 degree angle. We can calculate the minimum number of teeth from
d=40 and chord = 8. The maximum will depend on the radius of the 90
degree edge of the grinding wheel (which creates the fillet - we don't
want all fillet!), but let's say 50. That means the rotary table
increments must be in steps of 360/50 =7.2 degrees. If we were going
full depth of cut, then the maximum depth would be 4 (angle of 90
degrees), and 8 between peaks (but we can't go full depth at 7.2degrees).
So, given the length of chord, and diameter of work, we can find the
number of chords, n, from d=(chord/ (sin(180/n))) we can solve that for
chord, and then the height of the ridge will be half of the chord length
(90 degree angle to wheel)- the assumption is that the grinding wheel
edge is pointed, not rounded.
Now, we want the grinding wheel to cut the depth calculated at the edge
of the work piece, but just touch the centre of the workpiece, so we can
calculate that we need to fix it at an angle that is
ASIN(ridge_height/2)/diam).
That will give a self centring matching Hirth joints, which afaik
complies with the 1928 original specification.
For the purposes of calculation ignore the radius at the bottom of the
grooves - that will depend on the wheel profile. As to all intents and
purposes, the bottom of the fillet will be parallel to the bottom of the
estimated groove, so the angle to the horizontal will be the same. The
top of the flattened ridge can be wider than the width of the fillet,
but the edges of the flat will be parallel, too.
Like most things, it starts off simple, then gets overcomplicated, to
the state that it becomes difficult to see what was the fundamental
reason for its existence in the first place. I would guess, that Hirth,
being a practical engineer, just made it in the workshop, then decided
to document it afterwards, most likely quicker than calculating angles,
etc., back then.
I think, as soon as you change the design so that the matching parts are
not identical, or do not have straight and flat flanks to the ridges,
then it is no longer a Hirth coupling.
On 17/11/2024 18:46, Adrian Mariano wrote:
Ray, I have to say that I've found the complexity lurking in this
hirth joint to be kind of baffling. When I saw Bob's first attempt I
immediately thought Bob was massively overcomplicating things. But I
was wrong. It seems like it should be very simple, and yet it seems
to be remarkably subtle and complicated. We're not "making" it that
way---that's just the way it is. I thought it was trivial and wrote a
straight forward code and then found that it didn't work in various
cases---it was wrong, in other words, and getting it right is hard.
Or at least I didn't find an easy way to get it right, and neither did
Bob. And when I say it was wrong, I mean that the joint didn't mate
properly. Clearly something different happens if you approach the
design with "I have a 60 deg milling cutter, how do I cut a 100 tooth
hirth joint" than "I want to construct a mathematical model that makes
a generic version of this joint". I think another factor is that a
lot of the subtlety results in errors that become small when there are
lots of teeth. I see potential interesting applications for this
joint with small numbers of teeth like perhaps 8 or 4 to create
mechanisms that lock into a small number of positions, so I don't want
to ignore those small tooth count cases.
Regarding tooth angle, I attempted to measure it at the tooth ridge
with nominal tooth angle set to 60 and zero cone angle. With four
teeth I get 76.8 deg instead of 60 deg. With 44 teeth I get 60.16
deg. With 144 teeth it's 60.01 deg. If I raise the cone angle to 30
deg then I actually get 60.4 in the 4 tooth case, but in the 44 tooth
case it's now 65.5 deg and with 144 teeth it's 66.8 deg. Why does
the 30 deg cone angle make the 4 tooth case so close to the nominal
angle? It's because the tooth ridge in this case is very close to
parallel to the xy plane, which matches the design angle reference for
the construction of the triangle. Here's a picture (4 teeth, 30 deg
cone angle, 60 deg nominal tooth angle):
image.png
So it seems like the deviation of tooth angle for small tooth count
has to do with fitting the teeth around a circle. When you have lots
of teeth, it's approximately like fitting the teeth onto a line and
nothing weird happens, but when you curve just 4 teeth around a
circle, the angles no longer add up as expected for flat geometry,
resulting in an alteration of the actual realized tooth angle. So to
produce teeth that match the nominal angle there are two corrections
needed. One is a correction for fitting a linear arrangement of
triangles around a circle, with increasing correction as the number of
teeth shrinks. The other one has to do with cone angle, and at least
for my definition of cone angle, the correction looks like it gets
smaller and then larger again as you increase the cone angle---at
least for the small tooth count case.
On Sun, Nov 17, 2024 at 12:44 PM Raymond West via Discuss
discuss@lists.openscad.org wrote:
Afaik, The Hirth joint was invented in 1928, and was very simple
to manufacture, with the machinery available at the time. I'm
pretty sure, that none of the detail On Hirth Ring Couplings:
Design Principles Including the Effect of Friction
<https://www.mdpi.com/2076-0825/7/4/79> for example, was known.
I'm not sure why it is being made so complicated on here.
On 17/11/2024 13:22, Michael Möller via Discuss wrote:
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Hi Adrian,
The code I sent seemed to be OK for anything more than two teeth. Maybe
if I explain how I think it would have been originally made will let you
see where you are getting odd angles. The first requirement would be a
grinding wheel. (I would guess that it was most likely a milling cutter,
and material brass, but never mind, same principle.) The standard angles
for such discs would either be 90 degree or 60 degree (inclusive angle),
others would most likely be more expensive. This would be a disc, with a
v edge (at 90 or 60 degrees). The edge of the disc would be rounded,
since a pointed edge would not last long. This would be used in a
horizontal grinder, the disc can be raised or lowered, and the bed
traversed backwards and forwards under the wheel. A piece of steel,
fixed to the bed could thus have a v groove ground into it, and the
profile, if no sideways movement, would be the inverse of the grinding
disk, it would have a rounded bottom (fillet) to the groove.
Now, if you have a rotary table, then you can clamp a round piece of
steel to that, and rotate the table a certain part of a revolution. So,
say, move in 30 degree steps, and you will get 6 v grooves, crossing in
the centre of the stock piece (or 12 meeting at the centre...) as you
traverse the piece at the fixed angle beneath the grinding disc.
Now, wedge up one end of the rotary table. A new piece of stock will
give you 12 v grooves, say, but shallower towards the centre. If you
make it, such that the grooves are at zero depth at the centre, and full
depth at the edge, and there are the correct number of grooves, then
two such pieces will mesh together, and tend to self centre. Of course,
the bottom of grooves are filleted due to the shape of the grinding
wheel. The fillet will be a constant width. To get two such pieces to
fit together, the peaks need to be rounded over, but flattening them is
simpler, and in some ways better (else the point of the mating ridge
bottoms out on the fillet). The centres of the round stock pieces can be
machined away, since there is little force transmitted there, and for
other reasons. So, simple calculations can be made, depending on the
tooling available, size of desired coupling joint and number of teeth, etc.
Say we have a work piece diameter 40, and a grinding disc, say, width 8,
and 90 degree angle. We can calculate the minimum number of teeth from
d=40 and chord = 8. The maximum will depend on the radius of the 90
degree edge of the grinding wheel (which creates the fillet - we don't
want all fillet!), but let's say 50. That means the rotary table
increments must be in steps of 360/50 =7.2 degrees. If we were going
full depth of cut, then the maximum depth would be 4 (angle of 90
degrees), and 8 between peaks (but we can't go full depth at 7.2degrees).
So, given the length of chord, and diameter of work, we can find the
number of chords, n, from d=(chord/ (sin(180/n))) we can solve that for
chord, and then the height of the ridge will be half of the chord length
(90 degree angle to wheel)- the assumption is that the grinding wheel
edge is pointed, not rounded.
Now, we want the grinding wheel to cut the depth calculated at the edge
of the work piece, but just touch the centre of the workpiece, so we can
calculate that we need to fix it at an angle that is
ASIN(ridge_height/2)/diam).
That will give a self centring matching Hirth joints, which afaik
complies with the 1928 original specification.
For the purposes of calculation ignore the radius at the bottom of the
grooves - that will depend on the wheel profile. As to all intents and
purposes, the bottom of the fillet will be parallel to the bottom of the
estimated groove, so the angle to the horizontal will be the same. The
top of the flattened ridge can be wider than the width of the fillet,
but the edges of the flat will be parallel, too.
Like most things, it starts off simple, then gets overcomplicated, to
the state that it becomes difficult to see what was the fundamental
reason for its existence in the first place. I would guess, that Hirth,
being a practical engineer, just made it in the workshop, then decided
to document it afterwards, most likely quicker than calculating angles,
etc., back then.
I think, as soon as you change the design so that the matching parts are
not identical, or do not have straight and flat flanks to the ridges,
then it is no longer a Hirth coupling.
On 17/11/2024 18:46, Adrian Mariano wrote:
> Ray, I have to say that I've found the complexity lurking in this
> hirth joint to be kind of baffling. When I saw Bob's first attempt I
> immediately thought Bob was massively overcomplicating things. But I
> was wrong. It seems like it should be very simple, and yet it seems
> to be remarkably subtle and complicated. We're not "making" it that
> way---that's just the way it is. I thought it was trivial and wrote a
> straight forward code and then found that it didn't work in various
> cases---it was wrong, in other words, and getting it right is hard.
> Or at least I didn't find an easy way to get it right, and neither did
> Bob. And when I say it was wrong, I mean that the joint didn't mate
> properly. Clearly something different happens if you approach the
> design with "I have a 60 deg milling cutter, how do I cut a 100 tooth
> hirth joint" than "I want to construct a mathematical model that makes
> a generic version of this joint". I think another factor is that a
> lot of the subtlety results in errors that become small when there are
> lots of teeth. I see potential interesting applications for this
> joint with small numbers of teeth like perhaps 8 or 4 to create
> mechanisms that lock into a small number of positions, so I don't want
> to ignore those small tooth count cases.
>
> Regarding tooth angle, I attempted to measure it at the tooth ridge
> with nominal tooth angle set to 60 and zero cone angle. With four
> teeth I get 76.8 deg instead of 60 deg. With 44 teeth I get 60.16
> deg. With 144 teeth it's 60.01 deg. If I raise the cone angle to 30
> deg then I actually get 60.4 in the 4 tooth case, but in the 44 tooth
> case it's now 65.5 deg and with 144 teeth it's 66.8 deg. Why does
> the 30 deg cone angle make the 4 tooth case so close to the nominal
> angle? It's because the tooth ridge in this case is very close to
> parallel to the xy plane, which matches the design angle reference for
> the construction of the triangle. Here's a picture (4 teeth, 30 deg
> cone angle, 60 deg nominal tooth angle):
>
> image.png
>
> So it seems like the deviation of tooth angle for small tooth count
> has to do with fitting the teeth around a circle. When you have lots
> of teeth, it's approximately like fitting the teeth onto a line and
> nothing weird happens, but when you curve just 4 teeth around a
> circle, the angles no longer add up as expected for flat geometry,
> resulting in an alteration of the actual realized tooth angle. So to
> produce teeth that match the nominal angle there are two corrections
> needed. One is a correction for fitting a linear arrangement of
> triangles around a circle, with increasing correction as the number of
> teeth shrinks. The other one has to do with cone angle, and at least
> for my definition of cone angle, the correction looks like it gets
> smaller and then larger again as you increase the cone angle---at
> least for the small tooth count case.
>
> On Sun, Nov 17, 2024 at 12:44 PM Raymond West via Discuss
> <discuss@lists.openscad.org> wrote:
>
> Afaik, The Hirth joint was invented in 1928, and was very simple
> to manufacture, with the machinery available at the time. I'm
> pretty sure, that none of the detail On Hirth Ring Couplings:
> Design Principles Including the Effect of Friction
> <https://www.mdpi.com/2076-0825/7/4/79> for example, was known.
> I'm not sure why it is being made so complicated on here.
>
> On 17/11/2024 13:22, Michael Möller via Discuss wrote:
>>
>>
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Sun, Nov 17, 2024 9:44 PM
Ray, so if I understand your description, you have the blank you're
grinding mounted at an angle and you then use your 60 deg grinding wheel to
grind the groove, which due to the angled mount, tapers from full depth at
the edge to zero depth in the center. Is that right? If the answer is
yes, then it appears to me that the result is NOT a 60 deg angle on the
teeth, because the cutter meets the workpiece at an angle, the effective
tooth angle is modified by that angle at which the blank is tilted.
I also found that to get a symmetric self-mating joint I had to "grind" at
half that angle, in effect. That is, I had to make the centerline of the
teeth intersect each other at the origin, not the teeth tips or the teeth
valleys. I tried it the other way at first and it didn't work.
On Sun, Nov 17, 2024 at 4:15 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
Hi Adrian,
The code I sent seemed to be OK for anything more than two teeth. Maybe if
I explain how I think it would have been originally made will let you see
where you are getting odd angles. The first requirement would be a grinding
wheel. (I would guess that it was most likely a milling cutter, and
material brass, but never mind, same principle.) The standard angles for
such discs would either be 90 degree or 60 degree (inclusive angle), others
would most likely be more expensive. This would be a disc, with a v edge
(at 90 or 60 degrees). The edge of the disc would be rounded, since a
pointed edge would not last long. This would be used in a horizontal
grinder, the disc can be raised or lowered, and the bed traversed
backwards and forwards under the wheel. A piece of steel, fixed to the bed
could thus have a v groove ground into it, and the profile, if no sideways
movement, would be the inverse of the grinding disk, it would have a
rounded bottom (fillet) to the groove.
Now, if you have a rotary table, then you can clamp a round piece of steel
to that, and rotate the table a certain part of a revolution. So, say, move
in 30 degree steps, and you will get 6 v grooves, crossing in the centre of
the stock piece (or 12 meeting at the centre...) as you traverse the piece
at the fixed angle beneath the grinding disc.
Now, wedge up one end of the rotary table. A new piece of stock will give
you 12 v grooves, say, but shallower towards the centre. If you make it,
such that the grooves are at zero depth at the centre, and full depth at
the edge, and there are the correct number of grooves, then two such
pieces will mesh together, and tend to self centre. Of course, the bottom
of grooves are filleted due to the shape of the grinding wheel. The fillet
will be a constant width. To get two such pieces to fit together, the peaks
need to be rounded over, but flattening them is simpler, and in some ways
better (else the point of the mating ridge bottoms out on the fillet). The
centres of the round stock pieces can be machined away, since there is
little force transmitted there, and for other reasons. So, simple
calculations can be made, depending on the tooling available, size of
desired coupling joint and number of teeth, etc.
Say we have a work piece diameter 40, and a grinding disc, say, width 8,
and 90 degree angle. We can calculate the minimum number of teeth from d=40
and chord = 8. The maximum will depend on the radius of the 90 degree edge
of the grinding wheel (which creates the fillet - we don't want all
fillet!), but let's say 50. That means the rotary table increments must be
in steps of 360/50 =7.2 degrees. If we were going full depth of cut, then
the maximum depth would be 4 (angle of 90 degrees), and 8 between peaks
(but we can't go full depth at 7.2degrees).
So, given the length of chord, and diameter of work, we can find the
number of chords, n, from d=(chord/ (sin(180/n))) we can solve that for
chord, and then the height of the ridge will be half of the chord length
(90 degree angle to wheel)- the assumption is that the grinding wheel edge
is pointed, not rounded.
Now, we want the grinding wheel to cut the depth calculated at the edge of
the work piece, but just touch the centre of the workpiece, so we can
calculate that we need to fix it at an angle that is
ASIN(ridge_height/2)/diam).
That will give a self centring matching Hirth joints, which afaik complies
with the 1928 original specification.
For the purposes of calculation ignore the radius at the bottom of the
grooves - that will depend on the wheel profile. As to all intents and
purposes, the bottom of the fillet will be parallel to the bottom of the
estimated groove, so the angle to the horizontal will be the same. The top
of the flattened ridge can be wider than the width of the fillet, but the
edges of the flat will be parallel, too.
Like most things, it starts off simple, then gets overcomplicated, to the
state that it becomes difficult to see what was the fundamental reason for
its existence in the first place. I would guess, that Hirth, being a
practical engineer, just made it in the workshop, then decided to document
it afterwards, most likely quicker than calculating angles, etc., back
then.
I think, as soon as you change the design so that the matching parts are
not identical, or do not have straight and flat flanks to the ridges, then
it is no longer a Hirth coupling.
On 17/11/2024 18:46, Adrian Mariano wrote:
Ray, I have to say that I've found the complexity lurking in this hirth
joint to be kind of baffling. When I saw Bob's first attempt I
immediately thought Bob was massively overcomplicating things. But I was
wrong. It seems like it should be very simple, and yet it seems to be
remarkably subtle and complicated. We're not "making" it that
way---that's just the way it is. I thought it was trivial and wrote a
straight forward code and then found that it didn't work in various
cases---it was wrong, in other words, and getting it right is hard. Or at
least I didn't find an easy way to get it right, and neither did Bob. And
when I say it was wrong, I mean that the joint didn't mate properly.
Clearly something different happens if you approach the design with "I have
a 60 deg milling cutter, how do I cut a 100 tooth hirth joint" than "I want
to construct a mathematical model that makes a generic version of this
joint". I think another factor is that a lot of the subtlety results in
errors that become small when there are lots of teeth. I see potential
interesting applications for this joint with small numbers of teeth like
perhaps 8 or 4 to create mechanisms that lock into a small number of
positions, so I don't want to ignore those small tooth count cases.
Regarding tooth angle, I attempted to measure it at the tooth ridge with
nominal tooth angle set to 60 and zero cone angle. With four teeth I get
76.8 deg instead of 60 deg. With 44 teeth I get 60.16 deg. With 144 teeth
it's 60.01 deg. If I raise the cone angle to 30 deg then I actually get
60.4 in the 4 tooth case, but in the 44 tooth case it's now 65.5 deg and
with 144 teeth it's 66.8 deg. Why does the 30 deg cone angle make the 4
tooth case so close to the nominal angle? It's because the tooth ridge in
this case is very close to parallel to the xy plane, which matches the
design angle reference for the construction of the triangle. Here's a
picture (4 teeth, 30 deg cone angle, 60 deg nominal tooth angle):
[image: image.png]
So it seems like the deviation of tooth angle for small tooth count has to
do with fitting the teeth around a circle. When you have lots of teeth,
it's approximately like fitting the teeth onto a line and nothing weird
happens, but when you curve just 4 teeth around a circle, the angles no
longer add up as expected for flat geometry, resulting in an alteration of
the actual realized tooth angle. So to produce teeth that match the
nominal angle there are two corrections needed. One is a correction for
fitting a linear arrangement of triangles around a circle, with increasing
correction as the number of teeth shrinks. The other one has to do with
cone angle, and at least for my definition of cone angle, the correction
looks like it gets smaller and then larger again as you increase the cone
angle---at least for the small tooth count case.
On Sun, Nov 17, 2024 at 12:44 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
Afaik, The Hirth joint was invented in 1928, and was very simple to
manufacture, with the machinery available at the time. I'm pretty sure,
that none of the detail On Hirth Ring Couplings: Design Principles
Including the Effect of Friction https://www.mdpi.com/2076-0825/7/4/79
for example, was known. I'm not sure why it is being made so complicated on
here.
On 17/11/2024 13:22, Michael Möller via Discuss wrote:
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Ray, so if I understand your description, you have the blank you're
grinding mounted at an angle and you then use your 60 deg grinding wheel to
grind the groove, which due to the angled mount, tapers from full depth at
the edge to zero depth in the center. Is that right? If the answer is
yes, then it appears to me that the result is NOT a 60 deg angle on the
teeth, because the cutter meets the workpiece at an angle, the effective
tooth angle is modified by that angle at which the blank is tilted.
I also found that to get a symmetric self-mating joint I had to "grind" at
half that angle, in effect. That is, I had to make the centerline of the
teeth intersect each other at the origin, not the teeth tips or the teeth
valleys. I tried it the other way at first and it didn't work.
On Sun, Nov 17, 2024 at 4:15 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
> Hi Adrian,
>
> The code I sent seemed to be OK for anything more than two teeth. Maybe if
> I explain how I think it would have been originally made will let you see
> where you are getting odd angles. The first requirement would be a grinding
> wheel. (I would guess that it was most likely a milling cutter, and
> material brass, but never mind, same principle.) The standard angles for
> such discs would either be 90 degree or 60 degree (inclusive angle), others
> would most likely be more expensive. This would be a disc, with a v edge
> (at 90 or 60 degrees). The edge of the disc would be rounded, since a
> pointed edge would not last long. This would be used in a horizontal
> grinder, the disc can be raised or lowered, and the bed traversed
> backwards and forwards under the wheel. A piece of steel, fixed to the bed
> could thus have a v groove ground into it, and the profile, if no sideways
> movement, would be the inverse of the grinding disk, it would have a
> rounded bottom (fillet) to the groove.
>
> Now, if you have a rotary table, then you can clamp a round piece of steel
> to that, and rotate the table a certain part of a revolution. So, say, move
> in 30 degree steps, and you will get 6 v grooves, crossing in the centre of
> the stock piece (or 12 meeting at the centre...) as you traverse the piece
> at the fixed angle beneath the grinding disc.
>
> Now, wedge up one end of the rotary table. A new piece of stock will give
> you 12 v grooves, say, but shallower towards the centre. If you make it,
> such that the grooves are at zero depth at the centre, and full depth at
> the edge, and there are the correct number of grooves, then two such
> pieces will mesh together, and tend to self centre. Of course, the bottom
> of grooves are filleted due to the shape of the grinding wheel. The fillet
> will be a constant width. To get two such pieces to fit together, the peaks
> need to be rounded over, but flattening them is simpler, and in some ways
> better (else the point of the mating ridge bottoms out on the fillet). The
> centres of the round stock pieces can be machined away, since there is
> little force transmitted there, and for other reasons. So, simple
> calculations can be made, depending on the tooling available, size of
> desired coupling joint and number of teeth, etc.
>
> Say we have a work piece diameter 40, and a grinding disc, say, width 8,
> and 90 degree angle. We can calculate the minimum number of teeth from d=40
> and chord = 8. The maximum will depend on the radius of the 90 degree edge
> of the grinding wheel (which creates the fillet - we don't want all
> fillet!), but let's say 50. That means the rotary table increments must be
> in steps of 360/50 =7.2 degrees. If we were going full depth of cut, then
> the maximum depth would be 4 (angle of 90 degrees), and 8 between peaks
> (but we can't go full depth at 7.2degrees).
>
> So, given the length of chord, and diameter of work, we can find the
> number of chords, n, from d=(chord/ (sin(180/n))) we can solve that for
> chord, and then the height of the ridge will be half of the chord length
> (90 degree angle to wheel)- the assumption is that the grinding wheel edge
> is pointed, not rounded.
>
> Now, we want the grinding wheel to cut the depth calculated at the edge of
> the work piece, but just touch the centre of the workpiece, so we can
> calculate that we need to fix it at an angle that is
> ASIN(ridge_height/2)/diam).
>
> That will give a self centring matching Hirth joints, which afaik complies
> with the 1928 original specification.
>
> For the purposes of calculation ignore the radius at the bottom of the
> grooves - that will depend on the wheel profile. As to all intents and
> purposes, the bottom of the fillet will be parallel to the bottom of the
> estimated groove, so the angle to the horizontal will be the same. The top
> of the flattened ridge can be wider than the width of the fillet, but the
> edges of the flat will be parallel, too.
>
> Like most things, it starts off simple, then gets overcomplicated, to the
> state that it becomes difficult to see what was the fundamental reason for
> its existence in the first place. I would guess, that Hirth, being a
> practical engineer, just made it in the workshop, then decided to document
> it afterwards, most likely quicker than calculating angles, etc., back
> then.
>
> I think, as soon as you change the design so that the matching parts are
> not identical, or do not have straight and flat flanks to the ridges, then
> it is no longer a Hirth coupling.
>
>
> On 17/11/2024 18:46, Adrian Mariano wrote:
>
> Ray, I have to say that I've found the complexity lurking in this hirth
> joint to be kind of baffling. When I saw Bob's first attempt I
> immediately thought Bob was massively overcomplicating things. But I was
> wrong. It seems like it should be very simple, and yet it seems to be
> remarkably subtle and complicated. We're not "making" it that
> way---that's just the way it is. I thought it was trivial and wrote a
> straight forward code and then found that it didn't work in various
> cases---it was wrong, in other words, and getting it right is hard. Or at
> least I didn't find an easy way to get it right, and neither did Bob. And
> when I say it was wrong, I mean that the joint didn't mate properly.
> Clearly something different happens if you approach the design with "I have
> a 60 deg milling cutter, how do I cut a 100 tooth hirth joint" than "I want
> to construct a mathematical model that makes a generic version of this
> joint". I think another factor is that a lot of the subtlety results in
> errors that become small when there are lots of teeth. I see potential
> interesting applications for this joint with small numbers of teeth like
> perhaps 8 or 4 to create mechanisms that lock into a small number of
> positions, so I don't want to ignore those small tooth count cases.
>
> Regarding tooth angle, I attempted to measure it at the tooth ridge with
> nominal tooth angle set to 60 and zero cone angle. With four teeth I get
> 76.8 deg instead of 60 deg. With 44 teeth I get 60.16 deg. With 144 teeth
> it's 60.01 deg. If I raise the cone angle to 30 deg then I actually get
> 60.4 in the 4 tooth case, but in the 44 tooth case it's now 65.5 deg and
> with 144 teeth it's 66.8 deg. Why does the 30 deg cone angle make the 4
> tooth case so close to the nominal angle? It's because the tooth ridge in
> this case is very close to parallel to the xy plane, which matches the
> design angle reference for the construction of the triangle. Here's a
> picture (4 teeth, 30 deg cone angle, 60 deg nominal tooth angle):
>
> [image: image.png]
>
> So it seems like the deviation of tooth angle for small tooth count has to
> do with fitting the teeth around a circle. When you have lots of teeth,
> it's approximately like fitting the teeth onto a line and nothing weird
> happens, but when you curve just 4 teeth around a circle, the angles no
> longer add up as expected for flat geometry, resulting in an alteration of
> the actual realized tooth angle. So to produce teeth that match the
> nominal angle there are two corrections needed. One is a correction for
> fitting a linear arrangement of triangles around a circle, with increasing
> correction as the number of teeth shrinks. The other one has to do with
> cone angle, and at least for my definition of cone angle, the correction
> looks like it gets smaller and then larger again as you increase the cone
> angle---at least for the small tooth count case.
>
> On Sun, Nov 17, 2024 at 12:44 PM Raymond West via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> Afaik, The Hirth joint was invented in 1928, and was very simple to
>> manufacture, with the machinery available at the time. I'm pretty sure,
>> that none of the detail On Hirth Ring Couplings: Design Principles
>> Including the Effect of Friction <https://www.mdpi.com/2076-0825/7/4/79>
>> for example, was known. I'm not sure why it is being made so complicated on
>> here.
>>
>> On 17/11/2024 13:22, Michael Möller via Discuss wrote:
>>
>>
>>
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

M
mikeonenine@web.de
Sun, Nov 17, 2024 11:47 PM
Ray, so if I understand your description, you have the blank you're
grinding mounted at an angle and you then use your 60 deg grinding wheel to
grind the groove, which due to the angled mount, tapers from full depth at
the edge to zero depth in the center. Is that right? If the answer is
yes, then it appears to me that the result is NOT a 60 deg angle on the
teeth, because the cutter meets the workpiece at an angle, the effective
tooth angle is modified by that angle at which the blank is tilted.
That seems to confirm my hunch and it makes sense as then only 60° and 90° tools are required instead of a whole range of different custom-made tools. The resulting splines are then only nominally 60° or 90° while the groove is precisely that angle. Can this be expected to give a proper fit?
The problem for us is also that CAD/3D printing and the machining process work on different principles.
For a little extra complication: what does “fit” mean? To me it means that the flanks must be in contact over the whole area. Even 0.01 mm of clearance means no contact, and no transmission of forces, so that these are concentrated on a small area. It can be seen most clearly in joints with a small number of splines whether full contact is achieved, or not.
However, the discrepancy decreases rapidly with increasing numbers of splines, and even further if the ring of splines is narrow, so that at some point it will become negligible.
I also found that to get a symmetric self-mating joint I had to "grind" at
half that angle, in effect. That is, I had to make the centerline of the
teeth intersect each other at the origin, not the teeth tips or the teeth
valleys. I tried it the other way at first and it didn't work.
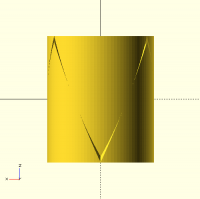
I would confirm that, the centreline being at half spline height. But with 3 splines, they only touch in the middle - see screenshot of joint with 90° splines (included angle around the ridge, flank to flank).
BTW Hirth couplings were not at all simple to manufacture, with the machinery available at the time and were a luxury. A crankshaft with Hirth couplings for a Grand Prix racing car cost as much as a house.
Adrian Mariano wrote:
> Ray, so if I understand your description, you have the blank you're
> grinding mounted at an angle and you then use your 60 deg grinding wheel to
> grind the groove, which due to the angled mount, tapers from full depth at
> the edge to zero depth in the center. Is that right? If the answer is
> yes, then it appears to me that the result is NOT a 60 deg angle on the
> teeth, because the cutter meets the workpiece at an angle, the effective
> tooth angle is modified by that angle at which the blank is tilted.
That seems to confirm my hunch and it makes sense as then only 60° and 90° tools are required instead of a whole range of different custom-made tools. The resulting splines are then only nominally 60° or 90° while the groove is precisely that angle. Can this be expected to give a proper fit?
The problem for us is also that CAD/3D printing and the machining process work on different principles.
For a little extra complication: what does “fit” mean? To me it means that the flanks must be in contact over the whole area. Even 0.01 mm of clearance means no contact, and no transmission of forces, so that these are concentrated on a small area. It can be seen most clearly in joints with a small number of splines whether full contact is achieved, or not.
However, the discrepancy decreases rapidly with increasing numbers of splines, and even further if the ring of splines is narrow, so that at some point it will become negligible.
> I also found that to get a symmetric self-mating joint I had to "grind" at \
> half that angle, in effect. That is, I had to make the centerline of the \
> teeth intersect each other at the origin, not the teeth tips or the teeth \
> valleys. I tried it the other way at first and it didn't work.
I would confirm that, the centreline being at half spline height. But with 3 splines, they only touch in the middle - see screenshot of joint with 90° splines (included angle around the ridge, flank to flank).
BTW Hirth couplings were not at all simple to manufacture, with the machinery available at the time and were a luxury. A crankshaft with Hirth couplings for a Grand Prix racing car cost as much as a house.

AM
Adrian Mariano
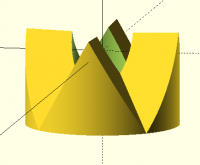
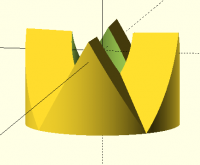
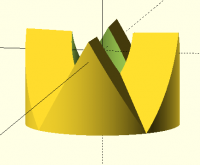
Mon, Nov 18, 2024 12:16 AM
I'm not sure what you mean about "with 3 splines they only touch in the
middle". That's only true if the model is wrong, like so many of my early
attempts. With a correct model this is not the case, of course. What
model gave you the behavior in question? Or do you mean the model
constructed as described by Ray? It may be the case that an improper fit
was good enough for machinists making these joints with lots of teeth? For
my current code I get the image below, where I separated the parts by a
tiny amount to show the gap. I'm pretty sure Bob's model also gives the
same result, namely that parts mate exactly along the entire joint
surface. Our models are designed mathematically to ensure that they mate
exactly. I realized that I never really examined Ray's model because I
couldn't get it to render in either OpenSCAD I had (not the stable nor the
dev) and preview was unusably slow on my machine.
[image: image.png]
On Sun, Nov 17, 2024 at 6:47 PM Caddiy via Discuss <
discuss@lists.openscad.org> wrote:
Adrian Mariano wrote:
Ray, so if I understand your description, you have the blank you're
grinding mounted at an angle and you then use your 60 deg grinding wheel to
grind the groove, which due to the angled mount, tapers from full depth at
the edge to zero depth in the center. Is that right? If the answer is yes,
then it appears to me that the result is NOT a 60 deg angle on the teeth,
because the cutter meets the workpiece at an angle, the effective tooth
angle is modified by that angle at which the blank is tilted.
That seems to confirm my hunch and it makes sense as then only 60° and 90°
tools are required instead of a whole range of different custom-made tools.
The resulting splines are then only nominally 60° or 90° while the groove
is precisely that angle. Can this be expected to give a proper fit?
The problem for us is also that CAD/3D printing and the machining process
work on different principles.
For a little extra complication: what does “fit” mean? To me it means that
the flanks must be in contact over the whole area. Even 0.01 mm of
clearance means no contact, and no transmission of forces, so that these
are concentrated on a small area. It can be seen most clearly in joints
with a small number of splines whether full contact is achieved, or not.
However, the discrepancy decreases rapidly with increasing numbers of
splines, and even further if the ring of splines is narrow, so that at some
point it will become negligible.
I also found that to get a symmetric self-mating joint I had to "grind" at
half that angle, in effect. That is, I had to make the centerline of the
teeth intersect each other at the origin, not the teeth tips or the teeth
valleys. I tried it the other way at first and it didn't work.
I would confirm that, the centreline being at half spline height. But with
3 splines, they only touch in the middle - see screenshot of joint with 90°
splines (included angle around the ridge, flank to flank).
BTW Hirth couplings were not at all simple to manufacture, with the
machinery available at the time and were a luxury. A crankshaft with Hirth
couplings for a Grand Prix racing car cost as much as a house.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I'm not sure what you mean about "with 3 splines they only touch in the
middle". That's only true if the model is wrong, like so many of my early
attempts. With a correct model this is not the case, of course. What
model gave you the behavior in question? Or do you mean the model
constructed as described by Ray? It may be the case that an improper fit
was good enough for machinists making these joints with lots of teeth? For
my current code I get the image below, where I separated the parts by a
tiny amount to show the gap. I'm pretty sure Bob's model also gives the
same result, namely that parts mate exactly along the entire joint
surface. Our models are designed mathematically to ensure that they mate
exactly. I realized that I never really examined Ray's model because I
couldn't get it to render in either OpenSCAD I had (not the stable nor the
dev) and preview was unusably slow on my machine.
[image: image.png]
On Sun, Nov 17, 2024 at 6:47 PM Caddiy via Discuss <
discuss@lists.openscad.org> wrote:
> Adrian Mariano wrote:
>
> Ray, so if I understand your description, you have the blank you're
> grinding mounted at an angle and you then use your 60 deg grinding wheel to
> grind the groove, which due to the angled mount, tapers from full depth at
> the edge to zero depth in the center. Is that right? If the answer is yes,
> then it appears to me that the result is NOT a 60 deg angle on the teeth,
> because the cutter meets the workpiece at an angle, the effective tooth
> angle is modified by that angle at which the blank is tilted.
>
> That seems to confirm my hunch and it makes sense as then only 60° and 90°
> tools are required instead of a whole range of different custom-made tools.
> The resulting splines are then only nominally 60° or 90° while the groove
> is precisely that angle. Can this be expected to give a proper fit?
>
> The problem for us is also that CAD/3D printing and the machining process
> work on different principles.
>
> For a little extra complication: what does “fit” mean? To me it means that
> the flanks must be in contact over the whole area. Even 0.01 mm of
> clearance means no contact, and no transmission of forces, so that these
> are concentrated on a small area. It can be seen most clearly in joints
> with a small number of splines whether full contact is achieved, or not.
>
> However, the discrepancy decreases rapidly with increasing numbers of
> splines, and even further if the ring of splines is narrow, so that at some
> point it will become negligible.
>
> I also found that to get a symmetric self-mating joint I had to "grind" at
> half that angle, in effect. That is, I had to make the centerline of the
> teeth intersect each other at the origin, not the teeth tips or the teeth
> valleys. I tried it the other way at first and it didn't work.
>
> I would confirm that, the centreline being at half spline height. But with
> 3 splines, they only touch in the middle - see screenshot of joint with 90°
> splines (included angle around the ridge, flank to flank).
>
> BTW Hirth couplings were not at all simple to manufacture, with the
> machinery available at the time and were a luxury. A crankshaft with Hirth
> couplings for a Grand Prix racing car cost as much as a house.
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>