AM
Adrian Mariano
Thu, Nov 7, 2024 11:09 AM
I do not understand the pictures. Or at least the top one is mystifying.
The bottom one looks like it could describe the process: the projection is
along vectors that originate at the origin and yes, you have a separate
projection onto the inner and outer cylinder.
On Wed, Nov 6, 2024 at 11:24 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
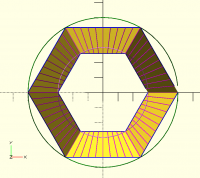
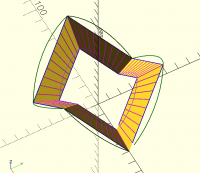
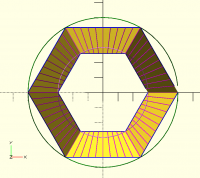
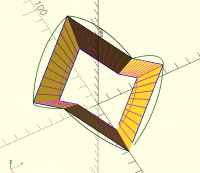
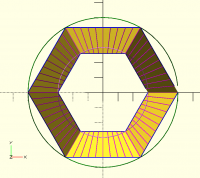
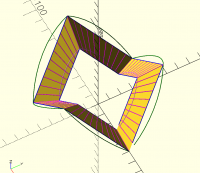
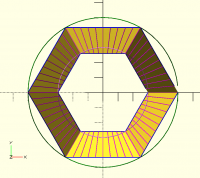
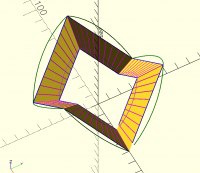
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) &&
tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
",360*(n-1)/2/n," for spline with ",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define both
chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value") ;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized tooth
height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going around
the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2),
valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts, reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
col_wrap=true, row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the
theta for the chamfer “shoulder” point would be proportional to the chamfer
but it produces a slight error. It is barely noticeable but gets more
blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I do not understand the pictures. Or at least the top one is mystifying.
The bottom one looks like it could describe the process: the projection is
along vectors that originate at the origin and yes, you have a separate
projection onto the inner and outer cylinder.
On Wed, Nov 6, 2024 at 11:24 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I don't think the straight projection on cylinder will work.
> The only way I think this can work is if you project using vectors
> considering outer race and inner race, projecting outwards and inwards
> respectively on outer and inner cylinder.
> picture below can make this clear.
> magenta lines are the vectors
> [image: Screenshot 2024-11-07 at 9.49.27 AM.png]
> [image: Screenshot 2024-11-07 at 9.53.29 AM.png]
>
> On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
> discuss@lists.openscad.org> wrote:
>
>> Bob, I did I think exactly the same thing in my code and didn't notice
>> anything, but now that you mention it, doing chamfers on an angular basis
>> is of course not going to match doing them on a linear basis. So that
>> means the geometry changes a bit if you change the chamfer size. This
>> isn't necessarily catastrophic, but is a little unexpected, I suppose.
>> Generally speaking you can't mate two parts produced with different chamfer
>> size anyway, so I'm not sure this is crucial to get right. But in order to
>> get it right, I think both thetaCA2 and phiCA are going to need to be
>> computed with trig---either that or there's some complicated way of
>> computing just one. The question is whether these two parameters can be
>> computed independently or are they related in some complicated way.
>> Treated as a 2d problem you are trying to get the angle that corresponds to
>> a fraction of a chord of the circle, which is a reasonably straight forward
>> triangle calculation. I got atan(chamfer*tan(angle)) where angle is
>> 180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
>> align with the unchamfered. For example:
>>
>> [image: image.png]
>>
>> Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
>> slightly larger radius so we can see it clearly). And we see that the
>> angle has changed. I actually got less error with the original
>> calculation, but that might be because I didn't correct the phi angle only
>> the theta angle. (Or maybe I botched the trig.) So I tried computing a
>> correction for phi and got ridge_angle-atan(ridge_angle -
>> chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
>> up correctly. (And the horizontal correction is still worse than not,
>> which makes me wonder if the horizontal correction needs to take into
>> account the vertical position of the chamfer somehow.) Doing the phi
>> correction alone actually is an improvement over no correction.
>>
>> Here's my current code (without any chamfer corrections). It does
>> rounding and skew teeth.
>>
>> module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
>> rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
>> {
>> ir = get_radius(r=ir,d=id);
>> or = get_radius(r=or,d=od);
>> dummy = assert(all_positive([ir]), "ir/id must be a positive value")
>> assert(all_positive([or]), "or/od must be a positive value")
>> assert(is_int(n) && n>1, "n must be an integer larger than 1")
>> assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
>> between -1 and 1")
>> assert(ir<or, "inside radius (ir/id) must be smaller than
>> outside radius (or/od)")
>> assert(all_positive([tooth_angle]) &&
>> tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
>> ",360*(n-1)/2/n," for spline with ",n," teeth."))
>> assert(num_defined([chamfer,rounding]) <=1, "Cannot define both
>> chamfer and rounding")
>> assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
>> chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
>> assert(is_undef(rounding) || all_nonnegative([rounding]) &&
>> rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
>> assert(all_positive([base]), "base must be a positive value") ;
>> tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized tooth
>> height
>> cone_height = -tan(cone_angle); // Normalized
>> height change corresponding to the cone angle
>> ridge_angle = atan(tooth_height/2 + cone_height);
>> valley_angle = atan(-tooth_height/2 + cone_height);
>> angle = 180/n; // Half the angle occupied by each tooth going around
>> the circle
>>
>> factor = crop ? 3 : 1; // Make it oversized when crop is true
>>
>> profile = is_undef(rounding) || rounding==0 ?
>> let(
>> chamfer=default(chamfer,0),
>> vchamf = chamfer*(ridge_angle-valley_angle),
>> pts = [
>> [-angle*(1-chamfer/2),
>> valley_angle+vchamf/2],
>> [-angle*chamfer, ridge_angle-vchamf]
>> ],
>> full = deduplicate(concat(pts, reverse(xflip(pts))))
>> )
>> back(valley_angle,
>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
>> : let(
>> vround=rounding*(ridge_angle-valley_angle),
>> profpts = [
>> [ -angle, valley_angle+vround/2],
>> [ -angle*(1-rounding/2),
>> valley_angle+vround/2],
>> [ -angle*rounding, ridge_angle-vround],
>> ],
>> segs = max(16,segs(or*rounding)),
>> full = concat(profpts, reverse(xflip(profpts))),
>> skewed = back(valley_angle,
>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
>> // Using computed values for the joints
>> lead to round-off error issues
>> joints = [(skewed[1]-skewed[0]).x,
>> (skewed[3]-skewed[2]).x/2,
>> (skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
>> roundpts = round_corners(skewed, joint=joints,
>> closed=false,$fn=segs)
>> )
>> roundpts;
>>
>> // project spherical coordinate point onto cylinder of radius r
>> cyl_proj = function (r,theta_phi)
>> [for(pt=theta_phi)
>> let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
>> r * xyz / norm(point2d(xyz))];
>>
>> bottom =
>> min([tan(valley_angle)*ir,tan(valley_angle)*or])-base-cone_height*ir;
>> safebottom =
>> min([tan(valley_angle)*ir/factor,tan(valley_angle)*or*factor])-base-(crop?1:0)-cone_height*ir;
>> ang_ofs = !rot ? -skew*angle
>> : n%2==0 ? -(angle-skew*angle) - skew*angle
>> : -angle*(2-skew)-skew*angle;
>> topinner = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>> each
>> zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
>> topouter = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>> each
>> zrot(ang+ang_ofs,cyl_proj(factor*or,profile))]);
>> botinner = [for(val=topinner) [val.x,val.y,safebottom]];
>> botouter = [for(val=topouter) [val.x,val.y,safebottom]];
>> vert = [topouter, topinner, botinner, botouter];
>>
>> anchors = [
>> named_anchor("teeth_bot", [0,0,bottom], DOWN)
>> ];
>> attachable(anchor=anchor,spin=spin,orient=orient, r=or,
>> h=-2*bottom,anchors=anchors){
>> intersection(){
>> vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
>> col_wrap=true, row_wrap=true),convexity=min(10,n));
>> if (crop)
>>
>> zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
>> }
>> children();
>> }
>> }
>>
>>
>>
>> On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>>> I have established that there is an error in the code fragment. The line
>>>
>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>
>>> Is where the error lies. What should it be? I was assuming that the
>>> theta for the chamfer “shoulder” point would be proportional to the chamfer
>>> but it produces a slight error. It is barely noticeable but gets more
>>> blatant at low tooth counts and high conic.
>>>
>>> Anyone see what it should be? I’m guessing there is some trig
>>> functions involved,but ...
>>>
>>> -Bob
>>>
>>> On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
>>> discuss@lists.openscad.org> wrote:
>>>
>>> Here is just a code fragment but it gets the point across.
>>>
>>> IR = _ir(hs);
>>> OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
>>> circumscribing polygon of N
>>>
>>> // Ridge Chamfer
>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>> phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
>>>
>>> function profileToooth(r) =
>>> [spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
>>> phiCA),
>>> spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
>>> spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
>>> spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
>>> phiCA)
>>> ];
>>>
>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
>

SP
Sanjeev Prabhakar
Thu, Nov 7, 2024 11:23 AM
All the magenta lines are vectors, you can think of them originating from
any side of the line.
Each line intersects a circumscribing cylinder outer or inner and that
forms the circular hirth coupling.
On Thu, 7 Nov, 2024, 4:40 pm Adrian Mariano, avm4@cornell.edu wrote:
I do not understand the pictures. Or at least the top one is mystifying.
The bottom one looks like it could describe the process: the projection is
along vectors that originate at the origin and yes, you have a separate
projection onto the inner and outer cylinder.
On Wed, Nov 6, 2024 at 11:24 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) &&
tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
",360*(n-1)/2/n," for spline with ",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define
both chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value") ;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
tooth height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going
around the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2),
valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts, reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
col_wrap=true, row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the
theta for the chamfer “shoulder” point would be proportional to the chamfer
but it produces a slight error. It is barely noticeable but gets more
blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
All the magenta lines are vectors, you can think of them originating from
any side of the line.
Each line intersects a circumscribing cylinder outer or inner and that
forms the circular hirth coupling.
On Thu, 7 Nov, 2024, 4:40 pm Adrian Mariano, <avm4@cornell.edu> wrote:
> I do not understand the pictures. Or at least the top one is mystifying.
> The bottom one looks like it could describe the process: the projection is
> along vectors that originate at the origin and yes, you have a separate
> projection onto the inner and outer cylinder.
>
> On Wed, Nov 6, 2024 at 11:24 PM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> I don't think the straight projection on cylinder will work.
>> The only way I think this can work is if you project using vectors
>> considering outer race and inner race, projecting outwards and inwards
>> respectively on outer and inner cylinder.
>> picture below can make this clear.
>> magenta lines are the vectors
>> [image: Screenshot 2024-11-07 at 9.49.27 AM.png]
>> [image: Screenshot 2024-11-07 at 9.53.29 AM.png]
>>
>> On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
>> discuss@lists.openscad.org> wrote:
>>
>>> Bob, I did I think exactly the same thing in my code and didn't notice
>>> anything, but now that you mention it, doing chamfers on an angular basis
>>> is of course not going to match doing them on a linear basis. So that
>>> means the geometry changes a bit if you change the chamfer size. This
>>> isn't necessarily catastrophic, but is a little unexpected, I suppose.
>>> Generally speaking you can't mate two parts produced with different chamfer
>>> size anyway, so I'm not sure this is crucial to get right. But in order to
>>> get it right, I think both thetaCA2 and phiCA are going to need to be
>>> computed with trig---either that or there's some complicated way of
>>> computing just one. The question is whether these two parameters can be
>>> computed independently or are they related in some complicated way.
>>> Treated as a 2d problem you are trying to get the angle that corresponds to
>>> a fraction of a chord of the circle, which is a reasonably straight forward
>>> triangle calculation. I got atan(chamfer*tan(angle)) where angle is
>>> 180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
>>> align with the unchamfered. For example:
>>>
>>> [image: image.png]
>>>
>>> Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
>>> slightly larger radius so we can see it clearly). And we see that the
>>> angle has changed. I actually got less error with the original
>>> calculation, but that might be because I didn't correct the phi angle only
>>> the theta angle. (Or maybe I botched the trig.) So I tried computing a
>>> correction for phi and got ridge_angle-atan(ridge_angle -
>>> chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
>>> up correctly. (And the horizontal correction is still worse than not,
>>> which makes me wonder if the horizontal correction needs to take into
>>> account the vertical position of the chamfer somehow.) Doing the phi
>>> correction alone actually is an improvement over no correction.
>>>
>>> Here's my current code (without any chamfer corrections). It does
>>> rounding and skew teeth.
>>>
>>> module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
>>> rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
>>> {
>>> ir = get_radius(r=ir,d=id);
>>> or = get_radius(r=or,d=od);
>>> dummy = assert(all_positive([ir]), "ir/id must be a positive value")
>>> assert(all_positive([or]), "or/od must be a positive value")
>>> assert(is_int(n) && n>1, "n must be an integer larger than 1")
>>> assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
>>> between -1 and 1")
>>> assert(ir<or, "inside radius (ir/id) must be smaller than
>>> outside radius (or/od)")
>>> assert(all_positive([tooth_angle]) &&
>>> tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
>>> ",360*(n-1)/2/n," for spline with ",n," teeth."))
>>> assert(num_defined([chamfer,rounding]) <=1, "Cannot define
>>> both chamfer and rounding")
>>> assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
>>> chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
>>> assert(is_undef(rounding) || all_nonnegative([rounding]) &&
>>> rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
>>> assert(all_positive([base]), "base must be a positive value") ;
>>> tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
>>> tooth height
>>> cone_height = -tan(cone_angle); // Normalized
>>> height change corresponding to the cone angle
>>> ridge_angle = atan(tooth_height/2 + cone_height);
>>> valley_angle = atan(-tooth_height/2 + cone_height);
>>> angle = 180/n; // Half the angle occupied by each tooth going
>>> around the circle
>>>
>>> factor = crop ? 3 : 1; // Make it oversized when crop is true
>>>
>>> profile = is_undef(rounding) || rounding==0 ?
>>> let(
>>> chamfer=default(chamfer,0),
>>> vchamf = chamfer*(ridge_angle-valley_angle),
>>> pts = [
>>> [-angle*(1-chamfer/2),
>>> valley_angle+vchamf/2],
>>> [-angle*chamfer, ridge_angle-vchamf]
>>> ],
>>> full = deduplicate(concat(pts, reverse(xflip(pts))))
>>> )
>>> back(valley_angle,
>>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
>>> : let(
>>> vround=rounding*(ridge_angle-valley_angle),
>>> profpts = [
>>> [ -angle, valley_angle+vround/2],
>>> [ -angle*(1-rounding/2),
>>> valley_angle+vround/2],
>>> [ -angle*rounding, ridge_angle-vround],
>>> ],
>>> segs = max(16,segs(or*rounding)),
>>> full = concat(profpts, reverse(xflip(profpts))),
>>> skewed = back(valley_angle,
>>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
>>> // Using computed values for the joints
>>> lead to round-off error issues
>>> joints = [(skewed[1]-skewed[0]).x,
>>> (skewed[3]-skewed[2]).x/2,
>>> (skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
>>> roundpts = round_corners(skewed, joint=joints,
>>> closed=false,$fn=segs)
>>> )
>>> roundpts;
>>>
>>> // project spherical coordinate point onto cylinder of radius r
>>> cyl_proj = function (r,theta_phi)
>>> [for(pt=theta_phi)
>>> let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
>>> r * xyz / norm(point2d(xyz))];
>>>
>>> bottom =
>>> min([tan(valley_angle)*ir,tan(valley_angle)*or])-base-cone_height*ir;
>>> safebottom =
>>> min([tan(valley_angle)*ir/factor,tan(valley_angle)*or*factor])-base-(crop?1:0)-cone_height*ir;
>>> ang_ofs = !rot ? -skew*angle
>>> : n%2==0 ? -(angle-skew*angle) - skew*angle
>>> : -angle*(2-skew)-skew*angle;
>>> topinner = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>>> each
>>> zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
>>> topouter = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>>> each
>>> zrot(ang+ang_ofs,cyl_proj(factor*or,profile))]);
>>> botinner = [for(val=topinner) [val.x,val.y,safebottom]];
>>> botouter = [for(val=topouter) [val.x,val.y,safebottom]];
>>> vert = [topouter, topinner, botinner, botouter];
>>>
>>> anchors = [
>>> named_anchor("teeth_bot", [0,0,bottom], DOWN)
>>> ];
>>> attachable(anchor=anchor,spin=spin,orient=orient, r=or,
>>> h=-2*bottom,anchors=anchors){
>>> intersection(){
>>> vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
>>> col_wrap=true, row_wrap=true),convexity=min(10,n));
>>> if (crop)
>>>
>>> zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
>>> }
>>> children();
>>> }
>>> }
>>>
>>>
>>>
>>> On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> I have established that there is an error in the code fragment. The line
>>>>
>>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>>
>>>> Is where the error lies. What should it be? I was assuming that the
>>>> theta for the chamfer “shoulder” point would be proportional to the chamfer
>>>> but it produces a slight error. It is barely noticeable but gets more
>>>> blatant at low tooth counts and high conic.
>>>>
>>>> Anyone see what it should be? I’m guessing there is some trig
>>>> functions involved,but ...
>>>>
>>>> -Bob
>>>>
>>>> On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
>>>> discuss@lists.openscad.org> wrote:
>>>>
>>>> Here is just a code fragment but it gets the point across.
>>>>
>>>> IR = _ir(hs);
>>>> OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
>>>> circumscribing polygon of N
>>>>
>>>> // Ridge Chamfer
>>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>> phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
>>>>
>>>> function profileToooth(r) =
>>>> [spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
>>>> phiCA),
>>>> spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
>>>> spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
>>>> spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
>>>> phiCA)
>>>> ];
>>>>
>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>>

SP
Sanjeev Prabhakar
Thu, Nov 7, 2024 11:24 AM
Thanks David
That book you share is good, but it is taking some time to absorb
On Thu, 7 Nov, 2024, 11:53 am John David, ebo.2112@gmail.com wrote:
very nice! Thank you for sharing ;-)
On Wed, Nov 6, 2024 at 11:59 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
this is the final version (attached is the scad file)
[image: Screenshot 2024-11-07 at 10.26.12 AM.png]
On Thu, 7 Nov 2024 at 09:54, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge
(and slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a
number between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) &&
tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
",360*(n-1)/2/n," for spline with ",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define
both chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value")
;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
tooth height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going
around the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2),
valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts,
reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
col_wrap=true, row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The
line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the
theta for the chamfer “shoulder” point would be proportional to the chamfer
but it produces a slight error. It is barely noticeable but gets more
blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Thanks David
That book you share is good, but it is taking some time to absorb
On Thu, 7 Nov, 2024, 11:53 am John David, <ebo.2112@gmail.com> wrote:
> very nice! Thank you for sharing ;-)
>
> On Wed, Nov 6, 2024 at 11:59 PM Sanjeev Prabhakar via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> this is the final version (attached is the scad file)
>> [image: Screenshot 2024-11-07 at 10.26.12 AM.png]
>>
>> On Thu, 7 Nov 2024 at 09:54, Sanjeev Prabhakar <sprabhakar2006@gmail.com>
>> wrote:
>>
>>> I don't think the straight projection on cylinder will work.
>>> The only way I think this can work is if you project using vectors
>>> considering outer race and inner race, projecting outwards and inwards
>>> respectively on outer and inner cylinder.
>>> picture below can make this clear.
>>> magenta lines are the vectors
>>> [image: Screenshot 2024-11-07 at 9.49.27 AM.png]
>>> [image: Screenshot 2024-11-07 at 9.53.29 AM.png]
>>>
>>> On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> Bob, I did I think exactly the same thing in my code and didn't notice
>>>> anything, but now that you mention it, doing chamfers on an angular basis
>>>> is of course not going to match doing them on a linear basis. So that
>>>> means the geometry changes a bit if you change the chamfer size. This
>>>> isn't necessarily catastrophic, but is a little unexpected, I suppose.
>>>> Generally speaking you can't mate two parts produced with different chamfer
>>>> size anyway, so I'm not sure this is crucial to get right. But in order to
>>>> get it right, I think both thetaCA2 and phiCA are going to need to be
>>>> computed with trig---either that or there's some complicated way of
>>>> computing just one. The question is whether these two parameters can be
>>>> computed independently or are they related in some complicated way.
>>>> Treated as a 2d problem you are trying to get the angle that corresponds to
>>>> a fraction of a chord of the circle, which is a reasonably straight forward
>>>> triangle calculation. I got atan(chamfer*tan(angle)) where angle is
>>>> 180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
>>>> align with the unchamfered. For example:
>>>>
>>>> [image: image.png]
>>>>
>>>> Yellow is unchamfered. Blue has huge chamfer applied only at ridge
>>>> (and slightly larger radius so we can see it clearly). And we see that the
>>>> angle has changed. I actually got less error with the original
>>>> calculation, but that might be because I didn't correct the phi angle only
>>>> the theta angle. (Or maybe I botched the trig.) So I tried computing a
>>>> correction for phi and got ridge_angle-atan(ridge_angle -
>>>> chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
>>>> up correctly. (And the horizontal correction is still worse than not,
>>>> which makes me wonder if the horizontal correction needs to take into
>>>> account the vertical position of the chamfer somehow.) Doing the phi
>>>> correction alone actually is an improvement over no correction.
>>>>
>>>> Here's my current code (without any chamfer corrections). It does
>>>> rounding and skew teeth.
>>>>
>>>> module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
>>>> rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
>>>> {
>>>> ir = get_radius(r=ir,d=id);
>>>> or = get_radius(r=or,d=od);
>>>> dummy = assert(all_positive([ir]), "ir/id must be a positive value")
>>>> assert(all_positive([or]), "or/od must be a positive value")
>>>> assert(is_int(n) && n>1, "n must be an integer larger than 1")
>>>> assert(is_finite(skew) && abs(skew)<=1, "skew must be a
>>>> number between -1 and 1")
>>>> assert(ir<or, "inside radius (ir/id) must be smaller than
>>>> outside radius (or/od)")
>>>> assert(all_positive([tooth_angle]) &&
>>>> tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
>>>> ",360*(n-1)/2/n," for spline with ",n," teeth."))
>>>> assert(num_defined([chamfer,rounding]) <=1, "Cannot define
>>>> both chamfer and rounding")
>>>> assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
>>>> chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
>>>> assert(is_undef(rounding) || all_nonnegative([rounding]) &&
>>>> rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
>>>> assert(all_positive([base]), "base must be a positive value")
>>>> ;
>>>> tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
>>>> tooth height
>>>> cone_height = -tan(cone_angle); // Normalized
>>>> height change corresponding to the cone angle
>>>> ridge_angle = atan(tooth_height/2 + cone_height);
>>>> valley_angle = atan(-tooth_height/2 + cone_height);
>>>> angle = 180/n; // Half the angle occupied by each tooth going
>>>> around the circle
>>>>
>>>> factor = crop ? 3 : 1; // Make it oversized when crop is true
>>>>
>>>> profile = is_undef(rounding) || rounding==0 ?
>>>> let(
>>>> chamfer=default(chamfer,0),
>>>> vchamf = chamfer*(ridge_angle-valley_angle),
>>>> pts = [
>>>> [-angle*(1-chamfer/2),
>>>> valley_angle+vchamf/2],
>>>> [-angle*chamfer, ridge_angle-vchamf]
>>>> ],
>>>> full = deduplicate(concat(pts,
>>>> reverse(xflip(pts))))
>>>> )
>>>> back(valley_angle,
>>>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
>>>> : let(
>>>> vround=rounding*(ridge_angle-valley_angle),
>>>> profpts = [
>>>> [ -angle, valley_angle+vround/2],
>>>> [ -angle*(1-rounding/2),
>>>> valley_angle+vround/2],
>>>> [ -angle*rounding, ridge_angle-vround],
>>>> ],
>>>> segs = max(16,segs(or*rounding)),
>>>> full = concat(profpts, reverse(xflip(profpts))),
>>>> skewed = back(valley_angle,
>>>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
>>>> // Using computed values for the joints
>>>> lead to round-off error issues
>>>> joints = [(skewed[1]-skewed[0]).x,
>>>> (skewed[3]-skewed[2]).x/2,
>>>> (skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
>>>> roundpts = round_corners(skewed, joint=joints,
>>>> closed=false,$fn=segs)
>>>> )
>>>> roundpts;
>>>>
>>>> // project spherical coordinate point onto cylinder of radius r
>>>> cyl_proj = function (r,theta_phi)
>>>> [for(pt=theta_phi)
>>>> let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
>>>> r * xyz / norm(point2d(xyz))];
>>>>
>>>> bottom =
>>>> min([tan(valley_angle)*ir,tan(valley_angle)*or])-base-cone_height*ir;
>>>> safebottom =
>>>> min([tan(valley_angle)*ir/factor,tan(valley_angle)*or*factor])-base-(crop?1:0)-cone_height*ir;
>>>> ang_ofs = !rot ? -skew*angle
>>>> : n%2==0 ? -(angle-skew*angle) - skew*angle
>>>> : -angle*(2-skew)-skew*angle;
>>>> topinner = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>>>> each
>>>> zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
>>>> topouter = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>>>> each
>>>> zrot(ang+ang_ofs,cyl_proj(factor*or,profile))]);
>>>> botinner = [for(val=topinner) [val.x,val.y,safebottom]];
>>>> botouter = [for(val=topouter) [val.x,val.y,safebottom]];
>>>> vert = [topouter, topinner, botinner, botouter];
>>>>
>>>> anchors = [
>>>> named_anchor("teeth_bot", [0,0,bottom], DOWN)
>>>> ];
>>>> attachable(anchor=anchor,spin=spin,orient=orient, r=or,
>>>> h=-2*bottom,anchors=anchors){
>>>> intersection(){
>>>> vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
>>>> col_wrap=true, row_wrap=true),convexity=min(10,n));
>>>> if (crop)
>>>>
>>>> zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
>>>> }
>>>> children();
>>>> }
>>>> }
>>>>
>>>>
>>>>
>>>> On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
>>>> discuss@lists.openscad.org> wrote:
>>>>
>>>>> I have established that there is an error in the code fragment. The
>>>>> line
>>>>>
>>>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>>>
>>>>> Is where the error lies. What should it be? I was assuming that the
>>>>> theta for the chamfer “shoulder” point would be proportional to the chamfer
>>>>> but it produces a slight error. It is barely noticeable but gets more
>>>>> blatant at low tooth counts and high conic.
>>>>>
>>>>> Anyone see what it should be? I’m guessing there is some trig
>>>>> functions involved,but ...
>>>>>
>>>>> -Bob
>>>>>
>>>>> On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
>>>>> discuss@lists.openscad.org> wrote:
>>>>>
>>>>> Here is just a code fragment but it gets the point across.
>>>>>
>>>>> IR = _ir(hs);
>>>>> OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
>>>>> circumscribing polygon of N
>>>>>
>>>>> // Ridge Chamfer
>>>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>>> phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
>>>>>
>>>>> function profileToooth(r) =
>>>>> [spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
>>>>> phiCA),
>>>>> spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
>>>>> spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
>>>>> spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
>>>>> phiCA)
>>>>> ];
>>>>>
>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
>

AM
Adrian Mariano
Thu, Nov 7, 2024 11:29 AM
In the to picture, there is no cylinder pictured, but some complicated
shape with multiple curves, some of which are not even circular arcs. So I
don't understand that picture. You can try the code I posted earlier,
which uses the cylinder projection approach.
On Thu, Nov 7, 2024 at 6:23 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
All the magenta lines are vectors, you can think of them originating from
any side of the line.
Each line intersects a circumscribing cylinder outer or inner and that
forms the circular hirth coupling.
On Thu, 7 Nov, 2024, 4:40 pm Adrian Mariano, avm4@cornell.edu wrote:
I do not understand the pictures. Or at least the top one is
mystifying. The bottom one looks like it could describe the process: the
projection is along vectors that originate at the origin and yes, you have
a separate projection onto the inner and outer cylinder.
On Wed, Nov 6, 2024 at 11:24 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge
(and slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a
number between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) &&
tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
",360*(n-1)/2/n," for spline with ",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define
both chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value")
;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
tooth height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going
around the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2),
valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts,
reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
col_wrap=true, row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The
line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the
theta for the chamfer “shoulder” point would be proportional to the chamfer
but it produces a slight error. It is barely noticeable but gets more
blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
In the to picture, there is no cylinder pictured, but some complicated
shape with multiple curves, some of which are not even circular arcs. So I
don't understand that picture. You can try the code I posted earlier,
which uses the cylinder projection approach.
On Thu, Nov 7, 2024 at 6:23 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> All the magenta lines are vectors, you can think of them originating from
> any side of the line.
>
> Each line intersects a circumscribing cylinder outer or inner and that
> forms the circular hirth coupling.
>
>
>
> On Thu, 7 Nov, 2024, 4:40 pm Adrian Mariano, <avm4@cornell.edu> wrote:
>
>> I do not understand the pictures. Or at least the top one is
>> mystifying. The bottom one looks like it could describe the process: the
>> projection is along vectors that originate at the origin and yes, you have
>> a separate projection onto the inner and outer cylinder.
>>
>> On Wed, Nov 6, 2024 at 11:24 PM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> I don't think the straight projection on cylinder will work.
>>> The only way I think this can work is if you project using vectors
>>> considering outer race and inner race, projecting outwards and inwards
>>> respectively on outer and inner cylinder.
>>> picture below can make this clear.
>>> magenta lines are the vectors
>>> [image: Screenshot 2024-11-07 at 9.49.27 AM.png]
>>> [image: Screenshot 2024-11-07 at 9.53.29 AM.png]
>>>
>>> On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> Bob, I did I think exactly the same thing in my code and didn't notice
>>>> anything, but now that you mention it, doing chamfers on an angular basis
>>>> is of course not going to match doing them on a linear basis. So that
>>>> means the geometry changes a bit if you change the chamfer size. This
>>>> isn't necessarily catastrophic, but is a little unexpected, I suppose.
>>>> Generally speaking you can't mate two parts produced with different chamfer
>>>> size anyway, so I'm not sure this is crucial to get right. But in order to
>>>> get it right, I think both thetaCA2 and phiCA are going to need to be
>>>> computed with trig---either that or there's some complicated way of
>>>> computing just one. The question is whether these two parameters can be
>>>> computed independently or are they related in some complicated way.
>>>> Treated as a 2d problem you are trying to get the angle that corresponds to
>>>> a fraction of a chord of the circle, which is a reasonably straight forward
>>>> triangle calculation. I got atan(chamfer*tan(angle)) where angle is
>>>> 180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
>>>> align with the unchamfered. For example:
>>>>
>>>> [image: image.png]
>>>>
>>>> Yellow is unchamfered. Blue has huge chamfer applied only at ridge
>>>> (and slightly larger radius so we can see it clearly). And we see that the
>>>> angle has changed. I actually got less error with the original
>>>> calculation, but that might be because I didn't correct the phi angle only
>>>> the theta angle. (Or maybe I botched the trig.) So I tried computing a
>>>> correction for phi and got ridge_angle-atan(ridge_angle -
>>>> chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
>>>> up correctly. (And the horizontal correction is still worse than not,
>>>> which makes me wonder if the horizontal correction needs to take into
>>>> account the vertical position of the chamfer somehow.) Doing the phi
>>>> correction alone actually is an improvement over no correction.
>>>>
>>>> Here's my current code (without any chamfer corrections). It does
>>>> rounding and skew teeth.
>>>>
>>>> module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
>>>> rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
>>>> {
>>>> ir = get_radius(r=ir,d=id);
>>>> or = get_radius(r=or,d=od);
>>>> dummy = assert(all_positive([ir]), "ir/id must be a positive value")
>>>> assert(all_positive([or]), "or/od must be a positive value")
>>>> assert(is_int(n) && n>1, "n must be an integer larger than 1")
>>>> assert(is_finite(skew) && abs(skew)<=1, "skew must be a
>>>> number between -1 and 1")
>>>> assert(ir<or, "inside radius (ir/id) must be smaller than
>>>> outside radius (or/od)")
>>>> assert(all_positive([tooth_angle]) &&
>>>> tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
>>>> ",360*(n-1)/2/n," for spline with ",n," teeth."))
>>>> assert(num_defined([chamfer,rounding]) <=1, "Cannot define
>>>> both chamfer and rounding")
>>>> assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
>>>> chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
>>>> assert(is_undef(rounding) || all_nonnegative([rounding]) &&
>>>> rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
>>>> assert(all_positive([base]), "base must be a positive value")
>>>> ;
>>>> tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
>>>> tooth height
>>>> cone_height = -tan(cone_angle); // Normalized
>>>> height change corresponding to the cone angle
>>>> ridge_angle = atan(tooth_height/2 + cone_height);
>>>> valley_angle = atan(-tooth_height/2 + cone_height);
>>>> angle = 180/n; // Half the angle occupied by each tooth going
>>>> around the circle
>>>>
>>>> factor = crop ? 3 : 1; // Make it oversized when crop is true
>>>>
>>>> profile = is_undef(rounding) || rounding==0 ?
>>>> let(
>>>> chamfer=default(chamfer,0),
>>>> vchamf = chamfer*(ridge_angle-valley_angle),
>>>> pts = [
>>>> [-angle*(1-chamfer/2),
>>>> valley_angle+vchamf/2],
>>>> [-angle*chamfer, ridge_angle-vchamf]
>>>> ],
>>>> full = deduplicate(concat(pts,
>>>> reverse(xflip(pts))))
>>>> )
>>>> back(valley_angle,
>>>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
>>>> : let(
>>>> vround=rounding*(ridge_angle-valley_angle),
>>>> profpts = [
>>>> [ -angle, valley_angle+vround/2],
>>>> [ -angle*(1-rounding/2),
>>>> valley_angle+vround/2],
>>>> [ -angle*rounding, ridge_angle-vround],
>>>> ],
>>>> segs = max(16,segs(or*rounding)),
>>>> full = concat(profpts, reverse(xflip(profpts))),
>>>> skewed = back(valley_angle,
>>>> skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
>>>> // Using computed values for the joints
>>>> lead to round-off error issues
>>>> joints = [(skewed[1]-skewed[0]).x,
>>>> (skewed[3]-skewed[2]).x/2,
>>>> (skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
>>>> roundpts = round_corners(skewed, joint=joints,
>>>> closed=false,$fn=segs)
>>>> )
>>>> roundpts;
>>>>
>>>> // project spherical coordinate point onto cylinder of radius r
>>>> cyl_proj = function (r,theta_phi)
>>>> [for(pt=theta_phi)
>>>> let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
>>>> r * xyz / norm(point2d(xyz))];
>>>>
>>>> bottom =
>>>> min([tan(valley_angle)*ir,tan(valley_angle)*or])-base-cone_height*ir;
>>>> safebottom =
>>>> min([tan(valley_angle)*ir/factor,tan(valley_angle)*or*factor])-base-(crop?1:0)-cone_height*ir;
>>>> ang_ofs = !rot ? -skew*angle
>>>> : n%2==0 ? -(angle-skew*angle) - skew*angle
>>>> : -angle*(2-skew)-skew*angle;
>>>> topinner = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>>>> each
>>>> zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
>>>> topouter = down(cone_height*ir,[for(ang=lerpn(0,360,n,endpoint=false))
>>>> each
>>>> zrot(ang+ang_ofs,cyl_proj(factor*or,profile))]);
>>>> botinner = [for(val=topinner) [val.x,val.y,safebottom]];
>>>> botouter = [for(val=topouter) [val.x,val.y,safebottom]];
>>>> vert = [topouter, topinner, botinner, botouter];
>>>>
>>>> anchors = [
>>>> named_anchor("teeth_bot", [0,0,bottom], DOWN)
>>>> ];
>>>> attachable(anchor=anchor,spin=spin,orient=orient, r=or,
>>>> h=-2*bottom,anchors=anchors){
>>>> intersection(){
>>>> vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
>>>> col_wrap=true, row_wrap=true),convexity=min(10,n));
>>>> if (crop)
>>>>
>>>> zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
>>>> }
>>>> children();
>>>> }
>>>> }
>>>>
>>>>
>>>>
>>>> On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
>>>> discuss@lists.openscad.org> wrote:
>>>>
>>>>> I have established that there is an error in the code fragment. The
>>>>> line
>>>>>
>>>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>>>
>>>>> Is where the error lies. What should it be? I was assuming that the
>>>>> theta for the chamfer “shoulder” point would be proportional to the chamfer
>>>>> but it produces a slight error. It is barely noticeable but gets more
>>>>> blatant at low tooth counts and high conic.
>>>>>
>>>>> Anyone see what it should be? I’m guessing there is some trig
>>>>> functions involved,but ...
>>>>>
>>>>> -Bob
>>>>>
>>>>> On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
>>>>> discuss@lists.openscad.org> wrote:
>>>>>
>>>>> Here is just a code fragment but it gets the point across.
>>>>>
>>>>> IR = _ir(hs);
>>>>> OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
>>>>> circumscribing polygon of N
>>>>>
>>>>> // Ridge Chamfer
>>>>> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>>>>> phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
>>>>>
>>>>> function profileToooth(r) =
>>>>> [spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
>>>>> phiCA),
>>>>> spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
>>>>> spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
>>>>> spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
>>>>> phiCA)
>>>>> ];
>>>>>
>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>>

RW
Raymond West
Thu, Nov 7, 2024 12:33 PM
Hi Sanjeev,
Thanks for testing it, I get no warnings or errors, unless i use less
than three ridges, or other inappropriate values. I'm guessing it's an
openscad version difference. I think my geometry is good enough for me,
but probably not bullet proof.
On 06/11/2024 02:21, Sanjeev Prabhakar via Discuss wrote:
Hi Ray
I tried your code and it is almost instant render and there are no
issues in the manifold which I use during f6 render. There are some
warnings but that's fine
On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss
discuss@lists.openscad.org wrote:
Hi Sanjeev,
Thanks for testing it, I get no warnings or errors, unless i use less
than three ridges, or other inappropriate values. I'm guessing it's an
openscad version difference. I think my geometry is good enough for me,
but probably not bullet proof.
On 06/11/2024 02:21, Sanjeev Prabhakar via Discuss wrote:
> Hi Ray
> I tried your code and it is almost instant render and there are no
> issues in the manifold which I use during f6 render. There are some
> warnings but that's fine
>
> On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss
> <discuss@lists.openscad.org> wrote:
>

RW
Raymond West
Thu, Nov 7, 2024 12:49 PM
Hi Ken,
Thanks for testing, I get no errors with OpenSCAD version 2024.02.19
(git 5cfd4dbe0), but it may be other reasons. I think my geometry is
good enough with reasonable parameters. However, I expect there is the
usual z fighting taking place, since the various parts probably do not
overlap sufficiently in some cases. I expect, using cadquery (which uses
a different rendering engine) the geometry may work with different errors.
On 05/11/2024 23:32, Ken via Discuss wrote:
I tried it on mine- I'm using version 2024.10.2 git e972ed84e.
F5 takes 0.059 seconds, f6 0.096 seconds.
I get-
"WARNING: PolySet -> Manifold conversion failed: NotManifold
Trying to repair and reconstruct mesh.."
four times, then it continues to render with no further errors. I have
just finished printing two of them so I can have a play.
On 2024-11-06 09:27, Adrian Mariano via Discuss wrote:
Ray, I tried your code and (1) preview is very very slow on my
machine and (2) render gives
Rendering Polygon Mesh using CGAL...
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
Geometries in cache: 9903
I'm now convinced that Bob has the right basic approach. The key
thing is the idea of projecting onto a cylinder. Working in spherical
coordinates never made sense to me, but for some reason the idea of
just projecting points onto a cylinder didn't occur to me. (At one
point I thought about doing it, but with equations, not with code,
which was a bad idea.) With this insight I can now make roundings
while creating the object as a single polyhedron:
image.png
On Tue, Nov 5, 2024 at 12:54 PM Raymond West via Discuss
discuss@lists.openscad.org wrote:
I've modified it slightly, to allow the tooth angle to be set -
In manufacturing, most likely a 60 or 90 degree angle. I've also
included the angle to set the rotary table, and added a method of
flattening the tips. I think this could 3d printed OK, I've yet
to test. The stl would not be used in any other manufacturing
process, afaik. For machining, It could be set up directly from
the parameters. I've attached the code below. The flattening of
the peaks give a slight taper. Adding an extra triangle to the
polyhedron, could generate a more tapered width to the flat top,
but for whatever use I may put this too, if any, it is unlikely
to make much difference.
The code will produce a viable stl, for any number of teeth,
including three and upwards, and it f6 renders fast enough.
Here is a link to some curvic coupling design, which is a bit
more involved to generate -
https://www.geartechnology.com/articles/20867-curvic-coupling-design.
On 04/11/2024 17:05, Raymond West via Discuss wrote:
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
A baby can be defined as an ego with a noise at one end and a smell at the other.
Your job as parents is to teach them to control all three.
My job as a grandad is to tell you how you are doing it all wrong!
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
Hi Ken,
Thanks for testing, I get no errors with OpenSCAD version 2024.02.19
(git 5cfd4dbe0), but it may be other reasons. I think my geometry is
good enough with reasonable parameters. However, I expect there is the
usual z fighting taking place, since the various parts probably do not
overlap sufficiently in some cases. I expect, using cadquery (which uses
a different rendering engine) the geometry may work with different errors.
On 05/11/2024 23:32, Ken via Discuss wrote:
> I tried it on mine- I'm using version 2024.10.2 git e972ed84e.
> F5 takes 0.059 seconds, f6 0.096 seconds.
> I get-
>
> "WARNING: PolySet -> Manifold conversion failed: NotManifold
> Trying to repair and reconstruct mesh.."
>
> four times, then it continues to render with no further errors. I have
> just finished printing two of them so I can have a play.
>
>
> On 2024-11-06 09:27, Adrian Mariano via Discuss wrote:
>> Ray, I tried your code and (1) preview is very very slow on my
>> machine and (2) render gives
>>
>> Rendering Polygon Mesh using CGAL...
>>
>> ERROR: The given mesh is not closed! Unable to convert to
>> CGAL_Nef_Polyhedron.
>>
>> ERROR: The given mesh is not closed! Unable to convert to
>> CGAL_Nef_Polyhedron.
>>
>> ERROR: The given mesh is not closed! Unable to convert to
>> CGAL_Nef_Polyhedron.
>>
>> ERROR: The given mesh is not closed! Unable to convert to
>> CGAL_Nef_Polyhedron.
>>
>> ERROR: The given mesh is not closed! Unable to convert to
>> CGAL_Nef_Polyhedron.
>>
>> Geometries in cache: 9903
>>
>>
>> I'm now convinced that Bob has the right basic approach. The key
>> thing is the idea of projecting onto a cylinder. Working in spherical
>> coordinates never made sense to me, but for some reason the idea of
>> just projecting points onto a cylinder didn't occur to me. (At one
>> point I thought about doing it, but with equations, not with code,
>> which was a bad idea.) With this insight I can now make roundings
>> while creating the object as a single polyhedron:
>>
>>
>> image.png
>>
>>
>>
>>
>> On Tue, Nov 5, 2024 at 12:54 PM Raymond West via Discuss
>> <discuss@lists.openscad.org> wrote:
>>
>> I've modified it slightly, to allow the tooth angle to be set -
>> In manufacturing, most likely a 60 or 90 degree angle. I've also
>> included the angle to set the rotary table, and added a method of
>> flattening the tips. I think this could 3d printed OK, I've yet
>> to test. The stl would not be used in any other manufacturing
>> process, afaik. For machining, It could be set up directly from
>> the parameters. I've attached the code below. The flattening of
>> the peaks give a slight taper. Adding an extra triangle to the
>> polyhedron, could generate a more tapered width to the flat top,
>> but for whatever use I may put this too, if any, it is unlikely
>> to make much difference.
>>
>> The code will produce a viable stl, for any number of teeth,
>> including three and upwards, and it f6 renders fast enough.
>>
>> Here is a link to some curvic coupling design, which is a bit
>> more involved to generate -
>> https://www.geartechnology.com/articles/20867-curvic-coupling-design.
>>
>>
>> On 04/11/2024 17:05, Raymond West via Discuss wrote:
>>>
>>> found it- etc.
>>>
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email todiscuss-leave@lists.openscad.org
>
> --
> Cheers, Ken
> bats059@gmail.com
> https://vk7krj.com
> https://vk7krj.com/running.html
> ----------------------------------------
> A baby can be defined as an ego with a noise at one end and a smell at the other.
> Your job as parents is to teach them to control all three.
> My job as a grandad is to tell you how you are doing it all wrong!
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email todiscuss-leave@lists.openscad.org
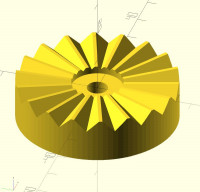


SP
Sanjeev Prabhakar
Thu, Nov 7, 2024 2:18 PM
I think my geometry is good enough for me
Yes sure It works and that's what matters. anyways it's not a fatal error
On Thu, 7 Nov 2024 at 18:03, Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
Hi Sanjeev,
Thanks for testing it, I get no warnings or errors, unless i use less than
three ridges, or other inappropriate values. I'm guessing it's an openscad
version difference. I think my geometry is good enough for me, but probably
not bullet proof.
On 06/11/2024 02:21, Sanjeev Prabhakar via Discuss wrote:
Hi Ray
I tried your code and it is almost instant render and there are no issues
in the manifold which I use during f6 render. There are some warnings but
that's fine
On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
> I think my geometry is good enough for me
Yes sure It works and that's what matters. anyways it's not a fatal error
On Thu, 7 Nov 2024 at 18:03, Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
> Hi Sanjeev,
>
> Thanks for testing it, I get no warnings or errors, unless i use less than
> three ridges, or other inappropriate values. I'm guessing it's an openscad
> version difference. I think my geometry is good enough for me, but probably
> not bullet proof.
> On 06/11/2024 02:21, Sanjeev Prabhakar via Discuss wrote:
>
> Hi Ray
> I tried your code and it is almost instant render and there are no issues
> in the manifold which I use during f6 render. There are some warnings but
> that's fine
>
> On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss <
> discuss@lists.openscad.org> wrote:
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Thu, Nov 7, 2024 8:15 PM
All errors are fatal when you run with the stop on first warning feature,
which is generally necessary to avoid overwhelming useless cascading error
messages.
Under the stable openscad that I used the model fails to render using the
code exactly as posted. This is because it contains some reversed faces
that can be seen with thrown together. I didn’t know that manifold would
fix those with a warning. I generally prefer to use polyhedron creation
tools to make fully valid face sets.
Even after fixing that problem something else is wrong because I get the
message that the object may not be a valid 2-manifold. I don’t know what
the other problem is. Maybe it’s because wedges touch at their edges?
The problem of sluggish preview also remains.
On Thu, Nov 7, 2024 at 09:19 Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I think my geometry is good enough for me
Yes sure It works and that's what matters. anyways it's not a fatal error
On Thu, 7 Nov 2024 at 18:03, Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
Hi Sanjeev,
Thanks for testing it, I get no warnings or errors, unless i use less
than three ridges, or other inappropriate values. I'm guessing it's an
openscad version difference. I think my geometry is good enough for me, but
probably not bullet proof.
On 06/11/2024 02:21, Sanjeev Prabhakar via Discuss wrote:
Hi Ray
I tried your code and it is almost instant render and there are no issues
in the manifold which I use during f6 render. There are some warnings but
that's fine
On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
All errors are fatal when you run with the stop on first warning feature,
which is generally necessary to avoid overwhelming useless cascading error
messages.
Under the stable openscad that I used the model fails to render using the
code exactly as posted. This is because it contains some reversed faces
that can be seen with thrown together. I didn’t know that manifold would
fix those with a warning. I generally prefer to use polyhedron creation
tools to make fully valid face sets.
Even after fixing that problem something else is wrong because I get the
message that the object may not be a valid 2-manifold. I don’t know what
the other problem is. Maybe it’s because wedges touch at their edges?
The problem of sluggish preview also remains.
On Thu, Nov 7, 2024 at 09:19 Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
> > I think my geometry is good enough for me
>
> Yes sure It works and that's what matters. anyways it's not a fatal error
>
> On Thu, 7 Nov 2024 at 18:03, Raymond West via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> Hi Sanjeev,
>>
>> Thanks for testing it, I get no warnings or errors, unless i use less
>> than three ridges, or other inappropriate values. I'm guessing it's an
>> openscad version difference. I think my geometry is good enough for me, but
>> probably not bullet proof.
>> On 06/11/2024 02:21, Sanjeev Prabhakar via Discuss wrote:
>>
>> Hi Ray
>> I tried your code and it is almost instant render and there are no issues
>> in the manifold which I use during f6 render. There are some warnings but
>> that's fine
>>
>> On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Thu, Nov 7, 2024 10:13 PM
I think that to get this right you basically need to take the top point of
the triangle and one of the bottom points of the triangle in their position
projected onto the cylinder, represent in cartesian coordinates, then
interpolate appropriately between them by the chamfer fraction, then
convert back to spherical coordinates to extract the angles. You can work
through those steps to get some complicated formula, but it looked messy.
I couldn't think of any simpler approach.
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the theta
for the chamfer “shoulder” point would be proportional to the chamfer but
it produces a slight error. It is barely noticeable but gets more blatant
at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) + phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I think that to get this right you basically need to take the top point of
the triangle and one of the bottom points of the triangle in their position
projected onto the cylinder, represent in cartesian coordinates, then
interpolate appropriately between them by the chamfer fraction, then
convert back to spherical coordinates to extract the angles. You can work
through those steps to get some complicated formula, but it looked messy.
I couldn't think of any simpler approach.
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
> I have established that there is an error in the code fragment. The line
>
> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
>
> Is where the error lies. What should it be? I was assuming that the theta
> for the chamfer “shoulder” point would be proportional to the chamfer but
> it produces a slight error. It is barely noticeable but gets more blatant
> at low tooth counts and high conic.
>
> Anyone see what it should be? I’m guessing there is some trig
> functions involved,but ...
>
> -Bob
>
> On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
> discuss@lists.openscad.org> wrote:
>
> Here is just a code fragment but it gets the point across.
>
> IR = _ir(hs);
> OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
> circumscribing polygon of N
>
> // Ridge Chamfer
> thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
> phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
>
> function profileToooth(r) =
> [spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
> phiCA),
> spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
> spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
> spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) + phiCA)
> ];
>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

BC
Bob Carlson
Fri, Nov 8, 2024 4:39 PM
That sounds promising. I tried a lot of stuff but not that and nothing worked quite right. I’ve tweaked my code now to make the chamfer by subtracting later. It’s quite easy. The other thing I did is make 2 half tooth profiles instead of one whole. Now N = 2 works. I also found that skin() did not work at low tooth counts and had to use a combination of skin and hull. If two profiles are very different sizes and far apart, that seemed to be the problem area. I use skin to make thin wafers then hull the wafers together. I suppose some schemes where I generate many profiles close together would work too.
Maybe after I finish this version I’m make one more trial of your idea.
-Bob
On Nov 7, 2024, at 15:13, Adrian Mariano avm4@cornell.edu wrote:
I think that to get this right you basically need to take the top point of the triangle and one of the bottom points of the triangle in their position projected onto the cylinder, represent in cartesian coordinates, then interpolate appropriately between them by the chamfer fraction, then convert back to spherical coordinates to extract the angles. You can work through those steps to get some complicated formula, but it looked messy. I couldn't think of any simpler approach.
That sounds promising. I tried a lot of stuff but not that and nothing worked quite right. I’ve tweaked my code now to make the chamfer by subtracting later. It’s quite easy. The other thing I did is make 2 half tooth profiles instead of one whole. Now N = 2 works. I also found that skin() did not work at low tooth counts and had to use a combination of skin and hull. If two profiles are very different sizes and far apart, that seemed to be the problem area. I use skin to make thin wafers then hull the wafers together. I suppose some schemes where I generate many profiles close together would work too.
Maybe after I finish this version I’m make one more trial of your idea.
-Bob
> On Nov 7, 2024, at 15:13, Adrian Mariano <avm4@cornell.edu> wrote:
>
> I think that to get this right you basically need to take the top point of the triangle and one of the bottom points of the triangle in their position projected onto the cylinder, represent in cartesian coordinates, then interpolate appropriately between them by the chamfer fraction, then convert back to spherical coordinates to extract the angles. You can work through those steps to get some complicated formula, but it looked messy. I couldn't think of any simpler approach.
>