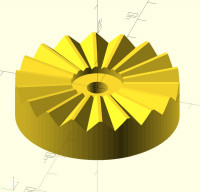
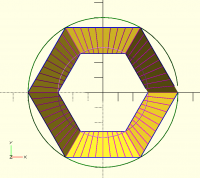
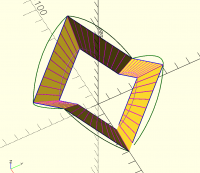
hirth joint
I had been using spherical coordinates and that made it very easy to construct the part using only the 3 angles, groove angle, ridge angle and tooth angle (radial between teeth). Since I have been specifying the chamfer as a percentage of the tooth height, I realized that finding the angles for the chamfers was easy too since everything is proportional including the angles.
The final realization I had though is that normal spherical coordinates did not produce quite the right result as the radii I know are the inner and outer ones. These lie on a cylinder not a sphere. I looked into cylinder_to_xyz in BOSL2 and found that it uses (r, theta, z), spherical uses (r, theta, phi). I needed something else. I created sperical2_to_xyz(r, theta, phi). This is the same as spherical but r is the radius in the XY plane, not in XYZ. It was quite easy to alter the spherical_to_xyz code to get what I wanted.
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) + phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) + phiCA)
];
It works down to N = 3 and could work for N = 2 if the profile were changed to a half tooth. I used skin at first but that breaks down at low tooth counts. I also found that using the tooth profile to produce the groove chamfer didn’t work very well with skin or hull, so I now do that as part of adding the base. I’ll post more complete code soon as I can.
-Bob

On Nov 4, 2024, at 10:33, Raymond West via Discuss discuss@lists.openscad.org wrote:
You have a steeper angle, and higher tension on the centre fixing to improve grip, I guess. The idea of the tapered sides is for ease of manufacturing. To get vertical sides, then it would involve more passes of the grinding wheel/mill. With a 'V' shape, you get more strength at the root, compared to square, (acme thread is stronger than square, plus can use a split nut - not relevant in this case).
On 04/11/2024 09:48, nop head via Discuss wrote:
A lot of discussion but it doesn't look like a useful coupling to me as it will always try to force itself apart. Wouldn't straight sided teeth with a chamfer to aid initial engagement be better.
On Mon, 4 Nov 2024 at 02:47, Sanjeev Prabhakar via Discuss <discuss@lists.openscad.org mailto:discuss@lists.openscad.org> wrote:
And the YouTube video is here in case anyone is interested :
https://youtu.be/Wp8q71eMqrE?si=fY1AxbXp8itbZRm7
On Mon, 4 Nov 2024, 08:10 Sanjeev Prabhakar, <sprabhakar2006@gmail.com mailto:sprabhakar2006@gmail.com> wrote:
I have posted my explanation here:
https://github.com/sprabhakar2006/openSCAD/blob/main/explanation%20of%20approaches/explanation%20hirth%20coupling.pdf
because the file size became 1.5 mb
On Mon, 4 Nov 2024 at 07:38, Adrian Mariano via Discuss <discuss@lists.openscad.org mailto:discuss@lists.openscad.org> wrote:
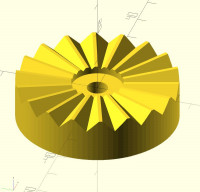
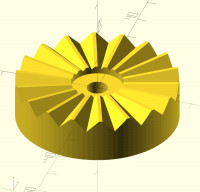
Since a new thread was requested, I'm starting a new thread. I completed an implementation based on the principles I previously described of tilting the triangle. One thing that I didn't make clear is that even though the errors are small at high tooth counts, those errors can make the polyhedron invalid. Part of the intention of my approach was to construct the hirth joint as a single polyhedron. If you're willing to accept that a 30 tooth joint is a 60 sided polyhedron then you don't need the extra complications of intersecting with a tube.
I thought it would be a simple matter to round the valleys, but I was wrong. I can round the tooth tips, but not the valleys because the tilt of the triangle causes a rounding profile to stick out and create a funny ridge along the valley. Perhaps the approach can be adapted to use projection instead of tilt?
Here's a 16 tooth example:
<image.png>
Here's 8 teeth:
<image.png>
Code is attached. A significant amount of complication arose from calculating the location of the bottoms of the valleys in the case where you crop the part with a cylinder. Code attached.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org mailto:discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org mailto:discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org mailto:discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I've modified it slightly, to allow the tooth angle to be set - In
manufacturing, most likely a 60 or 90 degree angle. I've also included
the angle to set the rotary table, and added a method of flattening the
tips. I think this could 3d printed OK, I've yet to test. The stl would
not be used in any other manufacturing process, afaik. For machining, It
could be set up directly from the parameters. I've attached the code
below. The flattening of the peaks give a slight taper. Adding an extra
triangle to the polyhedron, could generate a more tapered width to the
flat top, but for whatever use I may put this too, if any, it is
unlikely to make much difference.
The code will produce a viable stl, for any number of teeth, including
three and upwards, and it f6 renders fast enough.
Here is a link to some curvic coupling design, which is a bit more
involved to generate -
https://www.geartechnology.com/articles/20867-curvic-coupling-design.
On 04/11/2024 17:05, Raymond West via Discuss wrote:
found it- etc.
Ray, I tried your code and (1) preview is very very slow on my machine and
(2) render gives
Rendering Polygon Mesh using CGAL...
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
Geometries in cache: 9903
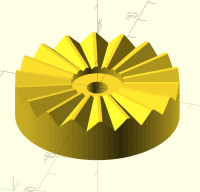
I'm now convinced that Bob has the right basic approach. The key thing is
the idea of projecting onto a cylinder. Working in spherical coordinates
never made sense to me, but for some reason the idea of just projecting
points onto a cylinder didn't occur to me. (At one point I thought about
doing it, but with equations, not with code, which was a bad idea.) With
this insight I can now make roundings while creating the object as a single
polyhedron:
[image: image.png]
On Tue, Nov 5, 2024 at 12:54 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
I've modified it slightly, to allow the tooth angle to be set - In
manufacturing, most likely a 60 or 90 degree angle. I've also included the
angle to set the rotary table, and added a method of flattening the tips. I
think this could 3d printed OK, I've yet to test. The stl would not be used
in any other manufacturing process, afaik. For machining, It could be set
up directly from the parameters. I've attached the code below. The
flattening of the peaks give a slight taper. Adding an extra triangle to
the polyhedron, could generate a more tapered width to the flat top, but
for whatever use I may put this too, if any, it is unlikely to make much
difference.
The code will produce a viable stl, for any number of teeth, including
three and upwards, and it f6 renders fast enough.
Here is a link to some curvic coupling design, which is a bit more
involved to generate -
https://www.geartechnology.com/articles/20867-curvic-coupling-design.
On 04/11/2024 17:05, Raymond West via Discuss wrote:
found it- etc.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I tried it on mine- I'm using version 2024.10.2 git e972ed84e.
F5 takes 0.059 seconds, f6 0.096 seconds.
I get-
"WARNING: PolySet -> Manifold conversion failed: NotManifold
Trying to repair and reconstruct mesh.."
four times, then it continues to render with no further errors. I have just finished printing two of them so I can have a play.
On 2024-11-06 09:27, Adrian Mariano via Discuss wrote:
Ray, I tried your code and (1) preview is very very slow on my machine and (2) render gives
Rendering Polygon Mesh using CGAL...
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
Geometries in cache: 9903
I'm now convinced that Bob has the right basic approach. The key thing is the idea of projecting onto a cylinder. Working in spherical coordinates never made sense to me, but for some reason the idea of just projecting points onto a cylinder didn't occur to me. (At one point I thought about doing it, but with equations, not with code, which was a bad idea.) With this insight I can now make roundings while creating the object as a single polyhedron:
image.png
On Tue, Nov 5, 2024 at 12:54 PM Raymond West via Discuss discuss@lists.openscad.org wrote:
I've modified it slightly, to allow the tooth angle to be set - In manufacturing, most likely a 60 or 90 degree angle. I've also included the angle to set the rotary table, and added a method of flattening the tips. I think this could 3d printed OK, I've yet to test. The stl would not be used in any other manufacturing process, afaik. For machining, It could be set up directly from the parameters. I've attached the code below. The flattening of the peaks give a slight taper. Adding an extra triangle to the polyhedron, could generate a more tapered width to the flat top, but for whatever use I may put this too, if any, it is unlikely to make much difference.
The code will produce a viable stl, for any number of teeth, including three and upwards, and it f6 renders fast enough.
Here is a link to some curvic coupling design, which is a bit more involved to generate - https://www.geartechnology.com/articles/20867-curvic-coupling-design.
On 04/11/2024 17:05, Raymond West via Discuss wrote:
found it- etc.
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
--
Cheers, Ken
bats059@gmail.com
https://vk7krj.com
https://vk7krj.com/running.html
A baby can be defined as an ego with a noise at one end and a smell at the other.
Your job as parents is to teach them to control all three.
My job as a grandad is to tell you how you are doing it all wrong!
Hi Ray
I tried your code and it is almost instant render and there are no issues
in the manifold which I use during f6 render. There are some warnings but
that's fine
On Tue, 5 Nov 2024 at 23:24, Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
I've modified it slightly, to allow the tooth angle to be set - In
manufacturing, most likely a 60 or 90 degree angle. I've also included the
angle to set the rotary table, and added a method of flattening the tips. I
think this could 3d printed OK, I've yet to test. The stl would not be used
in any other manufacturing process, afaik. For machining, It could be set
up directly from the parameters. I've attached the code below. The
flattening of the peaks give a slight taper. Adding an extra triangle to
the polyhedron, could generate a more tapered width to the flat top, but
for whatever use I may put this too, if any, it is unlikely to make much
difference.
The code will produce a viable stl, for any number of teeth, including
three and upwards, and it f6 renders fast enough.
Here is a link to some curvic coupling design, which is a bit more
involved to generate -
https://www.geartechnology.com/articles/20867-curvic-coupling-design.
On 04/11/2024 17:05, Raymond West via Discuss wrote:
found it- etc.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the theta for the chamfer “shoulder” point would be proportional to the chamfer but it produces a slight error. It is barely noticeable but gets more blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss discuss@lists.openscad.org wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) + phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) + phiCA)
];
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
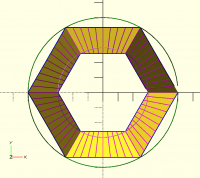
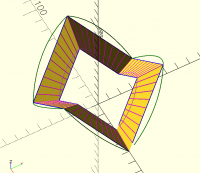
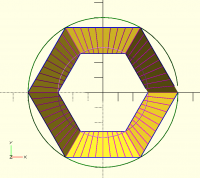
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
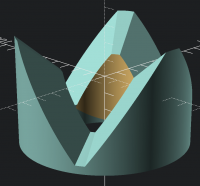
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does rounding
and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than outside
radius (or/od)")
assert(all_positive([tooth_angle]) && tooth_angle<360*(n-1)/2/n,
str("tooth angle must be between 0 and ",360*(n-1)/2/n," for spline with
",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define both
chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value") ;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized tooth
height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going around
the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2), valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts, reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true, col_wrap=true,
row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the theta
for the chamfer “shoulder” point would be proportional to the chamfer but
it produces a slight error. It is barely noticeable but gets more blatant
at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) + phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) && tooth_angle<360*(n-1)/2/n,
str("tooth angle must be between 0 and ",360*(n-1)/2/n," for spline with
",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define both
chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value") ;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized tooth
height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going around
the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2), valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts, reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true, col_wrap=true,
row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the theta
for the chamfer “shoulder” point would be proportional to the chamfer but
it produces a slight error. It is barely noticeable but gets more blatant
at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
this is the final version (attached is the scad file)
[image: Screenshot 2024-11-07 at 10.26.12 AM.png]
On Thu, 7 Nov 2024 at 09:54, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) &&
tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
",360*(n-1)/2/n," for spline with ",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define both
chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value") ;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized tooth
height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going around
the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2),
valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts, reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
col_wrap=true, row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the
theta for the chamfer “shoulder” point would be proportional to the chamfer
but it produces a slight error. It is barely noticeable but gets more
blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
very nice! Thank you for sharing ;-)
On Wed, Nov 6, 2024 at 11:59 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
this is the final version (attached is the scad file)
[image: Screenshot 2024-11-07 at 10.26.12 AM.png]
On Thu, 7 Nov 2024 at 09:54, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I don't think the straight projection on cylinder will work.
The only way I think this can work is if you project using vectors
considering outer race and inner race, projecting outwards and inwards
respectively on outer and inner cylinder.
picture below can make this clear.
magenta lines are the vectors
[image: Screenshot 2024-11-07 at 9.49.27 AM.png]
[image: Screenshot 2024-11-07 at 9.53.29 AM.png]
On Thu, 7 Nov, 2024, 8:12 am Adrian Mariano via Discuss, <
discuss@lists.openscad.org> wrote:
Bob, I did I think exactly the same thing in my code and didn't notice
anything, but now that you mention it, doing chamfers on an angular basis
is of course not going to match doing them on a linear basis. So that
means the geometry changes a bit if you change the chamfer size. This
isn't necessarily catastrophic, but is a little unexpected, I suppose.
Generally speaking you can't mate two parts produced with different chamfer
size anyway, so I'm not sure this is crucial to get right. But in order to
get it right, I think both thetaCA2 and phiCA are going to need to be
computed with trig---either that or there's some complicated way of
computing just one. The question is whether these two parameters can be
computed independently or are they related in some complicated way.
Treated as a 2d problem you are trying to get the angle that corresponds to
a fraction of a chord of the circle, which is a reasonably straight forward
triangle calculation. I got atan(chamfer*tan(angle)) where angle is
180/tooth_count for the ridge chamfer. But the chamfered one still doesn't
align with the unchamfered. For example:
[image: image.png]
Yellow is unchamfered. Blue has huge chamfer applied only at ridge (and
slightly larger radius so we can see it clearly). And we see that the
angle has changed. I actually got less error with the original
calculation, but that might be because I didn't correct the phi angle only
the theta angle. (Or maybe I botched the trig.) So I tried computing a
correction for phi and got ridge_angle-atan(ridge_angle -
chamfer*(tan(ridge_angle)-tan(valley_angle))), but still things don't line
up correctly. (And the horizontal correction is still worse than not,
which makes me wonder if the horizontal correction needs to take into
account the vertical position of the chamfer somehow.) Doing the phi
correction alone actually is an improvement over no correction.
Here's my current code (without any chamfer corrections). It does
rounding and skew teeth.
module hirth(n, ir, or, id, od, tooth_angle=60, cone_angle=0, chamfer,
rounding, base=1, crop=false,skew=0, rot=false, orient,anchor,spin)
{
ir = get_radius(r=ir,d=id);
or = get_radius(r=or,d=od);
dummy = assert(all_positive([ir]), "ir/id must be a positive value")
assert(all_positive([or]), "or/od must be a positive value")
assert(is_int(n) && n>1, "n must be an integer larger than 1")
assert(is_finite(skew) && abs(skew)<=1, "skew must be a number
between -1 and 1")
assert(ir<or, "inside radius (ir/id) must be smaller than
outside radius (or/od)")
assert(all_positive([tooth_angle]) &&
tooth_angle<360*(n-1)/2/n, str("tooth angle must be between 0 and
",360*(n-1)/2/n," for spline with ",n," teeth."))
assert(num_defined([chamfer,rounding]) <=1, "Cannot define
both chamfer and rounding")
assert(is_undef(chamfer) || all_nonnegative([chamfer]) &&
chamfer<1/2, "chamfer must be a non-negative value smaller than 1/2")
assert(is_undef(rounding) || all_nonnegative([rounding]) &&
rounding<1/2, "rounding must be a non-negative value smaller than 1/2")
assert(all_positive([base]), "base must be a positive value") ;
tooth_height = sin(180/n) / tan(tooth_angle/2); // Normalized
tooth height
cone_height = -tan(cone_angle); // Normalized
height change corresponding to the cone angle
ridge_angle = atan(tooth_height/2 + cone_height);
valley_angle = atan(-tooth_height/2 + cone_height);
angle = 180/n; // Half the angle occupied by each tooth going
around the circle
factor = crop ? 3 : 1; // Make it oversized when crop is true
profile = is_undef(rounding) || rounding==0 ?
let(
chamfer=default(chamfer,0),
vchamf = chamfer*(ridge_angle-valley_angle),
pts = [
[-angle*(1-chamfer/2),
valley_angle+vchamf/2],
[-anglechamfer, ridge_angle-vchamf]
],
full = deduplicate(concat(pts, reverse(xflip(pts))))
)
back(valley_angle,
skew(sxy=skewangle/(ridge_angle-valley_angle),fwd(valley_angle,full)))
: let(
vround=rounding*(ridge_angle-valley_angle),
profpts = [
[ -angle, valley_angle+vround/2],
[ -angle*(1-rounding/2),
valley_angle+vround/2],
[ -anglerounding, ridge_angle-vround],
],
segs = max(16,segs(orrounding)),
full = concat(profpts, reverse(xflip(profpts))),
skewed = back(valley_angle,
skew(sxy=skew*angle/(ridge_angle-valley_angle),fwd(valley_angle,full))),
// Using computed values for the joints
lead to round-off error issues
joints = [(skewed[1]-skewed[0]).x,
(skewed[3]-skewed[2]).x/2,
(skewed[3]-skewed[2]).x/2,(skewed[5]-skewed[4]).x ],
roundpts = round_corners(skewed, joint=joints,
closed=false,$fn=segs)
)
roundpts;
// project spherical coordinate point onto cylinder of radius r
cyl_proj = function (r,theta_phi)
[for(pt=theta_phi)
let(xyz = spherical_to_xyz(1,pt[0], 90-pt[1]))
r * xyz / norm(point2d(xyz))];
bottom =
min([tan(valley_angle)ir,tan(valley_angle)or])-base-cone_heightir;
safebottom =
min([tan(valley_angle)ir/factor,tan(valley_angle)orfactor])-base-(crop?1:0)-cone_heightir;
ang_ofs = !rot ? -skewangle
: n%2==0 ? -(angle-skewangle) - skewangle
: -angle*(2-skew)-skewangle;
topinner = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(ir/factor,profile))]);
topouter = down(cone_heightir,[for(ang=lerpn(0,360,n,endpoint=false))
each
zrot(ang+ang_ofs,cyl_proj(factoror,profile))]);
botinner = [for(val=topinner) [val.x,val.y,safebottom]];
botouter = [for(val=topouter) [val.x,val.y,safebottom]];
vert = [topouter, topinner, botinner, botouter];
anchors = [
named_anchor("teeth_bot", [0,0,bottom], DOWN)
];
attachable(anchor=anchor,spin=spin,orient=orient, r=or,
h=-2*bottom,anchors=anchors){
intersection(){
vnf_polyhedron(vnf_vertex_array(vert, reverse=true,
col_wrap=true, row_wrap=true),convexity=min(10,n));
if (crop)
zmove(bottom)tube(or=or,ir=ir,height=4*or,anchor=BOT,$fa=1,$fs=1);
}
children();
}
}
On Wed, Nov 6, 2024 at 7:55 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I have established that there is an error in the code fragment. The line
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
Is where the error lies. What should it be? I was assuming that the
theta for the chamfer “shoulder” point would be proportional to the chamfer
but it produces a slight error. It is barely noticeable but gets more
blatant at low tooth counts and high conic.
Anyone see what it should be? I’m guessing there is some trig
functions involved,but ...
-Bob
On Nov 5, 2024, at 10:29, Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
Here is just a code fragment but it gets the point across.
IR = _ir(hs);
OR = _or(hs) / cos(180/_n(hs)); // OR is the radius of the
circumscribing polygon of N
// Ridge Chamfer
thetaCA2 = _toothAngle(hs) * _chamfer(hs)/200;
phiCA = (_grooveAngle(hs) -_ridgeAngle(hs)) * _chamfer(hs)/100;
function profileToooth(r) =
[spherical2_to_xyz(r, thetaCA2, _ridgeAngle(hs) +
phiCA),
spherical2_to_xyz(r, _toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, -_toothAngle(hs)/2, _grooveAngle(hs)),
spherical2_to_xyz(r, - thetaCA2, _ridgeAngle(hs) +
phiCA)
];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org