Creating inner bevel
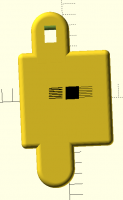
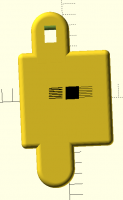
I am trying to create the following part but I am stuck on how you would create the inner bevels. Any suggestions?
The first pic is what I am trying to make.
You're missing your pic.
From: mzimbaro--- via Discuss [mailto:discuss@lists.openscad.org]
Sent: Wed, 14 Aug 2024 23:50
To: discuss@lists.openscad.org
Cc: mzimbaro@gmail.com
Subject: [OpenSCAD] Creating inner bevel
I am trying to create the following part but I am stuck on how you would create the inner bevels.
Any suggestions?
The first pic is what I am trying to make.
mzimbaro--- via Discuss [mailto:discuss@lists.openscad.org] wrote:
I am trying to create the following part but I am stuck on how you would create the inner bevels. Any suggestions?
I can't see the picture either.
The way I do this is to make a pointy end on a cylinder:
module gcp_endmill_v(es_v_angle, es_diameter) {
union(){
cylinder(r1=0, r2=(es_diameter / 2), h=((es_diameter / 2) / tan((es_v_angle / 2))), center=false);
translate([0, 0, ((es_diameter / 2) / tan((es_v_angle / 2)))]){
cylinder(r1=(es_diameter / 2), r2=(es_diameter / 2), h=((es_diameter / 2) / tan((es_v_angle / 2))), center=false);
}
}
}
and then position it along the perimeter and hull() them and then subtract that from the part.
That code is copied from
https://www.blockscad3d.com/community/projects/1430644
which in turn was used in:
https://github.com/WillAdams/gcodepreview
which while it uses Guenther Soehler's nifty OpenPythonSCAD internally is still mostly plain OpenSCAD code.
William
no idea of your the intenal shape, but you can use minkowski and a cone
minkowski(){
linear_extrude(10)
difference(){
translate([-10,-10,0]) // make hollow shape
square(100);
square(50);
}
cylinder(d1=10,d2=0,h=5); //cone
}
and remove the parts you don't want, resize if needed, etc, but it gives
a bevel around any polygon, afaik
On 14/08/2024 14:49, mzimbaro--- via Discuss wrote:
I am trying to create the following part but I am stuck on how you
would create the inner bevels. Any suggestions?
The first pic is what I am trying to make.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
For some reason it wouldn’t accept the pictures. Trying again.
If it is a shape with rounded chamfers that you want, like you show
below, then again Minkowski, but with a sphere. draw the shape smaller
by the radius of the sphere , holes, bigger by radius all around edge.
e.g., if it was a 50mm square, and 5mm thick, sphere would be d=5, and
square would be 2.5mm less on each side.
d=5; // plate thickness, and diameter of rounding
$fn=100;
// overall width of 'square' =50, hole = 10
minkowski (){
linear_extrude(0.0001){
difference(){
square([50-d,50-d]);
translate([15,15])
square([10+d,10+d]);
}
}
sphere(d=d);
}
On 15/08/2024 19:06, mzimbaro--- via Discuss wrote:
For some reason it wouldn’t accept the pictures. Trying again.
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
Thank you. I think I can make this work like you suggested. Thank you everyone for the suggestions.
It's definitely a work in progress but it is getting there.
[image: image.png]
On Thu, Aug 15, 2024 at 4:34 PM mzimbaro--- via Discuss <
discuss@lists.openscad.org> wrote:
Thank you. I think I can make this work like you suggested. Thank you
everyone for the suggestions.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
The trick to getting those inner corners is that the minkowki'd shape should have rounded inner-corners. If you start from 2d, it's easy to get those (and compensate for the added width from minkowski at the same time) by offsetting your original shape inward by the same radius. Example:
$fs = .2;
$fa = 2;
thickness = 10.0001;
radius = 5;
module shape() difference() {
union() {
square([100, 50], center = true);
square([50, 100], center = true);
}
square(20, center = true);
}
minkowski() {
linear_extrude(thickness - radius * 2, center = true) offset(-radius) shape();
sphere(radius);
}
If you ALSO want the sharpest part of those corners to be rounded like the photo, just offset it outward a little first. The back-and-forth offsetting technique is great for rounding internal and external corners (depending on the order) in 2d shapes. Example:
$fs = .2;
$fa = 2;
thickness = 10.0001;
radius = 5;
corner = 5;
module shape() difference() {
union() {
square([100, 50], center = true);
square([50, 100], center = true);
}
square(20, center = true);
}
minkowski() {
linear_extrude(thickness - radius * 2, center = true) offset(-radius - corner) offset(corner) shape();
sphere(radius);
}
On Aug 15, 2024, at 15:11, Michael Zimbaro via Discuss discuss@lists.openscad.org wrote:
It's definitely a work in progress but it is getting there.
<image.png>
On Thu, Aug 15, 2024 at 4:34 PM mzimbaro--- via Discuss discuss@lists.openscad.org wrote:
Thank you. I think I can make this work like you suggested. Thank you everyone for the suggestions.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
There has been a lot of detailed discussion, but little in the way of general discussion of the problem.
There are three basic approaches:
Create a 2D shape with holes, extrude it, and somehow (probably with Minkowski) round the corners.
Create a 3D shape, and a shape that you want removed, and difference the two.
Create the entire shape as a polyhedron, with the rounding designed in.
Minkowski can be really slow, so I generally don’t consider it. Also, it might be tricky to restrict its effect to the edges that you want rounded.
Creating a polyhedron is very very powerful and can be very very hard. I think BOSL2 might have the tools required to create a polyhedron like this, but I’m not familiar enough to be sure. Maybe Adrian can chime in there.
I would personally think in terms of the second option, subtracting the unwanted shape from the original shape.
Constructing the negative shape can be complex, but is generally straightforward even if tedious. For your oval slots, start with two cylinders joined by a cube.
I’m on my iPad so can’t experiment, but something like
difference() {
cube([50,50,10], center=true);
translate([-10,0,0]) cylinder(h=11, d=10, center=true);
translate([10,0,0]) cylinder(h=11, d=10, center=true);
cube([20,10,11], center=true);
}
That gets you a straight-sided slot. Sculpt it as desired by subtracting stuff from the negative piece. Note, for instance, that a cylinder is a rotationally-extruded square, so if you want round edges at the ends you might take a square, subtract a circle along one edge, and rotationally extrude that. Similarly, the cube in the middle is an extruded square, so take a square, subtract circles on each side, and extrude that. However you construct it, when you have your negative “die”, subtract it from the main object. Always remember to make the negative object a little thicker than the original, so that it protrudes from both sides.
If there is interest, I’ll write up a demo snippet in a few days when I get back to my desktop computer.