Ronaldo wrote

No doubt that this can be easily done. I remember an older thread, where you
showed it. But how would you automatically weave in such a patch into a
sweep or polyhedron that coats a larger structure like a roundedCube? Wasn't
that one the problems?
I didn't show it in my code, but it is straightforward if you have a quad
patch (which is squashed at one end).

--
Sent from: http://forum.openscad.org/

Following that line of thought, here is a rectangular patch to provide a
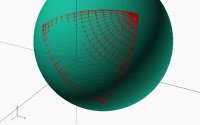
curvature continuity in rounding a corner of a cube.

[image: cornerRoundingI (1).PNG]
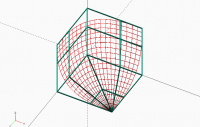
The following image shows the mesh of control points (CPs) compared with
with the patch itself.

[image: cornerRounding-CP.PNG]

As can be seen, all CPs rest on the faces of the cube in an array where one
full row of the mesh is collapsed to a point. Some intermediate rows and
columns of the mesh are movable by changing a shape parameter, others CPs
have immutable positions. The mesh of CPs of a corner were computed by the
following code:

function cornerPatchCP(P0,d,r0=0.5) =
let( P1 = P0+d*[1,0,0],
P2 = P0+d*[0,1,0],
P3 = P0+d*[0,0,1] )
[ [for(j=[0:4]) P1+P2],                                  // i=0
let(p0=P1+(1-r0)P2,p1=(P1+P2)(1-r0),p2=P1*(1-r0)+P2) // i=1
[p0,p0+r0*(p1-p0),p1,p2+r0*(p1-p2),p2],
let(p0=P1,p1=P0,p2=P2)                                // i=2
[p0,p0+r0*(p1-p0),p1,p2+r0*(p1-p2),p2],
let(p0=P1+(1-r0)P3,p1=(1-r0)P3,p2=P2+(1-r0)P3)      // i=3
[p0,p0+r0(p1-p0),p1,p2+r0(p1-p2),p2],
let(p0=P1+P3,p1=P3,p2=P2+P3)                          // i=4
[p0,p0+r0(p1-p0),p1,p2+r0*(p1-p2),p2] ];

Although it is an awkward code, it was easier to be written following the
continuity conditions. The arguments of this function are:

P0 - the coordinates of the corner
d  - the extent of cube corner that will be rounded
r0 - a shape parameter equivalent to the shape parameter of the degree 4
curves with curvature continuity

evaluating BPatchPoint(CPs,u,v) for various values of u and v in the
interval [0,1] and draw isoparametric lines or build a mesh for a
polyhedron call.

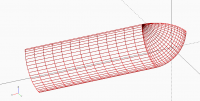
I don't like this solution. The collapse of one CP matrix row creates an
inconvenient asymmetry that can be observed by comparing the corner
rounding surface for r0 = 0.073 with the surface of a sphere:

[image: cornerRounding-sphere.PNG]

The image suggests that we have just one symmetry axis instead of 3 as
would be desirable.

Besides, a regular sample of parameters to compute points on the surface
are very irregular with a high concentration of points in the neighborhood
of the point the row was collapsed. That is a reason to pursuit a solution
based on Bezier triangular patches.

The corner surface described above has 25 CPs and a total degree of 8. My
first glance on that indicates that a degree 4 and degree 5 Bezier
triangular patch have not enough degree of freedom to accommodate the
curvature continuity conditions. Possibly a degree 6 triangular patch, with
28 CPs, will have room to satisfy all needed conditions. That will be my
next investigation.

Parkinbot rudolf@digitaldocument.de wrote:

I have solved this problem before and reported here. My lazyUnion function
is able to not only union closed manifold but stitch patches. It is
irrelevant for that module whether the patches are manifold or not. The
only condition is that each element of the incoming list is in a polyhedron
data format. And to generate a polyhedron data format for a matrix of
points (a regular mesh) or even a triangular patch is an easy task. To have
a manifold at the end is user responsability. To get it we need that the
points on the border of a patch match the points on border of a patch it
should join to and that the whole model is watertight.

Ronaldo wrote

Good point and strategy.
That was actually the solution I showed in
http://forum.openscad.org/Rounded-Polygon-tp21897p25905.html where I did a
sweep to create a corner and hulled over 8 instances of this corner.
And it wasn't as fast as the full sweep() (30s vs. 5s), but that was (as I
started to remember), because I had used a for-loop. And a for loop always
implies a union.
I just tried a run for which I put each corner as an explicite instance into
the hull body. It looks like the compile time is indeed even faster than a
full sweep (1s only). This seems to shout for a hull_for() operator that
behaves similar like the intersection_for.

Anyway, "fast" is of course always relative, because any further Boolean
operation will take its time with these vertex monsters.

--
Sent from: http://forum.openscad.org/

Parkinbot wrote

I have not yet had the time to go over what you guys have done, but I will
get to it in a few days.

What would hull_for() do?  And is the real answer not another special
command but rather a way of passing the output of a for command as a set of
children to a calling module?  Because it seems like there are multiple
occasions where you'd like to be able to generate a set of objects with
for() and then pass them to another module that operates on them
individually.  Iff a non-unioning for() command existed then it could
replace intersection_for and would have applications in a variety of places,
I think.  Is this a simpler concept than the idea of generically being able
to return multiple children from a module?

--
Sent from: http://forum.openscad.org/

There is already a PR for a non-union option for for() as part of a built
in sweep recently. It would make intersection_for() redundant as well I
think.

On Sat, 23 Mar 2019 at 23:01, adrianv avm4@cornell.edu wrote:

adrianv wrote

This is correct. And it has been discussed several times before. I think a
practical solution would be to introduce an ungroup() operator that cancels
out a following group(){} clause in the csg file, which implicitly forces a
union.

hull() for(i=[10,20]) cube(i);

translates into the CSG tree:

hull() {
group() {
cube(size = [10, 10, 10], center = false);
cube(size = [20, 20, 20], center = false);
}
}

If you edit the CSG file to

hull() {
cube(size = [10, 10, 10], center = false);
cube(size = [20, 20, 20], center = false);
}

you obviously get the desired result. Therefore

hull() ungroup() for(i=[10,20]) cube(i);

would translate into

hull() {
ungroup{
group() {
cube(size = [10, 10, 10], center = false);
cube(size = [20, 20, 20], center = false);
}
}
}

and ungroup() would inhibit the immediately following group() clause. If no
immediate group() follows, ungroup() will be ignored or cancelled out. But,
I guess there might be also semantical implications.

@thehans, what do you think?

--
Sent from: http://forum.openscad.org/

Somehow this PR gets around the problem with hull() for( ..., union=false).
See https://github.com/openscad/openscad/pull/2796#issuecomment-466836941

On Sun, 24 Mar 2019 at 00:50, Torsten Paul Torsten.Paul@gmx.de wrote: