Em sex, 29 de mar de 2019 às 17:44, adrianv avm4@cornell.edu escreveu:

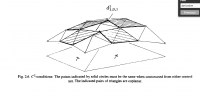
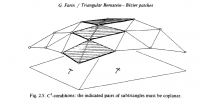
The C1 continuity (first derivative) between two adjacent triangular
patches involves the co-planarity of some triangle pairs adjacent to the
common border (see fig. 1). It is in some sense an extension of the
condition that holds for curves. The C2 continuity (second order) requires
the coindicence of some points extending from some triangles in a second
row away from the common border (see fig. 2). The figures were taken from
Farin's paper found at
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.413.7346&rep=rep1&type=pdf.
Although this is the main reference on the subject, its nomenclature is
hard to follow. I have tried without success, to express by triangular
patches the cylindrical surface of an edge rounded with the degree 4 curve.
That would help me to try meeting the necessary C2 continuity.

So this raises the questions:  Is the code correct?  Is it possible to match

This depends on what you mean by correct. I haven't seen nothing wrong with
your functions.
I still believe we could achieve the necessary C2 conditions with
triangular patches with even degree. If the 4x4 rectangular patch I built
really matches the conditions (and I am still unsure about it), then at
least a degree 8=4+4 triangular patch will do it.

Yes, possibly with a higher degree representation.

// given p, the Bezier CP of an arc of degree len(p),
// find the control points of the same arc expressed as a curve of degree
len(p)+n

function BzDegreeElevation(p, n) =
n==0 ? p :
let(q = [ p[0],
for(i=[1:len(p)-1], u = i/len(p))
u*p[i-1] + (1-u)*p[i] ,
p[len(p)-1] ] )
BzDegreeElevation  (q, n-1);

Ronaldo wrote

My patch is failing C1 even though it appears to me that I meet the
coplanarity condition for the triangles adjacent to the edge.  What is
wrong?

I have not been successful thus far at deciphering the C2 condition from the
paper.

I did confirm that my patch edges matches the shape of the 1d curve I
previously produced with the order 4 bezier.

--
Sent from: http://forum.openscad.org/

adrianv avm4@cornell.edu wrote:

Thank you for that reference: a very useful procedure.

I am also surprised that the coplanarity condition is not enough to a C1
joint. I guess I missed something from the references and that something
else is needed. I was not successful in my attempts to model a C2 or even a
C1 corner with degree 6 tripatches. However I got a tripatch model for the
cylindrical shape of the edges.

It is clear that the coplanarity condition is not preserved when we promote
a degree elevation of your degree 4 model. When we apply the degree
elevation of 1 degree to your model, the middle triangle of the border is
no longer orthogonal to the edge curve plane.

[image: DegreeElevationTo5.PNG]

To get the degree elevation I use the following function:

// find the representation of a degree n tripatch p as a degree n+m tripatch
function triPatchDegreeElevation(p, m) =
m==0? p:
let( n = len(p),
q = [ p[0],
for(i=[1:n-1], u = 1-i/n )
[ up[i][0] + (1-u)p[i-1][0],
for(j=[1:1:i-1], v = j/i )
(1-u)vp[i-1][j-1] +  (1-u)(1-v)p[i-1][j] +
up[i][j],
up[i][i] + (1-u)p[i-1][i-1]
],
[ p[n-1][0],
for(j=[1:1:n-1], v = j/n ) vp[n-1][j-1] + (1-v)*p[n-1][j],
p[n-1][n-1]
]
] )
triPatchDegreeElevation(q, m-1);

Note that this function supposes the input tripatch p is a triangular
matrix bellow the diagonal and not above as you defined in your codes.

The cylindrical shape of a rounded edge (a sweep of the degree 4 border
curve) may be modeled by:

function cylindricalPatchCP(p0, p1, p2, d, r0) =
let(  cv = curveG2CP([p0,p1,p2],r0),
bs = BzSubdiv(cv,1/2) )
[ [bs[4]+d],
[ bs[3]+3d/4, bs[5]+3d/4 ],
[ bs[2]+d/2, 2*(bs[4]+d/2)-(bs[2]+bs[6]+d)/2 , bs[6]+d/2 ],
[ bs[1]+d/4, (cv[1]+cv[2])/2+d/4, (cv[2]+cv[3])/2+d/4, bs[7]+d/4 ],
cv
];

// our well known degree 4 curve

function curveG2CP(p,r0=0.5) =
[ p[0], p[0]+r0*(p[1]-p[0]), p[1], p[2]+r0*(p[1]-p[2]), p[2] ];

// Bezier subdivision of CP p

function BzSubdiv(p,u) =
len(p) == 2 ? [p[0], (1-u)p[0]+up[1], p[1]] :
[ p[0],
each BzSubdiv([for(i=[0:len(p)-2]) (1-u)p[i]+up[i+1]],u),
p[len(p)-1] ];

That patch makes a clear C1 joint with its mirror image along axis x. This
two patches satisfy the planarity condition at the common border even with
a degree elevation.

Taking all this in consideration, my next attempt will be to find a model
such that both itself and its 1 degree elevation satisfy the condition of
orthogonality of the border triangles and the plane of border curve.

I forgot to mention: the parameter d in cylindricalPatchCP() should be
[0,0,0] to get the cylindrical shape. Parameter d deforms the shape without
changing its border derivatives.

Wrong explanation!

In this version of cylindricalPatchCP(), p0, p1 and p2 are the three points
defining the degree 4 border of the patch. The parameter d is the tip of
the tripatch opposed to that border. A typical call would be:

cylCP  = cylindricalPatchCP([10,0,10], [10,0,0], [10,10,0], [30,0,0], r0);

Em sex, 5 de abr de 2019 às 16:36, Ronaldo Persiano rcmpersiano@gmail.com
escreveu:

I am also surprised that the coplanarity condition is not enough to a C1

I understand now what was my misunderstanding of the coplanarity condition
for C1 joints. The condition is valid for the graph of real-valued
polynomials and not for muiti-valued polynomials as the tripatches. Both
references we got are concerned with interpolation problems of real-valued
data. In this case, the first two coordinates of the graph have very
specific position depending just on the triangle domain and the polynomial
degree. Although the graph may be regarded as a surface patch, the specific
positions of the projection of the CP on the xy plane does mater.

To get a C1 condition valid for three-variate polynomials we will need to
verify the coplanarity condition for each coordinate polynomial. Taking
adrian model degree 4 patch P as an example, I graphed the three
coordinates of it:

graph(revert(P), [0,0,0], [10,0,0], [0,10,0],[0,2,0], 0.05);
mirror([0,1,0]) graph(revert(P), [0,0,0], [10,0,0], [0,10,0],[0,2,0], 0.05);
translate([7,7,0]) scale([1,1,0.01]) text("X", size=1);

translate([10,0,0]){
graph(revert(P), [0,0,0], [10,0,0], [0,10,0],[2,0,0], 0.05);
mirror([0,1,0]) graph(revert(P), [0,0,0], [10,0,0], [0,10,0],[2,0,0], 0.05);
translate([7,7,0]) scale([1,1,0.01]) text("Y", size=1);
}

translate([20,0,0]){
graph(revert(P), [0,0,0], [10,0,0], [0,10,0],[0,0,2], 0.05);
mirror([0,1,0]) graph(revert(P), [0,0,0], [10,0,0], [0,10,0],[0,0,2], 0.05);
translate([7,7,0]) scale([1,1,0.01]) text("Z", size=1);
}

module graph(p, P0, P1, P2, d=[1,0,0], w) {
n = len(p);
base = [ [P0],  for(i=[1:n-1]) [for(j=[0:i]) (1-i/n)P0 + i/n(
(1-j/i)P1 + j/iP2) ]  ];
tri_grid(base,w);
graph = [for(i=[0:n-1]) [for(j=[0:i]) [base[i][j][0], base[i][j][1],
p[i][j]*d ] ] ];
translate([0,0,1])  color("red") tri_grid(graph,w);
}

module tri_grid(p, w=0.05) {
n = len(p);
for(i=[0:n-2]) for(j=[1:n-i-1]) line([p[n-i-1][j], p[n-i-1][j-1]], w=w);
for(j=[0:n-2]) for(i=[0:n-j-2]) line([p[n-i-1][j], p[n-i-2][j]],  w=w);
for(k=[0:n-2]) for(j=[1:n-k-1]) line([p[j+k][j],  p[j+k-1][j-1]], w=w);
}

function revert(p) = [for(i=[len(p)-1:-1:0]) p[i]];

The revert is needed due to the order adrian defined his patches.

The image outcome of this code is:

[image: graphs.PNG]

where the grids in blue represent the specific arranges the down projection
of the graph CP should have and the grids in red show the graph of each
coordinate of adrian surface. Besides, I mirror the graphs in order to
check the C1 conditions. It is clear from the image that just the
coordinate z has a C1 joint with it mirror image. Both coordinates X and Y
fails to have C1 continuity at those joints.

Based on that considerations we could try to build a patch that meets the
C1 condition (and perhaps the C2 condition) at the joints. However, what we
really need is G1 and G2 continuity, that is a geometric differentiabilty
and not a parametric one. Hard stuff!

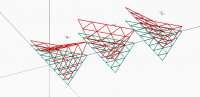
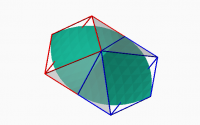
Well, I have a good news and a definitely bad one. I have found in Farin's
book ("Curves and Surfaces for CAGD") the full condition for a C1 joint
between to tripatches. Besides the co-planarity condition it is required
that any pair of CP grid triangle adjacent to the meeting border of the two
patches is an affine image of the other pairs. This affine transform should
not include any reflection, just translations, rotations and positive
scales. The following image shows the C1 joint of a degree 2 patch with its
mirror image:

[image: C1joint.PNG]

The grid in red is a mirror image of the grid in blue. The transparent
pairs of triangles satisfy the conditions of being co-planar and each one
is an affine transform of the other pair without any reflection. The joint
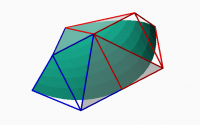
is C1. For patches of degree n the number of pairs to be considered will be
n.  Note that the condition excludes reflections as a possible affine
transform and the following image shows what happens when the affine
transform between pairs does not meet that requirement:

[image: NonC1joint.PNG]

In this example the adjacent pairs of triangles although co-planar does not
meet the affine condition restriction. The joint is clearly not C1.

I did try to apply this condition to model a rounded corner with a tripatch
and that is the bad news: it seems impossible to get, even the C1
condition, with a tripatch of any degree with all the border constraints of
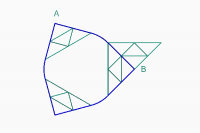
a rounded corner we need. To understand my point, consider the following
image that schematically represents a tripatch of undefined degree intended
to round a corner:

[image: SchematicCorner.PNG]

The blue lines are the patch border and some of the grid triangles near the
patch corner are represented. Besides I added the grid triangles of the
mirrored patch near patch corner B. To meet our constraints, the grid
triangles in the patch corner should be a rectangle triangle whose
hypotenuse is towards the patch center. Then, along the border AB, we need
to have the grid triangles as illustrated and no affine transform will
bring a triangle pair near A to a triangle pair near B except with some
negative scale factor (which is a reflection). So, the conditions to have a
rounded corner with curvature continuity does not allow to meet the
condition of of a C1 joint with tripatch of any degree.

We could try to model the corner with a set of tripatches like the
Clough-Tocher scheme that uses three patches, or Power-Sabin scheme with 6
tripatches. However, to get a C2 conditions between two patches of the
scheme seems to require higher degree polynomials.

The great advantage of the use of tripatch over the rectangular patch would
be the 3 symmetries that lacks in the later. It is possible to get a 3
symmetry based on the rectangular patch solution by taking the media of
sampling the three surface patches each one collapsing a row to one corner
vertex. That would be time consuming (three evaluations of a degree 8
polynomial for each sample point).

The asymmetry of the rectangular patch does not seems great enough to
justify that onus. Besides, I have confirmed that the collapsed rectangular
patch that rounds a corner is indeed curvature continuous as we had
supposed.

The condition for a C1 joint between two tripatches I have found in Farin's
book was just that small reference:

[image: C1Farin.PNG]

It is clear that if the pair is an affine map of the domain then each pair
is an affine map the other pairs. Although the text does not say it, I have
found in my experiments that the affine map in that condition cannot
include any reflection but just translations, rotations and positive
scales. The second example of my previous message corroborates that. I have
not checked whether shears are allowed.

In my examples, the pairs of triangles meeting at the border are all
coplanars. The view angle I used to generate the images might not have
being the best. You may experiment and check my conclusions playing with
the code I have used to produce the images:

// The C1 case CP
P = [ [[0,-3,0]],
[[0,-2,1.5],[-2,-2,0]],
[[2,0,0],[0,0,1.5],[-2,0,0]]
];

// The non-C1 case CP
Q = [ [[0,-3,0]],
[[2,-2,0],[-2,-2,0]],
[[2,0,0],[0,0,2],[-2,0,0]]
];

// The C1 case
translate(){
color("red")
tri_grid(P,w);
showTriPatch(P);
%showTriPatch([[P[2][0]], [P[2][1], P[1][0]]]);
%showTriPatch([[P[2][1]], [P[2][2], P[1][1]]]);
}
// Its mirror image
mirror([0,1,0]) {
color("blue")
tri_grid(P,w);
showTriPatch(P);
%showTriPatch([[P[2][0]], [P[2][1], P[1][0]]]);
%showTriPatch([[P[2][1]], [P[2][2], P[1][1]]]);
}

// The non-C1 case
translate([0,7,0]){
color("red")
tri_grid(Q,w);
showTriPatch(Q);
scale([1,1.5,1])
mirror([0,1,0]){
showTriPatch(Q);
color("blue")
tri_grid(Q,w);
}
}

// sample a tripatch with CP cp in a triangular array

function triPatchSample(cp,n) =
[for(i=[0:n-1]) [for(j=[0:i]) BtriPatchPoint(cp, (n-1-i)/(n-1), j/(n-1))
] ];

// generates the image of the surface of a tripatch p

module showTriPatch(p,n=10) {
pdat = trimesh2polyhedron(triPatchSample(p,n));
polyhedron(pdat[0],pdat[1]);
}

// computes the point in a tripatch mapped by the parameters (u,v)

function BtriPatchPoint(p,u,v) =
len(p) == 1 ? p[0][0] :
let( n  = len(p),
pu = [for(i=[0:n-2]) p[i] ],
pv = [for(i=[1:n-1]) [for(j=[0:i-1]) p[i][j] ] ],
pw = [for(i=[1:n-1]) [for(j=[1:  i]) p[i][j] ] ] )
BtriPatchPoint(upu + vpv + (1-u-v)*pw, u, v);

// generates the mesh of a triangular array of 3D points in a polyhedron
data format [verts, faces]

function trimesh2polyhedron(p,inv=false) =
let( n = len(p),
vertices = inv ?  [ for(i=[0:n-1], j=[0:i]) p[i][i-j] ]:
[ for(pt=p, q=pt) q ] ,
tris = concat(
[for(i=[1:n-1], j=[1:i])
[ j+(i+1)(i)/2, j-1+(i-1)(i)/2, j-1+(i+1)(i)/2 ]
],
n <= 2 ? [] :
[for(i=[1:n-2], j=[1:i])
[ j+(i+1)(i+2)/2, j+(i+1)(i)/2, j-1+(i+1)(i)/2 ]
]) )
[ vertices, tris ];

module line(p,closed=false,dots=false,w=0.1)
if (dots)
for(i=[0:len(p)-1])
translate(p[i]) sphere(4*w);
else
for(i=[0:len(p)-(closed? 1:2)])
hull(){ translate(p[i])  sphere(w);
translate(p[(i+1)%len(p)]) sphere(w);
}

// draw the mesh of a triangular array of points

module tri_grid(p, w=0.05) {
n = len(p);
for(i=[0:n-2]) for(j=[1:n-i-1]) line([p[n-i-1][j], p[n-i-1][j-1]], w=w);
for(j=[0:n-2]) for(i=[0:n-j-2]) line([p[n-i-1][j], p[n-i-2][j]],  w=w);
for(k=[0:n-2]) for(j=[1:n-k-1]) line([p[j+k][j],  p[j+k-1][j-1]], w=w);
}

In your second example (with the obvious C1 failure) it appears that the

Yes, they can but mapping the triangle of a patch in the triangle of the
other patch. In the code above, I changed one of the patches in order to
make this clearer. The two patches now are not the mirror image of each
other.

In musing a bit about symmetry it has occurred to me that most applications

I am not sure this makes sense. In the method of rounding a cube by hulling
spheres, would you consider a smashed sphere to have that asymmetry?
Anyway, the asymmetry of the rectangular patch with a collapsed row is very
very mild and should not have any significant effect.

It does raise the question about potential advantages of the extrusion
approach.

I agree.