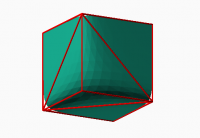
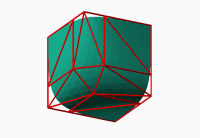
Rounded Polygon
Good solution. Your code took 16s on my machine.
--
Sent from: http://forum.openscad.org/
Ronaldo Persiano rcmpersiano@gmail.com wrote:
This is the fastest strategy I can imagine. The points sampled from the
corner patches are collected in a simple list which will be the vertices of
the fake polyhedron to be hulled. That fake polyhedron has just one face
collecting all the vertex indices. This polyhedron is defective and it is
not a manifold at all but that polyhedron is not really built, just hulled.
There is no need to resort to bogus polyhedra to follow the strategy based
on hull(). Instead, we just build a valid polyhedron for each corner and
hull() them all. Surprisingly, the preview and render times are nearly the
same as the bogus polyhedron previous code although the code is a bit more
complex.
$fn = 40; // number of points in all roundover
// 6560 vertices for $fn = 40
r0 = 0.073; // shape parameter (this value approximates a circular
arc)
r = 1.5; // rounding "radius"
s = [15,15,20]; // cube edge length
difference(){
roundedCube(s,r,r0);
rotate(90,[1,1,0])cylinder(r=2,h=40); // to check F6 validity
}
// round the edges and vertices of a block with dimensions s centered at
the origin
// s - block dimensions; may be a number or a 3d vector
// r - the extension of the edge ends that are rounded;
// equivalent to the radius of a circular rouding
// r0 - rounding shape parameter ( 0<=r0<1 )
module roundedCube(s=10, r=1, r0=0.073) {
n = $fn ? $fn: 360/$fa; // resolution
assert(0s==0 || 0s==[0,0,0], "improper size value s");
s = s[0]==undef ? [s,s,s]: s; // allow for vector and number
assert(s[0]>0 && s[1]>0 && s[2]>0, "improper cube dimensions s");
r = abs(r);
if(r==0)
cube(s, center=true);
else {
assert(2*r<=min(s), "radius r too large for the cube dimensions");
assert(r0>=0 && r0<1, "shape parameter r0 must satisfy 0<=ro<1" );
cp = cubeCornerPatchCP(-s/2,r,r0); // corner at -s/2
cp0 = PatchSample(cp,n);
pd0 = cornerPoly(cp0); // base corner patch pdat
Mx = [[-1,0,0],[0, 1,0],[0,0, 1]]; // mirror matrices
My = [[ 1,0,0],[0,-1,0],[0,0, 1]];
Mz = [[ 1,0,0],[0, 1,0],[0,0,-1]];
pd1 = [pd0];
pd2 = concat(pd1, transfPdata(Mx,pd1)); // patch mirrorings
pd4 = concat(pd2, transfPdata(My,pd2));
pd8 = concat(pd4, transfPdata(Mz,pd4));
hull()
lazyUnion(pd8); // union of the 8 corners
}
}
// unify the polyhedron data in list mPoly and call polyhedron
// assume the final polyhedron has no self-intersections
module lazyUnion(mPoly) {
// acc = accumSum(l) => acc[0]==0, acc[i]==acc[i-1]+l[i-1]
function accSum(l, res=[0]) =
len(res) == len(l) ?
res :
accSum(l, concat(res, [ res[len(res)-1]+l[len(res)-1] ] ));
verts = [for(p=mPoly) each p[0] ];
nvert = [for(p=mPoly) len(p[0]) ];
accv = accSum(nvert);
faces = [for(i=[0:len(mPoly)-1], fac=mPoly[i][1] )
[for(v=fac) v+accv[i] ] ];
polyhedron(verts, faces);
}
// transform all the vertices of each polyhedron data in list pdat by
matrix M
function transfPdata(M, pdat) = [for(pdi=pdat) [ pdi[0]*M, pdi[1] ] ];
// the polyhedron of a corner in pdat format
function cornerPoly(tpatch) =
let( n = len(tpatch) ) echo(len(tpatch),[for(i=[0:n-1]) (n-1)n/2+i ])
[ [ for(i=[0:n-1], j=[0:i]) tpatch[i][j] ], // corner vertices
// corner faces
[ for(i=[1:n-1], j=[0:i-1]) let( k = i(i+1)/2 )
each [ [ k+j, k+j-i, k+j+1 ],
if(j<i-1)[ k+j-i, k+j-i+1, k+j+1] ],
// triangular patch back faces
[for(i=[0:n-1]) i*(i+1)/2 ],
[for(i=[n-1:-1:0]) i*(i+1)/2+i ],
[for(i=[0:n-1]) (n-1)*n/2+i ],
[ 0, (n-1)*n/2, (n-1)*n/2+n-1 ]
]
];
// a point in a Bezier curve
// p - patch control points
// u - parameter value
function BezierPoint(p, u) =
(len(p) == 2)?
u*p[1] + (1-u)p[0] :
uBezierPoint([for(i=[1:len(p)-1]) p[i] ], u)
+ (1-u)*BezierPoint([for(i=[0:len(p)-2]) p[i] ], u);
// a point in a Bezier surface patch
// p - patch control points (matrix)
// u,v - parameter values
function BPatchPoint(p,u,v) =
BezierPoint(BezierPoint(p, u), v);
// sample a Bezier patch with a triangular distribuition
// cp - control points of the patch
// n - resolution
// a total of n*(n+1)/2 points are sampled
function PatchSample(cp,n) =
[for(i=[0:n-1])
[for(j=[0:i]) BPatchPoint(cp,i/(n-1),i==0? 0 : j/i) ] ];
// control points of a Bezier patch of a cube corner with curvature
continuity
// P0 - cube corner vertex
// r - the ammount of the 3 edges at the corner to be rounded
// r0 - shape parameter
function cubeCornerPatchCP(P0,r,r0=0.5) =
[for(p=curveCP([P0+[r,r,0],P0+[r,0,0],P0+[r,0,r]],r0))
curveCP([p, [p[1],p[1],p[2]], [p[1],p[0],p[2]] ], r0) ];
// control points of a degree 4 Bezier curve
// starting and ending with zero curvature
// p - corner to be rounded (list of 3 points)
// r0 - shape parameter
function curveCP(p,r0=0.5) =
[ p[0], p[0]+r0*(p[1]-p[0]), p[1], p[2]+r0*(p[1]-p[2]), p[2] ];
That code is rather fast. It takes 14s to render a rounded block with 6560
vertices.
Parkinbot, wrote:
However, there are also non-convex shapes. For them you need to do a proper
sweep, so this strategy is quite limited. In general I prefer to create
such
a patch in a way so that it can also be swept.
Yes, this technique is valid just for convex bodies. For non-convex
objects, we will have eventually to recode the computation of the patches
and it will be hard to find general solutions for corners with more than 4
incoming edges. On the other hand, I don't see how to manage the rounding
for general cases with sweeps.
I took a look at the code. Is it the case, Ronaldo, that your method is
creating a true bezier triangle, with the desired 3-axis symmetry? I read
that the bezier triangular patch can be obtained by sampling a patch in a
triangle or by collapsing two points together, but details were sparse on
what happens to the control points under these transformations.
Is the only difference between the last two versions the method of getting
the hull()? (Do they produce the same patch?)
And the sweep method Parkinbot posted is my original notion of sweeping the
bezier around the bezier, right? Do you think the curvature condition will
not hold for this approach? It seems like you could get into trouble if the
sweeping trajectory doesn't meet some kind of conditions (maybe a maximum
curvature condition?)
It seems hard to imagine generalizing continuous curvature corners beyond
solids created by linear extrusion, and for that case, it seems like the
sweep approach will be easier, no? I could imagine, instead of making
corners and hulling, making a sweep around an entire shape, though I suppose
it gets to be a lot of vertices. But this would handle concave corners, I
think? (Corners that are concave in one direction but convex in the
other.)
With the bezier patch we have 4 edges so we could round over an octahedron,
I suppose, but it not a particularly powerful generalization.
I also noticed a couple things about using bogus faces to polyhedron().
When I use the second method of creating triangles, I somtimes get "PolySet
has degenerate polygons". What does that mean? Some triangle is colinear,
or a polygon includes some colinear points? What does polyhedron do if you
give it a non-coplanar polygon?
When I tried swapping in this method into the bezier code the run time
increased from 2s to 3s for me (with
$fn=100, 40400 points in a corner patch.) I tried increasing to $fn=200,
and now 160800 points in a corner patch, and then the triangles are much
faster.
--
Sent from: http://forum.openscad.org/
adrianv avm4@cornell.edu wrote:
I took a look at the code. Is it the case, Ronaldo, that your method is
creating a true bezier triangle, with the desired 3-axis symmetry?
In that last code, I still use rectangular Bezier patches with a collapsing
row of control points so I would not expect a 3-axis symmetry. The corner
patch is the same it was used in the previous code (I have just simplified
the function that computes the patch CP).
I read that the bezier triangular patch can be obtained by sampling a
patch in a
triangle or by collapsing two points together, but details were sparse on
what happens to the control points under these transformations.
I am afraid that information is not correct.
Is the only difference between the last two versions the method of getting
the hull()? (Do they produce the same patch?)
Yes, see above.
And the sweep method Parkinbot posted is my original notion of sweeping the
bezier around the bezier, right? Do you think the curvature condition will
not hold for this approach? It seems like you could get into trouble if
the
sweeping trajectory doesn't meet some kind of conditions (maybe a maximum
curvature condition?)
Your sweep conception seems to lead to a curvature continuity in the two
axis but I have not analysed it in detail. I can not say that the Parkinbot
sweep code really follows you original conception because I have not
studied his code. Anyway, the results of a sweeping method would be
different in nature from what I have done. I would expect that the planar
face of the rounded block by the sweep method will not be a rectangle (as
in my model) but a rounded rectangle.
It seems hard to imagine generalizing continuous curvature corners beyond
solids created by linear extrusion, and for that case, it seems like the
sweep approach will be easier, no?
I would say that this last code could be easily extended to round any
convex polyhedron where just three edges meet at each vertices (like for
instance a dodecahedron). It is possible to remodel the corner patch in
order to round corners where 4 edges meet but I don't know how extend that
to more general cases where more than 4 edges meet at some corner. I don't
know how to apply the sweep method to round a dodecahedron.
I could imagine, instead of making
corners and hulling, making a sweep around an entire shape, though I
suppose
it gets to be a lot of vertices. But this would handle concave corners, I
think? (Corners that are concave in one direction but convex in the
other.)
With the bezier patch we have 4 edges so we could round over an octahedron,
I suppose, but it not a particularly powerful generalization.
Yes, see above.
I also noticed a couple things about using bogus faces to polyhedron().
When I use the second method of creating triangles, I somtimes get "PolySet
has degenerate polygons". What does that mean? Some triangle is colinear,
or a polygon includes some colinear points? What does polyhedron do if you
give it a non-coplanar polygon?
Did you get that warning with my last code? That warning usually means that
there is degenerated faces (colinear points) or a badly structured face
list or the point list has some point not referenced by any face. If some
face is non-planar, the system triangulate it in some arbitrary way. In my
last code, the corner polyhedron has 3 non-triangulated planar faces.
When I tried swapping in this method into the bezier code the run time
increased from 2s to 3s for me (with
$fn=100, 40400 points in a corner patch.) I tried increasing to $fn=200,
and now 160800 points in a corner patch, and then the triangles are much
faster.
I haven't understood what you have done here.
Ronaldo wrote
adrianv <
avm4@
> wrote:
I took a look at the code. Is it the case, Ronaldo, that your method is
creating a true bezier triangle, with the desired 3-axis symmetry?
In that last code, I still use rectangular Bezier patches with a
collapsing
row of control points so I would not expect a 3-axis symmetry. The corner
patch is the same it was used in the previous code (I have just simplified
the function that computes the patch CP).
I read that the bezier triangular patch can be obtained by sampling a
patch in a
triangle or by collapsing two points together, but details were sparse
on
what happens to the control points under these transformations.
I am afraid that information is not correct.
Are you sure? Are bezier patches or curves a different representation of
the degree n (or degree n,m) polynomial, or are there polynomials not
represented by the bezier framework? It appears just based on counting
parameters that it should be possible to get all polynomials with a bezier
representation, which would mean the claim I quoted above is true...but
perhaps not very interesting without a control point mapping.
And the sweep method Parkinbot posted is my original notion of sweeping
the
bezier around the bezier, right? Do you think the curvature condition
will
not hold for this approach? It seems like you could get into trouble if
the
sweeping trajectory doesn't meet some kind of conditions (maybe a maximum
curvature condition?)
Your sweep conception seems to lead to a curvature continuity in the two
axis but I have not analysed it in detail. I can not say that the
Parkinbot
sweep code really follows you original conception because I have not
studied his code. Anyway, the results of a sweeping method would be
different in nature from what I have done. I would expect that the planar
face of the rounded block by the sweep method will not be a rectangle (as
in my model) but a rounded rectangle.
I haven't studied his code yet either. I have to first understand the sweep
function, so it seemed like a bit more work. It seems possible that the
result would be different in nature, but I don't agree that the planar face
would be rounded. Suppose I sweep a square along a line. The result---a
standard linear extrude---is a cuboid shape with rectangular faces. If I
sweep a rounded-corner square along a line I will get a cuboid shape with
rounded edges, four rectangular faces, and then two ends whose faces are the
rounded corner square. If I sweep a rounded corner square along a rounded
corner square then (assuming the roundover doesn't dominate the square), the
square's sides will have flat sections and the sweep will convert these into
rectangular faces. I think that the resulting shape should actually be
identical to the shape produced from the bezier method except (possibly) at
the corners.
It seems hard to imagine generalizing continuous curvature corners beyond
solids created by linear extrusion, and for that case, it seems like the
sweep approach will be easier, no?
I would say that this last code could be easily extended to round any
convex polyhedron where just three edges meet at each vertices (like for
instance a dodecahedron). It is possible to remodel the corner patch in
order to round corners where 4 edges meet but I don't know how extend that
to more general cases where more than 4 edges meet at some corner. I don't
know how to apply the sweep method to round a dodecahedron.
Yes, definitely it should be straight forward to adapt your approach to a
meeting of 3 edges, and the ordinary square bezier can handle corners where
4 edges meet. I wonder if the triangular bezier can be generalized to an
n-gon bezier defined somehow on a regular n-gon?
What the sweep approach can (at least in principle) do is apply a roundover
to an (arbitrary?) shape that is generated by linear extrusion. Basically
instead of doing linear extrusion you sweep along the shape's boundary a
rounded rectangle of the appropriate dimensions to create the desired shape.
I also noticed a couple things about using bogus faces to polyhedron().
When I use the second method of creating triangles, I somtimes get
"PolySet
has degenerate polygons". What does that mean? Some triangle is
colinear,
or a polygon includes some colinear points? What does polyhedron do if
you
give it a non-coplanar polygon?
Did you get that warning with my last code? That warning usually means
that
there is degenerated faces (colinear points) or a badly structured face
list or the point list has some point not referenced by any face. If some
face is non-planar, the system triangulate it in some arbitrary way. In my
last code, the corner polyhedron has 3 non-triangulated planar faces.
No, not with the latest version of your code. With tests of the application
of hull() to bogus polyhedra.
When I tried swapping in this method into the bezier code the run time
increased from 2s to 3s for me (with
$fn=100, 40400 points in a corner patch.) I tried increasing to
$fn=200,
and now 160800 points in a corner patch, and then the triangles are much
faster.
I haven't understood what you have done here.
Your earlier version of the bezier code used the bogus polyhedron method
with one large face. I substituted small bogus triangles and it got
slightly slower when there were 40000 points in the patch. But when there
were 160000 bogus triangles were much faster than one huge bogus face.
--
Sent from: http://forum.openscad.org/
adrianv avm4@cornell.edu wrote:
I read that the bezier triangular patch can be obtained by sampling a
patch in a
triangle or by collapsing two points together, but details were sparse
on
what happens to the control points under these transformations.
I am afraid that information is not correct.
Are you sure? Are bezier patches or curves a different representation of
the degree n (or degree n,m) polynomial, or are there polynomials not
represented by the bezier framework? It appears just based on counting
parameters that it should be possible to get all polynomials with a bezier
representation, which would mean the claim I quoted above is true...but
perhaps not very interesting without a control point mapping.
Yes, I am quite sure. A rectangular Bezier patch with degrees n and m is in
a (large but incomplete) subset of all two variables polynomials of degree
(n+m). A triangular Bezier patch of degree n is really a two variable
polynomial of degree n and it has (n+1)(n+2)/2 coefficients (CPs). In our
case, degree 4, triangular patches have 15 CPs while a rectangular patch of
degree 4x4 will have 25 CPs. I guess that positioning appropriately those
25 CPs we would get any degree 4 polynomial in two variable. But the
interrelations of those CPs will be something much more complex than you
have referred. At the end, just 15 degree of freedom will remain. There is
no sampling that would exempt the fulfillment of those 10 relations.
Yes, definitely it should be straight forward to adapt your approach to a
meeting of 3 edges, and the ordinary square bezier can handle corners where
4 edges meet. I wonder if the triangular bezier can be generalized to an
n-gon bezier defined somehow on a regular n-gon?
As far as I know, there is no n-gon Bézier patch for n>4.
Did you get that warning with my last code? That warning usually means
that
there is degenerated faces (colinear points) or a badly structured face
list or the point list has some point not referenced by any face. If some
face is non-planar, the system triangulate it in some arbitrary way. In
my
last code, the corner polyhedron has 3 non-triangulated planar faces.
No, not with the latest version of your code. With tests of the
application
of hull() to bogus polyhedra.
The way I have defined that large bogus face, by taking each 3 points in
sequence as vertices of a triangle, some vertices may remain untouched by
any face when the number of vertices is not multiple of 3 and that will
generate a warning like you get.
Your earlier version of the bezier code used the bogus polyhedron method
with one large face. I substituted small bogus triangles and it got
slightly slower when there were 40000 points in the patch. But when there
were 160000 bogus triangles were much faster than one huge bogus face.
Were you comparing the running time of the bogus polyhedron process with
the Oskar Linde's hull() of points?
I have made an attempt at the triangular bezier patch. I do not know if I
have picked parameters that achieve continuous curvature, but the patch is
looking reasonable. Here is one corner, with control points displayed.
There are 3 control points that appear "free" in some sense---that is, not
falling on the edge with their value already determined to achieve the
continuous curvature edge curve.
http://forum.openscad.org/file/t2477/tribez2.png
Here's the code. It seems like computing the bezier points is kind of slow,
but I don't know if there's a more clever way to do it.
h=0.6;
corner = [0,0,0];
dx = [-1,0,0];
dy = [0,-1,0];
dz = [0,0,-1];
P1 = corner-dx-dy;
P2 = corner-dx-dz;
P3 = corner-dy-dz;
P12 = corner-dx;
P13 = corner-dy;
P23 = corner-dz;
P2face = corner-hdx-hdz;
P1face = corner - hdx-hdy;
P3face = corner-hdy-hdz;
P = [
[P1, P12+h*(P1-P12), P12, P12+h*(P2-P12), P2],
[P13 + h*(P1-P13), P1face, P2face, P23+h*(P2-P23)],
[P13, P3face, P23],
[P13 + h*(P3-P13), P23 + h*(P3-P23)],
[P3]
];
sdx=1/16;
pts = ( [for(u=[0:sdx:1])
each [for(v=[0:sdx:1-u]) tribez(P,u,v)]]);
echo(len(pts), "points");
fastpointhull(pts); //polyhedron(pts, faces=hull(pts));
function tribez(P,u,v) = len(P) == 1 ? P[0][0] :
let(
n = len(P)-1,
Pu = [for(i=[0:n-1]) select(P[i],[1:len(P[i])-1])], //
select(P[i],1,-1)],
Pv = [for(i=[0:n-1]) select(P[i],[0:len(P[i])-2])], //
select(P[i],0,len(P[i])-2)],
Pw = select(P,[1:n])
)
tribez(uPu+vPv+(1-u-v)*Pw,u,v);
%cube(size=[1,1,1]);
module fastpointhull(points){
//points = simplify3d_path(points); // colinear points are not on the
hull and generate a warning message
extra = len(points)%3;
list = concat(
[[for(i=[0:extra+2])i]],
[for(i=[extra+3:3:len(points)-3])[i,i+1,i+2]]);
hull() polyhedron(points, faces=list);
}
function select(vector,indices) = [ for (index = indices) vector[index] ];
--
Sent from: http://forum.openscad.org/
adrianv avm4@cornell.edu wrote:
I have made an attempt at the triangular bezier patch. I do not know if I
have picked parameters that achieve continuous curvature, but the patch is
looking reasonable. Here is one corner, with control points displayed.
There are 3 control points that appear "free" in some sense---that is, not
falling on the edge with their value already determined to achieve the
continuous curvature edge curve.
Nice work! I was following the same route but with degree 6 triangular
patch which is, I suppose, the minimum degree to have curvature continuity.
But I could not find a good way to compute curvature for triangular patches
to check my models. Anyway, I am afraid that the 3 CPs you consider free to
shape the surface should have precise positions to get curvature
continuity. I have drawn the triangular grid of your CPs and got the
following image with h=0.3.
As the central triangle is not coplanar with any of the corner planes I
think we would not have zero cross border second derivative at the patch
borders. Perhaps we get zero cross border curvature with h=0 but that is
too much restrictive.
My next step will be to compute the cross border curvature to check the
surface models.
Looks like a patch, but it doesn't make a smooth connection on rotation ...
translate([-1, -1])fastpointhull(pts);
rotate([0,0,90])
translate([-1, -1])fastpointhull(pts);
http://forum.openscad.org/file/t887/patch.png
--
Sent from: http://forum.openscad.org/
It's not clear to me what the constraints are for controlling the derivative
matching for the triangular patch, but yes, it appears I have with order 4
not even matched the first derivative.
So this raises the questions: Is the code correct? Is it possible to match
derivatives as desired (with a patch of sufficient order)?
Should the edges of the patch match the 4th order 1d bezier curve with the
same control points?
--
Sent from: http://forum.openscad.org/