KR
Kenneth R Sloan
Sun, Jan 22, 2023 2:14 PM
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be a
problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
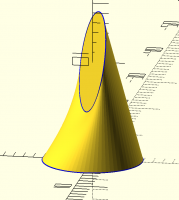
You may want to experiment with the displacement issue. The simplest test
is to use two “circles” and a range of displacements. Perfect alignment
yields a perfect cylinder. Displacement causes a crease to appear. The
limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be a
problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest test
is to use two “circles” and a range of displacements. Perfect alignment
yields a perfect cylinder. Displacement causes a crease to appear. The
limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I tried this minimum area approach and this works.
> the optimised model is really quite good.
>
>
--
-Kenneth Sloan

AM
Adrian Mariano
Sun, Jan 22, 2023 3:34 PM
Can you elaborate a bit on when or how minimizing area is expected to be
better than minimizing distance? What about the specific case of adding
an edge to a non-coplanar quadrilateral? Is there an argument in favor of
minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm more
efficient by being clever. Unfortunately, being clever rarely works in
OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
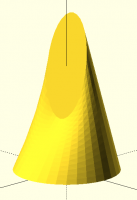
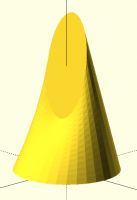
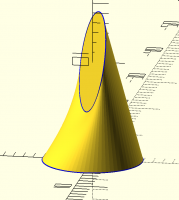
I remain baffled about the idea that displacement causes problems. I used
2 circles and every displacement produces a reasonable result. No clue
what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
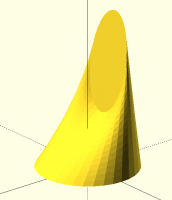
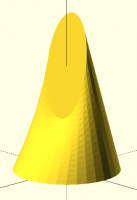
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be
a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest test
is to use two “circles” and a range of displacements. Perfect alignment
yields a perfect cylinder. Displacement causes a crease to appear. The
limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
Can you elaborate a bit on when or how minimizing area is expected to be
better than minimizing distance? What about the specific case of adding
an edge to a non-coplanar quadrilateral? Is there an argument in favor of
minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm more
efficient by being clever. Unfortunately, being clever rarely works in
OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I used
2 circles and every displacement produces a reasonable result. No clue
what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <kennethrsloan@gmail.com>
wrote:
> Excellent! Follow the references for many details on other methods and
> optimization techniques.
>
> The Fuchs, Kedem, and Uselton paper is essential. The others are either
> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
> - but please read the original (and the maybe the Sloan & Painter papers,
> if you can find them.
>
> Beware of the issue with laterally displaced slices. Scaling can also be
> a problem. Rotation is very difficult to get right. We handled it by
> creating intermediate phantom slices, but didn’t get it quite right. Note
> that we ignored rotation in the “Surfaces From Contours” paper.
>
> You may want to experiment with the displacement issue. The simplest test
> is to use two “circles” and a range of displacements. Perfect alignment
> yields a perfect cylinder. Displacement causes a crease to appear. The
> limiting case is two cones sharing a single edge.
>
> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> I tried this minimum area approach and this works.
>> the optimised model is really quite good.
>>
>>
> --
> -Kenneth Sloan
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

KR
Kenneth R Sloan
Sun, Jan 22, 2023 4:00 PM
If you don’t get 2 cones with circles displaced by a diameter, then you are
not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one curve is
very detailed in only one area. For “nornal” cases, it’s fine - which is
why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to be
better than minimizing distance? What about the specific case of adding
an edge to a non-coplanar quadrilateral? Is there an argument in favor of
minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm
more efficient by being clever. Unfortunately, being clever rarely works
in OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I used
2 circles and every displacement produces a reasonable result. No clue
what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be
a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
If you don’t get 2 cones with circles displaced by a diameter, then you are
not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one curve is
very detailed in only one area. For “nornal” cases, it’s fine - which is
why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
> Can you elaborate a bit on when or how minimizing area is expected to be
> better than minimizing distance? What about the specific case of adding
> an edge to a non-coplanar quadrilateral? Is there an argument in favor of
> minimum area vs choosing the shortest edge to add?
>
> The Fuchs, et al., paper sounds like it's trying to make the algorithm
> more efficient by being clever. Unfortunately, being clever rarely works
> in OpenSCAD code, because the overhead of the clever thing ends up being
> O(N^2). It might work for Sanjeev, since he's using Python instead of
> OpenSCAD. I'd have to spend more time studying it than seems warranted,
> since I have a working, debugged code that is fast enough for the cases on
> which I think it's relevant, namely the ones with few points. Cases with
> lots of points (smooth curves) are too slow with my code, but the results
> aren't notable. These cases seem better served by the arc length
> approach---or the arc length approach seems to produce the same result as
> the distance minimizer approach without all the computation time.
>
> I remain baffled about the idea that displacement causes problems. I used
> 2 circles and every displacement produces a reasonable result. No clue
> what you mean about 2 cones sharing an edge. Are you saying all the
> points from one circle map to a single point on the other circle? That's
> impossible in my code because it isn't an onto mapping from the source
> shape to the target shape. (Note: source shape is the one with more
> vertices, or either one in case of identical vertex count.) In fact, the
> only way the mapping can "fail" when you have the same number of points on
> each shape is by introducing a twist, which will have a larger distance, so
> it won't be the optimal solution. The only candidate mappings are twists
> of each other in this situation. It sounds like you're maybe talking
> about a very simple method that locally picks the closest point on the
> other shape, not a global optimization that minimizes the distance summed
> over all pairs of matched points, with the constraint that every point is
> in a pair.
>
> [image: image.png]
>
>
> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <kennethrsloan@gmail.com>
> wrote:
>
>> Excellent! Follow the references for many details on other methods and
>> optimization techniques.
>>
>> The Fuchs, Kedem, and Uselton paper is essential. The others are either
>> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
>> - but please read the original (and the maybe the Sloan & Painter papers,
>> if you can find them.
>>
>> Beware of the issue with laterally displaced slices. Scaling can also be
>> a problem. Rotation is very difficult to get right. We handled it by
>> creating intermediate phantom slices, but didn’t get it quite right. Note
>> that we ignored rotation in the “Surfaces From Contours” paper.
>>
>> You may want to experiment with the displacement issue. The simplest
>> test is to use two “circles” and a range of displacements. Perfect
>> alignment yields a perfect cylinder. Displacement causes a crease to
>> appear. The limiting case is two cones sharing a single edge.
>>
>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <sprabhakar2006@gmail.com>
>> wrote:
>>
>>> I tried this minimum area approach and this works.
>>> the optimised model is really quite good.
>>>
>>>
>> --
>> -Kenneth Sloan
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
--
-Kenneth Sloan

SP
Sanjeev Prabhakar
Sun, Jan 22, 2023 4:09 PM
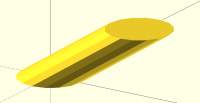
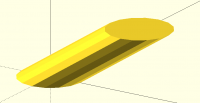
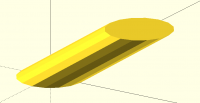
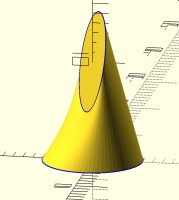
also i think if the 2 sections are not in parallel plane, minimum length
system may not work.
e.g. this is produced with area minimizing option
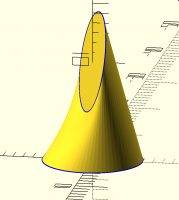
[image: Screenshot 2023-01-22 at 9.37.51 PM.png]
On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan kennethrsloan@gmail.com
wrote:
If you don’t get 2 cones with circles displaced by a diameter, then you
are not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one curve
is very detailed in only one area. For “nornal” cases, it’s fine - which
is why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to be
better than minimizing distance? What about the specific case of adding
an edge to a non-coplanar quadrilateral? Is there an argument in favor of
minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm
more efficient by being clever. Unfortunately, being clever rarely works
in OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I
used 2 circles and every displacement produces a reasonable result. No
clue what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also
be a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
also i think if the 2 sections are not in parallel plane, minimum length
system may not work.
e.g. this is produced with area minimizing option
[image: Screenshot 2023-01-22 at 9.37.51 PM.png]
On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan <kennethrsloan@gmail.com>
wrote:
> If you don’t get 2 cones with circles displaced by a diameter, then you
> are not minimizing area.
>
> O(n^2) is the best you can do for global optimization. Faster schemes
> don’t guarantee optimality.
>
> Arc length is O(n), but can lead to strange local results when one curve
> is very detailed in only one area. For “nornal” cases, it’s fine - which
> is why it’s my first choice for most practical applications.
>
> On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Can you elaborate a bit on when or how minimizing area is expected to be
>> better than minimizing distance? What about the specific case of adding
>> an edge to a non-coplanar quadrilateral? Is there an argument in favor of
>> minimum area vs choosing the shortest edge to add?
>>
>> The Fuchs, et al., paper sounds like it's trying to make the algorithm
>> more efficient by being clever. Unfortunately, being clever rarely works
>> in OpenSCAD code, because the overhead of the clever thing ends up being
>> O(N^2). It might work for Sanjeev, since he's using Python instead of
>> OpenSCAD. I'd have to spend more time studying it than seems warranted,
>> since I have a working, debugged code that is fast enough for the cases on
>> which I think it's relevant, namely the ones with few points. Cases with
>> lots of points (smooth curves) are too slow with my code, but the results
>> aren't notable. These cases seem better served by the arc length
>> approach---or the arc length approach seems to produce the same result as
>> the distance minimizer approach without all the computation time.
>>
>> I remain baffled about the idea that displacement causes problems. I
>> used 2 circles and every displacement produces a reasonable result. No
>> clue what you mean about 2 cones sharing an edge. Are you saying all the
>> points from one circle map to a single point on the other circle? That's
>> impossible in my code because it isn't an onto mapping from the source
>> shape to the target shape. (Note: source shape is the one with more
>> vertices, or either one in case of identical vertex count.) In fact, the
>> only way the mapping can "fail" when you have the same number of points on
>> each shape is by introducing a twist, which will have a larger distance, so
>> it won't be the optimal solution. The only candidate mappings are twists
>> of each other in this situation. It sounds like you're maybe talking
>> about a very simple method that locally picks the closest point on the
>> other shape, not a global optimization that minimizes the distance summed
>> over all pairs of matched points, with the constraint that every point is
>> in a pair.
>>
>> [image: image.png]
>>
>>
>> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <kennethrsloan@gmail.com>
>> wrote:
>>
>>> Excellent! Follow the references for many details on other methods and
>>> optimization techniques.
>>>
>>> The Fuchs, Kedem, and Uselton paper is essential. The others are either
>>> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
>>> - but please read the original (and the maybe the Sloan & Painter papers,
>>> if you can find them.
>>>
>>> Beware of the issue with laterally displaced slices. Scaling can also
>>> be a problem. Rotation is very difficult to get right. We handled it by
>>> creating intermediate phantom slices, but didn’t get it quite right. Note
>>> that we ignored rotation in the “Surfaces From Contours” paper.
>>>
>>> You may want to experiment with the displacement issue. The simplest
>>> test is to use two “circles” and a range of displacements. Perfect
>>> alignment yields a perfect cylinder. Displacement causes a crease to
>>> appear. The limiting case is two cones sharing a single edge.
>>>
>>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> I tried this minimum area approach and this works.
>>>> the optimised model is really quite good.
>>>>
>>>>
>>> --
>>> -Kenneth Sloan
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> --
> -Kenneth Sloan
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Sun, Jan 22, 2023 5:18 PM
Kenneth, it seems like we have a communications problem here, so let me try
to lay out my approach precisely:
I am minimizing an objective function f() over a feasible set S. So that
means looking for an item in s in S that minimizes the value f(s).
In my problem I have two contours, C1 and C2 where the vertex count of C1
is m and the vertex count of C2 is n, and m>=n. What are the members of
S? They are mappings that map the vertices from C1 to C2 while preserving
order and ensuring that the map is onto (surjective), so that every vertex
in C2 is covered by some vertex from C1. What does it mean to preserve
order? It means that if v1 and v2 are adjacent vertices in C1 then they
are either adjacent or identical when mapped to C2.
The two cones solution is not in S, because it maps a single point in C1 to
multiple points in C2. I don't consider it a valid option. Therefore it
can NEVER occur, no matter what objective function I use. Now you can
argue that my approach isn't general because I don't allow a vertex in C1
to map to two vertices in C2. But it sounds like if it prevents
pathological results such as you describe, the restriction may have
advantages.
My algorithm is O(m n^2). But I think you did not get my point. It's
easy to read about some algorithm that improves run time of some method,
maybe from O(n^2) to O(n log n). In OpenSCAD (a language without data
structures) you might find that the extra overhead of this improvement ADDS
O(n^2) in overhead so the result is that the "fast" algorithm is O(n^3 log
n), and hence is not so fast after all. Even if you only have O(n)
overhead, you're in trouble in this example, because n^2 log n is worse
than n^2.
With regard to the objective function, I'm computing the sum of m
distances. Note that in this context, I don't know how to compute area
accurately, because when a quadrilateral face is constructed, it is likely
a curved surface, so if I tried to recode this to use area I would
presumably be using approximate area based on triangles, not the real
area.
On Sun, Jan 22, 2023 at 11:01 AM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
If you don’t get 2 cones with circles displaced by a diameter, then you
are not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one curve
is very detailed in only one area. For “nornal” cases, it’s fine - which
is why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to be
better than minimizing distance? What about the specific case of adding
an edge to a non-coplanar quadrilateral? Is there an argument in favor of
minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm
more efficient by being clever. Unfortunately, being clever rarely works
in OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I
used 2 circles and every displacement produces a reasonable result. No
clue what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also
be a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
Kenneth, it seems like we have a communications problem here, so let me try
to lay out my approach precisely:
I am minimizing an objective function f() over a feasible set S. So that
means looking for an item in s in S that minimizes the value f(s).
In my problem I have two contours, C1 and C2 where the vertex count of C1
is m and the vertex count of C2 is n, and m>=n. What are the members of
S? They are mappings that map the vertices from C1 to C2 while preserving
order and ensuring that the map is onto (surjective), so that every vertex
in C2 is covered by some vertex from C1. What does it mean to preserve
order? It means that if v1 and v2 are adjacent vertices in C1 then they
are either adjacent or identical when mapped to C2.
The two cones solution is not in S, because it maps a single point in C1 to
multiple points in C2. I don't consider it a valid option. Therefore it
can NEVER occur, no matter what objective function I use. Now you can
argue that my approach isn't general because I don't allow a vertex in C1
to map to two vertices in C2. But it sounds like if it prevents
pathological results such as you describe, the restriction may have
advantages.
My algorithm is O(m n^2). But I think you did not get my point. It's
easy to read about some algorithm that improves run time of some method,
maybe from O(n^2) to O(n log n). In OpenSCAD (a language without data
structures) you might find that the extra overhead of this improvement ADDS
O(n^2) in overhead so the result is that the "fast" algorithm is O(n^3 log
n), and hence is not so fast after all. Even if you only have O(n)
overhead, you're in trouble in this example, because n^2 log n is worse
than n^2.
With regard to the objective function, I'm computing the sum of m
distances. Note that in this context, I don't know how to compute area
accurately, because when a quadrilateral face is constructed, it is likely
a curved surface, so if I tried to recode this to use area I would
presumably be using approximate area based on triangles, not the real
area.
On Sun, Jan 22, 2023 at 11:01 AM Kenneth R Sloan <kennethrsloan@gmail.com>
wrote:
> If you don’t get 2 cones with circles displaced by a diameter, then you
> are not minimizing area.
>
> O(n^2) is the best you can do for global optimization. Faster schemes
> don’t guarantee optimality.
>
> Arc length is O(n), but can lead to strange local results when one curve
> is very detailed in only one area. For “nornal” cases, it’s fine - which
> is why it’s my first choice for most practical applications.
>
> On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Can you elaborate a bit on when or how minimizing area is expected to be
>> better than minimizing distance? What about the specific case of adding
>> an edge to a non-coplanar quadrilateral? Is there an argument in favor of
>> minimum area vs choosing the shortest edge to add?
>>
>> The Fuchs, et al., paper sounds like it's trying to make the algorithm
>> more efficient by being clever. Unfortunately, being clever rarely works
>> in OpenSCAD code, because the overhead of the clever thing ends up being
>> O(N^2). It might work for Sanjeev, since he's using Python instead of
>> OpenSCAD. I'd have to spend more time studying it than seems warranted,
>> since I have a working, debugged code that is fast enough for the cases on
>> which I think it's relevant, namely the ones with few points. Cases with
>> lots of points (smooth curves) are too slow with my code, but the results
>> aren't notable. These cases seem better served by the arc length
>> approach---or the arc length approach seems to produce the same result as
>> the distance minimizer approach without all the computation time.
>>
>> I remain baffled about the idea that displacement causes problems. I
>> used 2 circles and every displacement produces a reasonable result. No
>> clue what you mean about 2 cones sharing an edge. Are you saying all the
>> points from one circle map to a single point on the other circle? That's
>> impossible in my code because it isn't an onto mapping from the source
>> shape to the target shape. (Note: source shape is the one with more
>> vertices, or either one in case of identical vertex count.) In fact, the
>> only way the mapping can "fail" when you have the same number of points on
>> each shape is by introducing a twist, which will have a larger distance, so
>> it won't be the optimal solution. The only candidate mappings are twists
>> of each other in this situation. It sounds like you're maybe talking
>> about a very simple method that locally picks the closest point on the
>> other shape, not a global optimization that minimizes the distance summed
>> over all pairs of matched points, with the constraint that every point is
>> in a pair.
>>
>> [image: image.png]
>>
>>
>> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <kennethrsloan@gmail.com>
>> wrote:
>>
>>> Excellent! Follow the references for many details on other methods and
>>> optimization techniques.
>>>
>>> The Fuchs, Kedem, and Uselton paper is essential. The others are either
>>> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
>>> - but please read the original (and the maybe the Sloan & Painter papers,
>>> if you can find them.
>>>
>>> Beware of the issue with laterally displaced slices. Scaling can also
>>> be a problem. Rotation is very difficult to get right. We handled it by
>>> creating intermediate phantom slices, but didn’t get it quite right. Note
>>> that we ignored rotation in the “Surfaces From Contours” paper.
>>>
>>> You may want to experiment with the displacement issue. The simplest
>>> test is to use two “circles” and a range of displacements. Perfect
>>> alignment yields a perfect cylinder. Displacement causes a crease to
>>> appear. The limiting case is two cones sharing a single edge.
>>>
>>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> I tried this minimum area approach and this works.
>>>> the optimised model is really quite good.
>>>>
>>>>
>>> --
>>> -Kenneth Sloan
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> --
> -Kenneth Sloan
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Sun, Jan 22, 2023 5:23 PM
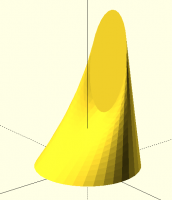
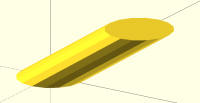
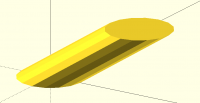
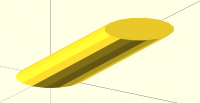
Sanjeev, I don't understand why using minimum length should be any less
robust than minimum area. I think the difference in results of the two
methods, at least in the context of my implementation, would be very
small. And it would be especially small in the case like the one you
show, where the triangles are long and thin, because in that case, length
(distance) is a good approximation for area.
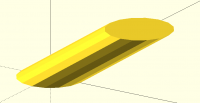
[image: image.png]
On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
also i think if the 2 sections are not in parallel plane, minimum length
system may not work.
e.g. this is produced with area minimizing option
[image: Screenshot 2023-01-22 at 9.37.51 PM.png]
On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan kennethrsloan@gmail.com
wrote:
If you don’t get 2 cones with circles displaced by a diameter, then you
are not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one curve
is very detailed in only one area. For “nornal” cases, it’s fine - which
is why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to be
better than minimizing distance? What about the specific case of adding
an edge to a non-coplanar quadrilateral? Is there an argument in favor of
minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm
more efficient by being clever. Unfortunately, being clever rarely works
in OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I
used 2 circles and every displacement produces a reasonable result. No
clue what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are
either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
version - but please read the original (and the maybe the Sloan & Painter
papers, if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also
be a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
Sanjeev, I don't understand why using minimum length should be any less
robust than minimum area. I think the difference in results of the two
methods, at least in the context of my implementation, would be very
small. And it would be *especially* small in the case like the one you
show, where the triangles are long and thin, because in that case, length
(distance) is a good approximation for area.
[image: image.png]
On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> also i think if the 2 sections are not in parallel plane, minimum length
> system may not work.
>
> e.g. this is produced with area minimizing option
> [image: Screenshot 2023-01-22 at 9.37.51 PM.png]
>
>
> On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan <kennethrsloan@gmail.com>
> wrote:
>
>> If you don’t get 2 cones with circles displaced by a diameter, then you
>> are not minimizing area.
>>
>> O(n^2) is the best you can do for global optimization. Faster schemes
>> don’t guarantee optimality.
>>
>> Arc length is O(n), but can lead to strange local results when one curve
>> is very detailed in only one area. For “nornal” cases, it’s fine - which
>> is why it’s my first choice for most practical applications.
>>
>> On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Can you elaborate a bit on when or how minimizing area is expected to be
>>> better than minimizing distance? What about the specific case of adding
>>> an edge to a non-coplanar quadrilateral? Is there an argument in favor of
>>> minimum area vs choosing the shortest edge to add?
>>>
>>> The Fuchs, et al., paper sounds like it's trying to make the algorithm
>>> more efficient by being clever. Unfortunately, being clever rarely works
>>> in OpenSCAD code, because the overhead of the clever thing ends up being
>>> O(N^2). It might work for Sanjeev, since he's using Python instead of
>>> OpenSCAD. I'd have to spend more time studying it than seems warranted,
>>> since I have a working, debugged code that is fast enough for the cases on
>>> which I think it's relevant, namely the ones with few points. Cases with
>>> lots of points (smooth curves) are too slow with my code, but the results
>>> aren't notable. These cases seem better served by the arc length
>>> approach---or the arc length approach seems to produce the same result as
>>> the distance minimizer approach without all the computation time.
>>>
>>> I remain baffled about the idea that displacement causes problems. I
>>> used 2 circles and every displacement produces a reasonable result. No
>>> clue what you mean about 2 cones sharing an edge. Are you saying all the
>>> points from one circle map to a single point on the other circle? That's
>>> impossible in my code because it isn't an onto mapping from the source
>>> shape to the target shape. (Note: source shape is the one with more
>>> vertices, or either one in case of identical vertex count.) In fact, the
>>> only way the mapping can "fail" when you have the same number of points on
>>> each shape is by introducing a twist, which will have a larger distance, so
>>> it won't be the optimal solution. The only candidate mappings are twists
>>> of each other in this situation. It sounds like you're maybe talking
>>> about a very simple method that locally picks the closest point on the
>>> other shape, not a global optimization that minimizes the distance summed
>>> over all pairs of matched points, with the constraint that every point is
>>> in a pair.
>>>
>>> [image: image.png]
>>>
>>>
>>> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <kennethrsloan@gmail.com>
>>> wrote:
>>>
>>>> Excellent! Follow the references for many details on other methods and
>>>> optimization techniques.
>>>>
>>>> The Fuchs, Kedem, and Uselton paper is essential. The others are
>>>> either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
>>>> version - but please read the original (and the maybe the Sloan & Painter
>>>> papers, if you can find them.
>>>>
>>>> Beware of the issue with laterally displaced slices. Scaling can also
>>>> be a problem. Rotation is very difficult to get right. We handled it by
>>>> creating intermediate phantom slices, but didn’t get it quite right. Note
>>>> that we ignored rotation in the “Surfaces From Contours” paper.
>>>>
>>>> You may want to experiment with the displacement issue. The simplest
>>>> test is to use two “circles” and a range of displacements. Perfect
>>>> alignment yields a perfect cylinder. Displacement causes a crease to
>>>> appear. The limiting case is two cones sharing a single edge.
>>>>
>>>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
>>>> sprabhakar2006@gmail.com> wrote:
>>>>
>>>>> I tried this minimum area approach and this works.
>>>>> the optimised model is really quite good.
>>>>>
>>>>>
>>>> --
>>>> -Kenneth Sloan
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> --
>> -Kenneth Sloan
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

NH
nop head
Sun, Jan 22, 2023 6:26 PM
If you map the points of a circle at one end to points on the other end 180
degrees further round that gives a 1:1 mapping that will make two cones
meeting at a point in between.
If you go for the nearest point with the top circle sharply inclined it the
lower points could be nearer the back of the base than the correct point
which is more distant at the back of the top.
On Sun, 22 Jan 2023 at 17:24, Adrian Mariano avm4@cornell.edu wrote:
Sanjeev, I don't understand why using minimum length should be any less
robust than minimum area. I think the difference in results of the two
methods, at least in the context of my implementation, would be very
small. And it would be especially small in the case like the one you
show, where the triangles are long and thin, because in that case, length
(distance) is a good approximation for area.
[image: image.png]
On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
also i think if the 2 sections are not in parallel plane, minimum length
system may not work.
e.g. this is produced with area minimizing option
[image: Screenshot 2023-01-22 at 9.37.51 PM.png]
On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan kennethrsloan@gmail.com
wrote:
If you don’t get 2 cones with circles displaced by a diameter, then you
are not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one curve
is very detailed in only one area. For “nornal” cases, it’s fine - which
is why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to
be better than minimizing distance? What about the specific case of
adding an edge to a non-coplanar quadrilateral? Is there an argument in
favor of minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm
more efficient by being clever. Unfortunately, being clever rarely works
in OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I
used 2 circles and every displacement produces a reasonable result. No
clue what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <
kennethrsloan@gmail.com> wrote:
Excellent! Follow the references for many details on other methods
and optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are
either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
version - but please read the original (and the maybe the Sloan & Painter
papers, if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also
be a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
If you map the points of a circle at one end to points on the other end 180
degrees further round that gives a 1:1 mapping that will make two cones
meeting at a point in between.
If you go for the nearest point with the top circle sharply inclined it the
lower points could be nearer the back of the base than the correct point
which is more distant at the back of the top.
On Sun, 22 Jan 2023 at 17:24, Adrian Mariano <avm4@cornell.edu> wrote:
> Sanjeev, I don't understand why using minimum length should be any less
> robust than minimum area. I think the difference in results of the two
> methods, at least in the context of my implementation, would be very
> small. And it would be *especially* small in the case like the one you
> show, where the triangles are long and thin, because in that case, length
> (distance) is a good approximation for area.
>
> [image: image.png]
>
>
> On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> also i think if the 2 sections are not in parallel plane, minimum length
>> system may not work.
>>
>> e.g. this is produced with area minimizing option
>> [image: Screenshot 2023-01-22 at 9.37.51 PM.png]
>>
>>
>> On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan <kennethrsloan@gmail.com>
>> wrote:
>>
>>> If you don’t get 2 cones with circles displaced by a diameter, then you
>>> are not minimizing area.
>>>
>>> O(n^2) is the best you can do for global optimization. Faster schemes
>>> don’t guarantee optimality.
>>>
>>> Arc length is O(n), but can lead to strange local results when one curve
>>> is very detailed in only one area. For “nornal” cases, it’s fine - which
>>> is why it’s my first choice for most practical applications.
>>>
>>> On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> Can you elaborate a bit on when or how minimizing area is expected to
>>>> be better than minimizing distance? What about the specific case of
>>>> adding an edge to a non-coplanar quadrilateral? Is there an argument in
>>>> favor of minimum area vs choosing the shortest edge to add?
>>>>
>>>> The Fuchs, et al., paper sounds like it's trying to make the algorithm
>>>> more efficient by being clever. Unfortunately, being clever rarely works
>>>> in OpenSCAD code, because the overhead of the clever thing ends up being
>>>> O(N^2). It might work for Sanjeev, since he's using Python instead of
>>>> OpenSCAD. I'd have to spend more time studying it than seems warranted,
>>>> since I have a working, debugged code that is fast enough for the cases on
>>>> which I think it's relevant, namely the ones with few points. Cases with
>>>> lots of points (smooth curves) are too slow with my code, but the results
>>>> aren't notable. These cases seem better served by the arc length
>>>> approach---or the arc length approach seems to produce the same result as
>>>> the distance minimizer approach without all the computation time.
>>>>
>>>> I remain baffled about the idea that displacement causes problems. I
>>>> used 2 circles and every displacement produces a reasonable result. No
>>>> clue what you mean about 2 cones sharing an edge. Are you saying all the
>>>> points from one circle map to a single point on the other circle? That's
>>>> impossible in my code because it isn't an onto mapping from the source
>>>> shape to the target shape. (Note: source shape is the one with more
>>>> vertices, or either one in case of identical vertex count.) In fact, the
>>>> only way the mapping can "fail" when you have the same number of points on
>>>> each shape is by introducing a twist, which will have a larger distance, so
>>>> it won't be the optimal solution. The only candidate mappings are twists
>>>> of each other in this situation. It sounds like you're maybe talking
>>>> about a very simple method that locally picks the closest point on the
>>>> other shape, not a global optimization that minimizes the distance summed
>>>> over all pairs of matched points, with the constraint that every point is
>>>> in a pair.
>>>>
>>>> [image: image.png]
>>>>
>>>>
>>>> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <
>>>> kennethrsloan@gmail.com> wrote:
>>>>
>>>>> Excellent! Follow the references for many details on other methods
>>>>> and optimization techniques.
>>>>>
>>>>> The Fuchs, Kedem, and Uselton paper is essential. The others are
>>>>> either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
>>>>> version - but please read the original (and the maybe the Sloan & Painter
>>>>> papers, if you can find them.
>>>>>
>>>>> Beware of the issue with laterally displaced slices. Scaling can also
>>>>> be a problem. Rotation is very difficult to get right. We handled it by
>>>>> creating intermediate phantom slices, but didn’t get it quite right. Note
>>>>> that we ignored rotation in the “Surfaces From Contours” paper.
>>>>>
>>>>> You may want to experiment with the displacement issue. The simplest
>>>>> test is to use two “circles” and a range of displacements. Perfect
>>>>> alignment yields a perfect cylinder. Displacement causes a crease to
>>>>> appear. The limiting case is two cones sharing a single edge.
>>>>>
>>>>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>
>>>>>> I tried this minimum area approach and this works.
>>>>>> the optimised model is really quite good.
>>>>>>
>>>>>>
>>>>> --
>>>>> -Kenneth Sloan
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> --
>>> -Kenneth Sloan
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Sun, Jan 22, 2023 6:36 PM
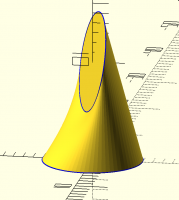
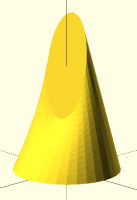
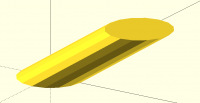
nophead, he didn't mean two cones meeting at a point. He meant two
(skewed) cones intersecting at an edge, with one cone apex on the top
circle and one cone apex on the bottom circle.
My method is global. It is not going for a single nearest point, but
minimizing the distance of all the points jointly. So the fact that there
is an obvious way to get a single point in bad correspondence doesn't show
that the full solution will actually come out that way. If you use the
arc-length approach you have to pick a starting point, and there you could
run into trouble if you don't use a global approach of some sort to do it.
Here's the case you describe, where the bottom of the ellipse is closer to
the back of the circle, and the solution is by distance minimization. That
doesn't lead it to map to the back of the circle.
[image: image.png]
On Sun, Jan 22, 2023 at 1:27 PM nop head nop.head@gmail.com wrote:
If you map the points of a circle at one end to points on the other end
180 degrees further round that gives a 1:1 mapping that will make two cones
meeting at a point in between.
If you go for the nearest point with the top circle sharply inclined it
the lower points could be nearer the back of the base than the correct
point which is more distant at the back of the top.
On Sun, 22 Jan 2023 at 17:24, Adrian Mariano avm4@cornell.edu wrote:
Sanjeev, I don't understand why using minimum length should be any less
robust than minimum area. I think the difference in results of the two
methods, at least in the context of my implementation, would be very
small. And it would be especially small in the case like the one you
show, where the triangles are long and thin, because in that case, length
(distance) is a good approximation for area.
[image: image.png]
On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
also i think if the 2 sections are not in parallel plane, minimum length
system may not work.
e.g. this is produced with area minimizing option
[image: Screenshot 2023-01-22 at 9.37.51 PM.png]
On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan kennethrsloan@gmail.com
wrote:
If you don’t get 2 cones with circles displaced by a diameter, then you
are not minimizing area.
O(n^2) is the best you can do for global optimization. Faster schemes
don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one
curve is very detailed in only one area. For “nornal” cases, it’s fine -
which is why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to
be better than minimizing distance? What about the specific case of
adding an edge to a non-coplanar quadrilateral? Is there an argument in
favor of minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the algorithm
more efficient by being clever. Unfortunately, being clever rarely works
in OpenSCAD code, because the overhead of the clever thing ends up being
O(N^2). It might work for Sanjeev, since he's using Python instead of
OpenSCAD. I'd have to spend more time studying it than seems warranted,
since I have a working, debugged code that is fast enough for the cases on
which I think it's relevant, namely the ones with few points. Cases with
lots of points (smooth curves) are too slow with my code, but the results
aren't notable. These cases seem better served by the arc length
approach---or the arc length approach seems to produce the same result as
the distance minimizer approach without all the computation time.
I remain baffled about the idea that displacement causes problems. I
used 2 circles and every displacement produces a reasonable result. No
clue what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <
kennethrsloan@gmail.com> wrote:
Excellent! Follow the references for many details on other methods
and optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are
either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
version - but please read the original (and the maybe the Sloan & Painter
papers, if you can find them.
Beware of the issue with laterally displaced slices. Scaling can
also be a problem. Rotation is very difficult to get right. We handled it
by creating intermediate phantom slices, but didn’t get it quite right.
Note that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
nophead, he didn't mean two cones meeting at a point. He meant two
(skewed) cones intersecting at an edge, with one cone apex on the top
circle and one cone apex on the bottom circle.
My method is *global*. It is not going for a single nearest point, but
minimizing the distance of all the points jointly. So the fact that there
is an obvious way to get a single point in bad correspondence doesn't show
that the full solution will actually come out that way. If you use the
arc-length approach you have to pick a starting point, and there you could
run into trouble if you don't use a global approach of some sort to do it.
Here's the case you describe, where the bottom of the ellipse is closer to
the back of the circle, and the solution is by distance minimization. That
doesn't lead it to map to the back of the circle.
[image: image.png]
On Sun, Jan 22, 2023 at 1:27 PM nop head <nop.head@gmail.com> wrote:
> If you map the points of a circle at one end to points on the other end
> 180 degrees further round that gives a 1:1 mapping that will make two cones
> meeting at a point in between.
>
> If you go for the nearest point with the top circle sharply inclined it
> the lower points could be nearer the back of the base than the correct
> point which is more distant at the back of the top.
>
> On Sun, 22 Jan 2023 at 17:24, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Sanjeev, I don't understand why using minimum length should be any less
>> robust than minimum area. I think the difference in results of the two
>> methods, at least in the context of my implementation, would be very
>> small. And it would be *especially* small in the case like the one you
>> show, where the triangles are long and thin, because in that case, length
>> (distance) is a good approximation for area.
>>
>> [image: image.png]
>>
>>
>> On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> also i think if the 2 sections are not in parallel plane, minimum length
>>> system may not work.
>>>
>>> e.g. this is produced with area minimizing option
>>> [image: Screenshot 2023-01-22 at 9.37.51 PM.png]
>>>
>>>
>>> On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan <kennethrsloan@gmail.com>
>>> wrote:
>>>
>>>> If you don’t get 2 cones with circles displaced by a diameter, then you
>>>> are not minimizing area.
>>>>
>>>> O(n^2) is the best you can do for global optimization. Faster schemes
>>>> don’t guarantee optimality.
>>>>
>>>> Arc length is O(n), but can lead to strange local results when one
>>>> curve is very detailed in only one area. For “nornal” cases, it’s fine -
>>>> which is why it’s my first choice for most practical applications.
>>>>
>>>> On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
>>>>
>>>>> Can you elaborate a bit on when or how minimizing area is expected to
>>>>> be better than minimizing distance? What about the specific case of
>>>>> adding an edge to a non-coplanar quadrilateral? Is there an argument in
>>>>> favor of minimum area vs choosing the shortest edge to add?
>>>>>
>>>>> The Fuchs, et al., paper sounds like it's trying to make the algorithm
>>>>> more efficient by being clever. Unfortunately, being clever rarely works
>>>>> in OpenSCAD code, because the overhead of the clever thing ends up being
>>>>> O(N^2). It might work for Sanjeev, since he's using Python instead of
>>>>> OpenSCAD. I'd have to spend more time studying it than seems warranted,
>>>>> since I have a working, debugged code that is fast enough for the cases on
>>>>> which I think it's relevant, namely the ones with few points. Cases with
>>>>> lots of points (smooth curves) are too slow with my code, but the results
>>>>> aren't notable. These cases seem better served by the arc length
>>>>> approach---or the arc length approach seems to produce the same result as
>>>>> the distance minimizer approach without all the computation time.
>>>>>
>>>>> I remain baffled about the idea that displacement causes problems. I
>>>>> used 2 circles and every displacement produces a reasonable result. No
>>>>> clue what you mean about 2 cones sharing an edge. Are you saying all the
>>>>> points from one circle map to a single point on the other circle? That's
>>>>> impossible in my code because it isn't an onto mapping from the source
>>>>> shape to the target shape. (Note: source shape is the one with more
>>>>> vertices, or either one in case of identical vertex count.) In fact, the
>>>>> only way the mapping can "fail" when you have the same number of points on
>>>>> each shape is by introducing a twist, which will have a larger distance, so
>>>>> it won't be the optimal solution. The only candidate mappings are twists
>>>>> of each other in this situation. It sounds like you're maybe talking
>>>>> about a very simple method that locally picks the closest point on the
>>>>> other shape, not a global optimization that minimizes the distance summed
>>>>> over all pairs of matched points, with the constraint that every point is
>>>>> in a pair.
>>>>>
>>>>> [image: image.png]
>>>>>
>>>>>
>>>>> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <
>>>>> kennethrsloan@gmail.com> wrote:
>>>>>
>>>>>> Excellent! Follow the references for many details on other methods
>>>>>> and optimization techniques.
>>>>>>
>>>>>> The Fuchs, Kedem, and Uselton paper is essential. The others are
>>>>>> either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
>>>>>> version - but please read the original (and the maybe the Sloan & Painter
>>>>>> papers, if you can find them.
>>>>>>
>>>>>> Beware of the issue with laterally displaced slices. Scaling can
>>>>>> also be a problem. Rotation is very difficult to get right. We handled it
>>>>>> by creating intermediate phantom slices, but didn’t get it quite right.
>>>>>> Note that we ignored rotation in the “Surfaces From Contours” paper.
>>>>>>
>>>>>> You may want to experiment with the displacement issue. The simplest
>>>>>> test is to use two “circles” and a range of displacements. Perfect
>>>>>> alignment yields a perfect cylinder. Displacement causes a crease to
>>>>>> appear. The limiting case is two cones sharing a single edge.
>>>>>>
>>>>>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>
>>>>>>> I tried this minimum area approach and this works.
>>>>>>> the optimised model is really quite good.
>>>>>>>
>>>>>>>
>>>>>> --
>>>>>> -Kenneth Sloan
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> --
>>>> -Kenneth Sloan
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Mon, Jan 23, 2023 1:53 AM
I think this minimum distance approach should be equally good.
On Mon, 23 Jan 2023, 00:08 Adrian Mariano, avm4@cornell.edu wrote:
nophead, he didn't mean two cones meeting at a point. He meant two
(skewed) cones intersecting at an edge, with one cone apex on the top
circle and one cone apex on the bottom circle.
My method is global. It is not going for a single nearest point, but
minimizing the distance of all the points jointly. So the fact that there
is an obvious way to get a single point in bad correspondence doesn't show
that the full solution will actually come out that way. If you use the
arc-length approach you have to pick a starting point, and there you could
run into trouble if you don't use a global approach of some sort to do it.
Here's the case you describe, where the bottom of the ellipse is closer to
the back of the circle, and the solution is by distance minimization. That
doesn't lead it to map to the back of the circle.
[image: image.png]
On Sun, Jan 22, 2023 at 1:27 PM nop head nop.head@gmail.com wrote:
If you map the points of a circle at one end to points on the other end
180 degrees further round that gives a 1:1 mapping that will make two cones
meeting at a point in between.
If you go for the nearest point with the top circle sharply inclined it
the lower points could be nearer the back of the base than the correct
point which is more distant at the back of the top.
On Sun, 22 Jan 2023 at 17:24, Adrian Mariano avm4@cornell.edu wrote:
Sanjeev, I don't understand why using minimum length should be any less
robust than minimum area. I think the difference in results of the two
methods, at least in the context of my implementation, would be very
small. And it would be especially small in the case like the one you
show, where the triangles are long and thin, because in that case, length
(distance) is a good approximation for area.
[image: image.png]
On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
also i think if the 2 sections are not in parallel plane, minimum
length system may not work.
e.g. this is produced with area minimizing option
[image: Screenshot 2023-01-22 at 9.37.51 PM.png]
On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan kennethrsloan@gmail.com
wrote:
If you don’t get 2 cones with circles displaced by a diameter, then
you are not minimizing area.
O(n^2) is the best you can do for global optimization. Faster
schemes don’t guarantee optimality.
Arc length is O(n), but can lead to strange local results when one
curve is very detailed in only one area. For “nornal” cases, it’s fine -
which is why it’s my first choice for most practical applications.
On Sun, Jan 22, 2023 at 09:35 Adrian Mariano avm4@cornell.edu wrote:
Can you elaborate a bit on when or how minimizing area is expected to
be better than minimizing distance? What about the specific case of
adding an edge to a non-coplanar quadrilateral? Is there an argument in
favor of minimum area vs choosing the shortest edge to add?
The Fuchs, et al., paper sounds like it's trying to make the
algorithm more efficient by being clever. Unfortunately, being clever
rarely works in OpenSCAD code, because the overhead of the clever thing
ends up being O(N^2). It might work for Sanjeev, since he's using Python
instead of OpenSCAD. I'd have to spend more time studying it than seems
warranted, since I have a working, debugged code that is fast enough for
the cases on which I think it's relevant, namely the ones with few points.
Cases with lots of points (smooth curves) are too slow with my code, but
the results aren't notable. These cases seem better served by the arc
length approach---or the arc length approach seems to produce the same
result as the distance minimizer approach without all the computation
time.
I remain baffled about the idea that displacement causes problems. I
used 2 circles and every displacement produces a reasonable result. No
clue what you mean about 2 cones sharing an edge. Are you saying all the
points from one circle map to a single point on the other circle? That's
impossible in my code because it isn't an onto mapping from the source
shape to the target shape. (Note: source shape is the one with more
vertices, or either one in case of identical vertex count.) In fact, the
only way the mapping can "fail" when you have the same number of points on
each shape is by introducing a twist, which will have a larger distance, so
it won't be the optimal solution. The only candidate mappings are twists
of each other in this situation. It sounds like you're maybe talking
about a very simple method that locally picks the closest point on the
other shape, not a global optimization that minimizes the distance summed
over all pairs of matched points, with the constraint that every point is
in a pair.
[image: image.png]
On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <
kennethrsloan@gmail.com> wrote:
Excellent! Follow the references for many details on other methods
and optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are
either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
version - but please read the original (and the maybe the Sloan & Painter
papers, if you can find them.
Beware of the issue with laterally displaced slices. Scaling can
also be a problem. Rotation is very difficult to get right. We handled it
by creating intermediate phantom slices, but didn’t get it quite right.
Note that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The
simplest test is to use two “circles” and a range of displacements.
Perfect alignment yields a perfect cylinder. Displacement causes a crease
to appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
I think this minimum distance approach should be equally good.
On Mon, 23 Jan 2023, 00:08 Adrian Mariano, <avm4@cornell.edu> wrote:
> nophead, he didn't mean two cones meeting at a point. He meant two
> (skewed) cones intersecting at an edge, with one cone apex on the top
> circle and one cone apex on the bottom circle.
>
> My method is *global*. It is not going for a single nearest point, but
> minimizing the distance of all the points jointly. So the fact that there
> is an obvious way to get a single point in bad correspondence doesn't show
> that the full solution will actually come out that way. If you use the
> arc-length approach you have to pick a starting point, and there you could
> run into trouble if you don't use a global approach of some sort to do it.
>
> Here's the case you describe, where the bottom of the ellipse is closer to
> the back of the circle, and the solution is by distance minimization. That
> doesn't lead it to map to the back of the circle.
>
> [image: image.png]
>
>
> On Sun, Jan 22, 2023 at 1:27 PM nop head <nop.head@gmail.com> wrote:
>
>> If you map the points of a circle at one end to points on the other end
>> 180 degrees further round that gives a 1:1 mapping that will make two cones
>> meeting at a point in between.
>>
>> If you go for the nearest point with the top circle sharply inclined it
>> the lower points could be nearer the back of the base than the correct
>> point which is more distant at the back of the top.
>>
>> On Sun, 22 Jan 2023 at 17:24, Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Sanjeev, I don't understand why using minimum length should be any less
>>> robust than minimum area. I think the difference in results of the two
>>> methods, at least in the context of my implementation, would be very
>>> small. And it would be *especially* small in the case like the one you
>>> show, where the triangles are long and thin, because in that case, length
>>> (distance) is a good approximation for area.
>>>
>>> [image: image.png]
>>>
>>>
>>> On Sun, Jan 22, 2023 at 11:10 AM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> also i think if the 2 sections are not in parallel plane, minimum
>>>> length system may not work.
>>>>
>>>> e.g. this is produced with area minimizing option
>>>> [image: Screenshot 2023-01-22 at 9.37.51 PM.png]
>>>>
>>>>
>>>> On Sun, 22 Jan 2023 at 21:31, Kenneth R Sloan <kennethrsloan@gmail.com>
>>>> wrote:
>>>>
>>>>> If you don’t get 2 cones with circles displaced by a diameter, then
>>>>> you are not minimizing area.
>>>>>
>>>>> O(n^2) is the best you can do for global optimization. Faster
>>>>> schemes don’t guarantee optimality.
>>>>>
>>>>> Arc length is O(n), but can lead to strange local results when one
>>>>> curve is very detailed in only one area. For “nornal” cases, it’s fine -
>>>>> which is why it’s my first choice for most practical applications.
>>>>>
>>>>> On Sun, Jan 22, 2023 at 09:35 Adrian Mariano <avm4@cornell.edu> wrote:
>>>>>
>>>>>> Can you elaborate a bit on when or how minimizing area is expected to
>>>>>> be better than minimizing distance? What about the specific case of
>>>>>> adding an edge to a non-coplanar quadrilateral? Is there an argument in
>>>>>> favor of minimum area vs choosing the shortest edge to add?
>>>>>>
>>>>>> The Fuchs, et al., paper sounds like it's trying to make the
>>>>>> algorithm more efficient by being clever. Unfortunately, being clever
>>>>>> rarely works in OpenSCAD code, because the overhead of the clever thing
>>>>>> ends up being O(N^2). It might work for Sanjeev, since he's using Python
>>>>>> instead of OpenSCAD. I'd have to spend more time studying it than seems
>>>>>> warranted, since I have a working, debugged code that is fast enough for
>>>>>> the cases on which I think it's relevant, namely the ones with few points.
>>>>>> Cases with lots of points (smooth curves) are too slow with my code, but
>>>>>> the results aren't notable. These cases seem better served by the arc
>>>>>> length approach---or the arc length approach seems to produce the same
>>>>>> result as the distance minimizer approach without all the computation
>>>>>> time.
>>>>>>
>>>>>> I remain baffled about the idea that displacement causes problems. I
>>>>>> used 2 circles and every displacement produces a reasonable result. No
>>>>>> clue what you mean about 2 cones sharing an edge. Are you saying all the
>>>>>> points from one circle map to a single point on the other circle? That's
>>>>>> impossible in my code because it isn't an onto mapping from the source
>>>>>> shape to the target shape. (Note: source shape is the one with more
>>>>>> vertices, or either one in case of identical vertex count.) In fact, the
>>>>>> only way the mapping can "fail" when you have the same number of points on
>>>>>> each shape is by introducing a twist, which will have a larger distance, so
>>>>>> it won't be the optimal solution. The only candidate mappings are twists
>>>>>> of each other in this situation. It sounds like you're maybe talking
>>>>>> about a very simple method that locally picks the closest point on the
>>>>>> other shape, not a global optimization that minimizes the distance summed
>>>>>> over all pairs of matched points, with the constraint that every point is
>>>>>> in a pair.
>>>>>>
>>>>>> [image: image.png]
>>>>>>
>>>>>>
>>>>>> On Sun, Jan 22, 2023 at 9:15 AM Kenneth R Sloan <
>>>>>> kennethrsloan@gmail.com> wrote:
>>>>>>
>>>>>>> Excellent! Follow the references for many details on other methods
>>>>>>> and optimization techniques.
>>>>>>>
>>>>>>> The Fuchs, Kedem, and Uselton paper is essential. The others are
>>>>>>> either tweaks on that, or alternate approaches. My Fig.2 is the shorthand
>>>>>>> version - but please read the original (and the maybe the Sloan & Painter
>>>>>>> papers, if you can find them.
>>>>>>>
>>>>>>> Beware of the issue with laterally displaced slices. Scaling can
>>>>>>> also be a problem. Rotation is very difficult to get right. We handled it
>>>>>>> by creating intermediate phantom slices, but didn’t get it quite right.
>>>>>>> Note that we ignored rotation in the “Surfaces From Contours” paper.
>>>>>>>
>>>>>>> You may want to experiment with the displacement issue. The
>>>>>>> simplest test is to use two “circles” and a range of displacements.
>>>>>>> Perfect alignment yields a perfect cylinder. Displacement causes a crease
>>>>>>> to appear. The limiting case is two cones sharing a single edge.
>>>>>>>
>>>>>>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <
>>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>>
>>>>>>>> I tried this minimum area approach and this works.
>>>>>>>> the optimised model is really quite good.
>>>>>>>>
>>>>>>>>
>>>>>>> --
>>>>>>> -Kenneth Sloan
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> --
>>>>> -Kenneth Sloan
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

RW
Rogier Wolff
Mon, Jan 23, 2023 10:48 AM
On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
I think this minimum distance approach should be equally good.
I think "funnies" can occur when the source shape is not continuous
(i.e. the mathematical term)...
You might be tempted to make:
difference () {
cylinder (d1 = 10, d2=0, h=10);
cylinder (d1 = 5, d2=0, h=5);
}
with an extrusion of a ring changing ito a circle
module myobject (h)
{
difference () {
circle (10-h);
if (h < 5) circle (5-h);
}
}
But that's going to give a lot of problems around [0,0,5]. Even with
"nearest".
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110 **
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.
On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
> I think this minimum distance approach should be equally good.
I think "funnies" can occur when the source shape is not continuous
(i.e. the mathematical term)...
You might be tempted to make:
difference () {
cylinder (d1 = 10, d2=0, h=10);
cylinder (d1 = 5, d2=0, h=5);
}
with an extrusion of a ring changing ito a circle
module myobject (h)
{
difference () {
circle (10-h);
if (h < 5) circle (5-h);
}
}
But that's going to give a lot of problems around [0,0,5]. Even with
"nearest".
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110 **
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.