AM
Adrian Mariano
Mon, Jan 23, 2023 11:12 AM
Rogier, in your example the number of contours changes. This is what
Kenneth's paper calls the "branching" problem and algorithms like mine (and
I assume Sanjeev's) don't even address this problem at all. We are
looking just at the problem of how to align one contour with another one.
On Mon, Jan 23, 2023 at 5:50 AM Rogier Wolff R.E.Wolff@bitwizard.nl wrote:
On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
I think this minimum distance approach should be equally good.
I think "funnies" can occur when the source shape is not continuous
(i.e. the mathematical term)...
You might be tempted to make:
difference () {
cylinder (d1 = 10, d2=0, h=10);
cylinder (d1 = 5, d2=0, h=5);
}
with an extrusion of a ring changing ito a circle
module myobject (h)
{
difference () {
circle (10-h);
if (h < 5) circle (5-h);
}
}
But that's going to give a lot of problems around [0,0,5]. Even with
"nearest".
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110
**
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Rogier, in your example the number of contours changes. This is what
Kenneth's paper calls the "branching" problem and algorithms like mine (and
I assume Sanjeev's) don't even address this problem at all. We are
looking just at the problem of how to align one contour with another one.
On Mon, Jan 23, 2023 at 5:50 AM Rogier Wolff <R.E.Wolff@bitwizard.nl> wrote:
> On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
> > I think this minimum distance approach should be equally good.
>
>
> I think "funnies" can occur when the source shape is not continuous
> (i.e. the mathematical term)...
>
> You might be tempted to make:
>
> difference () {
> cylinder (d1 = 10, d2=0, h=10);
> cylinder (d1 = 5, d2=0, h=5);
> }
>
> with an extrusion of a ring changing ito a circle
> module myobject (h)
> {
> difference () {
> circle (10-h);
> if (h < 5) circle (5-h);
> }
> }
>
> But that's going to give a lot of problems around [0,0,5]. Even with
> "nearest".
>
> Roger.
>
> --
> ** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110
> **
> ** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
> f equals m times a. When your f is steady, and your m is going down
> your a is going up. -- Chris Hadfield about flying up the space shuttle.
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Mon, Jan 23, 2023 11:33 AM
yes, in my case i can only use this when the number of points in both the
sections are same.
although a generic arrangement can be developed by following
[sec1]*len(sec2) and [sec2]*len(sec1) to make them equal and this works,
but i dont think this is correct
regards
On Mon, 23 Jan 2023 at 16:43, Adrian Mariano avm4@cornell.edu wrote:
Rogier, in your example the number of contours changes. This is what
Kenneth's paper calls the "branching" problem and algorithms like mine (and
I assume Sanjeev's) don't even address this problem at all. We are
looking just at the problem of how to align one contour with another one.
On Mon, Jan 23, 2023 at 5:50 AM Rogier Wolff R.E.Wolff@bitwizard.nl
wrote:
On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
I think this minimum distance approach should be equally good.
I think "funnies" can occur when the source shape is not continuous
(i.e. the mathematical term)...
You might be tempted to make:
difference () {
cylinder (d1 = 10, d2=0, h=10);
cylinder (d1 = 5, d2=0, h=5);
}
with an extrusion of a ring changing ito a circle
module myobject (h)
{
difference () {
circle (10-h);
if (h < 5) circle (5-h);
}
}
But that's going to give a lot of problems around [0,0,5]. Even with
"nearest".
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110
**
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233
**
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
yes, in my case i can only use this when the number of points in both the
sections are same.
although a generic arrangement can be developed by following
[sec1]*len(sec2) and [sec2]*len(sec1) to make them equal and this works,
but i dont think this is correct
regards
On Mon, 23 Jan 2023 at 16:43, Adrian Mariano <avm4@cornell.edu> wrote:
> Rogier, in your example the number of contours changes. This is what
> Kenneth's paper calls the "branching" problem and algorithms like mine (and
> I assume Sanjeev's) don't even address this problem at all. We are
> looking just at the problem of how to align one contour with another one.
>
> On Mon, Jan 23, 2023 at 5:50 AM Rogier Wolff <R.E.Wolff@bitwizard.nl>
> wrote:
>
>> On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
>> > I think this minimum distance approach should be equally good.
>>
>>
>> I think "funnies" can occur when the source shape is not continuous
>> (i.e. the mathematical term)...
>>
>> You might be tempted to make:
>>
>> difference () {
>> cylinder (d1 = 10, d2=0, h=10);
>> cylinder (d1 = 5, d2=0, h=5);
>> }
>>
>> with an extrusion of a ring changing ito a circle
>> module myobject (h)
>> {
>> difference () {
>> circle (10-h);
>> if (h < 5) circle (5-h);
>> }
>> }
>>
>> But that's going to give a lot of problems around [0,0,5]. Even with
>> "nearest".
>>
>> Roger.
>>
>> --
>> ** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110
>> **
>> ** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233
>> **
>> f equals m times a. When your f is steady, and your m is going down
>> your a is going up. -- Chris Hadfield about flying up the space shuttle.
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

GS
Guenther Sohler
Mon, Jan 23, 2023 1:35 PM
Hi,
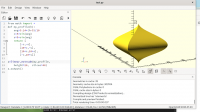
Right now i am developing linear_extrude with an ARBRITARY profile (with
help of python)
possible application might look like this:
[image: image.png]
hoping that this can become baseline sometime in the future.
working locally already here :)
On Sun, Jan 22, 2023 at 3:15 PM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be
a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest test
is to use two “circles” and a range of displacements. Perfect alignment
yields a perfect cylinder. Displacement causes a crease to appear. The
limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
Hi,
Right now i am developing linear_extrude with an ARBRITARY profile (with
help of python)
possible application might look like this:
[image: image.png]
hoping that this can become baseline sometime in the future.
working locally already here :)
On Sun, Jan 22, 2023 at 3:15 PM Kenneth R Sloan <kennethrsloan@gmail.com>
wrote:
> Excellent! Follow the references for many details on other methods and
> optimization techniques.
>
> The Fuchs, Kedem, and Uselton paper is essential. The others are either
> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
> - but please read the original (and the maybe the Sloan & Painter papers,
> if you can find them.
>
> Beware of the issue with laterally displaced slices. Scaling can also be
> a problem. Rotation is very difficult to get right. We handled it by
> creating intermediate phantom slices, but didn’t get it quite right. Note
> that we ignored rotation in the “Surfaces From Contours” paper.
>
> You may want to experiment with the displacement issue. The simplest test
> is to use two “circles” and a range of displacements. Perfect alignment
> yields a perfect cylinder. Displacement causes a crease to appear. The
> limiting case is two cones sharing a single edge.
>
> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> I tried this minimum area approach and this works.
>> the optimised model is really quite good.
>>
>>
> --
> -Kenneth Sloan
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Mon, Jan 23, 2023 2:54 PM
If I have to import my python library openscsd1.py and use, how will that
work.
Also would not like to overwrite the native openscad modules.
On Mon, 23 Jan, 2023, 7:07 pm Guenther Sohler, guenther.sohler@gmail.com
wrote:
Hi,
Right now i am developing linear_extrude with an ARBRITARY profile (with
help of python)
possible application might look like this:
[image: image.png]
hoping that this can become baseline sometime in the future.
working locally already here :)
On Sun, Jan 22, 2023 at 3:15 PM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be
a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
If I have to import my python library openscsd1.py and use, how will that
work.
Also would not like to overwrite the native openscad modules.
On Mon, 23 Jan, 2023, 7:07 pm Guenther Sohler, <guenther.sohler@gmail.com>
wrote:
> Hi,
>
> Right now i am developing linear_extrude with an ARBRITARY profile (with
> help of python)
>
> possible application might look like this:
>
> [image: image.png]
> hoping that this can become baseline sometime in the future.
> working locally already here :)
>
>
>
> On Sun, Jan 22, 2023 at 3:15 PM Kenneth R Sloan <kennethrsloan@gmail.com>
> wrote:
>
>> Excellent! Follow the references for many details on other methods and
>> optimization techniques.
>>
>> The Fuchs, Kedem, and Uselton paper is essential. The others are either
>> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
>> - but please read the original (and the maybe the Sloan & Painter papers,
>> if you can find them.
>>
>> Beware of the issue with laterally displaced slices. Scaling can also be
>> a problem. Rotation is very difficult to get right. We handled it by
>> creating intermediate phantom slices, but didn’t get it quite right. Note
>> that we ignored rotation in the “Surfaces From Contours” paper.
>>
>> You may want to experiment with the displacement issue. The simplest
>> test is to use two “circles” and a range of displacements. Perfect
>> alignment yields a perfect cylinder. Displacement causes a crease to
>> appear. The limiting case is two cones sharing a single edge.
>>
>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <sprabhakar2006@gmail.com>
>> wrote:
>>
>>> I tried this minimum area approach and this works.
>>> the optimised model is really quite good.
>>>
>>>
>> --
>> -Kenneth Sloan
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Mon, Jan 23, 2023 9:15 PM
It sounds like you are writing a function that duplicates the skin()
function found originally in list-comprehension-demos and expanded in
BOSL2, though if you truly mean arbitrary shapes it will be interesting.
So you can connect 4 rings to a single hexagon, say?
For your example, it can be done without python:
include<BOSL2-fork/std.scad>
function prof(h) =
let(
ang = 180*(h-5)/10,
c=5sin(ang),
s=5sin(ang)
)
[[-c,-s,h],[10+c,-s,h],[10+c,10+s,h],[-c,10+s,h]];
profiles = [for(i=[0:1/2:20]) prof(i)];
skin(profiles,slices=0);
On Mon, Jan 23, 2023 at 8:37 AM Guenther Sohler guenther.sohler@gmail.com
wrote:
Hi,
Right now i am developing linear_extrude with an ARBRITARY profile (with
help of python)
possible application might look like this:
[image: image.png]
hoping that this can become baseline sometime in the future.
working locally already here :)
On Sun, Jan 22, 2023 at 3:15 PM Kenneth R Sloan kennethrsloan@gmail.com
wrote:
Excellent! Follow the references for many details on other methods and
optimization techniques.
The Fuchs, Kedem, and Uselton paper is essential. The others are either
tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
- but please read the original (and the maybe the Sloan & Painter papers,
if you can find them.
Beware of the issue with laterally displaced slices. Scaling can also be
a problem. Rotation is very difficult to get right. We handled it by
creating intermediate phantom slices, but didn’t get it quite right. Note
that we ignored rotation in the “Surfaces From Contours” paper.
You may want to experiment with the displacement issue. The simplest
test is to use two “circles” and a range of displacements. Perfect
alignment yields a perfect cylinder. Displacement causes a crease to
appear. The limiting case is two cones sharing a single edge.
On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I tried this minimum area approach and this works.
the optimised model is really quite good.
It sounds like you are writing a function that duplicates the skin()
function found originally in list-comprehension-demos and expanded in
BOSL2, though if you truly mean *arbitrary* shapes it will be interesting.
So you can connect 4 rings to a single hexagon, say?
For your example, it can be done without python:
include<BOSL2-fork/std.scad>
function prof(h) =
let(
ang = 180*(h-5)/10,
c=5*sin(ang),
s=5*sin(ang)
)
[[-c,-s,h],[10+c,-s,h],[10+c,10+s,h],[-c,10+s,h]];
profiles = [for(i=[0:1/2:20]) prof(i)];
skin(profiles,slices=0);
On Mon, Jan 23, 2023 at 8:37 AM Guenther Sohler <guenther.sohler@gmail.com>
wrote:
> Hi,
>
> Right now i am developing linear_extrude with an ARBRITARY profile (with
> help of python)
>
> possible application might look like this:
>
> [image: image.png]
> hoping that this can become baseline sometime in the future.
> working locally already here :)
>
>
>
> On Sun, Jan 22, 2023 at 3:15 PM Kenneth R Sloan <kennethrsloan@gmail.com>
> wrote:
>
>> Excellent! Follow the references for many details on other methods and
>> optimization techniques.
>>
>> The Fuchs, Kedem, and Uselton paper is essential. The others are either
>> tweaks on that, or alternate approaches. My Fig.2 is the shorthand version
>> - but please read the original (and the maybe the Sloan & Painter papers,
>> if you can find them.
>>
>> Beware of the issue with laterally displaced slices. Scaling can also be
>> a problem. Rotation is very difficult to get right. We handled it by
>> creating intermediate phantom slices, but didn’t get it quite right. Note
>> that we ignored rotation in the “Surfaces From Contours” paper.
>>
>> You may want to experiment with the displacement issue. The simplest
>> test is to use two “circles” and a range of displacements. Perfect
>> alignment yields a perfect cylinder. Displacement causes a crease to
>> appear. The limiting case is two cones sharing a single edge.
>>
>> On Sun, Jan 22, 2023 at 07:04 Sanjeev Prabhakar <sprabhakar2006@gmail.com>
>> wrote:
>>
>>> I tried this minimum area approach and this works.
>>> the optimised model is really quite good.
>>>
>>>
>> --
>> -Kenneth Sloan
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Mon, Jan 23, 2023 9:18 PM
Sanjeev, I make no assumption that the number of points in both sections
are the same. It didn't look like you were making this assumption: in
your example with the star the number of points is different.
But I assume that there is only one contour at each layer, so you cannot
have a ring, because that has two contours. You would have to handle that
by modeling the hole separately from the outside of the object.
On Mon, Jan 23, 2023 at 6:34 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
yes, in my case i can only use this when the number of points in both the
sections are same.
although a generic arrangement can be developed by following
[sec1]*len(sec2) and [sec2]*len(sec1) to make them equal and this works,
but i dont think this is correct
regards
On Mon, 23 Jan 2023 at 16:43, Adrian Mariano avm4@cornell.edu wrote:
Rogier, in your example the number of contours changes. This is what
Kenneth's paper calls the "branching" problem and algorithms like mine (and
I assume Sanjeev's) don't even address this problem at all. We are
looking just at the problem of how to align one contour with another one.
On Mon, Jan 23, 2023 at 5:50 AM Rogier Wolff R.E.Wolff@bitwizard.nl
wrote:
On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
I think this minimum distance approach should be equally good.
I think "funnies" can occur when the source shape is not continuous
(i.e. the mathematical term)...
You might be tempted to make:
difference () {
cylinder (d1 = 10, d2=0, h=10);
cylinder (d1 = 5, d2=0, h=5);
}
with an extrusion of a ring changing ito a circle
module myobject (h)
{
difference () {
circle (10-h);
if (h < 5) circle (5-h);
}
}
But that's going to give a lot of problems around [0,0,5]. Even with
"nearest".
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ **
+31-15-2049110 **
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233
**
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Sanjeev, I make no assumption that the number of points in both sections
are the same. It didn't look like you were making this assumption: in
your example with the star the number of points is different.
But I assume that there is only one contour at each layer, so you cannot
have a ring, because that has two contours. You would have to handle that
by modeling the hole separately from the outside of the object.
On Mon, Jan 23, 2023 at 6:34 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> yes, in my case i can only use this when the number of points in both the
> sections are same.
>
> although a generic arrangement can be developed by following
> [sec1]*len(sec2) and [sec2]*len(sec1) to make them equal and this works,
> but i dont think this is correct
>
> regards
>
> On Mon, 23 Jan 2023 at 16:43, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Rogier, in your example the number of contours changes. This is what
>> Kenneth's paper calls the "branching" problem and algorithms like mine (and
>> I assume Sanjeev's) don't even address this problem at all. We are
>> looking just at the problem of how to align one contour with another one.
>>
>> On Mon, Jan 23, 2023 at 5:50 AM Rogier Wolff <R.E.Wolff@bitwizard.nl>
>> wrote:
>>
>>> On Mon, Jan 23, 2023 at 07:23:11AM +0530, Sanjeev Prabhakar wrote:
>>> > I think this minimum distance approach should be equally good.
>>>
>>>
>>> I think "funnies" can occur when the source shape is not continuous
>>> (i.e. the mathematical term)...
>>>
>>> You might be tempted to make:
>>>
>>> difference () {
>>> cylinder (d1 = 10, d2=0, h=10);
>>> cylinder (d1 = 5, d2=0, h=5);
>>> }
>>>
>>> with an extrusion of a ring changing ito a circle
>>> module myobject (h)
>>> {
>>> difference () {
>>> circle (10-h);
>>> if (h < 5) circle (5-h);
>>> }
>>> }
>>>
>>> But that's going to give a lot of problems around [0,0,5]. Even with
>>> "nearest".
>>>
>>> Roger.
>>>
>>> --
>>> ** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ **
>>> +31-15-2049110 **
>>> ** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233
>>> **
>>> f equals m times a. When your f is steady, and your m is going down
>>> your a is going up. -- Chris Hadfield about flying up the space shuttle.
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Mon, Jan 23, 2023 10:46 PM
For producing a polyhedron, the number of points in different levels needs
to be same is what I assume. If there is any other way, I am not sure.
In the example shared, points were made same with ray intersection method.
From the center of the sections, lines were drawn in circular orientation
to find intersections.
Since these are 360 lines, the points in each section were 360. But in this
case vertex to vertex mapping is not possible.
The other method I use is nearest point mapping method depending on the
shape of the 2 sections and most of the time this works if the sections are
convex.
Now with the new minimum distance orientation solution, this new method of
[sec1]×len(sec2) and [sec2]×len(sec1) can be used. This cannot be directly
used though, all the similar points needs to be grouped together to work.
On Tue, 24 Jan, 2023, 2:49 am Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I make no assumption that the number of points in both sections
are the same. It didn't look like you were making this assumption: in
your example with the star the number of points is different.
But I assume that there is only one contour at each layer, so you cannot
have a ring, because that has two contours. You would have to handle that
by modeling the hole separately from the outside of the object.
For producing a polyhedron, the number of points in different levels needs
to be same is what I assume. If there is any other way, I am not sure.
In the example shared, points were made same with ray intersection method.
From the center of the sections, lines were drawn in circular orientation
to find intersections.
Since these are 360 lines, the points in each section were 360. But in this
case vertex to vertex mapping is not possible.
The other method I use is nearest point mapping method depending on the
shape of the 2 sections and most of the time this works if the sections are
convex.
Now with the new minimum distance orientation solution, this new method of
[sec1]×len(sec2) and [sec2]×len(sec1) can be used. This cannot be directly
used though, all the similar points needs to be grouped together to work.
On Tue, 24 Jan, 2023, 2:49 am Adrian Mariano, <avm4@cornell.edu> wrote:
> Sanjeev, I make no assumption that the number of points in both sections
> are the same. It didn't look like you were making this assumption: in
> your example with the star the number of points is different.
>
> But I assume that there is only one contour at each layer, so you cannot
> have a ring, because that has two contours. You would have to handle that
> by modeling the hole separately from the outside of the object.
>
>
>

AM
Adrian Mariano
Mon, Jan 23, 2023 11:16 PM
My approach is to duplicate points, so if you want to match a pentagon to a
hexagon, you duplicate one of the pentagon's points so that you have a
pentagon with 6 points. Then the points can be aligned. Then you resample
the edges of the points, and linearly interpolate to generate the desired
number of slices. This generates a polyhedron with some degenerate faces,
which can then be discarded automatically.
So when I'm doing a distance optimization, that optimization is done on the
5 points of the pentagon and 6 points of the hexagon, not on the resampled
curves. This ensures that the corners align with each other, which (I
think) produces the best outcome.
I don't think I understand what you mean about [sec1]×len(sec2) and
[sec2]×len(sec1). If I don't want to use the minimum distance method, but
instead want to use the arc length based approach, then I resample (or
originally generate) the curves so that they have the same number of
points, uniformly spaced in length along the curve. Then it's a question
of deciding where to start. I do this by considering every possible
starting position (rotations of the point lists of one of the curves) and
computing the total distance between all pairs. Choosing the one with
minimum total distance gives a good starting position.
My other approach, which I think resembles your rays approach is as
follows: given one curve and a point to map, find a tangent plane at that
point on the curve such that the tangent plane also intersects the other
curve in a single point. That defines the mapping. I never understood how
your rays method works when the curves are in 3 space, not parallel to each
other.
On Mon, Jan 23, 2023 at 5:50 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
For producing a polyhedron, the number of points in different levels needs
to be same is what I assume. If there is any other way, I am not sure.
In the example shared, points were made same with ray intersection method.
From the center of the sections, lines were drawn in circular orientation
to find intersections.
Since these are 360 lines, the points in each section were 360. But in
this case vertex to vertex mapping is not possible.
The other method I use is nearest point mapping method depending on the
shape of the 2 sections and most of the time this works if the sections are
convex.
Now with the new minimum distance orientation solution, this new method of
[sec1]×len(sec2) and [sec2]×len(sec1) can be used. This cannot be directly
used though, all the similar points needs to be grouped together to work.
On Tue, 24 Jan, 2023, 2:49 am Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I make no assumption that the number of points in both sections
are the same. It didn't look like you were making this assumption: in
your example with the star the number of points is different.
But I assume that there is only one contour at each layer, so you cannot
have a ring, because that has two contours. You would have to handle that
by modeling the hole separately from the outside of the object.
My approach is to duplicate points, so if you want to match a pentagon to a
hexagon, you duplicate one of the pentagon's points so that you have a
pentagon with 6 points. Then the points can be aligned. Then you resample
the edges of the points, and linearly interpolate to generate the desired
number of slices. This generates a polyhedron with some degenerate faces,
which can then be discarded automatically.
So when I'm doing a distance optimization, that optimization is done on the
5 points of the pentagon and 6 points of the hexagon, not on the resampled
curves. This ensures that the corners align with each other, which (I
think) produces the best outcome.
I don't think I understand what you mean about [sec1]×len(sec2) and
[sec2]×len(sec1). If I don't want to use the minimum distance method, but
instead want to use the arc length based approach, then I resample (or
originally generate) the curves so that they have the same number of
points, uniformly spaced in length along the curve. Then it's a question
of deciding where to start. I do this by considering every possible
starting position (rotations of the point lists of one of the curves) and
computing the total distance between all pairs. Choosing the one with
minimum total distance gives a good starting position.
My other approach, which I think resembles your rays approach is as
follows: given one curve and a point to map, find a tangent plane at that
point on the curve such that the tangent plane also intersects the other
curve in a single point. That defines the mapping. I never understood how
your rays method works when the curves are in 3 space, not parallel to each
other.
On Mon, Jan 23, 2023 at 5:50 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> For producing a polyhedron, the number of points in different levels needs
> to be same is what I assume. If there is any other way, I am not sure.
>
> In the example shared, points were made same with ray intersection method.
>
> From the center of the sections, lines were drawn in circular orientation
> to find intersections.
> Since these are 360 lines, the points in each section were 360. But in
> this case vertex to vertex mapping is not possible.
>
> The other method I use is nearest point mapping method depending on the
> shape of the 2 sections and most of the time this works if the sections are
> convex.
>
> Now with the new minimum distance orientation solution, this new method of
> [sec1]×len(sec2) and [sec2]×len(sec1) can be used. This cannot be directly
> used though, all the similar points needs to be grouped together to work.
>
>
> On Tue, 24 Jan, 2023, 2:49 am Adrian Mariano, <avm4@cornell.edu> wrote:
>
>> Sanjeev, I make no assumption that the number of points in both sections
>> are the same. It didn't look like you were making this assumption: in
>> your example with the star the number of points is different.
>>
>> But I assume that there is only one contour at each layer, so you cannot
>> have a ring, because that has two contours. You would have to handle that
>> by modeling the hole separately from the outside of the object.
>>
>>
>> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
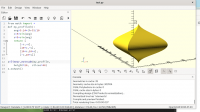
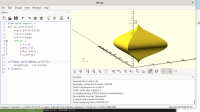
Mon, Jan 23, 2023 11:59 PM
following is the code in python which matches a pentagon with an octagon
with minimum distance method without any slices:
sec1=circle(5,s=6)
sec2=circle(7,s=9)
sec3=c2t3(concatenate(array([sec1]*len(sec2)).transpose(1,0,2)))
sec4=translate([0,0,10],concatenate(array([sec2]*len(sec1)).transpose(1,0,2)))
sol=align_sec(sec3,sec4)
with open('/Users/sanjeevprabhakar/iCloud Drive
(Archive)/Documents/Download/openscad/trial.scad','w+') as f:
f.write(f'''
{swp(sol)}
''')
function c2t3 converts a 2d to 3d by adding 0 in place of 'z' axis.
function translate is used to translate a 2d section up by 10 units in this
case and hence making it 3d
function align_sec is for aligning the points
you can notice the grouping of points with python numpy functions
following result is produced:
[image: Screenshot 2023-01-24 at 5.28.03 AM.png]
Align function is written yesterday and is not checked for any possible
bugs yet, but it works as of now in various similar cases
On Tue, 24 Jan 2023 at 04:48, Adrian Mariano avm4@cornell.edu wrote:
My approach is to duplicate points, so if you want to match a pentagon to
a hexagon, you duplicate one of the pentagon's points so that you have a
pentagon with 6 points. Then the points can be aligned. Then you resample
the edges of the points, and linearly interpolate to generate the desired
number of slices. This generates a polyhedron with some degenerate faces,
which can then be discarded automatically.
So when I'm doing a distance optimization, that optimization is done on
the 5 points of the pentagon and 6 points of the hexagon, not on the
resampled curves. This ensures that the corners align with each other,
which (I think) produces the best outcome.
I don't think I understand what you mean about [sec1]×len(sec2) and
[sec2]×len(sec1). If I don't want to use the minimum distance method, but
instead want to use the arc length based approach, then I resample (or
originally generate) the curves so that they have the same number of
points, uniformly spaced in length along the curve. Then it's a question
of deciding where to start. I do this by considering every possible
starting position (rotations of the point lists of one of the curves) and
computing the total distance between all pairs. Choosing the one with
minimum total distance gives a good starting position.
My other approach, which I think resembles your rays approach is as
follows: given one curve and a point to map, find a tangent plane at that
point on the curve such that the tangent plane also intersects the other
curve in a single point. That defines the mapping. I never understood how
your rays method works when the curves are in 3 space, not parallel to each
other.
following is the code in python which matches a pentagon with an octagon
with minimum distance method without any slices:
sec1=circle(5,s=6)
sec2=circle(7,s=9)
sec3=c2t3(concatenate(array([sec1]*len(sec2)).transpose(1,0,2)))
sec4=translate([0,0,10],concatenate(array([sec2]*len(sec1)).transpose(1,0,2)))
sol=align_sec(sec3,sec4)
with open('/Users/sanjeevprabhakar/iCloud Drive
(Archive)/Documents/Download/openscad/trial.scad','w+') as f:
f.write(f'''
{swp(sol)}
''')
function c2t3 converts a 2d to 3d by adding 0 in place of 'z' axis.
function translate is used to translate a 2d section up by 10 units in this
case and hence making it 3d
function align_sec is for aligning the points
you can notice the grouping of points with python numpy functions
following result is produced:
[image: Screenshot 2023-01-24 at 5.28.03 AM.png]
Align function is written yesterday and is not checked for any possible
bugs yet, but it works as of now in various similar cases
On Tue, 24 Jan 2023 at 04:48, Adrian Mariano <avm4@cornell.edu> wrote:
> My approach is to duplicate points, so if you want to match a pentagon to
> a hexagon, you duplicate one of the pentagon's points so that you have a
> pentagon with 6 points. Then the points can be aligned. Then you resample
> the edges of the points, and linearly interpolate to generate the desired
> number of slices. This generates a polyhedron with some degenerate faces,
> which can then be discarded automatically.
>
> So when I'm doing a distance optimization, that optimization is done on
> the 5 points of the pentagon and 6 points of the hexagon, not on the
> resampled curves. This ensures that the corners align with each other,
> which (I think) produces the best outcome.
>
> I don't think I understand what you mean about [sec1]×len(sec2) and
> [sec2]×len(sec1). If I don't want to use the minimum distance method, but
> instead want to use the arc length based approach, then I resample (or
> originally generate) the curves so that they have the same number of
> points, uniformly spaced in length along the curve. Then it's a question
> of deciding where to start. I do this by considering every possible
> starting position (rotations of the point lists of one of the curves) and
> computing the total distance between all pairs. Choosing the one with
> minimum total distance gives a good starting position.
>
> My other approach, which I think resembles your rays approach is as
> follows: given one curve and a point to map, find a tangent plane at that
> point on the curve such that the tangent plane also intersects the other
> curve in a single point. That defines the mapping. I never understood how
> your rays method works when the curves are in 3 space, not parallel to each
> other.
>
>
>
>
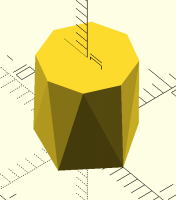

AM
Adrian Mariano
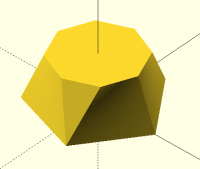
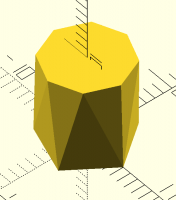
Tue, Jan 24, 2023 12:13 AM
This is my result for pentagon to octagon. It has two obviously curved
faces. (All faces are somewhat curved.)
[image: image.png]
On Mon, Jan 23, 2023 at 7:00 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
following is the code in python which matches a pentagon with an octagon
with minimum distance method without any slices:
sec1=circle(5,s=6)
sec2=circle(7,s=9)
sec3=c2t3(concatenate(array([sec1]*len(sec2)).transpose(1,0,2)))
sec4=translate([0,0,10],concatenate(array([sec2]*len(sec1)).transpose(1,0,2)))
sol=align_sec(sec3,sec4)
with open('/Users/sanjeevprabhakar/iCloud Drive
(Archive)/Documents/Download/openscad/trial.scad','w+') as f:
f.write(f'''
{swp(sol)}
''')
function c2t3 converts a 2d to 3d by adding 0 in place of 'z' axis.
function translate is used to translate a 2d section up by 10 units in
this case and hence making it 3d
function align_sec is for aligning the points
you can notice the grouping of points with python numpy functions
following result is produced:
[image: Screenshot 2023-01-24 at 5.28.03 AM.png]
Align function is written yesterday and is not checked for any possible
bugs yet, but it works as of now in various similar cases
On Tue, 24 Jan 2023 at 04:48, Adrian Mariano avm4@cornell.edu wrote:
My approach is to duplicate points, so if you want to match a pentagon to
a hexagon, you duplicate one of the pentagon's points so that you have a
pentagon with 6 points. Then the points can be aligned. Then you resample
the edges of the points, and linearly interpolate to generate the desired
number of slices. This generates a polyhedron with some degenerate faces,
which can then be discarded automatically.
So when I'm doing a distance optimization, that optimization is done on
the 5 points of the pentagon and 6 points of the hexagon, not on the
resampled curves. This ensures that the corners align with each other,
which (I think) produces the best outcome.
I don't think I understand what you mean about [sec1]×len(sec2) and
[sec2]×len(sec1). If I don't want to use the minimum distance method, but
instead want to use the arc length based approach, then I resample (or
originally generate) the curves so that they have the same number of
points, uniformly spaced in length along the curve. Then it's a question
of deciding where to start. I do this by considering every possible
starting position (rotations of the point lists of one of the curves) and
computing the total distance between all pairs. Choosing the one with
minimum total distance gives a good starting position.
My other approach, which I think resembles your rays approach is as
follows: given one curve and a point to map, find a tangent plane at that
point on the curve such that the tangent plane also intersects the other
curve in a single point. That defines the mapping. I never understood how
your rays method works when the curves are in 3 space, not parallel to each
other.
This is my result for pentagon to octagon. It has two obviously curved
faces. (All faces are somewhat curved.)
[image: image.png]
On Mon, Jan 23, 2023 at 7:00 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> following is the code in python which matches a pentagon with an octagon
> with minimum distance method without any slices:
>
> sec1=circle(5,s=6)
> sec2=circle(7,s=9)
>
> sec3=c2t3(concatenate(array([sec1]*len(sec2)).transpose(1,0,2)))
>
> sec4=translate([0,0,10],concatenate(array([sec2]*len(sec1)).transpose(1,0,2)))
>
> sol=align_sec(sec3,sec4)
>
> with open('/Users/sanjeevprabhakar/iCloud Drive
> (Archive)/Documents/Download/openscad/trial.scad','w+') as f:
> f.write(f'''
> {swp(sol)}
> ''')
>
> function c2t3 converts a 2d to 3d by adding 0 in place of 'z' axis.
> function translate is used to translate a 2d section up by 10 units in
> this case and hence making it 3d
> function align_sec is for aligning the points
> you can notice the grouping of points with python numpy functions
>
> following result is produced:
> [image: Screenshot 2023-01-24 at 5.28.03 AM.png]
>
> Align function is written yesterday and is not checked for any possible
> bugs yet, but it works as of now in various similar cases
>
> On Tue, 24 Jan 2023 at 04:48, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> My approach is to duplicate points, so if you want to match a pentagon to
>> a hexagon, you duplicate one of the pentagon's points so that you have a
>> pentagon with 6 points. Then the points can be aligned. Then you resample
>> the edges of the points, and linearly interpolate to generate the desired
>> number of slices. This generates a polyhedron with some degenerate faces,
>> which can then be discarded automatically.
>>
>> So when I'm doing a distance optimization, that optimization is done on
>> the 5 points of the pentagon and 6 points of the hexagon, not on the
>> resampled curves. This ensures that the corners align with each other,
>> which (I think) produces the best outcome.
>>
>> I don't think I understand what you mean about [sec1]×len(sec2) and
>> [sec2]×len(sec1). If I don't want to use the minimum distance method, but
>> instead want to use the arc length based approach, then I resample (or
>> originally generate) the curves so that they have the same number of
>> points, uniformly spaced in length along the curve. Then it's a question
>> of deciding where to start. I do this by considering every possible
>> starting position (rotations of the point lists of one of the curves) and
>> computing the total distance between all pairs. Choosing the one with
>> minimum total distance gives a good starting position.
>>
>> My other approach, which I think resembles your rays approach is as
>> follows: given one curve and a point to map, find a tangent plane at that
>> point on the curve such that the tangent plane also intersects the other
>> curve in a single point. That defines the mapping. I never understood how
>> your rays method works when the curves are in 3 space, not parallel to each
>> other.
>>
>>
>>
>> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>