SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 3:14 AM
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
here is a small video on how to use this:
https://youtu.be/5XvgnYlwkgM
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
here is a small video on how to use this:
https://youtu.be/5XvgnYlwkgM

WF
William F. Adams
Sun, Aug 11, 2024 4:03 AM
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
Flat out amazing!
Is there a mechanism for interpolating between multiple such curves so as to create a surface?
William
On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via Discuss <discuss@lists.openscad.org> wrote:
>I have written a function to compute bspline curves purely in openscad.
>This could be useful many here
Flat out _amazing_!
Is there a mechanism for interpolating between multiple such curves so as to create a surface?
William

SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 4:51 AM
Thanks William
Do you mean bspline surfaces?
I have not yet written any function for that, even in python, may be
sometime in future, but I guess should not be too difficult.
On Sun, 11 Aug, 2024, 9:33 am William F. Adams, willadams@aol.com wrote:
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
Flat out amazing!
Is there a mechanism for interpolating between multiple such curves so as
to create a surface?
William
Thanks William
Do you mean bspline surfaces?
I have not yet written any function for that, even in python, may be
sometime in future, but I guess should not be too difficult.
On Sun, 11 Aug, 2024, 9:33 am William F. Adams, <willadams@aol.com> wrote:
> On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via
> Discuss <discuss@lists.openscad.org> wrote:
>
> >I have written a function to compute bspline curves purely in openscad.
> >This could be useful many here
>
> Flat out _amazing_!
>
> Is there a mechanism for interpolating between multiple such curves so as
> to create a surface?
>
> William
>
>

RD
Revar Desmera
Sun, Aug 11, 2024 8:31 AM
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
Flat out amazing!
Is there a mechanism for interpolating between multiple such curves so as to create a surface?
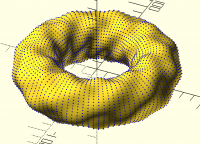
A couple years ago I wrote some B-Spline code that we were considering for inclusion into BOSL2. It had some code fiddling around with making B-spline surface patches:
include <BOSL2/std.scad>
function bspline(path, closed=false, splinesteps=8) =
assert(is_path(path) && len(path)>3)
assert(is_finite(splinesteps))
assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)), "splinesteps must be an integer power of 2.")
let(
lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
path = closed? path :
concat([path[0]], path, [last(path)])
)
_bspline_recurse(path, closed=closed, lev=lev);
function _bspline_recurse(path, closed=false, lev) =
lev == 0 ? path :
let(
endknots = [
[1.0, 0.0, 0.0, 0.0],
[0.5, 0.5, 0.0, 0.0],
[0.0, 0.75, 0.25, 0.0],
[0.0, 0.1875, 0.6875, 0.125],
],
midknots = [
[0.5, 0.5, 0.0 ],
[0.125, 0.75, 0.125],
],
plen = len(path)
)
closed
? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] * select(path,i,i+2)], closed, lev=lev-1)
: _bspline_recurse(
[
for(i=[0:1:min(3,plen-3)]) endknots[i] * select(path,0,3),
for(i=[3:1:plen-4], j=[0,1]) midknots[j] * select(path,i-1,i+1),
midknots[0] * select(path,-4,-2),
for(i=[min(3,plen-2):-1:0]) endknots[i] * select(path,[-1:-1:-4]),
],
closed,
lev=lev-1
);
function bspline_patch(patch, splinesteps=8, col_wrap=false, row_wrap=false) =
let(
bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch) row[i]], closed=col_wrap, splinesteps=splinesteps)],
bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1) row[i]], closed=row_wrap, splinesteps=splinesteps)]
)
vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
rsteps = 96;
csteps = 48;
hreps = 10;
vreps = 4;
ssteps = 2;
r_maj = 50;
r_min = 20;
patch = [
for (i = [0:1:rsteps-1]) [
for (j = [0:1:csteps-1])
let(
u = i/rsteps,
v = j/csteps,
r_var = sin(v360vreps) * sin(u360hreps) * 2,
m = zrot(u360) * right(r_maj) * yrot(-v360)
)
apply(m, [r_min+r_var, 0, 0])
]
];
color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true, row_wrap=true);
vnf_polyhedron(vnf);
Blue dots are patch control points:

> On Aug 10, 2024, at 9:03 PM, William F. Adams via Discuss <discuss@lists.openscad.org> wrote:
>
> On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via Discuss <discuss@lists.openscad.org> wrote:
>
>> I have written a function to compute bspline curves purely in openscad.
>> This could be useful many here
>
> Flat out _amazing_!
>
> Is there a mechanism for interpolating between multiple such curves so as to create a surface?
>
A couple years ago I wrote some B-Spline code that we were considering for inclusion into BOSL2. It had some code fiddling around with making B-spline surface patches:
include <BOSL2/std.scad>
function bspline(path, closed=false, splinesteps=8) =
assert(is_path(path) && len(path)>3)
assert(is_finite(splinesteps))
assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)), "splinesteps must be an integer power of 2.")
let(
lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
path = closed? path :
concat([path[0]], path, [last(path)])
)
_bspline_recurse(path, closed=closed, lev=lev);
function _bspline_recurse(path, closed=false, lev) =
lev == 0 ? path :
let(
endknots = [
[1.0, 0.0, 0.0, 0.0],
[0.5, 0.5, 0.0, 0.0],
[0.0, 0.75, 0.25, 0.0],
[0.0, 0.1875, 0.6875, 0.125],
],
midknots = [
[0.5, 0.5, 0.0 ],
[0.125, 0.75, 0.125],
],
plen = len(path)
)
closed
? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] * select(path,i,i+2)], closed, lev=lev-1)
: _bspline_recurse(
[
for(i=[0:1:min(3,plen-3)]) endknots[i] * select(path,0,3),
for(i=[3:1:plen-4], j=[0,1]) midknots[j] * select(path,i-1,i+1),
midknots[0] * select(path,-4,-2),
for(i=[min(3,plen-2):-1:0]) endknots[i] * select(path,[-1:-1:-4]),
],
closed,
lev=lev-1
);
function bspline_patch(patch, splinesteps=8, col_wrap=false, row_wrap=false) =
let(
bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch) row[i]], closed=col_wrap, splinesteps=splinesteps)],
bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1) row[i]], closed=row_wrap, splinesteps=splinesteps)]
)
vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
rsteps = 96;
csteps = 48;
hreps = 10;
vreps = 4;
ssteps = 2;
r_maj = 50;
r_min = 20;
patch = [
for (i = [0:1:rsteps-1]) [
for (j = [0:1:csteps-1])
let(
u = i/rsteps,
v = j/csteps,
r_var = sin(v*360*vreps) * sin(u*360*hreps) * 2,
m = zrot(u*360) * right(r_maj) * yrot(-v*360)
)
apply(m, [r_min+r_var, 0, 0])
]
];
color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true, row_wrap=true);
vnf_polyhedron(vnf);
Blue dots are patch control points:

- Revar

RD
Revar Desmera
Sun, Aug 11, 2024 8:38 AM
A more detailed view of the surface:

I have written a function to compute bspline curves purely in openscad.
This could be useful many here
Flat out amazing!
Is there a mechanism for interpolating between multiple such curves so as to create a surface?
A couple years ago I wrote some B-Spline code that we were considering for inclusion into BOSL2. It had some code fiddling around with making B-spline surface patches:
include <BOSL2/std.scad>
function bspline(path, closed=false, splinesteps=8) =
assert(is_path(path) && len(path)>3)
assert(is_finite(splinesteps))
assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)), "splinesteps must be an integer power of 2.")
let(
lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
path = closed? path :
concat([path[0]], path, [last(path)])
)
_bspline_recurse(path, closed=closed, lev=lev);
function _bspline_recurse(path, closed=false, lev) =
lev == 0 ? path :
let(
endknots = [
[1.0, 0.0, 0.0, 0.0],
[0.5, 0.5, 0.0, 0.0],
[0.0, 0.75, 0.25, 0.0],
[0.0, 0.1875, 0.6875, 0.125],
],
midknots = [
[0.5, 0.5, 0.0 ],
[0.125, 0.75, 0.125],
],
plen = len(path)
)
closed
? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] * select(path,i,i+2)], closed, lev=lev-1)
: _bspline_recurse(
[
for(i=[0:1:min(3,plen-3)]) endknots[i] * select(path,0,3),
for(i=[3:1:plen-4], j=[0,1]) midknots[j] * select(path,i-1,i+1),
midknots[0] * select(path,-4,-2),
for(i=[min(3,plen-2):-1:0]) endknots[i] * select(path,[-1:-1:-4]),
],
closed,
lev=lev-1
);
function bspline_patch(patch, splinesteps=8, col_wrap=false, row_wrap=false) =
let(
bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch) row[i]], closed=col_wrap, splinesteps=splinesteps)],
bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1) row[i]], closed=row_wrap, splinesteps=splinesteps)]
)
vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
rsteps = 96;
csteps = 48;
hreps = 10;
vreps = 4;
ssteps = 2;
r_maj = 50;
r_min = 20;
patch = [
for (i = [0:1:rsteps-1]) [
for (j = [0:1:csteps-1])
let(
u = i/rsteps,
v = j/csteps,
r_var = sin(v360vreps) * sin(u360hreps) * 2,
m = zrot(u360) * right(r_maj) * yrot(-v360)
)
apply(m, [r_min+r_var, 0, 0])
]
];
color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true, row_wrap=true);
vnf_polyhedron(vnf);
Blue dots are patch control points:
<Screenshot 2024-08-11 at 1.29.21 AM.png>
A more detailed view of the surface:

- Revar
> On Aug 11, 2024, at 1:31 AM, Revar Desmera <revarbat@gmail.com> wrote:
>
>
>
>> On Aug 10, 2024, at 9:03 PM, William F. Adams via Discuss <discuss@lists.openscad.org> wrote:
>>
>> On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via Discuss <discuss@lists.openscad.org> wrote:
>>
>>> I have written a function to compute bspline curves purely in openscad.
>>> This could be useful many here
>>
>> Flat out _amazing_!
>>
>> Is there a mechanism for interpolating between multiple such curves so as to create a surface?
>>
>
> A couple years ago I wrote some B-Spline code that we were considering for inclusion into BOSL2. It had some code fiddling around with making B-spline surface patches:
>
> include <BOSL2/std.scad>
>
> function bspline(path, closed=false, splinesteps=8) =
> assert(is_path(path) && len(path)>3)
> assert(is_finite(splinesteps))
> assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)), "splinesteps must be an integer power of 2.")
> let(
> lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
> path = closed? path :
> concat([path[0]], path, [last(path)])
> )
> _bspline_recurse(path, closed=closed, lev=lev);
>
> function _bspline_recurse(path, closed=false, lev) =
> lev == 0 ? path :
> let(
> endknots = [
> [1.0, 0.0, 0.0, 0.0],
> [0.5, 0.5, 0.0, 0.0],
> [0.0, 0.75, 0.25, 0.0],
> [0.0, 0.1875, 0.6875, 0.125],
> ],
> midknots = [
> [0.5, 0.5, 0.0 ],
> [0.125, 0.75, 0.125],
> ],
> plen = len(path)
> )
> closed
> ? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] * select(path,i,i+2)], closed, lev=lev-1)
> : _bspline_recurse(
> [
> for(i=[0:1:min(3,plen-3)]) endknots[i] * select(path,0,3),
> for(i=[3:1:plen-4], j=[0,1]) midknots[j] * select(path,i-1,i+1),
> midknots[0] * select(path,-4,-2),
> for(i=[min(3,plen-2):-1:0]) endknots[i] * select(path,[-1:-1:-4]),
> ],
> closed,
> lev=lev-1
> );
>
> function bspline_patch(patch, splinesteps=8, col_wrap=false, row_wrap=false) =
> let(
> bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch) row[i]], closed=col_wrap, splinesteps=splinesteps)],
> bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1) row[i]], closed=row_wrap, splinesteps=splinesteps)]
> )
> vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
>
> rsteps = 96;
> csteps = 48;
> hreps = 10;
> vreps = 4;
> ssteps = 2;
> r_maj = 50;
> r_min = 20;
>
> patch = [
> for (i = [0:1:rsteps-1]) [
> for (j = [0:1:csteps-1])
> let(
> u = i/rsteps,
> v = j/csteps,
> r_var = sin(v*360*vreps) * sin(u*360*hreps) * 2,
> m = zrot(u*360) * right(r_maj) * yrot(-v*360)
> )
> apply(m, [r_min+r_var, 0, 0])
> ]
> ];
>
> color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
> vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true, row_wrap=true);
> vnf_polyhedron(vnf);
>
> Blue dots are patch control points:
> <Screenshot 2024-08-11 at 1.29.21 AM.png>
>
> - Revar


SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 1:01 PM
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or maybe use
for creating surfaces separately.
creating a closed section from a list will surely be very useful. I need to
check the application in various cases.
Few days back I created a model of car seat, there it should be much easier
if bspline is used instead of bezier
On Sun, 11 Aug, 2024, 2:09 pm Revar Desmera via Discuss, <
discuss@lists.openscad.org> wrote:
A more detailed view of the surface:
[image: Screenshot 2024-08-11 at 1.37.33 AM.png]
On Aug 11, 2024, at 1:31 AM, Revar Desmera revarbat@gmail.com wrote:
On Aug 10, 2024, at 9:03 PM, William F. Adams via Discuss <
discuss@lists.openscad.org> wrote:
On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via
Discuss discuss@lists.openscad.org wrote:
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
Flat out amazing!
Is there a mechanism for interpolating between multiple such curves so as
to create a surface?
A couple years ago I wrote some B-Spline code that we were considering for
inclusion into BOSL2. It had some code fiddling around with making
B-spline surface patches:
include <BOSL2/std.scad>
function bspline(path, closed=false, splinesteps=8) =
assert(is_path(path) && len(path)>3)
assert(is_finite(splinesteps))
assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)),
"splinesteps must be an integer power of 2.")
let(
lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
path = closed? path :
concat([path[0]], path, [last(path)])
)
_bspline_recurse(path, closed=closed, lev=lev);
function _bspline_recurse(path, closed=false, lev) =
lev == 0 ? path :
let(
endknots = [
[1.0, 0.0, 0.0, 0.0],
[0.5, 0.5, 0.0, 0.0],
[0.0, 0.75, 0.25, 0.0],
[0.0, 0.1875, 0.6875, 0.125],
],
midknots = [
[0.5, 0.5, 0.0 ],
[0.125, 0.75, 0.125],
],
plen = len(path)
)
closed
? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] *
select(path,i,i+2)], closed, lev=lev-1)
: _bspline_recurse(
[
for(i=[0:1:min(3,plen-3)]) endknots[i] *
select(path,0,3),
for(i=[3:1:plen-4], j=[0,1]) midknots[j] *
select(path,i-1,i+1),
midknots[0] * select(path,-4,-2),
for(i=[min(3,plen-2):-1:0]) endknots[i] *
select(path,[-1:-1:-4]),
],
closed,
lev=lev-1
);
function bspline_patch(patch, splinesteps=8, col_wrap=false,
row_wrap=false) =
let(
bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch)
row[i]], closed=col_wrap, splinesteps=splinesteps)],
bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1)
row[i]], closed=row_wrap, splinesteps=splinesteps)]
)
vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
rsteps = 96;
csteps = 48;
hreps = 10;
vreps = 4;
ssteps = 2;
r_maj = 50;
r_min = 20;
patch = [
for (i = [0:1:rsteps-1]) [
for (j = [0:1:csteps-1])
let(
u = i/rsteps,
v = j/csteps,
r_var = sin(v360vreps) * sin(u360hreps) * 2,
m = zrot(u360) * right(r_maj) * yrot(-v360)
)
apply(m, [r_min+r_var, 0, 0])
]
];
color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true,
row_wrap=true);
vnf_polyhedron(vnf);
Blue dots are patch control points:
<Screenshot 2024-08-11 at 1.29.21 AM.png>
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or maybe use
for creating surfaces separately.
creating a closed section from a list will surely be very useful. I need to
check the application in various cases.
Few days back I created a model of car seat, there it should be much easier
if bspline is used instead of bezier
On Sun, 11 Aug, 2024, 2:09 pm Revar Desmera via Discuss, <
discuss@lists.openscad.org> wrote:
> A more detailed view of the surface:
> [image: Screenshot 2024-08-11 at 1.37.33 AM.png]
>
> - Revar
>
>
> On Aug 11, 2024, at 1:31 AM, Revar Desmera <revarbat@gmail.com> wrote:
>
>
>
> On Aug 10, 2024, at 9:03 PM, William F. Adams via Discuss <
> discuss@lists.openscad.org> wrote:
>
> On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via
> Discuss <discuss@lists.openscad.org> wrote:
>
> I have written a function to compute bspline curves purely in openscad.
> This could be useful many here
>
>
> Flat out _amazing_!
>
> Is there a mechanism for interpolating between multiple such curves so as
> to create a surface?
>
>
> A couple years ago I wrote some B-Spline code that we were considering for
> inclusion into BOSL2. It had some code fiddling around with making
> B-spline surface patches:
>
> include <BOSL2/std.scad>
>
> function bspline(path, closed=false, splinesteps=8) =
> assert(is_path(path) && len(path)>3)
> assert(is_finite(splinesteps))
> assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)),
> "splinesteps must be an integer power of 2.")
> let(
> lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
> path = closed? path :
> concat([path[0]], path, [last(path)])
> )
> _bspline_recurse(path, closed=closed, lev=lev);
>
> function _bspline_recurse(path, closed=false, lev) =
> lev == 0 ? path :
> let(
> endknots = [
> [1.0, 0.0, 0.0, 0.0],
> [0.5, 0.5, 0.0, 0.0],
> [0.0, 0.75, 0.25, 0.0],
> [0.0, 0.1875, 0.6875, 0.125],
> ],
> midknots = [
> [0.5, 0.5, 0.0 ],
> [0.125, 0.75, 0.125],
> ],
> plen = len(path)
> )
> closed
> ? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] *
> select(path,i,i+2)], closed, lev=lev-1)
> : _bspline_recurse(
> [
> for(i=[0:1:min(3,plen-3)]) endknots[i] *
> select(path,0,3),
> for(i=[3:1:plen-4], j=[0,1]) midknots[j] *
> select(path,i-1,i+1),
> midknots[0] * select(path,-4,-2),
> for(i=[min(3,plen-2):-1:0]) endknots[i] *
> select(path,[-1:-1:-4]),
> ],
> closed,
> lev=lev-1
> );
>
> function bspline_patch(patch, splinesteps=8, col_wrap=false,
> row_wrap=false) =
> let(
> bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch)
> row[i]], closed=col_wrap, splinesteps=splinesteps)],
> bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1)
> row[i]], closed=row_wrap, splinesteps=splinesteps)]
> )
> vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
>
> rsteps = 96;
> csteps = 48;
> hreps = 10;
> vreps = 4;
> ssteps = 2;
> r_maj = 50;
> r_min = 20;
>
> patch = [
> for (i = [0:1:rsteps-1]) [
> for (j = [0:1:csteps-1])
> let(
> u = i/rsteps,
> v = j/csteps,
> r_var = sin(v*360*vreps) * sin(u*360*hreps) * 2,
> m = zrot(u*360) * right(r_maj) * yrot(-v*360)
> )
> apply(m, [r_min+r_var, 0, 0])
> ]
> ];
>
> color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
> vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true,
> row_wrap=true);
> vnf_polyhedron(vnf);
>
> Blue dots are patch control points:
> <Screenshot 2024-08-11 at 1.29.21 AM.png>
>
> - Revar
>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>



AM
Adrian Mariano
Sun, Aug 11, 2024 1:10 PM
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or maybe
use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I need
to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
On Sun, 11 Aug, 2024, 2:09 pm Revar Desmera via Discuss, <
discuss@lists.openscad.org> wrote:
A more detailed view of the surface:
[image: Screenshot 2024-08-11 at 1.37.33 AM.png]
On Aug 11, 2024, at 1:31 AM, Revar Desmera revarbat@gmail.com wrote:
On Aug 10, 2024, at 9:03 PM, William F. Adams via Discuss <
discuss@lists.openscad.org> wrote:
On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via
Discuss discuss@lists.openscad.org wrote:
I have written a function to compute bspline curves purely in openscad.
This could be useful many here
Flat out amazing!
Is there a mechanism for interpolating between multiple such curves so as
to create a surface?
A couple years ago I wrote some B-Spline code that we were considering
for inclusion into BOSL2. It had some code fiddling around with making
B-spline surface patches:
include <BOSL2/std.scad>
function bspline(path, closed=false, splinesteps=8) =
assert(is_path(path) && len(path)>3)
assert(is_finite(splinesteps))
assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)),
"splinesteps must be an integer power of 2.")
let(
lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
path = closed? path :
concat([path[0]], path, [last(path)])
)
_bspline_recurse(path, closed=closed, lev=lev);
function _bspline_recurse(path, closed=false, lev) =
lev == 0 ? path :
let(
endknots = [
[1.0, 0.0, 0.0, 0.0],
[0.5, 0.5, 0.0, 0.0],
[0.0, 0.75, 0.25, 0.0],
[0.0, 0.1875, 0.6875, 0.125],
],
midknots = [
[0.5, 0.5, 0.0 ],
[0.125, 0.75, 0.125],
],
plen = len(path)
)
closed
? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] *
select(path,i,i+2)], closed, lev=lev-1)
: _bspline_recurse(
[
for(i=[0:1:min(3,plen-3)]) endknots[i] *
select(path,0,3),
for(i=[3:1:plen-4], j=[0,1]) midknots[j] *
select(path,i-1,i+1),
midknots[0] * select(path,-4,-2),
for(i=[min(3,plen-2):-1:0]) endknots[i] *
select(path,[-1:-1:-4]),
],
closed,
lev=lev-1
);
function bspline_patch(patch, splinesteps=8, col_wrap=false,
row_wrap=false) =
let(
bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch)
row[i]], closed=col_wrap, splinesteps=splinesteps)],
bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1)
row[i]], closed=row_wrap, splinesteps=splinesteps)]
)
vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
rsteps = 96;
csteps = 48;
hreps = 10;
vreps = 4;
ssteps = 2;
r_maj = 50;
r_min = 20;
patch = [
for (i = [0:1:rsteps-1]) [
for (j = [0:1:csteps-1])
let(
u = i/rsteps,
v = j/csteps,
r_var = sin(v360vreps) * sin(u360hreps) * 2,
m = zrot(u360) * right(r_maj) * yrot(-v360)
)
apply(m, [r_min+r_var, 0, 0])
]
];
color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true,
row_wrap=true);
vnf_polyhedron(vnf);
Blue dots are patch control points:
<Screenshot 2024-08-11 at 1.29.21 AM.png>
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
> To create surfaces there are better ways than bspline I suppose.
> It is mainly useful for creating smoother paths for extruding or maybe
> use for creating surfaces separately.
>
> creating a closed section from a list will surely be very useful. I need
> to check the application in various cases.
>
> Few days back I created a model of car seat, there it should be much
> easier if bspline is used instead of bezier
>
> On Sun, 11 Aug, 2024, 2:09 pm Revar Desmera via Discuss, <
> discuss@lists.openscad.org> wrote:
>
>> A more detailed view of the surface:
>> [image: Screenshot 2024-08-11 at 1.37.33 AM.png]
>>
>> - Revar
>>
>>
>> On Aug 11, 2024, at 1:31 AM, Revar Desmera <revarbat@gmail.com> wrote:
>>
>>
>>
>> On Aug 10, 2024, at 9:03 PM, William F. Adams via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>> On Saturday, August 10, 2024 at 11:14:40 PM EDT, Sanjeev Prabhakar via
>> Discuss <discuss@lists.openscad.org> wrote:
>>
>> I have written a function to compute bspline curves purely in openscad.
>> This could be useful many here
>>
>>
>> Flat out _amazing_!
>>
>> Is there a mechanism for interpolating between multiple such curves so as
>> to create a surface?
>>
>>
>> A couple years ago I wrote some B-Spline code that we were considering
>> for inclusion into BOSL2. It had some code fiddling around with making
>> B-spline surface patches:
>>
>> include <BOSL2/std.scad>
>>
>> function bspline(path, closed=false, splinesteps=8) =
>> assert(is_path(path) && len(path)>3)
>> assert(is_finite(splinesteps))
>> assert(floor(ln(splinesteps)/ln(2)) == (ln(splinesteps)/ln(2)),
>> "splinesteps must be an integer power of 2.")
>> let(
>> lev = max(0, ceil(ln(splinesteps) / ln(2)) ),
>> path = closed? path :
>> concat([path[0]], path, [last(path)])
>> )
>> _bspline_recurse(path, closed=closed, lev=lev);
>>
>> function _bspline_recurse(path, closed=false, lev) =
>> lev == 0 ? path :
>> let(
>> endknots = [
>> [1.0, 0.0, 0.0, 0.0],
>> [0.5, 0.5, 0.0, 0.0],
>> [0.0, 0.75, 0.25, 0.0],
>> [0.0, 0.1875, 0.6875, 0.125],
>> ],
>> midknots = [
>> [0.5, 0.5, 0.0 ],
>> [0.125, 0.75, 0.125],
>> ],
>> plen = len(path)
>> )
>> closed
>> ? _bspline_recurse([for(i=idx(path), j=[0,1]) midknots[j] *
>> select(path,i,i+2)], closed, lev=lev-1)
>> : _bspline_recurse(
>> [
>> for(i=[0:1:min(3,plen-3)]) endknots[i] *
>> select(path,0,3),
>> for(i=[3:1:plen-4], j=[0,1]) midknots[j] *
>> select(path,i-1,i+1),
>> midknots[0] * select(path,-4,-2),
>> for(i=[min(3,plen-2):-1:0]) endknots[i] *
>> select(path,[-1:-1:-4]),
>> ],
>> closed,
>> lev=lev-1
>> );
>>
>> function bspline_patch(patch, splinesteps=8, col_wrap=false,
>> row_wrap=false) =
>> let(
>> bswall1 = [for (i = idx(patch[0])) bspline([for (row=patch)
>> row[i]], closed=col_wrap, splinesteps=splinesteps)],
>> bswall2 = [for (i = idx(bswall1[0])) bspline([for (row=bswall1)
>> row[i]], closed=row_wrap, splinesteps=splinesteps)]
>> )
>> vnf_vertex_array(bswall2, col_wrap=col_wrap, row_wrap=row_wrap);
>>
>> rsteps = 96;
>> csteps = 48;
>> hreps = 10;
>> vreps = 4;
>> ssteps = 2;
>> r_maj = 50;
>> r_min = 20;
>>
>> patch = [
>> for (i = [0:1:rsteps-1]) [
>> for (j = [0:1:csteps-1])
>> let(
>> u = i/rsteps,
>> v = j/csteps,
>> r_var = sin(v*360*vreps) * sin(u*360*hreps) * 2,
>> m = zrot(u*360) * right(r_maj) * yrot(-v*360)
>> )
>> apply(m, [r_min+r_var, 0, 0])
>> ]
>> ];
>>
>> color("blue") move_copies(flatten(patch)) sphere(0.5,$fn=8);
>> vnf = bspline_patch(patch, splinesteps=ssteps, col_wrap=true,
>> row_wrap=true);
>> vnf_polyhedron(vnf);
>>
>> Blue dots are patch control points:
>> <Screenshot 2024-08-11 at 1.29.21 AM.png>
>>
>> - Revar
>>
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 1:35 PM
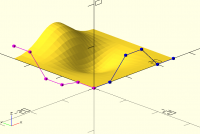
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control
points each) with 2 methods
- converted both lines to bspline curves and created a surface by adding
the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or maybe
use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I need
to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control
points each) with 2 methods
1. converted both lines to bspline curves and created a surface by adding
the points (time: 0.015s)
2. by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
> What better ways than bspline exist for creating surfaces? I had the
> impression that NURBS were the tool for this out in the big world, and they
> are just a slight generalization of bspline. I'm planning and
> implementation of bspline/NURBS at some point, but efficient implementation
> in OpenSCAD may be difficult, compared to beziers, which can be done very
> fast as a matrix multiply.
>
> On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> To create surfaces there are better ways than bspline I suppose.
>> It is mainly useful for creating smoother paths for extruding or maybe
>> use for creating surfaces separately.
>>
>> creating a closed section from a list will surely be very useful. I need
>> to check the application in various cases.
>>
>> Few days back I created a model of car seat, there it should be much
>> easier if bspline is used instead of bezier
>>
>

WF
William F. Adams
Sun, Aug 11, 2024 1:51 PM
I am not qualified to evaluate which mathematical representation is better or even what advantages or disadvantages each has. (will gladly accept reading lists which might help me understand such discussions)
It is my hope that I can wrap my mind around this code and use it to generalize a mechanism where a series of 2D spline is both output as a series of short lines (where multiple iterations of a tool are hull()ed together so as to show the effect of a cutting tool and at the same time represent the same spline as a series of arcs and lines in a matching DXF.
Folks who are curious as to this context may see:
https://github.com/WillAdams/gcodepreview/blob/main/gcodepreview.pdf
which I believe is approaching a usable state for cutting lines and arcs (though now that I write that I wonder if I should do inside and outside DXF arcs for a given arc toolpath).
Anyway if anyone wants to discuss this aspect, please create a new e-mail thread, and please preface it with a reading list which once I read and understand the texts will make it possible for me to follow along.
William
--
Sphinx of black quartz, judge my vow.
https://designinto3d.com/
I am not qualified to evaluate which mathematical representation is better or even what advantages or disadvantages each has. (will gladly accept reading lists which might help me understand such discussions)
It is my hope that I can wrap my mind around this code and use it to generalize a mechanism where a series of 2D spline is both output as a series of short lines (where multiple iterations of a tool are hull()ed together so as to show the effect of a cutting tool and at the same time represent the same spline as a series of arcs and lines in a matching DXF.
Folks who are curious as to this context may see:
https://github.com/WillAdams/gcodepreview/blob/main/gcodepreview.pdf
which I believe is approaching a usable state for cutting lines and arcs (though now that I write that I wonder if I should do inside and outside DXF arcs for a given arc toolpath).
Anyway if anyone wants to discuss this aspect, please create a new e-mail thread, and please preface it with a reading list which once I read and understand the texts will make it possible for me to follow along.
William
--
Sphinx of black quartz, judge my vow.
https://designinto3d.com/

AM
Adrian Mariano
Sun, Aug 11, 2024 2:35 PM
I am not sure I understand what method 1 is. A surface could easily
require 100 points along each edge, which means 10k points in total. I
know that for bezier surfaces run time was a concern. It got slow with
surfaces that had a lot of points, and since the bezier calculations cannot
be cached you take that run-time hit every time you do anything with your
model, so run time performance was important. Implementing beziers using
matrix multiplication was a 10x-20x speed improvement compared to
recursively using the de casteljau algorithm. The problem with b-splines
is that the knots create a bunch of variability in the structure of the
shape. I guess your implementation assumes uniformly spaced knots?
On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control
points each) with 2 methods
- converted both lines to bspline curves and created a surface by adding
the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or maybe
use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I need
to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
I am not sure I understand what method 1 is. A surface could easily
require 100 points along each edge, which means 10k points in total. I
know that for bezier surfaces run time *was* a concern. It got slow with
surfaces that had a lot of points, and since the bezier calculations cannot
be cached you take that run-time hit every time you do anything with your
model, so run time performance was important. Implementing beziers using
matrix multiplication was a 10x-20x speed improvement compared to
recursively using the de casteljau algorithm. The problem with b-splines
is that the knots create a bunch of variability in the structure of the
shape. I guess your implementation assumes uniformly spaced knots?
On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I did a small test of efficiency
>
> following surface is created using 2 lines (blue and magenta, 6 control
> points each) with 2 methods
> 1. converted both lines to bspline curves and created a surface by adding
> the points (time: 0.015s)
> 2. by directly using the formula for bspline surface (time: 0.53s)
>
> method 1 is around 35 times faster.
>
> Maybe the algorithm written is not efficient, but this is a very small
> surface with only 400 points overall
>
> [image: Screenshot 2024-08-11 at 6.55.26 PM.png]
>
> On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> What better ways than bspline exist for creating surfaces? I had the
>> impression that NURBS were the tool for this out in the big world, and they
>> are just a slight generalization of bspline. I'm planning and
>> implementation of bspline/NURBS at some point, but efficient implementation
>> in OpenSCAD may be difficult, compared to beziers, which can be done very
>> fast as a matrix multiply.
>>
>> On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>>> To create surfaces there are better ways than bspline I suppose.
>>> It is mainly useful for creating smoother paths for extruding or maybe
>>> use for creating surfaces separately.
>>>
>>> creating a closed section from a list will surely be very useful. I need
>>> to check the application in various cases.
>>>
>>> Few days back I created a model of car seat, there it should be much
>>> easier if bspline is used instead of bezier
>>>
>>