AM
Adrian Mariano
Sun, Aug 11, 2024 2:39 PM
I am not qualified to evaluate which mathematical representation is better
or even what advantages or disadvantages each has. (will gladly accept
reading lists which might help me understand such discussions)
It is my hope that I can wrap my mind around this code and use it to
generalize a mechanism where a series of 2D spline is both output as a
series of short lines (where multiple iterations of a tool are hull()ed
together so as to show the effect of a cutting tool and at the same time
represent the same spline as a series of arcs and lines in a matching DXF.
Folks who are curious as to this context may see:
https://github.com/WillAdams/gcodepreview/blob/main/gcodepreview.pdf
which I believe is approaching a usable state for cutting lines and arcs
(though now that I write that I wonder if I should do inside and outside
DXF arcs for a given arc toolpath).
Anyway if anyone wants to discuss this aspect, please create a new e-mail
thread, and please preface it with a reading list which once I read and
understand the texts will make it possible for me to follow along.
William
--
Sphinx of black quartz, judge my vow.
https://designinto3d.com/
I'm not sure I understand your goal. Here's a couple references:
https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/notes.html
https://pomax.github.io/bezierinfo/
Both of these methods are ways of using control points to specify a curve.
In the case of beziers the control points globally alter the curve. In the
case of B-splines the control points have a local effect whose "distance"
depends on the degree.
On Sun, Aug 11, 2024 at 9:52 AM William F. Adams <willadams@aol.com> wrote:
> I am not qualified to evaluate which mathematical representation is better
> or even what advantages or disadvantages each has. (will gladly accept
> reading lists which might help me understand such discussions)
>
> It is my hope that I can wrap my mind around this code and use it to
> generalize a mechanism where a series of 2D spline is both output as a
> series of short lines (where multiple iterations of a tool are hull()ed
> together so as to show the effect of a cutting tool and at the same time
> represent the same spline as a series of arcs and lines in a matching DXF.
>
> Folks who are curious as to this context may see:
>
> https://github.com/WillAdams/gcodepreview/blob/main/gcodepreview.pdf
>
> which I believe is approaching a usable state for cutting lines and arcs
> (though now that I write that I wonder if I should do inside and outside
> DXF arcs for a given arc toolpath).
>
> Anyway if anyone wants to discuss this aspect, please create a new e-mail
> thread, and please preface it with a reading list which once I read and
> understand the texts will make it possible for me to follow along.
>
> William
>
> --
> Sphinx of black quartz, judge my vow.
> https://designinto3d.com/
>

WF
William F. Adams
Sun, Aug 11, 2024 2:58 PM
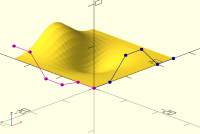
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control points each) with 2 methods
- converted both lines to bspline curves and created a surface by adding the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small surface with only 400 points overall
That is exactly the sort of thing I was reaching for when I wrote the below, and I thank you for validating that.
William
\subsubsection{Bézier curves in 3 dimensions}
One question is how many Bézier curves would it be necessary to have to define a surface
in 3 dimensions. Attributes for this which are desirable/necessary:
\begin{itemize}
\item concise --- a given Bézier curve should be represented by just the point coordinates,
so two on-curve points, two off-curve points, each with a pair of coordinates
\item For a given shape/region it will need to be possible to have a matching definition
exactly match up with it so that one could piece together a larger more complex shape
from smaller/simpler regions
\item similarly it will be necessary for it to be possible to sub-divide a defined region ---
for example it should be possible if one had 4 adjacent regions, then the four quadrants
at the intersection of the four regions could be used to construct a new region --- is it
possible to derive a new Bézier curve from half of two other curves?
\end{itemize}
\begin{samepage}
For the three planes:
\begin{itemize}
\item XY
\item XZ
\item ZY
\end{itemize}
\noindent it should be possible to have three Bézier curves (left-most/right-most or front-back or
top/bottom for two, and a mid-line for the third), so a region which can be so represented would
be definable by:
\begin{verbatim}
3 planes * 3 Béziers * (2 on-curve + 2 off-curve points) == 36 coordinate pairs
\end{verbatim}
\end{samepage}
\noindent which is a marked contrast to representations such as:
\url{https://github.com/DavidPhillipOster/Teapot}
\noindent and regions which could not be so represented could be sub-divided until the
representation is workable.
On Sunday, August 11, 2024 at 09:35:30 AM EDT, Sanjeev Prabhakar via Discuss <discuss@lists.openscad.org> wrote:
>I did a small test of efficiency
>
>following surface is created using 2 lines (blue and magenta, 6 control points each) with 2 methods
>1. converted both lines to bspline curves and created a surface by adding the points (time: 0.015s)
>2. by directly using the formula for bspline surface (time: 0.53s)
>
>method 1 is around 35 times faster.
>
>Maybe the algorithm written is not efficient, but this is a very small surface with only 400 points overall
That is exactly the sort of thing I was reaching for when I wrote the below, and I thank you for validating that.
William
\subsubsection{Bézier curves in 3 dimensions}
One question is how many Bézier curves would it be necessary to have to define a surface
in 3 dimensions. Attributes for this which are desirable/necessary:
\begin{itemize}
\item concise --- a given Bézier curve should be represented by just the point coordinates,
so two on-curve points, two off-curve points, each with a pair of coordinates
\item For a given shape/region it will need to be possible to have a matching definition
exactly match up with it so that one could piece together a larger more complex shape
from smaller/simpler regions
\item similarly it will be necessary for it to be possible to sub-divide a defined region ---
for example it should be possible if one had 4 adjacent regions, then the four quadrants
at the intersection of the four regions could be used to construct a new region --- is it
possible to derive a new Bézier curve from half of two other curves?
\end{itemize}
\begin{samepage}
For the three planes:
\begin{itemize}
\item XY
\item XZ
\item ZY
\end{itemize}
\noindent it should be possible to have three Bézier curves (left-most/right-most or front-back or
top/bottom for two, and a mid-line for the third), so a region which can be so represented would
be definable by:
\begin{verbatim}
3 planes * 3 Béziers * (2 on-curve + 2 off-curve points) == 36 coordinate pairs
\end{verbatim}
\end{samepage}
\noindent which is a marked contrast to representations such as:
\url{https://github.com/DavidPhillipOster/Teapot}
\noindent and regions which could not be so represented could be sub-divided until the
representation is workable.


SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 3:05 PM
Hi William,
Bezier is much simpler to write mathematically.
There is Bernstein polynomial equation which is similar to calculating like
(a+b)^2 .... or up to (a+b)^n where n is the degree of polynomial.
So how do you calculate (a+b)^2 or for that matter to any polynomial degree
n
an integer i => 0 to n calculates each term of the above equation
n!/(i! * (n-i)!)a^ib^(n-i) where n! means factorial of n --equation 1
substituting a=t and b=(1-t)
where t is a parameter which goes from 0 ->1 and you can have any numbers
within that range
in bezier the degree of the curve is 1 less than the control points e.g. if
you have 10 control points the polynomial degree will be 9.
so finally equation for bezier is:
sum(p[i]*n!/(i! * (n-i)!)t^i(1-t)^(n-i)) where p[i] is the ith control
point
my simple 6 lines function for bezier curve is following:
def bezier(p,s=10):
'''
bezier curve defined by points 'p' and number of segments 's'
'''
p=a_(p)
n=len(p)
k=n-1
f=[[p[i]*comb(k,i)u**i(1-u)**(k-i) for i in range(n)]
for u in linspace(0,1,s)]
p1=l_(a_([p.sum(0) for p in a_(f)]))
return p1
On Sun, 11 Aug 2024 at 19:22, William F. Adams via Discuss <
discuss@lists.openscad.org> wrote:
I am not qualified to evaluate which mathematical representation is better
or even what advantages or disadvantages each has. (will gladly accept
reading lists which might help me understand such discussions)
It is my hope that I can wrap my mind around this code and use it to
generalize a mechanism where a series of 2D spline is both output as a
series of short lines (where multiple iterations of a tool are hull()ed
together so as to show the effect of a cutting tool and at the same time
represent the same spline as a series of arcs and lines in a matching DXF.
Folks who are curious as to this context may see:
https://github.com/WillAdams/gcodepreview/blob/main/gcodepreview.pdf
which I believe is approaching a usable state for cutting lines and arcs
(though now that I write that I wonder if I should do inside and outside
DXF arcs for a given arc toolpath).
Anyway if anyone wants to discuss this aspect, please create a new e-mail
thread, and please preface it with a reading list which once I read and
understand the texts will make it possible for me to follow along.
William
--
Sphinx of black quartz, judge my vow.
https://designinto3d.com/
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Hi William,
Bezier is much simpler to write mathematically.
There is Bernstein polynomial equation which is similar to calculating like
(a+b)^2 .... or up to (a+b)^n where n is the degree of polynomial.
So how do you calculate (a+b)^2 or for that matter to any polynomial degree
n
an integer i => 0 to n calculates each term of the above equation
n!/(i! * (n-i)!)*a^i*b^(n-i) where n! means factorial of n --equation 1
substituting a=t and b=(1-t)
where t is a parameter which goes from 0 ->1 and you can have any numbers
within that range
in bezier the degree of the curve is 1 less than the control points e.g. if
you have 10 control points the polynomial degree will be 9.
so finally equation for bezier is:
sum(p[i]*n!/(i! * (n-i)!)*t^i*(1-t)^(n-i)) where p[i] is the ith control
point
my simple 6 lines function for bezier curve is following:
def bezier(p,s=10):
'''
bezier curve defined by points 'p' and number of segments 's'
'''
p=a_(p)
n=len(p)
k=n-1
f=[[p[i]*comb(k,i)*u**i*(1-u)**(k-i) for i in range(n)]
for u in linspace(0,1,s)]
p1=l_(a_([p.sum(0) for p in a_(f)]))
return p1
On Sun, 11 Aug 2024 at 19:22, William F. Adams via Discuss <
discuss@lists.openscad.org> wrote:
> I am not qualified to evaluate which mathematical representation is better
> or even what advantages or disadvantages each has. (will gladly accept
> reading lists which might help me understand such discussions)
>
> It is my hope that I can wrap my mind around this code and use it to
> generalize a mechanism where a series of 2D spline is both output as a
> series of short lines (where multiple iterations of a tool are hull()ed
> together so as to show the effect of a cutting tool and at the same time
> represent the same spline as a series of arcs and lines in a matching DXF.
>
> Folks who are curious as to this context may see:
>
> https://github.com/WillAdams/gcodepreview/blob/main/gcodepreview.pdf
>
> which I believe is approaching a usable state for cutting lines and arcs
> (though now that I write that I wonder if I should do inside and outside
> DXF arcs for a given arc toolpath).
>
> Anyway if anyone wants to discuss this aspect, please create a new e-mail
> thread, and please preface it with a reading list which once I read and
> understand the texts will make it possible for me to follow along.
>
> William
>
> --
> Sphinx of black quartz, judge my vow.
> https://designinto3d.com/
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

WF
William F. Adams
Sun, Aug 11, 2024 3:09 PM
On Sunday, August 11, 2024 at 10:40:03 AM EDT, Adrian Mariano avm4@cornell.edu wrote:
My thanks. I had found those previously, but have now made specific note of them.
Let me turn this around a bit.
Imagine if OpenSCAD had been written as a Literate Program: https://www.goodreads.com/review/list/21394355-william-adams?ref=nav_mybooks&shelf=literateprograms --- and if at the back of that listing, or during the course of writing all that code there were various footnotes to books which explained in further detail the various mathematical and geometric and trigonometric principles involved --- what would those books be?
I've been working on a list of books related to CNC concepts/principles, some of which relate to geometry and so forth:
https://www.goodreads.com/review/list/21394355-william-adams?ref=nav_mybooks&shelf=cnc
what additional books would I need to read and understand so as to be able to "grok" the underlying concepts of code such as Sanjeev Prabhakar has been very generously sharing with us?
William
--
Sphinx of black quartz, judge my vow.
https://designinto3d.com/
On Sunday, August 11, 2024 at 10:40:03 AM EDT, Adrian Mariano <avm4@cornell.edu> wrote:
>I'm not sure I understand your goal. Here's a couple references:
>
>https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/notes.html
>https://pomax.github.io/bezierinfo/
>
>Both of these methods are ways of using control points to specify a curve.
>In the case of beziers the control points globally alter the curve. In the case of
>B-splines the control points have a local effect whose "distance" depends on the degree.
My thanks. I had found those previously, but have now made specific note of them.
Let me turn this around a bit.
Imagine if OpenSCAD had been written as a Literate Program: https://www.goodreads.com/review/list/21394355-william-adams?ref=nav_mybooks&shelf=literateprograms --- and if at the back of that listing, or during the course of writing all that code there were various footnotes to books which explained in further detail the various mathematical and geometric and trigonometric principles involved --- what would those books be?
I've been working on a list of books related to CNC concepts/principles, some of which relate to geometry and so forth:
https://www.goodreads.com/review/list/21394355-william-adams?ref=nav_mybooks&shelf=cnc
what additional books would I need to read and understand so as to be able to "grok" the underlying concepts of code such as Sanjeev Prabhakar has been very generously sharing with us?
William
--
Sphinx of black quartz, judge my vow.
https://designinto3d.com/

SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 3:14 PM
I think the basis function in bspline consumes most of the time as it
checks the condition if parameter value lies with in 2 consecutive knots
and switches 1 or 0.
In case of 2 lines method it is checked only sum of 2 bspline line points
whereas in case of surface it gets multiplied and therefore such
inefficiency
On Sun, 11 Aug 2024 at 20:05, Adrian Mariano avm4@cornell.edu wrote:
I am not sure I understand what method 1 is. A surface could easily
require 100 points along each edge, which means 10k points in total. I
know that for bezier surfaces run time was a concern. It got slow with
surfaces that had a lot of points, and since the bezier calculations cannot
be cached you take that run-time hit every time you do anything with your
model, so run time performance was important. Implementing beziers using
matrix multiplication was a 10x-20x speed improvement compared to
recursively using the de casteljau algorithm. The problem with b-splines
is that the knots create a bunch of variability in the structure of the
shape. I guess your implementation assumes uniformly spaced knots?
On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
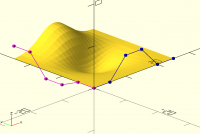
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control
points each) with 2 methods
- converted both lines to bspline curves and created a surface by adding
the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or maybe
use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I
need to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
I think the basis function in bspline consumes most of the time as it
checks the condition if parameter value lies with in 2 consecutive knots
and switches 1 or 0.
In case of 2 lines method it is checked only sum of 2 bspline line points
whereas in case of surface it gets multiplied and therefore such
inefficiency
On Sun, 11 Aug 2024 at 20:05, Adrian Mariano <avm4@cornell.edu> wrote:
> I am not sure I understand what method 1 is. A surface could easily
> require 100 points along each edge, which means 10k points in total. I
> know that for bezier surfaces run time *was* a concern. It got slow with
> surfaces that had a lot of points, and since the bezier calculations cannot
> be cached you take that run-time hit every time you do anything with your
> model, so run time performance was important. Implementing beziers using
> matrix multiplication was a 10x-20x speed improvement compared to
> recursively using the de casteljau algorithm. The problem with b-splines
> is that the knots create a bunch of variability in the structure of the
> shape. I guess your implementation assumes uniformly spaced knots?
>
> On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
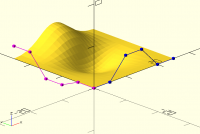
>> I did a small test of efficiency
>>
>> following surface is created using 2 lines (blue and magenta, 6 control
>> points each) with 2 methods
>> 1. converted both lines to bspline curves and created a surface by adding
>> the points (time: 0.015s)
>> 2. by directly using the formula for bspline surface (time: 0.53s)
>>
>> method 1 is around 35 times faster.
>>
>> Maybe the algorithm written is not efficient, but this is a very small
>> surface with only 400 points overall
>>
>> [image: Screenshot 2024-08-11 at 6.55.26 PM.png]
>>
>> On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>>> What better ways than bspline exist for creating surfaces? I had the
>>> impression that NURBS were the tool for this out in the big world, and they
>>> are just a slight generalization of bspline. I'm planning and
>>> implementation of bspline/NURBS at some point, but efficient implementation
>>> in OpenSCAD may be difficult, compared to beziers, which can be done very
>>> fast as a matrix multiply.
>>>
>>> On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> To create surfaces there are better ways than bspline I suppose.
>>>> It is mainly useful for creating smoother paths for extruding or maybe
>>>> use for creating surfaces separately.
>>>>
>>>> creating a closed section from a list will surely be very useful. I
>>>> need to check the application in various cases.
>>>>
>>>> Few days back I created a model of car seat, there it should be much
>>>> easier if bspline is used instead of bezier
>>>>
>>>

AM
Adrian Mariano
Sun, Aug 11, 2024 6:42 PM
Part of the challenge in implementing b splines is devising the right
interface. A request came in that BOSL2 add b splines to help with
exporting stuff from some other cad software (freecad, maybe?), and I
looked it over to understand the API. From your description above, it
sounds like you're doing non-uniform b-splines. But it sounds like nobody
uses those---they provide little benefit over uniform b-splines. With
uniform b-splines---possibly with non-unity knot multiplicity----it's easy
to compute the correct knot index to associate with a parameter value. The
API seems to be giving just a vector of multiplicities, since knot spacing
is assumed uniform.
It sounds like you evaluate the basis functions instead of directly
computing the bspline points? I wonder about the advantage of doing it
that way. Most sources seem to suggest computing the points directly
without ever computing the basis functions. I have written a function
that works that way. There is nothing I can point at as "the reason this
would be slow" other than it being a quadratic algorithm implemented by
recursion, which is kinda slow in OpenSCAD.
On Sun, Aug 11, 2024 at 11:14 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I think the basis function in bspline consumes most of the time as it
checks the condition if parameter value lies with in 2 consecutive knots
and switches 1 or 0.
In case of 2 lines method it is checked only sum of 2 bspline line points
whereas in case of surface it gets multiplied and therefore such
inefficiency
On Sun, 11 Aug 2024 at 20:05, Adrian Mariano avm4@cornell.edu wrote:
I am not sure I understand what method 1 is. A surface could easily
require 100 points along each edge, which means 10k points in total. I
know that for bezier surfaces run time was a concern. It got slow with
surfaces that had a lot of points, and since the bezier calculations cannot
be cached you take that run-time hit every time you do anything with your
model, so run time performance was important. Implementing beziers using
matrix multiplication was a 10x-20x speed improvement compared to
recursively using the de casteljau algorithm. The problem with b-splines
is that the knots create a bunch of variability in the structure of the
shape. I guess your implementation assumes uniformly spaced knots?
On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control
points each) with 2 methods
- converted both lines to bspline curves and created a surface by
adding the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or
maybe use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I
need to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
Part of the challenge in implementing b splines is devising the right
interface. A request came in that BOSL2 add b splines to help with
exporting stuff from some other cad software (freecad, maybe?), and I
looked it over to understand the API. From your description above, it
sounds like you're doing non-uniform b-splines. But it sounds like nobody
uses those---they provide little benefit over uniform b-splines. With
uniform b-splines---possibly with non-unity knot multiplicity----it's easy
to compute the correct knot index to associate with a parameter value. The
API seems to be giving just a vector of multiplicities, since knot spacing
is assumed uniform.
It sounds like you evaluate the basis functions instead of directly
computing the bspline points? I wonder about the advantage of doing it
that way. Most sources seem to suggest computing the points directly
without ever computing the basis functions. I have written a function
that works that way. There is nothing I can point at as "the reason this
would be slow" other than it being a quadratic algorithm implemented by
recursion, which is kinda slow in OpenSCAD.
On Sun, Aug 11, 2024 at 11:14 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I think the basis function in bspline consumes most of the time as it
> checks the condition if parameter value lies with in 2 consecutive knots
> and switches 1 or 0.
>
> In case of 2 lines method it is checked only sum of 2 bspline line points
>
> whereas in case of surface it gets multiplied and therefore such
> inefficiency
>
> On Sun, 11 Aug 2024 at 20:05, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> I am not sure I understand what method 1 is. A surface could easily
>> require 100 points along each edge, which means 10k points in total. I
>> know that for bezier surfaces run time *was* a concern. It got slow with
>> surfaces that had a lot of points, and since the bezier calculations cannot
>> be cached you take that run-time hit every time you do anything with your
>> model, so run time performance was important. Implementing beziers using
>> matrix multiplication was a 10x-20x speed improvement compared to
>> recursively using the de casteljau algorithm. The problem with b-splines
>> is that the knots create a bunch of variability in the structure of the
>> shape. I guess your implementation assumes uniformly spaced knots?
>>
>> On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> I did a small test of efficiency
>>>
>>> following surface is created using 2 lines (blue and magenta, 6 control
>>> points each) with 2 methods
>>> 1. converted both lines to bspline curves and created a surface by
>>> adding the points (time: 0.015s)
>>> 2. by directly using the formula for bspline surface (time: 0.53s)
>>>
>>> method 1 is around 35 times faster.
>>>
>>> Maybe the algorithm written is not efficient, but this is a very small
>>> surface with only 400 points overall
>>>
>>> [image: Screenshot 2024-08-11 at 6.55.26 PM.png]
>>>
>>> On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> What better ways than bspline exist for creating surfaces? I had the
>>>> impression that NURBS were the tool for this out in the big world, and they
>>>> are just a slight generalization of bspline. I'm planning and
>>>> implementation of bspline/NURBS at some point, but efficient implementation
>>>> in OpenSCAD may be difficult, compared to beziers, which can be done very
>>>> fast as a matrix multiply.
>>>>
>>>> On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
>>>> discuss@lists.openscad.org> wrote:
>>>>
>>>>> To create surfaces there are better ways than bspline I suppose.
>>>>> It is mainly useful for creating smoother paths for extruding or
>>>>> maybe use for creating surfaces separately.
>>>>>
>>>>> creating a closed section from a list will surely be very useful. I
>>>>> need to check the application in various cases.
>>>>>
>>>>> Few days back I created a model of car seat, there it should be much
>>>>> easier if bspline is used instead of bezier
>>>>>
>>>>

SP
Sanjeev Prabhakar
Sun, Aug 11, 2024 11:05 PM
I have calculated uniform bspline and you can check the algorithm in the
file dependencies.scad
Whatever way you calculate it you need to find whether the current
parameter is within which knots.
To do an open bspline you have to clamp the spline at both ends and
accordingly the knots needs to be defined.
If the number of points are higher and degree is higher it becomes quite
slow in my case.
On Mon, 12 Aug, 2024, 12:12 am Adrian Mariano, avm4@cornell.edu wrote:
Part of the challenge in implementing b splines is devising the right
interface. A request came in that BOSL2 add b splines to help with
exporting stuff from some other cad software (freecad, maybe?), and I
looked it over to understand the API. From your description above, it
sounds like you're doing non-uniform b-splines. But it sounds like nobody
uses those---they provide little benefit over uniform b-splines. With
uniform b-splines---possibly with non-unity knot multiplicity----it's easy
to compute the correct knot index to associate with a parameter value. The
API seems to be giving just a vector of multiplicities, since knot spacing
is assumed uniform.
It sounds like you evaluate the basis functions instead of directly
computing the bspline points? I wonder about the advantage of doing it
that way. Most sources seem to suggest computing the points directly
without ever computing the basis functions. I have written a function
that works that way. There is nothing I can point at as "the reason this
would be slow" other than it being a quadratic algorithm implemented by
recursion, which is kinda slow in OpenSCAD.
On Sun, Aug 11, 2024 at 11:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I think the basis function in bspline consumes most of the time as it
checks the condition if parameter value lies with in 2 consecutive knots
and switches 1 or 0.
In case of 2 lines method it is checked only sum of 2 bspline line points
whereas in case of surface it gets multiplied and therefore such
inefficiency
On Sun, 11 Aug 2024 at 20:05, Adrian Mariano avm4@cornell.edu wrote:
I am not sure I understand what method 1 is. A surface could easily
require 100 points along each edge, which means 10k points in total. I
know that for bezier surfaces run time was a concern. It got slow with
surfaces that had a lot of points, and since the bezier calculations cannot
be cached you take that run-time hit every time you do anything with your
model, so run time performance was important. Implementing beziers using
matrix multiplication was a 10x-20x speed improvement compared to
recursively using the de casteljau algorithm. The problem with b-splines
is that the knots create a bunch of variability in the structure of the
shape. I guess your implementation assumes uniformly spaced knots?
On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6 control
points each) with 2 methods
- converted both lines to bspline curves and created a surface by
adding the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or
maybe use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I
need to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
I have calculated uniform bspline and you can check the algorithm in the
file dependencies.scad
Whatever way you calculate it you need to find whether the current
parameter is within which knots.
To do an open bspline you have to clamp the spline at both ends and
accordingly the knots needs to be defined.
If the number of points are higher and degree is higher it becomes quite
slow in my case.
On Mon, 12 Aug, 2024, 12:12 am Adrian Mariano, <avm4@cornell.edu> wrote:
> Part of the challenge in implementing b splines is devising the right
> interface. A request came in that BOSL2 add b splines to help with
> exporting stuff from some other cad software (freecad, maybe?), and I
> looked it over to understand the API. From your description above, it
> sounds like you're doing non-uniform b-splines. But it sounds like nobody
> uses those---they provide little benefit over uniform b-splines. With
> uniform b-splines---possibly with non-unity knot multiplicity----it's easy
> to compute the correct knot index to associate with a parameter value. The
> API seems to be giving just a vector of multiplicities, since knot spacing
> is assumed uniform.
>
> It sounds like you evaluate the basis functions instead of directly
> computing the bspline points? I wonder about the advantage of doing it
> that way. Most sources seem to suggest computing the points directly
> without ever computing the basis functions. I have written a function
> that works that way. There is nothing I can point at as "the reason this
> would be slow" other than it being a quadratic algorithm implemented by
> recursion, which is kinda slow in OpenSCAD.
>
> On Sun, Aug 11, 2024 at 11:14 AM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> I think the basis function in bspline consumes most of the time as it
>> checks the condition if parameter value lies with in 2 consecutive knots
>> and switches 1 or 0.
>>
>> In case of 2 lines method it is checked only sum of 2 bspline line points
>>
>> whereas in case of surface it gets multiplied and therefore such
>> inefficiency
>>
>> On Sun, 11 Aug 2024 at 20:05, Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> I am not sure I understand what method 1 is. A surface could easily
>>> require 100 points along each edge, which means 10k points in total. I
>>> know that for bezier surfaces run time *was* a concern. It got slow with
>>> surfaces that had a lot of points, and since the bezier calculations cannot
>>> be cached you take that run-time hit every time you do anything with your
>>> model, so run time performance was important. Implementing beziers using
>>> matrix multiplication was a 10x-20x speed improvement compared to
>>> recursively using the de casteljau algorithm. The problem with b-splines
>>> is that the knots create a bunch of variability in the structure of the
>>> shape. I guess your implementation assumes uniformly spaced knots?
>>>
>>> On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> I did a small test of efficiency
>>>>
>>>> following surface is created using 2 lines (blue and magenta, 6 control
>>>> points each) with 2 methods
>>>> 1. converted both lines to bspline curves and created a surface by
>>>> adding the points (time: 0.015s)
>>>> 2. by directly using the formula for bspline surface (time: 0.53s)
>>>>
>>>> method 1 is around 35 times faster.
>>>>
>>>> Maybe the algorithm written is not efficient, but this is a very small
>>>> surface with only 400 points overall
>>>>
>>>> [image: Screenshot 2024-08-11 at 6.55.26 PM.png]
>>>>
>>>> On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
>>>> discuss@lists.openscad.org> wrote:
>>>>
>>>>> What better ways than bspline exist for creating surfaces? I had the
>>>>> impression that NURBS were the tool for this out in the big world, and they
>>>>> are just a slight generalization of bspline. I'm planning and
>>>>> implementation of bspline/NURBS at some point, but efficient implementation
>>>>> in OpenSCAD may be difficult, compared to beziers, which can be done very
>>>>> fast as a matrix multiply.
>>>>>
>>>>> On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
>>>>> discuss@lists.openscad.org> wrote:
>>>>>
>>>>>> To create surfaces there are better ways than bspline I suppose.
>>>>>> It is mainly useful for creating smoother paths for extruding or
>>>>>> maybe use for creating surfaces separately.
>>>>>>
>>>>>> creating a closed section from a list will surely be very useful. I
>>>>>> need to check the application in various cases.
>>>>>>
>>>>>> Few days back I created a model of car seat, there it should be much
>>>>>> easier if bspline is used instead of bezier
>>>>>>
>>>>>

AM
Adrian Mariano
Sun, Aug 11, 2024 11:42 PM
I'm having some confusion with the clamped case where I have a knot
multiplicity (at the ends) that is higher than the degree. This case isn't
really addressed by the formula I was using. I'm also not sure how you
clamp if you don't have very many control points. With degree p and n
control points you have p+n+1 knots but if you need p+1 multiplicity at
each end then if n is too small it's impossible.
I am also hazy also about the closed case. You are supposed to duplicate p
control points, but I don't understand how to handle the knots.
You need to find which knot interval the current parameter lies within.
This can be done for the uniform case by floor(u/(knotcount-1)), which is
not a slow calculation. If you have non-unity multiplicities then you can
use a slightly more complex calculation but it will still be fast.
My code is currently taking about 1s to compute 1000 points on a b-spline
with 100 control points and degree 7. Degree 3 is 0.9 s. Degree 16 is
1.1s. So it doesn't seem very sensitive to degree, nor horribly slow. (My
computer is pretty fast.)
On Sun, Aug 11, 2024 at 7:05 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I have calculated uniform bspline and you can check the algorithm in the
file dependencies.scad
Whatever way you calculate it you need to find whether the current
parameter is within which knots.
To do an open bspline you have to clamp the spline at both ends and
accordingly the knots needs to be defined.
If the number of points are higher and degree is higher it becomes quite
slow in my case.
On Mon, 12 Aug, 2024, 12:12 am Adrian Mariano, avm4@cornell.edu wrote:
Part of the challenge in implementing b splines is devising the right
interface. A request came in that BOSL2 add b splines to help with
exporting stuff from some other cad software (freecad, maybe?), and I
looked it over to understand the API. From your description above, it
sounds like you're doing non-uniform b-splines. But it sounds like nobody
uses those---they provide little benefit over uniform b-splines. With
uniform b-splines---possibly with non-unity knot multiplicity----it's easy
to compute the correct knot index to associate with a parameter value. The
API seems to be giving just a vector of multiplicities, since knot spacing
is assumed uniform.
It sounds like you evaluate the basis functions instead of directly
computing the bspline points? I wonder about the advantage of doing it
that way. Most sources seem to suggest computing the points directly
without ever computing the basis functions. I have written a function
that works that way. There is nothing I can point at as "the reason this
would be slow" other than it being a quadratic algorithm implemented by
recursion, which is kinda slow in OpenSCAD.
On Sun, Aug 11, 2024 at 11:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I think the basis function in bspline consumes most of the time as it
checks the condition if parameter value lies with in 2 consecutive knots
and switches 1 or 0.
In case of 2 lines method it is checked only sum of 2 bspline line points
whereas in case of surface it gets multiplied and therefore such
inefficiency
On Sun, 11 Aug 2024 at 20:05, Adrian Mariano avm4@cornell.edu wrote:
I am not sure I understand what method 1 is. A surface could easily
require 100 points along each edge, which means 10k points in total. I
know that for bezier surfaces run time was a concern. It got slow with
surfaces that had a lot of points, and since the bezier calculations cannot
be cached you take that run-time hit every time you do anything with your
model, so run time performance was important. Implementing beziers using
matrix multiplication was a 10x-20x speed improvement compared to
recursively using the de casteljau algorithm. The problem with b-splines
is that the knots create a bunch of variability in the structure of the
shape. I guess your implementation assumes uniformly spaced knots?
On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I did a small test of efficiency
following surface is created using 2 lines (blue and magenta, 6
control points each) with 2 methods
- converted both lines to bspline curves and created a surface by
adding the points (time: 0.015s)
- by directly using the formula for bspline surface (time: 0.53s)
method 1 is around 35 times faster.
Maybe the algorithm written is not efficient, but this is a very small
surface with only 400 points overall
[image: Screenshot 2024-08-11 at 6.55.26 PM.png]
On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
What better ways than bspline exist for creating surfaces? I had the
impression that NURBS were the tool for this out in the big world, and they
are just a slight generalization of bspline. I'm planning and
implementation of bspline/NURBS at some point, but efficient implementation
in OpenSCAD may be difficult, compared to beziers, which can be done very
fast as a matrix multiply.
On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
To create surfaces there are better ways than bspline I suppose.
It is mainly useful for creating smoother paths for extruding or
maybe use for creating surfaces separately.
creating a closed section from a list will surely be very useful. I
need to check the application in various cases.
Few days back I created a model of car seat, there it should be much
easier if bspline is used instead of bezier
I'm having some confusion with the clamped case where I have a knot
multiplicity (at the ends) that is higher than the degree. This case isn't
really addressed by the formula I was using. I'm also not sure how you
clamp if you don't have very many control points. With degree p and n
control points you have p+n+1 knots but if you need p+1 multiplicity at
each end then if n is too small it's impossible.
I am also hazy also about the closed case. You are supposed to duplicate p
control points, but I don't understand how to handle the knots.
You need to find which knot interval the current parameter lies within.
This can be done for the uniform case by floor(u/(knotcount-1)), which is
not a slow calculation. If you have non-unity multiplicities then you can
use a slightly more complex calculation but it will still be fast.
My code is currently taking about 1s to compute 1000 points on a b-spline
with 100 control points and degree 7. Degree 3 is 0.9 s. Degree 16 is
1.1s. So it doesn't seem very sensitive to degree, nor horribly slow. (My
computer is pretty fast.)
On Sun, Aug 11, 2024 at 7:05 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I have calculated uniform bspline and you can check the algorithm in the
> file dependencies.scad
>
> Whatever way you calculate it you need to find whether the current
> parameter is within which knots.
>
> To do an open bspline you have to clamp the spline at both ends and
> accordingly the knots needs to be defined.
>
> If the number of points are higher and degree is higher it becomes quite
> slow in my case.
>
> On Mon, 12 Aug, 2024, 12:12 am Adrian Mariano, <avm4@cornell.edu> wrote:
>
>> Part of the challenge in implementing b splines is devising the right
>> interface. A request came in that BOSL2 add b splines to help with
>> exporting stuff from some other cad software (freecad, maybe?), and I
>> looked it over to understand the API. From your description above, it
>> sounds like you're doing non-uniform b-splines. But it sounds like nobody
>> uses those---they provide little benefit over uniform b-splines. With
>> uniform b-splines---possibly with non-unity knot multiplicity----it's easy
>> to compute the correct knot index to associate with a parameter value. The
>> API seems to be giving just a vector of multiplicities, since knot spacing
>> is assumed uniform.
>>
>> It sounds like you evaluate the basis functions instead of directly
>> computing the bspline points? I wonder about the advantage of doing it
>> that way. Most sources seem to suggest computing the points directly
>> without ever computing the basis functions. I have written a function
>> that works that way. There is nothing I can point at as "the reason this
>> would be slow" other than it being a quadratic algorithm implemented by
>> recursion, which is kinda slow in OpenSCAD.
>>
>> On Sun, Aug 11, 2024 at 11:14 AM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> I think the basis function in bspline consumes most of the time as it
>>> checks the condition if parameter value lies with in 2 consecutive knots
>>> and switches 1 or 0.
>>>
>>> In case of 2 lines method it is checked only sum of 2 bspline line points
>>>
>>> whereas in case of surface it gets multiplied and therefore such
>>> inefficiency
>>>
>>> On Sun, 11 Aug 2024 at 20:05, Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> I am not sure I understand what method 1 is. A surface could easily
>>>> require 100 points along each edge, which means 10k points in total. I
>>>> know that for bezier surfaces run time *was* a concern. It got slow with
>>>> surfaces that had a lot of points, and since the bezier calculations cannot
>>>> be cached you take that run-time hit every time you do anything with your
>>>> model, so run time performance was important. Implementing beziers using
>>>> matrix multiplication was a 10x-20x speed improvement compared to
>>>> recursively using the de casteljau algorithm. The problem with b-splines
>>>> is that the knots create a bunch of variability in the structure of the
>>>> shape. I guess your implementation assumes uniformly spaced knots?
>>>>
>>>> On Sun, Aug 11, 2024 at 9:35 AM Sanjeev Prabhakar <
>>>> sprabhakar2006@gmail.com> wrote:
>>>>
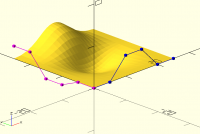
>>>>> I did a small test of efficiency
>>>>>
>>>>> following surface is created using 2 lines (blue and magenta, 6
>>>>> control points each) with 2 methods
>>>>> 1. converted both lines to bspline curves and created a surface by
>>>>> adding the points (time: 0.015s)
>>>>> 2. by directly using the formula for bspline surface (time: 0.53s)
>>>>>
>>>>> method 1 is around 35 times faster.
>>>>>
>>>>> Maybe the algorithm written is not efficient, but this is a very small
>>>>> surface with only 400 points overall
>>>>>
>>>>> [image: Screenshot 2024-08-11 at 6.55.26 PM.png]
>>>>>
>>>>> On Sun, 11 Aug 2024 at 18:41, Adrian Mariano via Discuss <
>>>>> discuss@lists.openscad.org> wrote:
>>>>>
>>>>>> What better ways than bspline exist for creating surfaces? I had the
>>>>>> impression that NURBS were the tool for this out in the big world, and they
>>>>>> are just a slight generalization of bspline. I'm planning and
>>>>>> implementation of bspline/NURBS at some point, but efficient implementation
>>>>>> in OpenSCAD may be difficult, compared to beziers, which can be done very
>>>>>> fast as a matrix multiply.
>>>>>>
>>>>>> On Sun, Aug 11, 2024 at 9:02 AM Sanjeev Prabhakar via Discuss <
>>>>>> discuss@lists.openscad.org> wrote:
>>>>>>
>>>>>>> To create surfaces there are better ways than bspline I suppose.
>>>>>>> It is mainly useful for creating smoother paths for extruding or
>>>>>>> maybe use for creating surfaces separately.
>>>>>>>
>>>>>>> creating a closed section from a list will surely be very useful. I
>>>>>>> need to check the application in various cases.
>>>>>>>
>>>>>>> Few days back I created a model of car seat, there it should be much
>>>>>>> easier if bspline is used instead of bezier
>>>>>>>
>>>>>>