Re: Provide a simple measurement tool
Going back to my original bit of code with the two cones, I would like
to be able to calculate the xyz coordinates of this cone tip. (it being
60 years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are
fond of doing everything from first principles every time, which makes
them more painful than might be necessary. But my quick solution to
your squares problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1),
select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed
definitions of points are, the "random" points. Your definitions both
have to do with optimization, which means you've gone up a leap in
complexity from simple geometry. Points derived from optimization
aren't going to be clickable on a model. You can't "see" them. The
only way you can find these points is by doing the math.
I can't run your model because it's full of parameters. But I would
think that in that case, at least, it would be possible to define your
model in terms of the width. If you start from the width and build
everything from there then you'll have the right width. That's the
kind of thing I meant when I wondered about the need for access to
distance values. The notion that you need to know the width of your
model after the fact so you can fix your botched model by trial and
error to make it the right width....doesn't appeal to me as a design
strategy. But if you really want to pursue trial-and-error design
then having a way to measure does seem very important. (It's unclear
to me if starting from the width just shifts the measurement problem
somewhere else, but it seems like if you have measurable parameters
you should be able to measure them and then design to the measurements
directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown
<openscad@jordan.maileater.net mailto:openscad@jordan.maileater.net>
wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a point
is? What are you trying to do that requires this knowledge in a
real model? I wonder if there might be alternative approaches
that don't require that information, or where the model can be
structured so that it's easy to know where the point is. I
suspect that at least some of the time, such alternative
approaches may exist.
I think the problem with straight "calculation" schemes is that
they can get very hard, very fast.
Quick, what's the distance between the closest points in these
squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can do
that off the top of your head, but it would take me some pretty
serious thinking. And that's a simple case.
In a real project... as I've mentioned, a lot of my work is in
scale models. I was designing an armchair:
https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true, open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch);
}
}
All of those dimensions are measured by hand off the real object,
and the angles are eyeballed.
Now, what's the width, measured between the outsides of the two
arms? I want to tweak the angles and sizes so that's it's pretty
close to correct.
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
Hi Ray,
I don't see a cone?
https://www.dropbox.com/s/h7erjxuqa4ny9lq/RayCone.jpg?raw=1
Terry
====================
On Tue, 31 Aug 2021 13:42:25 +0100, you wrote:
Going back to my original bit of code with the two cones, I would like
to be able to calculate the xyz coordinates of this cone tip. (it being
60 years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are
fond of doing everything from first principles every time, which makes
them more painful than might be necessary. But my quick solution to
your squares problem:sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1),
select(sq2,j,j+1))];
echo(min(alldist));But your examples also gets at the question of what allowed
definitions of points are, the "random" points. Your definitions both
have to do with optimization, which means you've gone up a leap in
complexity from simple geometry. Points derived from optimization
aren't going to be clickable on a model. You can't "see" them. The
only way you can find these points is by doing the math.I can't run your model because it's full of parameters. But I would
think that in that case, at least, it would be possible to define your
model in terms of the width. If you start from the width and build
everything from there then you'll have the right width. That's the
kind of thing I meant when I wondered about the need for access to
distance values. The notion that you need to know the width of your
model after the fact so you can fix your botched model by trial and
error to make it the right width....doesn't appeal to me as a design
strategy. But if you really want to pursue trial-and-error design
then having a way to measure does seem very important. (It's unclear
to me if starting from the width just shifts the measurement problem
somewhere else, but it seems like if you have measurable parameters
you should be able to measure them and then design to the measurements
directly.)On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown
<openscad@jordan.maileater.net mailto:openscad@jordan.maileater.net>
wrote:On 8/29/2021 5:57 PM, Adrian Mariano wrote:The question I have is: why do you need to know where a point is? What are you trying to do that requires this knowledge in a real model? I wonder if there might be alternative approaches that don't require that information, or where the model can be structured so that it's easy to know where the point is. I suspect that at least some of the time, such alternative approaches may exist.I think the problem with straight "calculation" schemes is that they can get very hard, very fast. Quick, what's the distance between the closest points in these squares? rotate(a) square(10); translate([20,20]) rotate(b) square(10); You're a much stronger math guy than I am, so maybe you can do that off the top of your head, but it would take me some pretty serious thinking. And that's a simple case. In a real project... as I've mentioned, a lot of my work is in scale models. I was designing an armchair: https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg Here's what generates the sides and arms: // Sides for (s=[-1, 1]) { translate([s*w/2, d, leg_h+seat_h]) { rotate([90, 0, -90]) clip(v=[0,0,s]) { pipe_polygon(r=wing_t, fill=true, open=true, [ [3*inch, 0], [18*inch, 0], [18*inch, 8.5*inch], [4*inch, 8.5*inch], [3.5*inch, 17*inch], [4*inch, 26*inch], [-3.8*inch, 28*inch] ]); } // Arms translate([s*0*inch, -20.75*inch, 8.75*inch]) rotate([-86.5,0,4*s]) cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch); } } All of those dimensions are measured by hand off the real object, and the angles are eyeballed. Now, what's the width, measured between the outsides of the two arms? I want to tweak the angles and sizes so that's it's pretty close to correct.
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
... but now I do!
https://www.dropbox.com/s/sbual4uau6mjetq/RayCone2.jpg?raw=1
My email reader (Agent) displayed your message like this, and I pasted
without reading properly.
This is a multi-part message in MIME format.
--===============8943534100889042687==
Content-Type: multipart/alternative;
boundary="------------77B433390DBBD069FF37BF6E"
Content-Language: en-GB
This is a multi-part message in MIME format.
--------------77B433390DBBD069FF37BF6E
Content-Type: text/plain; charset=utf-8; format=flowed
Content-Transfer-Encoding: quoted-printable
Going back to my original bit of code with the two cones, I would
like=20
to be able to calculate the xyz coordinates of this cone tip. (it
being=20
60 years since 'I did O-level Maths', and I can't get my head around
this=
)
rotate([80,40,20])cylinder(h=3D10, d1=3D10, d2=3D0);
Thanks.
No idea why; I'll investigate.
P.S. My maths is if similar vintage.
Terry
====================
On Tue, 31 Aug 2021 13:42:25 +0100, you wrote:
Going back to my original bit of code with the two cones, I would like
to be able to calculate the xyz coordinates of this cone tip. (it being
60 years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are
fond of doing everything from first principles every time, which makes
them more painful than might be necessary. But my quick solution to
your squares problem:sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1),
select(sq2,j,j+1))];
echo(min(alldist));But your examples also gets at the question of what allowed
definitions of points are, the "random" points. Your definitions both
have to do with optimization, which means you've gone up a leap in
complexity from simple geometry. Points derived from optimization
aren't going to be clickable on a model. You can't "see" them. The
only way you can find these points is by doing the math.I can't run your model because it's full of parameters. But I would
think that in that case, at least, it would be possible to define your
model in terms of the width. If you start from the width and build
everything from there then you'll have the right width. That's the
kind of thing I meant when I wondered about the need for access to
distance values. The notion that you need to know the width of your
model after the fact so you can fix your botched model by trial and
error to make it the right width....doesn't appeal to me as a design
strategy. But if you really want to pursue trial-and-error design
then having a way to measure does seem very important. (It's unclear
to me if starting from the width just shifts the measurement problem
somewhere else, but it seems like if you have measurable parameters
you should be able to measure them and then design to the measurements
directly.)On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown
<openscad@jordan.maileater.net mailto:openscad@jordan.maileater.net>
wrote:On 8/29/2021 5:57 PM, Adrian Mariano wrote:The question I have is: why do you need to know where a point is? What are you trying to do that requires this knowledge in a real model? I wonder if there might be alternative approaches that don't require that information, or where the model can be structured so that it's easy to know where the point is. I suspect that at least some of the time, such alternative approaches may exist.I think the problem with straight "calculation" schemes is that they can get very hard, very fast. Quick, what's the distance between the closest points in these squares? rotate(a) square(10); translate([20,20]) rotate(b) square(10); You're a much stronger math guy than I am, so maybe you can do that off the top of your head, but it would take me some pretty serious thinking. And that's a simple case. In a real project... as I've mentioned, a lot of my work is in scale models. I was designing an armchair: https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg Here's what generates the sides and arms: // Sides for (s=[-1, 1]) { translate([s*w/2, d, leg_h+seat_h]) { rotate([90, 0, -90]) clip(v=[0,0,s]) { pipe_polygon(r=wing_t, fill=true, open=true, [ [3*inch, 0], [18*inch, 0], [18*inch, 8.5*inch], [4*inch, 8.5*inch], [3.5*inch, 17*inch], [4*inch, 26*inch], [-3.8*inch, 28*inch] ]); } // Arms translate([s*0*inch, -20.75*inch, 8.75*inch]) rotate([-86.5,0,4*s]) cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch); } } All of those dimensions are measured by hand off the real object, and the angles are eyeballed. Now, what's the width, measured between the outsides of the two arms? I want to tweak the angles and sizes so that's it's pretty close to correct.
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
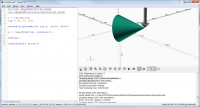
Try this:
include <NopSCADlib/lib.scad>
use <NopSCADlib/utils/annotation.scad>
r = [80,40,20];
tip = [0, 0, 10];
rotate(r)cylinder(h= tip.z, d1=10, d2=0);
p = transform(tip, rotate(r));
echo(p);
translate(p) arrow();
[image: image.png]
On Tue, 31 Aug 2021 at 14:01, Terry terrypingm@gmail.com wrote:
... but now I do!
https://www.dropbox.com/s/sbual4uau6mjetq/RayCone2.jpg?raw=1
My email reader (Agent) displayed your message like this, and I pasted
without reading properly.
This is a multi-part message in MIME format.
--===============8943534100889042687==
Content-Type: multipart/alternative;
boundary="------------77B433390DBBD069FF37BF6E"
Content-Language: en-GB
This is a multi-part message in MIME format.
--------------77B433390DBBD069FF37BF6E
Content-Type: text/plain; charset=utf-8; format=flowed
Content-Transfer-Encoding: quoted-printable
Going back to my original bit of code with the two cones, I would
like=20
to be able to calculate the xyz coordinates of this cone tip. (it
being=20
60 years since 'I did O-level Maths', and I can't get my head around
this=
)
rotate([80,40,20])cylinder(h=3D10, d1=3D10, d2=3D0);
Thanks.
No idea why; I'll investigate.
P.S. My maths is if similar vintage.
Terry
====================
On Tue, 31 Aug 2021 13:42:25 +0100, you wrote:
Going back to my original bit of code with the two cones, I would like
to be able to calculate the xyz coordinates of this cone tip. (it being
60 years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are
fond of doing everything from first principles every time, which makes
them more painful than might be necessary. But my quick solution to
your squares problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1),
select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed
definitions of points are, the "random" points. Your definitions both
have to do with optimization, which means you've gone up a leap in
complexity from simple geometry. Points derived from optimization
aren't going to be clickable on a model. You can't "see" them. The
only way you can find these points is by doing the math.
I can't run your model because it's full of parameters. But I would
think that in that case, at least, it would be possible to define your
model in terms of the width. If you start from the width and build
everything from there then you'll have the right width. That's the
kind of thing I meant when I wondered about the need for access to
distance values. The notion that you need to know the width of your
model after the fact so you can fix your botched model by trial and
error to make it the right width....doesn't appeal to me as a design
strategy. But if you really want to pursue trial-and-error design
then having a way to measure does seem very important. (It's unclear
to me if starting from the width just shifts the measurement problem
somewhere else, but it seems like if you have measurable parameters
you should be able to measure them and then design to the measurements
directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown
<openscad@jordan.maileater.net mailto:openscad@jordan.maileater.net>
wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a point
is? What are you trying to do that requires this knowledge in a
real model? I wonder if there might be alternative approaches
that don't require that information, or where the model can be
structured so that it's easy to know where the point is. I
suspect that at least some of the time, such alternative
approaches may exist.
I think the problem with straight "calculation" schemes is that
they can get very hard, very fast.
Quick, what's the distance between the closest points in these
squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can do
that off the top of your head, but it would take me some pretty
serious thinking. And that's a simple case.
In a real project... as I've mentioned, a lot of my work is in
scale models. I was designing an armchair:
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true,
open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2,
h=16*inch);
}
}
All of those dimensions are measured by hand off the real object,
and the angles are eyeballed.
Now, what's the width, measured between the outsides of the two
arms? I want to tweak the angles and sizes so that's it's pretty
close to correct.
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I see that nophead has given one solution to the problem of finding the tip
of this cone:
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
It's also easy to do with BOSL2. (I note I neglected to include the
"include<BOSL2/std.scad>" in my previous example.)
include<BOSL2/std.scad>
echo(rot([80,40,20], p=[0,0,10]));
If you want to know how this is actually working, basically you construct
the same rotation matrix that rotate() is using and apply it to the cone
tip. If you want to do stuff like this then in my opinion you should do it
once and put it in a library. (Or do it zero times yourself and use
nopscadlib or BOSL2, or dotSCAD.) There is a certain amount of
"reinventing OpenSCAD" in that doing this requires writing code that does
the same thing that rotate() does. There was vague talk of a proposal to
expose object geometry to users using the new function literals. I don't
know if it's something likely to happen someday. But even if it did, you
still have the problem of: given a cone as a list of points and faces, how
do you find the vertex?
But again I wonder about the use case for this. Personally I never invoke
rotate with more than one angle---do you actually use vector angles like
this? Why do you want to know where the tip of the cone is at that weird
angle? If it's because you want to put an object there then you don't
need to know where the point is. You just need to be able to make an
object go there. That's a different requirement. That's why I'm wondering
about what the real use case is. In the case of Jordan's models he wants
to design by trial and error and in that case there's no way around needing
to measure your model so that you can determine what the error is. But I
remain curious about other situations where you need to know where
something is that are not artificial, because I wonder if there's a
different way to solve them. In my own modeling I usually want to
position things in relation to other things, and this does NOT require that
I actually know the coordinates of any of the objects in my model. The
case that's problematic is if you want to create an object in relation to
TWO (or more) other things, but I have not encountered that case in my own
modeling. That is, if something needs to be sized based on 2 things
there's really some other fundamental size underlying it all. So I don't
understand a practical situation where you need the distance between the
tips of two arbitrarily rotated cones.
On Tue, Aug 31, 2021 at 8:42 AM Ray West raywest@raywest.com wrote:
Going back to my original bit of code with the two cones, I would like to
be able to calculate the xyz coordinates of this cone tip. (it being 60
years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are fond
of doing everything from first principles every time, which makes them more
painful than might be necessary. But my quick solution to your squares
problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1),
select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed definitions of
points are, the "random" points. Your definitions both have to do with
optimization, which means you've gone up a leap in complexity from simple
geometry. Points derived from optimization aren't going to be clickable on
a model. You can't "see" them. The only way you can find these points
is by doing the math.
I can't run your model because it's full of parameters. But I would think
that in that case, at least, it would be possible to define your model in
terms of the width. If you start from the width and build everything from
there then you'll have the right width. That's the kind of thing I meant
when I wondered about the need for access to distance values. The notion
that you need to know the width of your model after the fact so you can fix
your botched model by trial and error to make it the right width....doesn't
appeal to me as a design strategy. But if you really want to pursue
trial-and-error design then having a way to measure does seem very
important. (It's unclear to me if starting from the width just shifts the
measurement problem somewhere else, but it seems like if you have
measurable parameters you should be able to measure them and then design to
the measurements directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown <
openscad@jordan.maileater.net> wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a point is? What
are you trying to do that requires this knowledge in a real model? I
wonder if there might be alternative approaches that don't require that
information, or where the model can be structured so that it's easy to know
where the point is. I suspect that at least some of the time, such
alternative approaches may exist.
I think the problem with straight "calculation" schemes is that they can
get very hard, very fast.
Quick, what's the distance between the closest points in these squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can do that off
the top of your head, but it would take me some pretty serious thinking.
And that's a simple case.
In a real project... as I've mentioned, a lot of my work is in scale
models. I was designing an armchair:
[image:
https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg]
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true, open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch);
}
}
All of those dimensions are measured by hand off the real object, and the
angles are eyeballed.
Now, what's the width, measured between the outsides of the two arms? I
want to tweak the angles and sizes so that's it's pretty close to correct.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
The idea was to generate a couple of points, that i would not have any
precise idea where they were, for what I originally thought was a test
for the measuring tool that i mistakenly thought was being talked about
earlier. Now, I have gone back to thinking that If I calculate the
positions, then I can check my eyeballing technique errors, just a test.
I am also thinking, in the back of my mind, of the possibility of using
the openscad scad text file as the input to some other program, to see
if distance can be calculated there. I've a thought that it could be
possible for designs made of simple shapes, but the maths would be
beyond me for anything complicated. From what I've seen, for rotating
points, as per cone, it involves matrix calculations, which if I ever
learnt anything about them, now, I've completely forgotten.
Best wishes,
Ray
On 31/08/2021 19:42, Adrian Mariano wrote:
I see that nophead has given one solution to the problem of finding
the tip of this cone:
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
It's also easy to do with BOSL2. (I note I neglected to include the
"include<BOSL2/std.scad>" in my previous example.)
include<BOSL2/std.scad>
echo(rot([80,40,20], p=[0,0,10]));
If you want to know how this is actually working, basically you
construct the same rotation matrix that rotate() is using and apply it
to the cone tip. If you want to do stuff like this then in my opinion
you should do it once and put it in a library. (Or do it zero times
yourself and use nopscadlib or BOSL2, or dotSCAD.) There is a certain
amount of "reinventing OpenSCAD" in that doing this requires writing
code that does the same thing that rotate() does. There was vague
talk of a proposal to expose object geometry to users using the new
function literals. I don't know if it's something likely to happen
someday. But even if it did, you still have the problem of: given a
cone as a list of points and faces, how do you find the vertex?
But again I wonder about the use case for this. Personally I never
invoke rotate with more than one angle---do you actually use vector
angles like this? Why do you want to know where the tip of the cone
is at that weird angle? If it's because you want to put an object
there then you don't need to know where the point is. You just need
to be able to make an object go there. That's a different
requirement. That's why I'm wondering about what the real use case
is. In the case of Jordan's models he wants to design by trial and
error and in that case there's no way around needing to measure your
model so that you can determine what the error is. But I remain
curious about other situations where you need to know where something
is that are not artificial, because I wonder if there's a different
way to solve them. In my own modeling I usually want to position
things in relation to other things, and this does NOT require that I
actually know the coordinates of any of the objects in my model. The
case that's problematic is if you want to create an object in relation
to TWO (or more) other things, but I have not encountered that case in
my own modeling. That is, if something needs to be sized based on 2
things there's really some other fundamental size underlying it all.
So I don't understand a practical situation where you need the
distance between the tips of two arbitrarily rotated cones.
On Tue, Aug 31, 2021 at 8:42 AM Ray West <raywest@raywest.com
mailto:raywest@raywest.com> wrote:
Going back to my original bit of code with the two cones, I would
like to be able to calculate the xyz coordinates of this cone tip.
(it being 60 years since 'I did O-level Maths', and I can't get my
head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here
are fond of doing everything from first principles every time,
which makes them more painful than might be necessary. But my
quick solution to your squares problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3])
segment_distance(select(sq1,i,i+1), select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed
definitions of points are, the "random" points. Your definitions
both have to do with optimization, which means you've gone up a
leap in complexity from simple geometry. Points derived from
optimization aren't going to be clickable on a model. You can't
"see" them. The *only* way you can find these points is by doing
the math.
I can't run your model because it's full of parameters. But I
would think that in that case, at least, it would be possible to
define your model in terms of the width. If you start from the
width and build everything from there then you'll have the right
width. That's the kind of thing I meant when I wondered about
the need for access to distance values. The notion that you need
to know the width of your model after the fact so you can fix
your botched model by trial and error to make it the right
width....doesn't appeal to me as a design strategy. But if you
really want to pursue trial-and-error design then having a way to
measure does seem very important. (It's unclear to me if
starting from the width just shifts the measurement problem
somewhere else, but it seems like if you have measurable
parameters you should be able to measure them and then design to
the measurements directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown
<openscad@jordan.maileater.net
<mailto:openscad@jordan.maileater.net>> wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a
point is? What are you trying to do that requires this
knowledge in a real model? I wonder if there might be
alternative approaches that don't require that information,
or where the model can be structured so that it's easy to
know where the point is. I suspect that at least some of
the time, such alternative approaches may exist.
I think the problem with straight "calculation" schemes is
that they can get very hard, very fast.
Quick, what's the distance between the closest points in
these squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can
do that off the top of your head, but it would take me some
pretty serious thinking. And that's a simple case.
In a real project... as I've mentioned, a lot of my work is
in scale models. I was designing an armchair:
https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true, open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch);
}
}
All of those dimensions are measured by hand off the real
object, and the angles are eyeballed.
Now, what's the width, measured between the outsides of the
two arms? I want to tweak the angles and sizes so that's
it's pretty close to correct.
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org <mailto:discuss-leave@lists.openscad.org>
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
<mailto:discuss-leave@lists.openscad.org>
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
There is of course the case of points on import() or surface().
From: Adrian Mariano [mailto:avm4@cornell.edu]
Sent: Wed, 1 Sep 2021 04:42
To: OpenSCAD general discussion
Subject: [OpenSCAD] Re: Provide a simple measurement tool
I see that nophead has given one solution to the problem of finding the tip of this cone:
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
It's also easy to do with BOSL2. (I note I neglected to include the "include<BOSL2/std.scad>" in my previous example.)
include<BOSL2/std.scad>
echo(rot([80,40,20], p=[0,0,10]));
If you want to know how this is actually working, basically you construct the same rotation matrix that rotate() is using and apply it to the cone tip. If you want to do stuff like this then in my opinion you should do it once and put it in a library. (Or do it zero times yourself and use nopscadlib or BOSL2, or dotSCAD.) There is a certain amount of "reinventing OpenSCAD" in that doing this requires writing code that does the same thing that rotate() does. There was vague talk of a proposal to expose object geometry to users using the new function literals. I don't know if it's something likely to happen someday. But even if it did, you still have the problem of: given a cone as a list of points and faces, how do you find the vertex?
But again I wonder about the use case for this. Personally I never invoke rotate with more than one angle---do you actually use vector angles like this? Why do you want to know where the tip of the cone is at that weird angle? If it's because you want to put an object there then you don't need to know where the point is. You just need to be able to make an object go there. That's a different requirement. That's why I'm wondering about what the real use case is. In the case of Jordan's models he wants to design by trial and error and in that case there's no way around needing to measure your model so that you can determine what the error is. But I remain curious about other situations where you need to know where something is that are not artificial, because I wonder if there's a different way to solve them. In my own modeling I usually want to position things in relation to other things, and this does NOT require that I actually know the coordinates of any of the objects in my model. The case that's problematic is if you want to create an object in relation to TWO (or more) other things, but I have not encountered that case in my own modeling. That is, if something needs to be sized based on 2 things there's really some other fundamental size underlying it all. So I don't understand a practical situation where you need the distance between the tips of two arbitrarily rotated cones.
On Tue, Aug 31, 2021 at 8:42 AM Ray West raywest@raywest.com wrote:
Going back to my original bit of code with the two cones, I would like to be able to calculate the xyz coordinates of this cone tip. (it being 60 years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are fond of doing everything from first principles every time, which makes them more painful than might be necessary. But my quick solution to your squares problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1), select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed definitions of points are, the "random" points. Your definitions both have to do with optimization, which means you've gone up a leap in complexity from simple geometry. Points derived from optimization aren't going to be clickable on a model. You can't "see" them. The only way you can find these points is by doing the math.
I can't run your model because it's full of parameters. But I would think that in that case, at least, it would be possible to define your model in terms of the width. If you start from the width and build everything from there then you'll have the right width. That's the kind of thing I meant when I wondered about the need for access to distance values. The notion that you need to know the width of your model after the fact so you can fix your botched model by trial and error to make it the right width....doesn't appeal to me as a design strategy. But if you really want to pursue trial-and-error design then having a way to measure does seem very important. (It's unclear to me if starting from the width just shifts the measurement problem somewhere else, but it seems like if you have measurable parameters you should be able to measure them and then design to the measurements directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown openscad@jordan.maileater.net wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a point is? What are you trying to do that requires this knowledge in a real model? I wonder if there might be alternative approaches that don't require that information, or where the model can be structured so that it's easy to know where the point is. I suspect that at least some of the time, such alternative approaches may exist.
I think the problem with straight "calculation" schemes is that they can get very hard, very fast.
Quick, what's the distance between the closest points in these squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can do that off the top of your head, but it would take me some pretty serious thinking. And that's a simple case.
In a real project... as I've mentioned, a lot of my work is in scale models. I was designing an armchair:
https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true, open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch);
}
}
All of those dimensions are measured by hand off the real object, and the angles are eyeballed.
Now, what's the width, measured between the outsides of the two arms? I want to tweak the angles and sizes so that's it's pretty close to correct.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
--
This email has been checked for viruses by AVG.
https://www.avg.com
I've simplified my eyeballing technique, distances can be measured
fairly quickly.
I start off by defining the tolerance I'm happy with.
I've made a module named tol() and set it to 0.5 for this example
module tol(t){
# sphere(t);
}
then I place a tolerance sphere at each of the two points I'm measuring
between
e.g. like
p1=([0,0,10]);
translate(p1)tol(); // first point
p2=([54.5,11.2,41.3]);
translate(p2)tol(); // second point
They are easy to position, one at a time, by positioning x,y from the
top or bottom view, adjusting the appropriate values in PI or P2, and
then position z from one of the other views. zooming or rotating the
view as required.
then the distance can be echoed by something like
module dist(p1,p2){
dx= p2.x-p1.x;
dy= p2.y-p1.y;
dz= p2.z-p2.y;
l= sqrt((dxdx) +(dydy) +(dz*dz));
echo(distance = l);
}
provided the points of interest lie within the tolerance spheres, I get
the distance between the points within my defined tolerance,. If I want
a more accurate result, I can reduce the tolerance and zoom in closer
when positioning the spheres. If the tolerance sphere is too small, to
see on the full size view, then I could easily place a few rings around
them, or similar.
On 31/08/2021 22:31, Ray West wrote:
The idea was to generate a couple of points, that i would not have any
precise idea where they were, for what I originally thought was a test
for the measuring tool that i mistakenly thought was being talked
about earlier. Now, I have gone back to thinking that If I calculate
the positions, then I can check my eyeballing technique errors, just a
test. I am also thinking, in the back of my mind, of the possibility
of using the openscad scad text file as the input to some other
program, to see if distance can be calculated there. I've a thought
that it could be possible for designs made of simple shapes, but the
maths would be beyond me for anything complicated. From what I've
seen, for rotating points, as per cone, it involves matrix
calculations, which if I ever learnt anything about them, now, I've
completely forgotten.
Best wishes,
Ray
On 31/08/2021 19:42, Adrian Mariano wrote:
I see that nophead has given one solution to the problem of finding
the tip of this cone:
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
It's also easy to do with BOSL2. (I note I neglected to include the
"include<BOSL2/std.scad>" in my previous example.)
include<BOSL2/std.scad>
echo(rot([80,40,20], p=[0,0,10]));
If you want to know how this is actually working, basically you
construct the same rotation matrix that rotate() is using and apply
it to the cone tip. If you want to do stuff like this then in my
opinion you should do it once and put it in a library. (Or do it
zero times yourself and use nopscadlib or BOSL2, or dotSCAD.) There
is a certain amount of "reinventing OpenSCAD" in that doing this
requires writing code that does the same thing that rotate() does.
There was vague talk of a proposal to expose object geometry to users
using the new function literals. I don't know if it's something
likely to happen someday. But even if it did, you still have the
problem of: given a cone as a list of points and faces, how do you
find the vertex?
But again I wonder about the use case for this. Personally I never
invoke rotate with more than one angle---do you actually use vector
angles like this? Why do you want to know where the tip of the cone
is at that weird angle? If it's because you want to put an object
there then you don't need to know where the point is. You just need
to be able to make an object go there. That's a different
requirement. That's why I'm wondering about what the real use case
is. In the case of Jordan's models he wants to design by trial and
error and in that case there's no way around needing to measure your
model so that you can determine what the error is. But I remain
curious about other situations where you need to know where something
is that are not artificial, because I wonder if there's a different
way to solve them. In my own modeling I usually want to position
things in relation to other things, and this does NOT require that I
actually know the coordinates of any of the objects in my model. The
case that's problematic is if you want to create an object in
relation to TWO (or more) other things, but I have not encountered
that case in my own modeling. That is, if something needs to be
sized based on 2 things there's really some other fundamental size
underlying it all. So I don't understand a practical situation where
you need the distance between the tips of two arbitrarily rotated cones.
On Tue, Aug 31, 2021 at 8:42 AM Ray West <raywest@raywest.com
mailto:raywest@raywest.com> wrote:
Going back to my original bit of code with the two cones, I would
like to be able to calculate the xyz coordinates of this cone
tip. (it being 60 years since 'I did O-level Maths', and I can't
get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here
are fond of doing everything from first principles every time,
which makes them more painful than might be necessary. But my
quick solution to your squares problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3])
segment_distance(select(sq1,i,i+1), select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed
definitions of points are, the "random" points. Your
definitions both have to do with optimization, which means
you've gone up a leap in complexity from simple geometry.
Points derived from optimization aren't going to be clickable on
a model. You can't "see" them. The *only* way you can find
these points is by doing the math.
I can't run your model because it's full of parameters. But I
would think that in that case, at least, it would be possible to
define your model in terms of the width. If you start from the
width and build everything from there then you'll have the right
width. That's the kind of thing I meant when I wondered about
the need for access to distance values. The notion that you
need to know the width of your model after the fact so you can
fix your botched model by trial and error to make it the right
width....doesn't appeal to me as a design strategy. But if you
really want to pursue trial-and-error design then having a way
to measure does seem very important. (It's unclear to me if
starting from the width just shifts the measurement problem
somewhere else, but it seems like if you have measurable
parameters you should be able to measure them and then design to
the measurements directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown
<openscad@jordan.maileater.net
<mailto:openscad@jordan.maileater.net>> wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a
point is? What are you trying to do that requires this
knowledge in a real model? I wonder if there might be
alternative approaches that don't require that information,
or where the model can be structured so that it's easy to
know where the point is. I suspect that at least some of
the time, such alternative approaches may exist.
I think the problem with straight "calculation" schemes is
that they can get very hard, very fast.
Quick, what's the distance between the closest points in
these squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can
do that off the top of your head, but it would take me some
pretty serious thinking. And that's a simple case.
In a real project... as I've mentioned, a lot of my work is
in scale models. I was designing an armchair:
https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true, open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch);
}
}
All of those dimensions are measured by hand off the real
object, and the angles are eyeballed.
Now, what's the width, measured between the outsides of the
two arms? I want to tweak the angles and sizes so that's
it's pretty close to correct.
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org <mailto:discuss-leave@lists.openscad.org>
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
<mailto:discuss-leave@lists.openscad.org>
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
A reminder, in the editor put the cursor next to a number and Alt-Up/Down changes it and previews, handy for such adjustments.
And/or you could restructure it to use customizer to move them around??
From: Ray West [mailto:raywest@raywest.com]
Sent: Thu, 2 Sep 2021 08:57
To: discuss@lists.openscad.org
Subject: [OpenSCAD] Re: Provide a simple measurement tool
I've simplified my eyeballing technique, distances can be measured fairly quickly.
I start off by defining the tolerance I'm happy with.
I've made a module named tol() and set it to 0.5 for this example
module tol(t){
# sphere(t);
}
then I place a tolerance sphere at each of the two points I'm measuring between
e.g. like
p1=([0,0,10]);
translate(p1)tol(); // first point
p2=([54.5,11.2,41.3]);
translate(p2)tol(); // second point
They are easy to position, one at a time, by positioning x,y from the top or bottom view, adjusting the appropriate values in PI or P2, and then position z from one of the other views. zooming or rotating the view as required.
then the distance can be echoed by something like
module dist(p1,p2){
dx= p2.x-p1.x;
dy= p2.y-p1.y;
dz= p2.z-p2.y;
l= sqrt((dxdx) +(dydy) +(dz*dz));
echo(distance = l);
}
provided the points of interest lie within the tolerance spheres, I get the distance between the points within my defined tolerance,. If I want a more accurate result, I can reduce the tolerance and zoom in closer when positioning the spheres. If the tolerance sphere is too small, to see on the full size view, then I could easily place a few rings around them, or similar.
On 31/08/2021 22:31, Ray West wrote:
The idea was to generate a couple of points, that i would not have any precise idea where they were, for what I originally thought was a test for the measuring tool that i mistakenly thought was being talked about earlier. Now, I have gone back to thinking that If I calculate the positions, then I can check my eyeballing technique errors, just a test. I am also thinking, in the back of my mind, of the possibility of using the openscad scad text file as the input to some other program, to see if distance can be calculated there. I've a thought that it could be possible for designs made of simple shapes, but the maths would be beyond me for anything complicated. From what I've seen, for rotating points, as per cone, it involves matrix calculations, which if I ever learnt anything about them, now, I've completely forgotten.
Best wishes,
Ray
On 31/08/2021 19:42, Adrian Mariano wrote:
I see that nophead has given one solution to the problem of finding the tip of this cone:
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
It's also easy to do with BOSL2. (I note I neglected to include the "include<BOSL2/std.scad>" in my previous example.)
include<BOSL2/std.scad>
echo(rot([80,40,20], p=[0,0,10]));
If you want to know how this is actually working, basically you construct the same rotation matrix that rotate() is using and apply it to the cone tip. If you want to do stuff like this then in my opinion you should do it once and put it in a library. (Or do it zero times yourself and use nopscadlib or BOSL2, or dotSCAD.) There is a certain amount of "reinventing OpenSCAD" in that doing this requires writing code that does the same thing that rotate() does. There was vague talk of a proposal to expose object geometry to users using the new function literals. I don't know if it's something likely to happen someday. But even if it did, you still have the problem of: given a cone as a list of points and faces, how do you find the vertex?
But again I wonder about the use case for this. Personally I never invoke rotate with more than one angle---do you actually use vector angles like this? Why do you want to know where the tip of the cone is at that weird angle? If it's because you want to put an object there then you don't need to know where the point is. You just need to be able to make an object go there. That's a different requirement. That's why I'm wondering about what the real use case is. In the case of Jordan's models he wants to design by trial and error and in that case there's no way around needing to measure your model so that you can determine what the error is. But I remain curious about other situations where you need to know where something is that are not artificial, because I wonder if there's a different way to solve them. In my own modeling I usually want to position things in relation to other things, and this does NOT require that I actually know the coordinates of any of the objects in my model. The case that's problematic is if you want to create an object in relation to TWO (or more) other things, but I have not encountered that case in my own modeling. That is, if something needs to be sized based on 2 things there's really some other fundamental size underlying it all. So I don't understand a practical situation where you need the distance between the tips of two arbitrarily rotated cones.
On Tue, Aug 31, 2021 at 8:42 AM Ray West raywest@raywest.com wrote:
Going back to my original bit of code with the two cones, I would like to be able to calculate the xyz coordinates of this cone tip. (it being 60 years since 'I did O-level Maths', and I can't get my head around this)
rotate([80,40,20])cylinder(h=10, d1=10, d2=0);
Thanks.
On 30/08/2021 20:43, Adrian Mariano wrote:
Yes, geometrical calculations can be painful. I know people here are fond of doing everything from first principles every time, which makes them more painful than might be necessary. But my quick solution to your squares problem:
sq1 = rot(a,p=square(10));
sq2 = right(20,p=rot(b,p=square(10)));
stroke(sq1,closed=true);
stroke(sq2,closed=true);
alldist = [for(i=[0:3], j=[0:3]) segment_distance(select(sq1,i,i+1), select(sq2,j,j+1))];
echo(min(alldist));
But your examples also gets at the question of what allowed definitions of points are, the "random" points. Your definitions both have to do with optimization, which means you've gone up a leap in complexity from simple geometry. Points derived from optimization aren't going to be clickable on a model. You can't "see" them. The only way you can find these points is by doing the math.
I can't run your model because it's full of parameters. But I would think that in that case, at least, it would be possible to define your model in terms of the width. If you start from the width and build everything from there then you'll have the right width. That's the kind of thing I meant when I wondered about the need for access to distance values. The notion that you need to know the width of your model after the fact so you can fix your botched model by trial and error to make it the right width....doesn't appeal to me as a design strategy. But if you really want to pursue trial-and-error design then having a way to measure does seem very important. (It's unclear to me if starting from the width just shifts the measurement problem somewhere else, but it seems like if you have measurable parameters you should be able to measure them and then design to the measurements directly.)
On Mon, Aug 30, 2021 at 12:45 PM Jordan Brown openscad@jordan.maileater.net wrote:
On 8/29/2021 5:57 PM, Adrian Mariano wrote:
The question I have is: why do you need to know where a point is? What are you trying to do that requires this knowledge in a real model? I wonder if there might be alternative approaches that don't require that information, or where the model can be structured so that it's easy to know where the point is. I suspect that at least some of the time, such alternative approaches may exist.
I think the problem with straight "calculation" schemes is that they can get very hard, very fast.
Quick, what's the distance between the closest points in these squares?
rotate(a) square(10);
translate([20,20]) rotate(b) square(10);
You're a much stronger math guy than I am, so maybe you can do that off the top of your head, but it would take me some pretty serious thinking. And that's a simple case.
In a real project... as I've mentioned, a lot of my work is in scale models. I was designing an armchair:
https://cdn.thingiverse.com/assets/ed/00/42/d1/65/featured_preview_WIN_20200407_22_06_02_Pro.jpg
Here's what generates the sides and arms:
// Sides
for (s=[-1, 1]) {
translate([s*w/2, d, leg_h+seat_h]) {
rotate([90, 0, -90])
clip(v=[0,0,s]) {
pipe_polygon(r=wing_t, fill=true, open=true, [
[3*inch, 0],
[18*inch, 0],
[18*inch, 8.5*inch],
[4*inch, 8.5*inch],
[3.5*inch, 17*inch],
[4*inch, 26*inch],
[-3.8*inch, 28*inch]
]);
}
// Arms
translate([s*0*inch, -20.75*inch, 8.75*inch])
rotate([-86.5,0,4*s])
cylinder(d2=wing_t*1.3, d1=wing_t*2, h=16*inch);
}
}
All of those dimensions are measured by hand off the real object, and the angles are eyeballed.
Now, what's the width, measured between the outsides of the two arms? I want to tweak the angles and sizes so that's it's pretty close to correct.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
--
This email has been checked for viruses by AVG.
https://www.avg.com
On 02/09/2021 00:11, MichaelAtOz wrote:
A reminder, in the editor put the cursor next to a number and
Alt-Up/Down changes it and previews, handy for such adjustments.
Thanks - handy for fine tuning, - I didn't know that (along with much of
this ;-),
I don't use the customizer, I tend to put the variables i want to change
at the top of script.