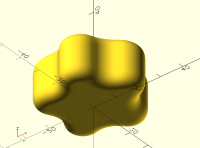
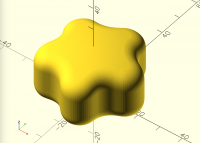
reduction of computing time - ideas?
This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
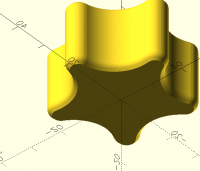
I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Another way would be to do the convex decomposition by yourself, I think it
can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems
with not closed mesh) but a different problem. Should I have asked in the
old thread anyway?
I create star shaped knobs for hex screws (see
https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
The rounded top surface is achieved by subtracting from a large sphere (see
prototype code below) and the rounded edges are created with the minkowski
sum. Since the sphere must be large for a low rounding it needs a large $fn
value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3
CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape
analytically instead of using unions and differences. This way I was able
to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time
even further? The reason: I create a web based configuration tool and would
like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of arm
and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
If the knob is to be 3d fdm printed by others, then the rounded edges
will look awful. Minkowski is slow, especially if $fn is large. I would
suggest a redesign of the knob. I posted on here, a few weeks ago (re:
bad children) some simple bevel modules. (They sliced at 0.1mm
intervals, but that and the profile could be varied). It gives much
faster results than using Minkowski. Basically, you could draw the
profile of the knob in 2d, linear extrude it to the desired thickness,
then apply the bevel/rounding modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I
think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path,
and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago
(problems with not closed mesh) but a different problem. Should I
have asked in the old thread anyway?
I create star shaped knobs for hex screws (see
https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
The rounded top surface is achieved by subtracting from a large
sphere (see prototype code below) and the rounded edges are
created with the minkowski sum. Since the sphere must be large for
a low rounding it needs a large $fn value (120 currently). Thus,
the minkowski sum needs about 80 seconds (M3 CPU) to generate the
object with manifold backend.
This is already an optimized version since I create the basic
star shape analytically instead of using unions and differences.
This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing
time even further? The reason: I create a web based configuration
tool and would like to provide the stl file in less than ten seconds.
/**
* prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch
point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
I'm not sure what Ray has against rounded edges. I use them all the time
and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual
dome top of the knob, which tends to have a very exposed layer line
step-structure with very wide and visible steps that I think look and feel
pretty bad. That will be worse the closer you are to flat---I don't know
how bad it would look with the model as shown. I printed a knob to go on
my audio amp and my first version had a domed top like shown and I
scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside
down. That needs to be a chamfer or teardrop for the best result. So I'd
probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2),
top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix, which
is the corners where the tip circles meet the notch circles. For a truly
beautiful knob the tangents should match so that you don't have corners
there.
Oh, and one other thing that will make this faster no matter how you
proceed is to stop using so many points. The smallest facet is 0.22 mm in
the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic
method. You'd need to form a grid over the top of the knob to form the
polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and bottom:
[image: image.png]
[image: image.png]
Avoiding the lower angle at the bottom by switching to a chamfer will
ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges will
look awful. Minkowski is slow, especially if $fn is large. I would suggest
a redesign of the knob. I posted on here, a few weeks ago (re: bad
children) some simple bevel modules. (They sliced at 0.1mm intervals, but
that and the profile could be varied). It gives much faster results than
using Minkowski. Basically, you could draw the profile of the knob in 2d,
linear extrude it to the desired thickness, then apply the bevel/rounding
modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I think
it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems
with not closed mesh) but a different problem. Should I have asked in the
old thread anyway?
I create star shaped knobs for hex screws (see
https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
The rounded top surface is achieved by subtracting from a large sphere (see
prototype code below) and the rounded edges are created with the minkowski
sum. Since the sphere must be large for a low rounding it needs a large $fn
value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3
CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star
shape analytically instead of using unions and differences. This way I was
able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time
even further? The reason: I create a web based configuration tool and would
like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of
arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Adaptive layer height in slicers is good for curved top surfaces.
[image: IMG_20231218_202013684.jpg]
On Thu, 26 Dec 2024 at 15:03, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
I'm not sure what Ray has against rounded edges. I use them all the time
and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual
dome top of the knob, which tends to have a very exposed layer line
step-structure with very wide and visible steps that I think look and feel
pretty bad. That will be worse the closer you are to flat---I don't know
how bad it would look with the model as shown. I printed a knob to go on
my audio amp and my first version had a domed top like shown and I
scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside
down. That needs to be a chamfer or teardrop for the best result. So I'd
probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2),
top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix, which
is the corners where the tip circles meet the notch circles. For a truly
beautiful knob the tangents should match so that you don't have corners
there.
Oh, and one other thing that will make this faster no matter how you
proceed is to stop using so many points. The smallest facet is 0.22 mm in
the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic
method. You'd need to form a grid over the top of the knob to form the
polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and
bottom:
[image: image.png]
[image: image.png]
Avoiding the lower angle at the bottom by switching to a chamfer will
ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges
will look awful. Minkowski is slow, especially if $fn is large. I would
suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad
children) some simple bevel modules. (They sliced at 0.1mm intervals, but
that and the profile could be varied). It gives much faster results than
using Minkowski. Basically, you could draw the profile of the knob in 2d,
linear extrude it to the desired thickness, then apply the bevel/rounding
modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I think
it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems
with not closed mesh) but a different problem. Should I have asked in the
old thread anyway?
I create star shaped knobs for hex screws (see
https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
The rounded top surface is achieved by subtracting from a large sphere (see
prototype code below) and the rounded edges are created with the minkowski
sum. Since the sphere must be large for a low rounding it needs a large $fn
value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3
CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star
shape analytically instead of using unions and differences. This way I was
able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time
even further? The reason: I create a web based configuration tool and would
like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of
arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Thank you for your insights. I get good results printing the rounded surface upside down and sanding it. You are right about the distance of the top layers, this tends to be visible the closer it gets to flat, but it's fine after sanding. Nonetheless, if you take a look at printables, there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds for brass castings.
The tangents of the tips and the notches actually match in both the version on printables (made with boolean operations) and the analytical version posted in this thread. The small edgy stripes between tips and notches are subject to low $fn values of the cylinders when creating the knob with boolean operations. With an analytically generated outline they don't appear at all. Could you please elaborate on the problems you experienced?
I make good progress creating the rounded top analytically. I generate a polyhedron from several layers of outlines with the radius changing with the cosine of the current step's angle. It is fast as hell, even with 360 steps around the edge it takes less than 50 milliseconds for two layers and I expect to be fine with about ten layers for the rounded edge. I can post the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this thread are strangely shaped faces at the rounded edge after doing the minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will also disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside down. That needs to be a chamfer or teardrop for the best result. So I'd probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix, which is the corners where the tip circles meet the notch circles. For a truly beautiful knob the tangents should match so that you don't have corners there.
Oh, and one other thing that will make this faster no matter how you proceed is to stop using so many points. The smallest facet is 0.22 mm in the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic method. You'd need to form a grid over the top of the knob to form the polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and bottom:
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss discuss@lists.openscad.org wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges will look awful. Minkowski is slow, especially if $fn is large. I would suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad children) some simple bevel modules. (They sliced at 0.1mm intervals, but that and the profile could be varied). It gives much faster results than using Minkowski. Basically, you could draw the profile of the knob in 2d, linear extrude it to the desired thickness, then apply the bevel/rounding modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Sanding well enough to produce a model that looks good is going to be a ton
of work---more work than I would put forth for a model. Casting is
obviously a different application, where appearance doesn't matter. But if
you're planning to offer a generator to people, I would guess most people
are in my camp: no interest in a bunch of post processing of the model. If
I had a project with 8 knobs it would loom even larger as a nuisance. What
would make sense for this is solvent smoothing...but I don't do that
either. (Not really feasible with PLA.)
Building structures analytically is generally very fast if you have a
reasonably straight forward analytic approach. I can't quite understand
your method to know what the result would look like---definitely post your
final result.
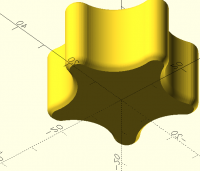
Regarding the corners, it's not super visible in the model as you gave it,
but when I changed armPitch to 3 I got this
[image: image.png]
The corner is very clear here. So if your math is producing a corner when
armPitch=3 then most likely there is exactly one value of armPitch (other
parameters held fixed) that generates a model where the tangents match and
there is no corner. I didn't try to understand your code enough to know
what's going on there. The corner is more subtle with less extreme
parameter choices, but may be tactile even if not obvious in the model on
screen.
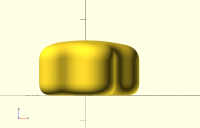
At armPitch of 3.2 there are now two obvious corners:
[image: image.png]
And these parameter values seem plausible use cases, not crazy outlier
values, so if you're providing a parameterized model it seems like they
should work.
On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss <
discuss@lists.openscad.org> wrote:
Thank you for your insights. I get good results printing the rounded
surface upside down and sanding it. You are right about the distance of
the top layers, this tends to be visible the closer it gets to flat, but
it's fine after sanding. Nonetheless, if you take a look at printables,
there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds for
brass castings.
The tangents of the tips and the notches actually match in both the
version on printables (made with boolean operations) and the analytical
version posted in this thread. The small edgy stripes between tips and
notches are subject to low $fn values of the cylinders when creating the
knob with boolean operations. With an analytically generated outline they
don't appear at all. Could you please elaborate on the problems you
experienced?
I make good progress creating the rounded top analytically. I generate a
polyhedron from several layers of outlines with the radius changing with
the cosine of the current step's angle. It is fast as hell, even with 360
steps around the edge it takes less than 50 milliseconds for two layers and
I expect to be fine with about ten layers for the rounded edge. I can post
the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this thread
are strangely shaped faces at the rounded edge after doing the minkowski.
The Prusa Slicer finds 20 errors in the resulting stl. This will also
disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss <
I'm not sure what Ray has against rounded edges. I use them all the
time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual
dome top of the knob, which tends to have a very exposed layer line
step-structure with very wide and visible steps that I think look and feel
pretty bad. That will be worse the closer you are to flat---I don't know
how bad it would look with the model as shown. I printed a knob to go on
my audio amp and my first version had a domed top like shown and I
scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside
down. That needs to be a chamfer or teardrop for the best result. So I'd
probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20,
bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix,
which is the corners where the tip circles meet the notch circles. For a
truly beautiful knob the tangents should match so that you don't have
corners there.
Oh, and one other thing that will make this faster no matter how you
proceed is to stop using so many points. The smallest facet is 0.22 mm in
the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic
method. You'd need to form a grid over the top of the knob to form the
polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and
bottom:
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will
ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges
will look awful. Minkowski is slow, especially if $fn is large. I would
suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad
children) some simple bevel modules. (They sliced at 0.1mm intervals, but
that and the profile could be varied). It gives much faster results than
using Minkowski. Basically, you could draw the profile of the knob in 2d,
linear extrude it to the desired thickness, then apply the bevel/rounding
modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I
think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com
wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems
with not closed mesh) but a different problem. Should I have asked in the
old thread anyway?
I create star shaped knobs for hex screws (see
https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
The rounded top surface is achieved by subtracting from a large sphere (see
prototype code below) and the rounded edges are created with the minkowski
sum. Since the sphere must be large for a low rounding it needs a large $fn
value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3
CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star
shape analytically instead of using unions and differences. This way I was
able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time
even further? The reason: I create a web based configuration tool and would
like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of
arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Manifold may produce self-intersections for some extreme cases, e.g.
when doing minkowski sum. This is tracked in
https://github.com/elalish/manifold/issues/970
On 12/27/24 00:25, Thomas Richter via Discuss wrote:
Thank you for your insights. I get good results printing the rounded surface upside down and sanding it. You are right about the distance of the top layers, this tends to be visible the closer it gets to flat, but it's fine after sanding. Nonetheless, if you take a look at printables, there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds for brass castings.
The tangents of the tips and the notches actually match in both the version on printables (made with boolean operations) and the analytical version posted in this thread. The small edgy stripes between tips and notches are subject to low $fn values of the cylinders when creating the knob with boolean operations. With an analytically generated outline they don't appear at all. Could you please elaborate on the problems you experienced?
I make good progress creating the rounded top analytically. I generate a polyhedron from several layers of outlines with the radius changing with the cosine of the current step's angle. It is fast as hell, even with 360 steps around the edge it takes less than 50 milliseconds for two layers and I expect to be fine with about ten layers for the rounded edge. I can post the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this thread are strangely shaped faces at the rounded edge after doing the minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will also disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside down. That needs to be a chamfer or teardrop for the best result. So I'd probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);to get that effect. There is another thing I'd probably try to fix, which is the corners where the tip circles meet the notch circles. For a truly beautiful knob the tangents should match so that you don't have corners there.
Oh, and one other thing that will make this faster no matter how you proceed is to stop using so many points. The smallest facet is 0.22 mm in the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic method. You'd need to form a grid over the top of the knob to form the polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and bottom:
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will ensure good printing.On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss discuss@lists.openscad.org wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges will look awful. Minkowski is slow, especially if $fn is large. I would suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad children) some simple bevel modules. (They sliced at 0.1mm intervals, but that and the profile could be varied). It gives much faster results than using Minkowski. Basically, you could draw the profile of the knob in 2d, linear extrude it to the desired thickness, then apply the bevel/rounding modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:Another way would be to do the convex decomposition by yourself, I think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));// radius of the knob's core: distance from center to touch point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)[rx * cos(phi), rx * sin(phi)]];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);difference() { translate([0, 0, -30]) sphere(d = 99, $fn = 120); difference () { translate([0, 0, -35]) cube(110, center = true); linear_extrude(20) polygon(points); } }}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Here is the python version:
from openscad2 import *
a=circle(30,s=6)
b=rot2d(360/5/2,circle(15,s=6))
star=c23(l_(concatenate(a_([a,b]).transpose(1,0,2))))
star=corner_radius(a_(star)+[0,0,7],20)
a1=rot('x90',arc_2p([-30,0],[30,0],70,s=50)[25:])
s1=translate([0,0,15],[rot(f'z{i}',a1) for i in linspace(0,360,50)])
l1=plos(s1,c23(star),[0,0,1])
l1_1=plos(s1,c23(offset(star,-5)),[0,0,1])
l1_2=translate([0,0,-5],l1)
l2=c23(star)
l2_1=c23(offset(star,-5))
l2_2=translate([0,0,5],l2)
s2=cpo(convert_3lines2fillet(l2_1,l2_2,l2,s=20))[:-1]
s3=cpo(convert_3lines2fillet(l1_2,l1_1,l1,s=20))[:-1]
s4=s2+s3
l3=c23([offset(star,-i) for i in linspace(5.2,15.5,10)])
s5=psos(s1,l3,[0,0,1])
s4=flip(l3)+s4+s5
with open('trial.scad','w+') as f:
f.write(f'''
{swp(s4)}
''')
results:
[image: Screenshot 2024-12-26 at 10.27.07 PM.png]
[image: Screenshot 2024-12-26 at 10.29.36 PM.png]
[image: Screenshot 2024-12-26 at 10.30.47 PM.png]
On Thu, 26 Dec 2024 at 21:56, Thomas Richter via Discuss <
discuss@lists.openscad.org> wrote:
Thank you for your insights. I get good results printing the rounded
surface upside down and sanding it. You are right about the distance of
the top layers, this tends to be visible the closer it gets to flat, but
it's fine after sanding. Nonetheless, if you take a look at printables,
there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds for
brass castings.
The tangents of the tips and the notches actually match in both the
version on printables (made with boolean operations) and the analytical
version posted in this thread. The small edgy stripes between tips and
notches are subject to low $fn values of the cylinders when creating the
knob with boolean operations. With an analytically generated outline they
don't appear at all. Could you please elaborate on the problems you
experienced?
I make good progress creating the rounded top analytically. I generate a
polyhedron from several layers of outlines with the radius changing with
the cosine of the current step's angle. It is fast as hell, even with 360
steps around the edge it takes less than 50 milliseconds for two layers and
I expect to be fine with about ten layers for the rounded edge. I can post
the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this thread
are strangely shaped faces at the rounded edge after doing the minkowski.
The Prusa Slicer finds 20 errors in the resulting stl. This will also
disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss <
I'm not sure what Ray has against rounded edges. I use them all the
time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual
dome top of the knob, which tends to have a very exposed layer line
step-structure with very wide and visible steps that I think look and feel
pretty bad. That will be worse the closer you are to flat---I don't know
how bad it would look with the model as shown. I printed a knob to go on
my audio amp and my first version had a domed top like shown and I
scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside
down. That needs to be a chamfer or teardrop for the best result. So I'd
probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20,
bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix,
which is the corners where the tip circles meet the notch circles. For a
truly beautiful knob the tangents should match so that you don't have
corners there.
Oh, and one other thing that will make this faster no matter how you
proceed is to stop using so many points. The smallest facet is 0.22 mm in
the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic
method. You'd need to form a grid over the top of the knob to form the
polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and
bottom:
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will
ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges
will look awful. Minkowski is slow, especially if $fn is large. I would
suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad
children) some simple bevel modules. (They sliced at 0.1mm intervals, but
that and the profile could be varied). It gives much faster results than
using Minkowski. Basically, you could draw the profile of the knob in 2d,
linear extrude it to the desired thickness, then apply the bevel/rounding
modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I
think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com
wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems
with not closed mesh) but a different problem. Should I have asked in the
old thread anyway?
I create star shaped knobs for hex screws (see
https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
The rounded top surface is achieved by subtracting from a large sphere (see
prototype code below) and the rounded edges are created with the minkowski
sum. Since the sphere must be large for a low rounding it needs a large $fn
value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3
CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star
shape analytically instead of using unions and differences. This way I was
able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time
even further? The reason: I create a web based configuration tool and would
like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of
arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org