
TR
Thomas Richter
Thu, Dec 26, 2024 5:31 PM
Oh, I see. I never tested with that high values of the arm pitch. That is a stepping problem: The outline of the shape is generated in a for loop. Imagine that a beam turns counterclockwise around the z-axis in the xy plane in steps of one degree. For every step the radius of the outer shape is calculated and the corresponding point (the intersection of the beam and the outline) on the xy plane becomes part of the points array of the polygon forming the outer shape. At the positions you mention a step of one degree leads to a quite large step along the outline because at those positions the "beam" is almost parallel to the outline. If you reduce the step in the for loop from 1 to 0.1 this disappears. But that would lead to huge numbers of faces. So maybe in the future I will compensate for that with smaller steps at certain positions depending on the scalar product of the current outline and the "beam".
I understand your comments. This thing has developed its own life, currently going way further than it was intended in the first place, more and more becoming an intellectual game. Nonetheless, many people in my university's fab lab are quite happy I made and shared this.
Currently, I learn a lot about analytical geometry (actually re-memorizing things learnt decades ago in school) and about for me so far unknown ways to produce things in OpenSCAD. I could have let it go a long time ago, but the challenge of learning and speeding up the calculation now really appeals to me.
Although the calculations may look confusing, it is mainly just the application of the sine and cosine theorems to scalene triangles.
Am 26.12.2024 um 17:57 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
Sanding well enough to produce a model that looks good is going to be a ton of work---more work than I would put forth for a model. Casting is obviously a different application, where appearance doesn't matter. But if you're planning to offer a generator to people, I would guess most people are in my camp: no interest in a bunch of post processing of the model. If I had a project with 8 knobs it would loom even larger as a nuisance. What would make sense for this is solvent smoothing...but I don't do that either. (Not really feasible with PLA.)
Building structures analytically is generally very fast if you have a reasonably straight forward analytic approach. I can't quite understand your method to know what the result would look like---definitely post your final result.
Regarding the corners, it's not super visible in the model as you gave it, but when I changed armPitch to 3 I got this<image.png>
The corner is very clear here. So if your math is producing a corner when armPitch=3 then most likely there is exactly one value of armPitch (other parameters held fixed) that generates a model where the tangents match and there is no corner. I didn't try to understand your code enough to know what's going on there. The corner is more subtle with less extreme parameter choices, but may be tactile even if not obvious in the model on screen.
At armPitch of 3.2 there are now two obvious corners:
<image.png>
And these parameter values seem plausible use cases, not crazy outlier values, so if you're providing a parameterized model it seems like they should work.
On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss discuss@lists.openscad.org wrote:
Thank you for your insights. I get good results printing the rounded surface upside down and sanding it. You are right about the distance of the top layers, this tends to be visible the closer it gets to flat, but it's fine after sanding. Nonetheless, if you take a look at printables, there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds for brass castings.
The tangents of the tips and the notches actually match in both the version on printables (made with boolean operations) and the analytical version posted in this thread. The small edgy stripes between tips and notches are subject to low $fn values of the cylinders when creating the knob with boolean operations. With an analytically generated outline they don't appear at all. Could you please elaborate on the problems you experienced?
I make good progress creating the rounded top analytically. I generate a polyhedron from several layers of outlines with the radius changing with the cosine of the current step's angle. It is fast as hell, even with 360 steps around the edge it takes less than 50 milliseconds for two layers and I expect to be fine with about ten layers for the rounded edge. I can post the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this thread are strangely shaped faces at the rounded edge after doing the minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will also disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside down. That needs to be a chamfer or teardrop for the best result. So I'd probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix, which is the corners where the tip circles meet the notch circles. For a truly beautiful knob the tangents should match so that you don't have corners there.
Oh, and one other thing that will make this faster no matter how you proceed is to stop using so many points. The smallest facet is 0.22 mm in the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic method. You'd need to form a grid over the top of the knob to form the polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and bottom:
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss discuss@lists.openscad.org wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges will look awful. Minkowski is slow, especially if $fn is large. I would suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad children) some simple bevel modules. (They sliced at 0.1mm intervals, but that and the profile could be varied). It gives much faster results than using Minkowski. Basically, you could draw the profile of the knob in 2d, linear extrude it to the desired thickness, then apply the bevel/rounding modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Oh, I see. I never tested with that high values of the arm pitch. That is a stepping problem: The outline of the shape is generated in a for loop. Imagine that a beam turns counterclockwise around the z-axis in the xy plane in steps of one degree. For every step the radius of the outer shape is calculated and the corresponding point (the intersection of the beam and the outline) on the xy plane becomes part of the points array of the polygon forming the outer shape. At the positions you mention a step of one degree leads to a quite large step along the outline because at those positions the "beam" is almost parallel to the outline. If you reduce the step in the for loop from 1 to 0.1 this disappears. But that would lead to huge numbers of faces. So maybe in the future I will compensate for that with smaller steps at certain positions depending on the scalar product of the current outline and the "beam".
I understand your comments. This thing has developed its own life, currently going way further than it was intended in the first place, more and more becoming an intellectual game. Nonetheless, many people in my university's fab lab are quite happy I made and shared this.
Currently, I learn a lot about analytical geometry (actually re-memorizing things learnt decades ago in school) and about for me so far unknown ways to produce things in OpenSCAD. I could have let it go a long time ago, but the challenge of learning and speeding up the calculation now really appeals to me.
Although the calculations may look confusing, it is mainly just the application of the sine and cosine theorems to scalene triangles.
> Am 26.12.2024 um 17:57 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
>
> Sanding well enough to produce a model that looks good is going to be a ton of work---more work than I would put forth for a model. Casting is obviously a different application, where appearance doesn't matter. But if you're planning to offer a generator to people, I would guess most people are in my camp: no interest in a bunch of post processing of the model. If I had a project with 8 knobs it would loom even larger as a nuisance. What would make sense for this is solvent smoothing...but I don't do that either. (Not really feasible with PLA.)
>
> Building structures analytically is generally very fast if you have a reasonably straight forward analytic approach. I can't quite understand your method to know what the result would look like---definitely post your final result.
>
> Regarding the corners, it's not super visible in the model as you gave it, but when I changed armPitch to 3 I got this<image.png>
>
>
> The corner is very clear here. So if your math is producing a corner when armPitch=3 then most likely there is exactly one value of armPitch (other parameters held fixed) that generates a model where the tangents match and there is no corner. I didn't try to understand your code enough to know what's going on there. The corner is more subtle with less extreme parameter choices, but may be tactile even if not obvious in the model on screen.
>
> At armPitch of 3.2 there are now two obvious corners:
>
> <image.png>
>
> And these parameter values seem plausible use cases, not crazy outlier values, so if you're providing a parameterized model it seems like they should work.
>
> On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss <discuss@lists.openscad.org> wrote:
> Thank you for your insights. I get good results printing the rounded surface upside down _and sanding_ it. You are right about the distance of the top layers, this tends to be visible the closer it gets to flat, but it's fine after sanding. Nonetheless, if you take a look at printables, there are also flat versions of the knobs.
>
> I don't just print the knobs but use the sanded prints to create molds for brass castings.
>
> The tangents of the tips and the notches actually match in both the version on printables (made with boolean operations) and the analytical version posted in this thread. The small edgy stripes between tips and notches are subject to low $fn values of the cylinders when creating the knob with boolean operations. With an analytically generated outline they don't appear at all. Could you please elaborate on the problems you experienced?
>
> I make good progress creating the rounded top analytically. I generate a polyhedron from several layers of outlines with the radius changing with the cosine of the current step's angle. It is fast as hell, even with 360 steps around the edge it takes less than 50 milliseconds for two layers and I expect to be fine with about ten layers for the rounded edge. I can post the solution here later if someone is interested.
>
> One interesting thing I noticed with the solution I posted in this thread are strangely shaped faces at the rounded edge after doing the minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will also disappear with the analytical solution.
>
>
> > Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
> >
> > I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
> >
> > What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
> >
> > The other thing that does NOT look great is a roundover printed upside down. That needs to be a chamfer or teardrop for the best result. So I'd probably do something like this for a flat topped model:
> >
> > include<BOSL2/std.scad>
> > include<BOSL2/rounding.scad>
> > offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
> >
> > to get that effect. There is another thing I'd probably try to fix, which is the corners where the tip circles meet the notch circles. For a truly beautiful knob the tangents should match so that you don't have corners there.
> >
> > Oh, and one other thing that will make this faster no matter how you proceed is to stop using so many points. The smallest facet is 0.22 mm in the posted version. That's unnecessarily small.
> >
> > I don't see an easy way to create the original shape using an analytic method. You'd need to form a grid over the top of the knob to form the polyhedral face of the top, and that seems pretty difficult to do.
> >
> > Here's what the knot from the above code looks like from the top and bottom:
> >
> > <image.png>
> >
> > <image.png>
> > Avoiding the lower angle at the bottom by switching to a chamfer will ensure good printing.
> >
> > On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <discuss@lists.openscad.org> wrote:
> > If the knob is to be 3d fdm printed by others, then the rounded edges will look awful. Minkowski is slow, especially if $fn is large. I would suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad children) some simple bevel modules. (They sliced at 0.1mm intervals, but that and the profile could be varied). It gives much faster results than using Minkowski. Basically, you could draw the profile of the knob in 2d, linear extrude it to the desired thickness, then apply the bevel/rounding modules.
> > On 26/12/2024 08:12, pca006132 via Discuss wrote:
> >> Another way would be to do the convex decomposition by yourself, I think it can be split into 5 convex components?
> >>
> >> On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM <john.lck40@gmail.com> wrote:
> >> The slowness is really in the CGAL convex decomposition code path, and
> >> sadly there is no plan to make a faster one for now.
> >>
> >> If you want this to be fast, the best way might be to do it
> >> analytically, considering you already computed the knob outline
> >> analytically, it may not be that hard.
> >>
> >> On 12/26/24 15:53, Thomas Richter via Discuss wrote:
> >> > This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
> >> >
> >> > I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
> >> >
> >> > This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
> >> >
> >> > Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
> >> >
> >> > /**
> >> > * prototype code
> >> > */
> >> > ARMS = 5;
> >> >
> >> > // knobDiameter
> >> > kd = 40;
> >> > rKnob = kd / 2;
> >> > // armPitch
> >> > ap = 2;
> >> > // notchRatio
> >> > nr = 3;
> >> >
> >> > // radius of the arm circles
> >> > rK = PI * rKnob / ((ap + 1) * ARMS + PI);
> >> > // radius of the notch circles
> >> > rN = nr * rK;
> >> >
> >> > // radius of the circle to place the arms (rbk)
> >> > rPosK = rKnob - rK;
> >> >
> >> > // angle between arm and notch (360 / ARMS / 2)
> >> > alpha = 180 / ARMS;
> >> >
> >> > // angle between center of knob, center of notch, center of arm
> >> > gamma = asin(sin(alpha) * rPosK / (rN + rK));
> >> >
> >> > // angle between center of knob, center of arm, center of notch
> >> > beta = 180 - alpha - gamma;
> >> >
> >> > // radius of the circle to place the notches (rbn)
> >> > rPosN = abs(rPosK * sin(beta) / sin(gamma));
> >> >
> >> > // radius of the knob's core: distance from center to touch point of arm and notch (rc)
> >> > rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
> >> >
> >> > // angle to touch point
> >> > alphaC = asin(rK * sin(beta) / rCore);
> >> >
> >> > armAngle = 360 / ARMS;
> >> >
> >> > points = [
> >> >
> >> > for (phi = [0: 1: 360])
> >> > let (arm = floor(phi / armAngle))
> >> > let (phiTemp = phi - (arm * armAngle))
> >> > // only half of an arm is uniquely defined, the rest can be determined
> >> > // by rotation and mirroring
> >> > let (phiNorm = phiTemp > armAngle / 2
> >> > ? armAngle - phiTemp
> >> > : phiTemp)
> >> > let (rx = abs(phiNorm) < 1e-6
> >> > ? rKnob
> >> > : abs(phiNorm - armAngle / 2) < 1e-6
> >> > ? rPosN - rN
> >> > : phiNorm < alphaC
> >> > ?
> >> > let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
> >> > let (beta2 = 180 - phiNorm - gamma2)
> >> > rK * sin(beta2) / sin(phiNorm)
> >> > :
> >> > let (delta = alpha - phiNorm)
> >> > let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
> >> > let (rho = 180 - delta - epsilon)
> >> > rN * sin(rho) / sin(delta)
> >> > )
> >> >
> >> > [rx * cos(phi), rx * sin(phi)]
> >> > ];
> >> >
> >> > // quick and dirty prototype for testing
> >> > minkowski() {
> >> > sphere(2, $fn = 36);
> >> >
> >> > difference() {
> >> > translate([0, 0, -30]) sphere(d = 99, $fn = 120);
> >> >
> >> > difference () {
> >> > translate([0, 0, -35]) cube(110, center = true);
> >> >
> >> > linear_extrude(20) polygon(points);
> >> > }
> >> > }
> >> > }
> >> > _______________________________________________
> >> > OpenSCAD mailing list
> >> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> >>
> >> _______________________________________________
> >> OpenSCAD mailing list
> >> To unsubscribe send an email to discuss-leave@lists.openscad.org
> >>
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

RW
Raymond West
Thu, Dec 26, 2024 7:00 PM
On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
I'm not sure what Ray has against rounded edges. I use them all the
time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the
gradual dome top of the knob, which tends to have a very exposed layer
line step-structure with very wide and visible steps that I think look
and feel pretty bad. That will be worse the closer you are to
flat---I don't know how bad it would look with the model as shown. I
printed a knob to go on my audio amp and my first version had a domed
top like shown and I scratched that and went back to flat after I felt
the model in hand.
The other thing that does NOT look great is a roundover printed upside
down.
Hi Adrian, you half answered your own question to me, and nop head gave
the top half answer, wrt adaptive.
On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
> I'm not sure what Ray has against rounded edges. I use them all the
> time and think they look and feel great in my FDM printed models.
>
> What does NOT look great in my experience is something like the
> gradual dome top of the knob, which tends to have a very exposed layer
> line step-structure with very wide and visible steps that I think look
> and feel pretty bad. That will be worse the closer you are to
> flat---I don't know how bad it would look with the model as shown. I
> printed a knob to go on my audio amp and my first version had a domed
> top like shown and I scratched that and went back to flat after I felt
> the model in hand.
>
> The other thing that does NOT look great is a roundover printed upside
> down.
>
Hi Adrian, you half answered your own question to me, and nop head gave
the top half answer, wrt adaptive.

AM
Adrian Mariano
Thu, Dec 26, 2024 7:02 PM
I tried jacking up the sample rate and indeed it looks smoother, but to my
eye it appears that there is still a corner. But maybe I'm imagining it.
It's a pretty subtle corner if it's real, so it probably doesn't matter.
You are mating two curves, one when phiNorm<alphaC and one when
phiNorm>=alphaC. Have you designed them to have matching tangents?
But to eliminate the visual corners without going crazy on sample rate I
think you need to change your sampling method to sample the two arcs
separately and then join them. That way the arcs can be sampled uniformly
over their length instead of sampled based on the global polar coordinate
and the sample rate will be appropriate for the curvature of each part.
This will fix the sampled problems created by using global polar
coordinates, which obviously doesn't work properly for knobs with thinner
or concave arms. The code for what I propose is actually probably simpler
if the design is indeed two circular arcs. (I can't tell on brief
inspection what that code is doing.)
On Thu, Dec 26, 2024 at 12:31 PM Thomas Richter via Discuss <
discuss@lists.openscad.org> wrote:
Oh, I see. I never tested with that high values of the arm pitch. That is
a stepping problem: The outline of the shape is generated in a for loop.
Imagine that a beam turns counterclockwise around the z-axis in the xy
plane in steps of one degree. For every step the radius of the outer shape
is calculated and the corresponding point (the intersection of the beam and
the outline) on the xy plane becomes part of the points array of the
polygon forming the outer shape. At the positions you mention a step of one
degree leads to a quite large step along the outline because at those
positions the "beam" is almost parallel to the outline. If you reduce the
step in the for loop from 1 to 0.1 this disappears. But that would lead to
huge numbers of faces. So maybe in the future I will compensate for that
with smaller steps at certain positions depending on the scalar product of
the current outline and the "beam".
I understand your comments. This thing has developed its own life,
currently going way further than it was intended in the first place, more
and more becoming an intellectual game. Nonetheless, many people in my
university's fab lab are quite happy I made and shared this.
Currently, I learn a lot about analytical geometry (actually re-memorizing
things learnt decades ago in school) and about for me so far unknown ways
to produce things in OpenSCAD. I could have let it go a long time ago, but
the challenge of learning and speeding up the calculation now really
appeals to me.
Although the calculations may look confusing, it is mainly just the
application of the sine and cosine theorems to scalene triangles.
Am 26.12.2024 um 17:57 schrieb Adrian Mariano via Discuss <
Sanding well enough to produce a model that looks good is going to be a
ton of work---more work than I would put forth for a model. Casting is
obviously a different application, where appearance doesn't matter. But if
you're planning to offer a generator to people, I would guess most people
are in my camp: no interest in a bunch of post processing of the model. If
I had a project with 8 knobs it would loom even larger as a nuisance. What
would make sense for this is solvent smoothing...but I don't do that
either. (Not really feasible with PLA.)
Building structures analytically is generally very fast if you have a
reasonably straight forward analytic approach. I can't quite understand
your method to know what the result would look like---definitely post your
final result.
Regarding the corners, it's not super visible in the model as you gave
it, but when I changed armPitch to 3 I got this<image.png>
The corner is very clear here. So if your math is producing a corner
when armPitch=3 then most likely there is exactly one value of armPitch
(other parameters held fixed) that generates a model where the tangents
match and there is no corner. I didn't try to understand your code enough
to know what's going on there. The corner is more subtle with less
extreme parameter choices, but may be tactile even if not obvious in the
model on screen.
At armPitch of 3.2 there are now two obvious corners:
<image.png>
And these parameter values seem plausible use cases, not crazy outlier
values, so if you're providing a parameterized model it seems like they
should work.
On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss <
Thank you for your insights. I get good results printing the rounded
surface upside down and sanding it. You are right about the distance of
the top layers, this tends to be visible the closer it gets to flat, but
it's fine after sanding. Nonetheless, if you take a look at printables,
there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds
The tangents of the tips and the notches actually match in both the
version on printables (made with boolean operations) and the analytical
version posted in this thread. The small edgy stripes between tips and
notches are subject to low $fn values of the cylinders when creating the
knob with boolean operations. With an analytically generated outline they
don't appear at all. Could you please elaborate on the problems you
experienced?
I make good progress creating the rounded top analytically. I generate a
polyhedron from several layers of outlines with the radius changing with
the cosine of the current step's angle. It is fast as hell, even with 360
steps around the edge it takes less than 50 milliseconds for two layers and
I expect to be fine with about ten layers for the rounded edge. I can post
the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this
thread are strangely shaped faces at the rounded edge after doing the
minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will
also disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss <
I'm not sure what Ray has against rounded edges. I use them all the
time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the
gradual dome top of the knob, which tends to have a very exposed layer line
step-structure with very wide and visible steps that I think look and feel
pretty bad. That will be worse the closer you are to flat---I don't know
how bad it would look with the model as shown. I printed a knob to go on
my audio amp and my first version had a domed top like shown and I
scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside
down. That needs to be a chamfer or teardrop for the best result. So I'd
probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20,
bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix,
which is the corners where the tip circles meet the notch circles. For a
truly beautiful knob the tangents should match so that you don't have
corners there.
Oh, and one other thing that will make this faster no matter how you
proceed is to stop using so many points. The smallest facet is 0.22 mm in
the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic
method. You'd need to form a grid over the top of the knob to form the
polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <
If the knob is to be 3d fdm printed by others, then the rounded edges
will look awful. Minkowski is slow, especially if $fn is large. I would
suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad
children) some simple bevel modules. (They sliced at 0.1mm intervals, but
that and the profile could be varied). It gives much faster results than
using Minkowski. Basically, you could draw the profile of the knob in 2d,
linear extrude it to the desired thickness, then apply the bevel/rounding
modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I
think it can be split into 5 convex components?
The slowness is really in the CGAL convex decomposition code path,
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago
(problems with not closed mesh) but a different problem. Should I have
asked in the old thread anyway?
I create star shaped knobs for hex screws (see
This is already an optimized version since I create the basic star
shape analytically instead of using unions and differences. This way I was
able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing
time even further? The reason: I create a web based configuration tool and
would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I tried jacking up the sample rate and indeed it looks smoother, but to my
eye it appears that there is still a corner. But maybe I'm imagining it.
It's a pretty subtle corner if it's real, so it probably doesn't matter.
You are mating two curves, one when phiNorm<alphaC and one when
phiNorm>=alphaC. Have you designed them to have matching tangents?
But to eliminate the visual corners without going crazy on sample rate I
think you need to change your sampling method to sample the two arcs
separately and then join them. That way the arcs can be sampled uniformly
over their length instead of sampled based on the global polar coordinate
and the sample rate will be appropriate for the curvature of each part.
This will fix the sampled problems created by using global polar
coordinates, which obviously doesn't work properly for knobs with thinner
or concave arms. The code for what I propose is actually probably simpler
if the design is indeed two circular arcs. (I can't tell on brief
inspection what that code is doing.)
On Thu, Dec 26, 2024 at 12:31 PM Thomas Richter via Discuss <
discuss@lists.openscad.org> wrote:
> Oh, I see. I never tested with that high values of the arm pitch. That is
> a stepping problem: The outline of the shape is generated in a for loop.
> Imagine that a beam turns counterclockwise around the z-axis in the xy
> plane in steps of one degree. For every step the radius of the outer shape
> is calculated and the corresponding point (the intersection of the beam and
> the outline) on the xy plane becomes part of the points array of the
> polygon forming the outer shape. At the positions you mention a step of one
> degree leads to a quite large step along the outline because at those
> positions the "beam" is almost parallel to the outline. If you reduce the
> step in the for loop from 1 to 0.1 this disappears. But that would lead to
> huge numbers of faces. So maybe in the future I will compensate for that
> with smaller steps at certain positions depending on the scalar product of
> the current outline and the "beam".
>
> I understand your comments. This thing has developed its own life,
> currently going way further than it was intended in the first place, more
> and more becoming an intellectual game. Nonetheless, many people in my
> university's fab lab are quite happy I made and shared this.
>
> Currently, I learn a lot about analytical geometry (actually re-memorizing
> things learnt decades ago in school) and about for me so far unknown ways
> to produce things in OpenSCAD. I could have let it go a long time ago, but
> the challenge of learning and speeding up the calculation now really
> appeals to me.
>
> Although the calculations may look confusing, it is mainly just the
> application of the sine and cosine theorems to scalene triangles.
>
> > Am 26.12.2024 um 17:57 schrieb Adrian Mariano via Discuss <
> discuss@lists.openscad.org>:
> >
> > Sanding well enough to produce a model that looks good is going to be a
> ton of work---more work than I would put forth for a model. Casting is
> obviously a different application, where appearance doesn't matter. But if
> you're planning to offer a generator to people, I would guess most people
> are in my camp: no interest in a bunch of post processing of the model. If
> I had a project with 8 knobs it would loom even larger as a nuisance. What
> would make sense for this is solvent smoothing...but I don't do that
> either. (Not really feasible with PLA.)
> >
> > Building structures analytically is generally very fast if you have a
> reasonably straight forward analytic approach. I can't quite understand
> your method to know what the result would look like---definitely post your
> final result.
> >
> > Regarding the corners, it's not super visible in the model as you gave
> it, but when I changed armPitch to 3 I got this<image.png>
> >
> >
> > The corner is very clear here. So if your math is producing a corner
> when armPitch=3 then most likely there is exactly one value of armPitch
> (other parameters held fixed) that generates a model where the tangents
> match and there is no corner. I didn't try to understand your code enough
> to know what's going on there. The corner is more subtle with less
> extreme parameter choices, but may be tactile even if not obvious in the
> model on screen.
> >
> > At armPitch of 3.2 there are now two obvious corners:
> >
> > <image.png>
> >
> > And these parameter values seem plausible use cases, not crazy outlier
> values, so if you're providing a parameterized model it seems like they
> should work.
> >
> > On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss <
> discuss@lists.openscad.org> wrote:
> > Thank you for your insights. I get good results printing the rounded
> surface upside down _and sanding_ it. You are right about the distance of
> the top layers, this tends to be visible the closer it gets to flat, but
> it's fine after sanding. Nonetheless, if you take a look at printables,
> there are also flat versions of the knobs.
> >
> > I don't just print the knobs but use the sanded prints to create molds
> for brass castings.
> >
> > The tangents of the tips and the notches actually match in both the
> version on printables (made with boolean operations) and the analytical
> version posted in this thread. The small edgy stripes between tips and
> notches are subject to low $fn values of the cylinders when creating the
> knob with boolean operations. With an analytically generated outline they
> don't appear at all. Could you please elaborate on the problems you
> experienced?
> >
> > I make good progress creating the rounded top analytically. I generate a
> polyhedron from several layers of outlines with the radius changing with
> the cosine of the current step's angle. It is fast as hell, even with 360
> steps around the edge it takes less than 50 milliseconds for two layers and
> I expect to be fine with about ten layers for the rounded edge. I can post
> the solution here later if someone is interested.
> >
> > One interesting thing I noticed with the solution I posted in this
> thread are strangely shaped faces at the rounded edge after doing the
> minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will
> also disappear with the analytical solution.
> >
> >
> > > Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss <
> discuss@lists.openscad.org>:
> > >
> > > I'm not sure what Ray has against rounded edges. I use them all the
> time and think they look and feel great in my FDM printed models.
> > >
> > > What does NOT look great in my experience is something like the
> gradual dome top of the knob, which tends to have a very exposed layer line
> step-structure with very wide and visible steps that I think look and feel
> pretty bad. That will be worse the closer you are to flat---I don't know
> how bad it would look with the model as shown. I printed a knob to go on
> my audio amp and my first version had a domed top like shown and I
> scratched that and went back to flat after I felt the model in hand.
> > >
> > > The other thing that does NOT look great is a roundover printed upside
> down. That needs to be a chamfer or teardrop for the best result. So I'd
> probably do something like this for a flat topped model:
> > >
> > > include<BOSL2/std.scad>
> > > include<BOSL2/rounding.scad>
> > > offset_sweep(deduplicate(points,closed=true), h=20,
> bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
> > >
> > > to get that effect. There is another thing I'd probably try to fix,
> which is the corners where the tip circles meet the notch circles. For a
> truly beautiful knob the tangents should match so that you don't have
> corners there.
> > >
> > > Oh, and one other thing that will make this faster no matter how you
> proceed is to stop using so many points. The smallest facet is 0.22 mm in
> the posted version. That's unnecessarily small.
> > >
> > > I don't see an easy way to create the original shape using an analytic
> method. You'd need to form a grid over the top of the knob to form the
> polyhedral face of the top, and that seems pretty difficult to do.
> > >
> > > Here's what the knot from the above code looks like from the top and
> bottom:
> > >
> > > <image.png>
> > >
> > > <image.png>
> > > Avoiding the lower angle at the bottom by switching to a chamfer will
> ensure good printing.
> > >
> > > On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <
> discuss@lists.openscad.org> wrote:
> > > If the knob is to be 3d fdm printed by others, then the rounded edges
> will look awful. Minkowski is slow, especially if $fn is large. I would
> suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad
> children) some simple bevel modules. (They sliced at 0.1mm intervals, but
> that and the profile could be varied). It gives much faster results than
> using Minkowski. Basically, you could draw the profile of the knob in 2d,
> linear extrude it to the desired thickness, then apply the bevel/rounding
> modules.
> > > On 26/12/2024 08:12, pca006132 via Discuss wrote:
> > >> Another way would be to do the convex decomposition by yourself, I
> think it can be split into 5 convex components?
> > >>
> > >> On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM <john.lck40@gmail.com>
> wrote:
> > >> The slowness is really in the CGAL convex decomposition code path,
> and
> > >> sadly there is no plan to make a faster one for now.
> > >>
> > >> If you want this to be fast, the best way might be to do it
> > >> analytically, considering you already computed the knob outline
> > >> analytically, it may not be that hard.
> > >>
> > >> On 12/26/24 15:53, Thomas Richter via Discuss wrote:
> > >> > This is related to a question I asked a couple of days ago
> (problems with not closed mesh) but a different problem. Should I have
> asked in the old thread anyway?
> > >> >
> > >> > I create star shaped knobs for hex screws (see
> https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau).
> The rounded top surface is achieved by subtracting from a large sphere (see
> prototype code below) and the rounded edges are created with the minkowski
> sum. Since the sphere must be large for a low rounding it needs a large $fn
> value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3
> CPU) to generate the object with manifold backend.
> > >> >
> > >> > This is already an optimized version since I create the basic star
> shape analytically instead of using unions and differences. This way I was
> able to reduce the computing time by about 80% already.
> > >> >
> > >> > Does someone here have an idea how I could reduce the computing
> time even further? The reason: I create a web based configuration tool and
> would like to provide the stl file in less than ten seconds.
> > >> >
> > >> > /**
> > >> > * prototype code
> > >> > */
> > >> > ARMS = 5;
> > >> >
> > >> > // knobDiameter
> > >> > kd = 40;
> > >> > rKnob = kd / 2;
> > >> > // armPitch
> > >> > ap = 2;
> > >> > // notchRatio
> > >> > nr = 3;
> > >> >
> > >> > // radius of the arm circles
> > >> > rK = PI * rKnob / ((ap + 1) * ARMS + PI);
> > >> > // radius of the notch circles
> > >> > rN = nr * rK;
> > >> >
> > >> > // radius of the circle to place the arms (rbk)
> > >> > rPosK = rKnob - rK;
> > >> >
> > >> > // angle between arm and notch (360 / ARMS / 2)
> > >> > alpha = 180 / ARMS;
> > >> >
> > >> > // angle between center of knob, center of notch, center of arm
> > >> > gamma = asin(sin(alpha) * rPosK / (rN + rK));
> > >> >
> > >> > // angle between center of knob, center of arm, center of notch
> > >> > beta = 180 - alpha - gamma;
> > >> >
> > >> > // radius of the circle to place the notches (rbn)
> > >> > rPosN = abs(rPosK * sin(beta) / sin(gamma));
> > >> >
> > >> > // radius of the knob's core: distance from center to touch point
> of arm and notch (rc)
> > >> > rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
> > >> >
> > >> > // angle to touch point
> > >> > alphaC = asin(rK * sin(beta) / rCore);
> > >> >
> > >> > armAngle = 360 / ARMS;
> > >> >
> > >> > points = [
> > >> >
> > >> > for (phi = [0: 1: 360])
> > >> > let (arm = floor(phi / armAngle))
> > >> > let (phiTemp = phi - (arm * armAngle))
> > >> > // only half of an arm is uniquely defined, the rest can be
> determined
> > >> > // by rotation and mirroring
> > >> > let (phiNorm = phiTemp > armAngle / 2
> > >> > ? armAngle - phiTemp
> > >> > : phiTemp)
> > >> > let (rx = abs(phiNorm) < 1e-6
> > >> > ? rKnob
> > >> > : abs(phiNorm - armAngle / 2) < 1e-6
> > >> > ? rPosN - rN
> > >> > : phiNorm < alphaC
> > >> > ?
> > >> > let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
> > >> > let (beta2 = 180 - phiNorm - gamma2)
> > >> > rK * sin(beta2) / sin(phiNorm)
> > >> > :
> > >> > let (delta = alpha - phiNorm)
> > >> > let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
> > >> > let (rho = 180 - delta - epsilon)
> > >> > rN * sin(rho) / sin(delta)
> > >> > )
> > >> >
> > >> > [rx * cos(phi), rx * sin(phi)]
> > >> > ];
> > >> >
> > >> > // quick and dirty prototype for testing
> > >> > minkowski() {
> > >> > sphere(2, $fn = 36);
> > >> >
> > >> > difference() {
> > >> > translate([0, 0, -30]) sphere(d = 99, $fn = 120);
> > >> >
> > >> > difference () {
> > >> > translate([0, 0, -35]) cube(110, center = true);
> > >> >
> > >> > linear_extrude(20) polygon(points);
> > >> > }
> > >> > }
> > >> > }
> > >> > _______________________________________________
> > >> > OpenSCAD mailing list
> > >> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > >>
> > >> _______________________________________________
> > >> OpenSCAD mailing list
> > >> To unsubscribe send an email to discuss-leave@lists.openscad.org
> > >>
> > > _______________________________________________
> > > OpenSCAD mailing list
> > > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > > _______________________________________________
> > > OpenSCAD mailing list
> > > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Thu, Dec 26, 2024 7:06 PM
Ray, are you saying it's only the upside-down rounded edges that you think
are "awful"? I don't really understand. I basically round every edge I
possibly can in my models---but that doesn't include upside-down ones.
I'll have to look into that adaptive layer thickness.
On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
I'm not sure what Ray has against rounded edges. I use them all the time
and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual
dome top of the knob, which tends to have a very exposed layer line
step-structure with very wide and visible steps that I think look and feel
pretty bad. That will be worse the closer you are to flat---I don't know
how bad it would look with the model as shown. I printed a knob to go on
my audio amp and my first version had a domed top like shown and I
scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside
down.
Hi Adrian, you half answered your own question to me, and nop head gave
the top half answer, wrt adaptive.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Ray, are you saying it's only the upside-down rounded edges that you think
are "awful"? I don't really understand. I basically round every edge I
possibly can in my models---but that doesn't include upside-down ones.
I'll have to look into that adaptive layer thickness.
On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:
>
> On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
>
> I'm not sure what Ray has against rounded edges. I use them all the time
> and think they look and feel great in my FDM printed models.
>
> What does NOT look great in my experience is something like the gradual
> dome top of the knob, which tends to have a very exposed layer line
> step-structure with very wide and visible steps that I think look and feel
> pretty bad. That will be worse the closer you are to flat---I don't know
> how bad it would look with the model as shown. I printed a knob to go on
> my audio amp and my first version had a domed top like shown and I
> scratched that and went back to flat after I felt the model in hand.
>
> The other thing that does NOT look great is a roundover printed upside
> down.
>
> Hi Adrian, you half answered your own question to me, and nop head gave
> the top half answer, wrt adaptive.
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

TR
Thomas Richter
Thu, Dec 26, 2024 7:30 PM
angleC is the polar(!) angle where the two circles touch: the circle that makes the tip / arm and the circle that makes the notch. So, they are tangent at that position. I need to switch the calculation method there because they have different radii and different orientiation (the notch circles' center ist outside the knob, the arms' is inside).
A couple days ago I had already made a solution using arcs instead of polar coordinates in Javascript and I will probably adapt this solution to OpenSCAD. It will make this problem disappear as you recommend. But currently I figure out the geometry of the top surface. Rounded edge works analytically already, rounded top surface is still to come. I have attached a screenshot of the current prototype. This renders in 87 milliseconds.
I am very grateful for the help from all of you.
Am 26.12.2024 um 20:02 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I tried jacking up the sample rate and indeed it looks smoother, but to my eye it appears that there is still a corner. But maybe I'm imagining it. It's a pretty subtle corner if it's real, so it probably doesn't matter. You are mating two curves, one when phiNorm<alphaC and one when phiNorm>=alphaC. Have you designed them to have matching tangents?
But to eliminate the visual corners without going crazy on sample rate I think you need to change your sampling method to sample the two arcs separately and then join them. That way the arcs can be sampled uniformly over their length instead of sampled based on the global polar coordinate and the sample rate will be appropriate for the curvature of each part. This will fix the sampled problems created by using global polar coordinates, which obviously doesn't work properly for knobs with thinner or concave arms. The code for what I propose is actually probably simpler if the design is indeed two circular arcs. (I can't tell on brief inspection what that code is doing.)
On Thu, Dec 26, 2024 at 12:31 PM Thomas Richter via Discuss discuss@lists.openscad.org wrote:
Oh, I see. I never tested with that high values of the arm pitch. That is a stepping problem: The outline of the shape is generated in a for loop. Imagine that a beam turns counterclockwise around the z-axis in the xy plane in steps of one degree. For every step the radius of the outer shape is calculated and the corresponding point (the intersection of the beam and the outline) on the xy plane becomes part of the points array of the polygon forming the outer shape. At the positions you mention a step of one degree leads to a quite large step along the outline because at those positions the "beam" is almost parallel to the outline. If you reduce the step in the for loop from 1 to 0.1 this disappears. But that would lead to huge numbers of faces. So maybe in the future I will compensate for that with smaller steps at certain positions depending on the scalar product of the current outline and the "beam".
I understand your comments. This thing has developed its own life, currently going way further than it was intended in the first place, more and more becoming an intellectual game. Nonetheless, many people in my university's fab lab are quite happy I made and shared this.
Currently, I learn a lot about analytical geometry (actually re-memorizing things learnt decades ago in school) and about for me so far unknown ways to produce things in OpenSCAD. I could have let it go a long time ago, but the challenge of learning and speeding up the calculation now really appeals to me.
Although the calculations may look confusing, it is mainly just the application of the sine and cosine theorems to scalene triangles.
Am 26.12.2024 um 17:57 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
Sanding well enough to produce a model that looks good is going to be a ton of work---more work than I would put forth for a model. Casting is obviously a different application, where appearance doesn't matter. But if you're planning to offer a generator to people, I would guess most people are in my camp: no interest in a bunch of post processing of the model. If I had a project with 8 knobs it would loom even larger as a nuisance. What would make sense for this is solvent smoothing...but I don't do that either. (Not really feasible with PLA.)
Building structures analytically is generally very fast if you have a reasonably straight forward analytic approach. I can't quite understand your method to know what the result would look like---definitely post your final result.
Regarding the corners, it's not super visible in the model as you gave it, but when I changed armPitch to 3 I got this<image.png>
The corner is very clear here. So if your math is producing a corner when armPitch=3 then most likely there is exactly one value of armPitch (other parameters held fixed) that generates a model where the tangents match and there is no corner. I didn't try to understand your code enough to know what's going on there. The corner is more subtle with less extreme parameter choices, but may be tactile even if not obvious in the model on screen.
At armPitch of 3.2 there are now two obvious corners:
<image.png>
And these parameter values seem plausible use cases, not crazy outlier values, so if you're providing a parameterized model it seems like they should work.
On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss discuss@lists.openscad.org wrote:
Thank you for your insights. I get good results printing the rounded surface upside down and sanding it. You are right about the distance of the top layers, this tends to be visible the closer it gets to flat, but it's fine after sanding. Nonetheless, if you take a look at printables, there are also flat versions of the knobs.
I don't just print the knobs but use the sanded prints to create molds for brass castings.
The tangents of the tips and the notches actually match in both the version on printables (made with boolean operations) and the analytical version posted in this thread. The small edgy stripes between tips and notches are subject to low $fn values of the cylinders when creating the knob with boolean operations. With an analytically generated outline they don't appear at all. Could you please elaborate on the problems you experienced?
I make good progress creating the rounded top analytically. I generate a polyhedron from several layers of outlines with the radius changing with the cosine of the current step's angle. It is fast as hell, even with 360 steps around the edge it takes less than 50 milliseconds for two layers and I expect to be fine with about ten layers for the rounded edge. I can post the solution here later if someone is interested.
One interesting thing I noticed with the solution I posted in this thread are strangely shaped faces at the rounded edge after doing the minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will also disappear with the analytical solution.
Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside down. That needs to be a chamfer or teardrop for the best result. So I'd probably do something like this for a flat topped model:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
to get that effect. There is another thing I'd probably try to fix, which is the corners where the tip circles meet the notch circles. For a truly beautiful knob the tangents should match so that you don't have corners there.
Oh, and one other thing that will make this faster no matter how you proceed is to stop using so many points. The smallest facet is 0.22 mm in the posted version. That's unnecessarily small.
I don't see an easy way to create the original shape using an analytic method. You'd need to form a grid over the top of the knob to form the polyhedral face of the top, and that seems pretty difficult to do.
Here's what the knot from the above code looks like from the top and bottom:
<image.png>
<image.png>
Avoiding the lower angle at the bottom by switching to a chamfer will ensure good printing.
On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss discuss@lists.openscad.org wrote:
If the knob is to be 3d fdm printed by others, then the rounded edges will look awful. Minkowski is slow, especially if $fn is large. I would suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad children) some simple bevel modules. (They sliced at 0.1mm intervals, but that and the profile could be varied). It gives much faster results than using Minkowski. Basically, you could draw the profile of the knob in 2d, linear extrude it to the desired thickness, then apply the bevel/rounding modules.
On 26/12/2024 08:12, pca006132 via Discuss wrote:
Another way would be to do the convex decomposition by yourself, I think it can be split into 5 convex components?
On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM john.lck40@gmail.com wrote:
The slowness is really in the CGAL convex decomposition code path, and
sadly there is no plan to make a faster one for now.
If you want this to be fast, the best way might be to do it
analytically, considering you already computed the knob outline
analytically, it may not be that hard.
On 12/26/24 15:53, Thomas Richter via Discuss wrote:
This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
/**
- prototype code
*/
ARMS = 5;
// knobDiameter
kd = 40;
rKnob = kd / 2;
// armPitch
ap = 2;
// notchRatio
nr = 3;
// radius of the arm circles
rK = PI * rKnob / ((ap + 1) * ARMS + PI);
// radius of the notch circles
rN = nr * rK;
// radius of the circle to place the arms (rbk)
rPosK = rKnob - rK;
// angle between arm and notch (360 / ARMS / 2)
alpha = 180 / ARMS;
// angle between center of knob, center of notch, center of arm
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of arm, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches (rbn)
rPosN = abs(rPosK * sin(beta) / sin(gamma));
// radius of the knob's core: distance from center to touch point of arm and notch (rc)
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
// angle to touch point
alphaC = asin(rK * sin(beta) / rCore);
armAngle = 360 / ARMS;
points = [
for (phi = [0: 1: 360])
let (arm = floor(phi / armAngle))
let (phiTemp = phi - (arm * armAngle))
// only half of an arm is uniquely defined, the rest can be determined
// by rotation and mirroring
let (phiNorm = phiTemp > armAngle / 2
? armAngle - phiTemp
: phiTemp)
let (rx = abs(phiNorm) < 1e-6
? rKnob
: abs(phiNorm - armAngle / 2) < 1e-6
? rPosN - rN
: phiNorm < alphaC
?
let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
let (beta2 = 180 - phiNorm - gamma2)
rK * sin(beta2) / sin(phiNorm)
:
let (delta = alpha - phiNorm)
let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
let (rho = 180 - delta - epsilon)
rN * sin(rho) / sin(delta)
)
[rx * cos(phi), rx * sin(phi)]
];
// quick and dirty prototype for testing
minkowski() {
sphere(2, $fn = 36);
difference() {
translate([0, 0, -30]) sphere(d = 99, $fn = 120);
difference () {
translate([0, 0, -35]) cube(110, center = true);
linear_extrude(20) polygon(points);
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
angleC is the polar(!) angle where the two circles touch: the circle that makes the tip / arm and the circle that makes the notch. So, they are tangent at that position. I need to switch the calculation method there because they have different radii and different orientiation (the notch circles' center ist outside the knob, the arms' is inside).
A couple days ago I had already made a solution using arcs instead of polar coordinates in Javascript and I will probably adapt this solution to OpenSCAD. It will make this problem disappear as you recommend. But currently I figure out the geometry of the top surface. Rounded edge works analytically already, rounded top surface is still to come. I have attached a screenshot of the current prototype. This renders in 87 milliseconds.
I am very grateful for the help from all of you.
> Am 26.12.2024 um 20:02 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
>
> I tried jacking up the sample rate and indeed it looks smoother, but to my eye it appears that there is still a corner. But maybe I'm imagining it. It's a pretty subtle corner if it's real, so it probably doesn't matter. You are mating two curves, one when phiNorm<alphaC and one when phiNorm>=alphaC. Have you designed them to have matching tangents?
>
> But to eliminate the visual corners without going crazy on sample rate I think you need to change your sampling method to sample the two arcs separately and then join them. That way the arcs can be sampled uniformly over their length instead of sampled based on the global polar coordinate and the sample rate will be appropriate for the curvature of each part. This will fix the sampled problems created by using global polar coordinates, which obviously doesn't work properly for knobs with thinner or concave arms. The code for what I propose is actually probably simpler if the design is indeed two circular arcs. (I can't tell on brief inspection what that code is doing.)
>
>
>
>
>
>
>
> On Thu, Dec 26, 2024 at 12:31 PM Thomas Richter via Discuss <discuss@lists.openscad.org> wrote:
> Oh, I see. I never tested with that high values of the arm pitch. That is a stepping problem: The outline of the shape is generated in a for loop. Imagine that a beam turns counterclockwise around the z-axis in the xy plane in steps of one degree. For every step the radius of the outer shape is calculated and the corresponding point (the intersection of the beam and the outline) on the xy plane becomes part of the points array of the polygon forming the outer shape. At the positions you mention a step of one degree leads to a quite large step along the outline because at those positions the "beam" is almost parallel to the outline. If you reduce the step in the for loop from 1 to 0.1 this disappears. But that would lead to huge numbers of faces. So maybe in the future I will compensate for that with smaller steps at certain positions depending on the scalar product of the current outline and the "beam".
>
> I understand your comments. This thing has developed its own life, currently going way further than it was intended in the first place, more and more becoming an intellectual game. Nonetheless, many people in my university's fab lab are quite happy I made and shared this.
>
> Currently, I learn a lot about analytical geometry (actually re-memorizing things learnt decades ago in school) and about for me so far unknown ways to produce things in OpenSCAD. I could have let it go a long time ago, but the challenge of learning and speeding up the calculation now really appeals to me.
>
> Although the calculations may look confusing, it is mainly just the application of the sine and cosine theorems to scalene triangles.
>
> > Am 26.12.2024 um 17:57 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
> >
> > Sanding well enough to produce a model that looks good is going to be a ton of work---more work than I would put forth for a model. Casting is obviously a different application, where appearance doesn't matter. But if you're planning to offer a generator to people, I would guess most people are in my camp: no interest in a bunch of post processing of the model. If I had a project with 8 knobs it would loom even larger as a nuisance. What would make sense for this is solvent smoothing...but I don't do that either. (Not really feasible with PLA.)
> >
> > Building structures analytically is generally very fast if you have a reasonably straight forward analytic approach. I can't quite understand your method to know what the result would look like---definitely post your final result.
> >
> > Regarding the corners, it's not super visible in the model as you gave it, but when I changed armPitch to 3 I got this<image.png>
> >
> >
> > The corner is very clear here. So if your math is producing a corner when armPitch=3 then most likely there is exactly one value of armPitch (other parameters held fixed) that generates a model where the tangents match and there is no corner. I didn't try to understand your code enough to know what's going on there. The corner is more subtle with less extreme parameter choices, but may be tactile even if not obvious in the model on screen.
> >
> > At armPitch of 3.2 there are now two obvious corners:
> >
> > <image.png>
> >
> > And these parameter values seem plausible use cases, not crazy outlier values, so if you're providing a parameterized model it seems like they should work.
> >
> > On Thu, Dec 26, 2024 at 11:26 AM Thomas Richter via Discuss <discuss@lists.openscad.org> wrote:
> > Thank you for your insights. I get good results printing the rounded surface upside down _and sanding_ it. You are right about the distance of the top layers, this tends to be visible the closer it gets to flat, but it's fine after sanding. Nonetheless, if you take a look at printables, there are also flat versions of the knobs.
> >
> > I don't just print the knobs but use the sanded prints to create molds for brass castings.
> >
> > The tangents of the tips and the notches actually match in both the version on printables (made with boolean operations) and the analytical version posted in this thread. The small edgy stripes between tips and notches are subject to low $fn values of the cylinders when creating the knob with boolean operations. With an analytically generated outline they don't appear at all. Could you please elaborate on the problems you experienced?
> >
> > I make good progress creating the rounded top analytically. I generate a polyhedron from several layers of outlines with the radius changing with the cosine of the current step's angle. It is fast as hell, even with 360 steps around the edge it takes less than 50 milliseconds for two layers and I expect to be fine with about ten layers for the rounded edge. I can post the solution here later if someone is interested.
> >
> > One interesting thing I noticed with the solution I posted in this thread are strangely shaped faces at the rounded edge after doing the minkowski. The Prusa Slicer finds 20 errors in the resulting stl. This will also disappear with the analytical solution.
> >
> >
> > > Am 26.12.2024 um 16:03 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
> > >
> > > I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
> > >
> > > What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
> > >
> > > The other thing that does NOT look great is a roundover printed upside down. That needs to be a chamfer or teardrop for the best result. So I'd probably do something like this for a flat topped model:
> > >
> > > include<BOSL2/std.scad>
> > > include<BOSL2/rounding.scad>
> > > offset_sweep(deduplicate(points,closed=true), h=20, bot=os_teardrop(r=2), top=os_circle(r=2),steps=9);
> > >
> > > to get that effect. There is another thing I'd probably try to fix, which is the corners where the tip circles meet the notch circles. For a truly beautiful knob the tangents should match so that you don't have corners there.
> > >
> > > Oh, and one other thing that will make this faster no matter how you proceed is to stop using so many points. The smallest facet is 0.22 mm in the posted version. That's unnecessarily small.
> > >
> > > I don't see an easy way to create the original shape using an analytic method. You'd need to form a grid over the top of the knob to form the polyhedral face of the top, and that seems pretty difficult to do.
> > >
> > > Here's what the knot from the above code looks like from the top and bottom:
> > >
> > > <image.png>
> > >
> > > <image.png>
> > > Avoiding the lower angle at the bottom by switching to a chamfer will ensure good printing.
> > >
> > > On Thu, Dec 26, 2024 at 7:21 AM Raymond West via Discuss <discuss@lists.openscad.org> wrote:
> > > If the knob is to be 3d fdm printed by others, then the rounded edges will look awful. Minkowski is slow, especially if $fn is large. I would suggest a redesign of the knob. I posted on here, a few weeks ago (re: bad children) some simple bevel modules. (They sliced at 0.1mm intervals, but that and the profile could be varied). It gives much faster results than using Minkowski. Basically, you could draw the profile of the knob in 2d, linear extrude it to the desired thickness, then apply the bevel/rounding modules.
> > > On 26/12/2024 08:12, pca006132 via Discuss wrote:
> > >> Another way would be to do the convex decomposition by yourself, I think it can be split into 5 convex components?
> > >>
> > >> On Thu, Dec 26, 2024, 4:07 PM Chun Kit LAM <john.lck40@gmail.com> wrote:
> > >> The slowness is really in the CGAL convex decomposition code path, and
> > >> sadly there is no plan to make a faster one for now.
> > >>
> > >> If you want this to be fast, the best way might be to do it
> > >> analytically, considering you already computed the knob outline
> > >> analytically, it may not be that hard.
> > >>
> > >> On 12/26/24 15:53, Thomas Richter via Discuss wrote:
> > >> > This is related to a question I asked a couple of days ago (problems with not closed mesh) but a different problem. Should I have asked in the old thread anyway?
> > >> >
> > >> > I create star shaped knobs for hex screws (see https://www.printables.com/model/1116311-parametric-knob-for-hex-nuts-and-allen-screws-knau). The rounded top surface is achieved by subtracting from a large sphere (see prototype code below) and the rounded edges are created with the minkowski sum. Since the sphere must be large for a low rounding it needs a large $fn value (120 currently). Thus, the minkowski sum needs about 80 seconds (M3 CPU) to generate the object with manifold backend.
> > >> >
> > >> > This is already an optimized version since I create the basic star shape analytically instead of using unions and differences. This way I was able to reduce the computing time by about 80% already.
> > >> >
> > >> > Does someone here have an idea how I could reduce the computing time even further? The reason: I create a web based configuration tool and would like to provide the stl file in less than ten seconds.
> > >> >
> > >> > /**
> > >> > * prototype code
> > >> > */
> > >> > ARMS = 5;
> > >> >
> > >> > // knobDiameter
> > >> > kd = 40;
> > >> > rKnob = kd / 2;
> > >> > // armPitch
> > >> > ap = 2;
> > >> > // notchRatio
> > >> > nr = 3;
> > >> >
> > >> > // radius of the arm circles
> > >> > rK = PI * rKnob / ((ap + 1) * ARMS + PI);
> > >> > // radius of the notch circles
> > >> > rN = nr * rK;
> > >> >
> > >> > // radius of the circle to place the arms (rbk)
> > >> > rPosK = rKnob - rK;
> > >> >
> > >> > // angle between arm and notch (360 / ARMS / 2)
> > >> > alpha = 180 / ARMS;
> > >> >
> > >> > // angle between center of knob, center of notch, center of arm
> > >> > gamma = asin(sin(alpha) * rPosK / (rN + rK));
> > >> >
> > >> > // angle between center of knob, center of arm, center of notch
> > >> > beta = 180 - alpha - gamma;
> > >> >
> > >> > // radius of the circle to place the notches (rbn)
> > >> > rPosN = abs(rPosK * sin(beta) / sin(gamma));
> > >> >
> > >> > // radius of the knob's core: distance from center to touch point of arm and notch (rc)
> > >> > rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
> > >> >
> > >> > // angle to touch point
> > >> > alphaC = asin(rK * sin(beta) / rCore);
> > >> >
> > >> > armAngle = 360 / ARMS;
> > >> >
> > >> > points = [
> > >> >
> > >> > for (phi = [0: 1: 360])
> > >> > let (arm = floor(phi / armAngle))
> > >> > let (phiTemp = phi - (arm * armAngle))
> > >> > // only half of an arm is uniquely defined, the rest can be determined
> > >> > // by rotation and mirroring
> > >> > let (phiNorm = phiTemp > armAngle / 2
> > >> > ? armAngle - phiTemp
> > >> > : phiTemp)
> > >> > let (rx = abs(phiNorm) < 1e-6
> > >> > ? rKnob
> > >> > : abs(phiNorm - armAngle / 2) < 1e-6
> > >> > ? rPosN - rN
> > >> > : phiNorm < alphaC
> > >> > ?
> > >> > let (gamma2 = asin(rPosK * sin(phiNorm) / rK))
> > >> > let (beta2 = 180 - phiNorm - gamma2)
> > >> > rK * sin(beta2) / sin(phiNorm)
> > >> > :
> > >> > let (delta = alpha - phiNorm)
> > >> > let (epsilon = 180 - asin(rPosN * sin(delta) / rN))
> > >> > let (rho = 180 - delta - epsilon)
> > >> > rN * sin(rho) / sin(delta)
> > >> > )
> > >> >
> > >> > [rx * cos(phi), rx * sin(phi)]
> > >> > ];
> > >> >
> > >> > // quick and dirty prototype for testing
> > >> > minkowski() {
> > >> > sphere(2, $fn = 36);
> > >> >
> > >> > difference() {
> > >> > translate([0, 0, -30]) sphere(d = 99, $fn = 120);
> > >> >
> > >> > difference () {
> > >> > translate([0, 0, -35]) cube(110, center = true);
> > >> >
> > >> > linear_extrude(20) polygon(points);
> > >> > }
> > >> > }
> > >> > }
> > >> > _______________________________________________
> > >> > OpenSCAD mailing list
> > >> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > >>
> > >> _______________________________________________
> > >> OpenSCAD mailing list
> > >> To unsubscribe send an email to discuss-leave@lists.openscad.org
> > >>
> > > _______________________________________________
> > > OpenSCAD mailing list
> > > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > > _______________________________________________
> > > OpenSCAD mailing list
> > > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
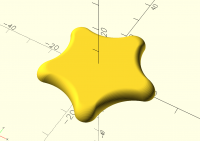

RW
Raymond West
Thu, Dec 26, 2024 9:16 PM
It's the rounding of edges where layer lines will show, or where
overhangs are too great. A bevel works far better in those cases, at any
size. Having to remember to set adaptive in the slicer, and the fun an
games if the roundings are at different layers, is not something I want
to do too often. I do not notice much difference in rounding over the
top of say a 3mm wide strip, compared to bevelling it, and bevels are
easier to create, at least for me. but, I'm mainly concerned with
functional prints, use a 0.6mm nozzle, print as fast as I can, with
thick layer lines.
This largish replica of a cast iron bearing cap, has a smooth curved top
surface. However, it printed flawlessly on it's side, with just a few
supports for the holes (which were oversized for the one inch bolts),
and most of the bottom (side in this view). Printing it 'right way up'
would have given a right messy result at the part that you would
immediately see. Printing with 'fuzzy skin' can also be helpful to hide
layer lines, but slows the process down.
On 26/12/2024 19:06, Adrian Mariano via Discuss wrote:
Ray, are you saying it's only the upside-down rounded edges that you
think are "awful"? I don't really understand. I basically round
every edge I possibly can in my models---but that doesn't include
upside-down ones. I'll have to look into that adaptive layer thickness.
On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss
discuss@lists.openscad.org wrote:
On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
I'm not sure what Ray has against rounded edges. I use them all
the time and think they look and feel great in my FDM printed
models.
What does NOT look great in my experience is something like the
gradual dome top of the knob, which tends to have a very exposed
layer line step-structure with very wide and visible steps that I
think look and feel pretty bad. That will be worse the closer
you are to flat---I don't know how bad it would look with the
model as shown. I printed a knob to go on my audio amp and my
first version had a domed top like shown and I scratched that and
went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed
upside down.
Hi Adrian, you half answered your own question to me, and nop head
gave the top half answer, wrt adaptive.
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
It's the rounding of edges where layer lines will show, or where
overhangs are too great. A bevel works far better in those cases, at any
size. Having to remember to set adaptive in the slicer, and the fun an
games if the roundings are at different layers, is not something I want
to do too often. I do not notice much difference in rounding over the
top of say a 3mm wide strip, compared to bevelling it, and bevels are
easier to create, at least for me. but, I'm mainly concerned with
functional prints, use a 0.6mm nozzle, print as fast as I can, with
thick layer lines.
This largish replica of a cast iron bearing cap, has a smooth curved top
surface. However, it printed flawlessly on it's side, with just a few
supports for the holes (which were oversized for the one inch bolts),
and most of the bottom (side in this view). Printing it 'right way up'
would have given a right messy result at the part that you would
immediately see. Printing with 'fuzzy skin' can also be helpful to hide
layer lines, but slows the process down.
On 26/12/2024 19:06, Adrian Mariano via Discuss wrote:
> Ray, are you saying it's only the upside-down rounded edges that you
> think are "awful"? I don't really understand. I basically round
> every edge I possibly can in my models---but that doesn't include
> upside-down ones. I'll have to look into that adaptive layer thickness.
>
> On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss
> <discuss@lists.openscad.org> wrote:
>
>
> On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
>> I'm not sure what Ray has against rounded edges. I use them all
>> the time and think they look and feel great in my FDM printed
>> models.
>>
>> What does NOT look great in my experience is something like the
>> gradual dome top of the knob, which tends to have a very exposed
>> layer line step-structure with very wide and visible steps that I
>> think look and feel pretty bad. That will be worse the closer
>> you are to flat---I don't know how bad it would look with the
>> model as shown. I printed a knob to go on my audio amp and my
>> first version had a domed top like shown and I scratched that and
>> went back to flat after I felt the model in hand.
>>
>> The other thing that does NOT look great is a roundover printed
>> upside down.
>>
> Hi Adrian, you half answered your own question to me, and nop head
> gave the top half answer, wrt adaptive.
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email todiscuss-leave@lists.openscad.org


RW
Raymond West
Fri, Dec 27, 2024 4:29 PM
Although I have no requirement, having done similar before, Thomas's
original post and other comments has dragged me again into the rabbit
hole of 'scalloped knobs'. Basically, it is a disc, with circles added
around the circumference and other circles subtracted, giving a sort of
sine wave around the circumference. If both sets of circles are the same
size, then it will simplify the code. I drew something out in openscad,
and then thought, 'why stick with 5 scallops?', so I decided to go for
any number between 3 and 9 inclusive.
By eyeballing the location of the circles, it was pretty obvious there
was some sort of geometric formula between the relationship of the
various diameters and positions. Basically straight forward Pythagoras,
but there are quite a few triangles involved. Anyway, it was relatively
quick to eyeball the values.
Having done that, I asked ChatGPT to generate the graphs and calculate
the formula, based on my eyeballed values. The code becomes much more
succinct, and the result is good enough for all practical purposes. It
falls apart for more than nine or ten scallops, but I'm pretty sure that
a few extra values, say for 30, 40 would improve the accuracy.
If it is any use to anyone, or of the slightest interest, I've attached
the script, including my commented eyeballed values, which in some
instances is better than the calculated (the values for md were more
difficult to for me to see, so errors will skew the graph). In the
script, the 'diameter' is approxi'mate, you only need to alter that and
the value for 's'. (if you add 0.7 to the integer value for s, you also
get a sort of index pointer😉)
Although I have no requirement, having done similar before, Thomas's
original post and other comments has dragged me again into the rabbit
hole of 'scalloped knobs'. Basically, it is a disc, with circles added
around the circumference and other circles subtracted, giving a sort of
sine wave around the circumference. If both sets of circles are the same
size, then it will simplify the code. I drew something out in openscad,
and then thought, 'why stick with 5 scallops?', so I decided to go for
any number between 3 and 9 inclusive.
By eyeballing the location of the circles, it was pretty obvious there
was some sort of geometric formula between the relationship of the
various diameters and positions. Basically straight forward Pythagoras,
but there are quite a few triangles involved. Anyway, it was relatively
quick to eyeball the values.
Having done that, I asked ChatGPT to generate the graphs and calculate
the formula, based on my eyeballed values. The code becomes much more
succinct, and the result is good enough for all practical purposes. It
falls apart for more than nine or ten scallops, but I'm pretty sure that
a few extra values, say for 30, 40 would improve the accuracy.
If it is any use to anyone, or of the slightest interest, I've attached
the script, including my commented eyeballed values, which in some
instances is better than the calculated (the values for md were more
difficult to for me to see, so errors will skew the graph). In the
script, the 'diameter' is approxi'mate, you only need to alter that and
the value for 's'. (if you add 0.7 to the integer value for s, you also
get a sort of index pointer😉)

RW
Raymond West
Mon, Dec 30, 2024 6:14 PM
The image shows the diameters for various circles involved in producing
scalloped circles. I gave up in trying to generate a simple formula, as
such, and have derived the values from basic geometry. It was easiest to
view that in line drawings, so I wrote some generic modules to create
lines and basic outline shapes in openscad script. Having done that I
was able to create 2d line drawings, which made it easier to see the
relationship between the various components.
The result I achieved, works for any number of scallops, above one, up
to the limits of floating point calculations, I guess.
The image shows the construction lines and needed dimensions for five
scalloped circles, the only values need to generate them is the number
of scallops, and the diameter of the scallops. The concentric circles
are those needed for generating the shape. The thicker line represents
the base circle. There will then be a number of circles of the same
diameter as the scallop diameter placed with their centres on the inner
circle, and unioned to that base circle There are also circles placed on
the circumference of the outer circle, and differenced. That gives a
circle with a scalloped edge, with smooth transitions. The third circle,
from the centre, is the 'diameter' of the final shape.
>
The image shows the diameters for various circles involved in producing
scalloped circles. I gave up in trying to generate a simple formula, as
such, and have derived the values from basic geometry. It was easiest to
view that in line drawings, so I wrote some generic modules to create
lines and basic outline shapes in openscad script. Having done that I
was able to create 2d line drawings, which made it easier to see the
relationship between the various components.
The result I achieved, works for any number of scallops, above one, up
to the limits of floating point calculations, I guess.
The image shows the construction lines and needed dimensions for five
scalloped circles, the only values need to generate them is the number
of scallops, and the diameter of the scallops. The concentric circles
are those needed for generating the shape. The thicker line represents
the base circle. There will then be a number of circles of the same
diameter as the scallop diameter placed with their centres on the inner
circle, and unioned to that base circle There are also circles placed on
the circumference of the outer circle, and differenced. That gives a
circle with a scalloped edge, with smooth transitions. The third circle,
from the centre, is the 'diameter' of the final shape.
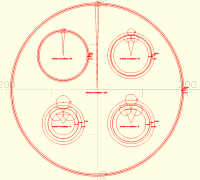

TR
Thomas Richter
Sun, Jan 5, 2025 9:45 PM
Hi all,
I wish you all a good start into the new year.
I took a few days off and worked on it only sporadically but today I finished the analytical solution (almost - see problem description below). The base body can be created in the current state of the software. The object in the images attached here renders in about 500 milliseconds.
It can be found here: https://github.com/trses/screw-nut-knobs/blob/webapp-proto/analytical-solution.scad
@Raymond: I am convinced that there is not one (rather simple trigonometric) formula that can generate the shape, but two for the two different arcs. You also have to determine the points of contact of the two arcs. It can of course probably be solved with a Taylor-like approximation but I didn't want to go that way.
This afternoon I realised that I'm almost done building a general solution to make any polyhedron out of an arbitrary list of layers of points. They points of one layer can even have different z values. I might go those few final steps sometimes but at next I will build the web application to generate the knobs.
If anyone has the nerve to look at this, I'd be interested in suggestions on how the features of OpenSCAD could be better utilised. I have a very software engineering heavy approach to tackling these things.
Additionally, I realized a strange problem: when setting the number of arms (variable ARMS) to 13 or 17 the following error occurs:
WARNING: PolySet -> Manifold conversion failed: NotManifold
Trying to repair and reconstruct mesh..
ERROR: [manifold] Input mesh is not closed!
ERROR: [manifold] Surface_mesh -> Manifold conversion failed: NotManifold
There are a couple more value combinations where this happens but there seems to be no general rule. For larger numbers of arms like - e. g. - 20 it works again. If you comment out the subtraction of the hollow sphere in line 147 it renders without problems (but looks strange though ;-)). I have checked the polyhedron several times by hand, it is generated correctly.
OpenSCAD seems to have a glitch with boolean operations on more sophisticated shapes, possibly especially when there seem to be very small resulting faces.
It would be nice if someone had an idea about this. I could easily extend the body and generate additional layers for the surface to omit the subtraction at all but I'd like to understand what's the cause.
Thanks again for your support.
Am 26.12.2024 um 20:06 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
Ray, are you saying it's only the upside-down rounded edges that you think are "awful"? I don't really understand. I basically round every edge I possibly can in my models---but that doesn't include upside-down ones. I'll have to look into that adaptive layer thickness.
On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss discuss@lists.openscad.org wrote:
On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside down.
Hi all,
I wish you all a good start into the new year.
I took a few days off and worked on it only sporadically but today I finished the analytical solution (almost - see problem description below). The base body can be created in the current state of the software. The object in the images attached here renders in about 500 milliseconds.
It can be found here: https://github.com/trses/screw-nut-knobs/blob/webapp-proto/analytical-solution.scad
@Raymond: I am convinced that there is not one (rather simple trigonometric) formula that can generate the shape, but two for the two different arcs. You also have to determine the points of contact of the two arcs. It can of course probably be solved with a Taylor-like approximation but I didn't want to go that way.
This afternoon I realised that I'm almost done building a general solution to make any polyhedron out of an arbitrary list of layers of points. They points of one layer can even have different z values. I might go those few final steps sometimes but at next I will build the web application to generate the knobs.
If anyone has the nerve to look at this, I'd be interested in suggestions on how the features of OpenSCAD could be better utilised. I have a very software engineering heavy approach to tackling these things.
Additionally, I realized a strange problem: when setting the number of arms (variable ARMS) to 13 or 17 the following error occurs:
WARNING: PolySet -> Manifold conversion failed: NotManifold
Trying to repair and reconstruct mesh..
ERROR: [manifold] Input mesh is not closed!
ERROR: [manifold] Surface_mesh -> Manifold conversion failed: NotManifold
There are a couple more value combinations where this happens but there seems to be no general rule. For larger numbers of arms like - e. g. - 20 it works again. If you comment out the subtraction of the hollow sphere in line 147 it renders without problems (but looks strange though ;-)). I have checked the polyhedron several times by hand, it is generated correctly.
OpenSCAD seems to have a glitch with boolean operations on more sophisticated shapes, possibly especially when there seem to be very small resulting faces.
It would be nice if someone had an idea about this. I could easily extend the body and generate additional layers for the surface to omit the subtraction at all but I'd like to understand what's the cause.
Thanks again for your support.
> Am 26.12.2024 um 20:06 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
>
> Ray, are you saying it's only the upside-down rounded edges that you think are "awful"? I don't really understand. I basically round every edge I possibly can in my models---but that doesn't include upside-down ones. I'll have to look into that adaptive layer thickness.
>
> On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss <discuss@lists.openscad.org> wrote:
>
> On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
>> I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
>>
>> What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
>>
>> The other thing that does NOT look great is a roundover printed upside down.
>>
> Hi Adrian, you half answered your own question to me, and nop head gave the top half answer, wrt adaptive.
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
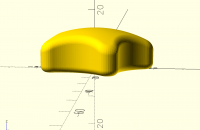

RW
Raymond West
Mon, Jan 6, 2025 1:03 AM
There is a formula, but a bit tricky, as I said, a number of triangles
involved. The 2d line drawing I posted a few days ago gave an indication
of the construction of the basic shape. I completed it for the simple
case, where the scallop diameter equals the diameter of the 'blobs'
lying between them.
There are only four parameters required for the basic shape, for example
- calculate(s=5,knob=48,fil=6,thick=15) (s is number of scallops, knob
is overall diameter, fil is radius of fillet (top and bottom), thick is
total thickness.) It works fine now, from one scallop up to whatever. (I
argued with myself wrt one scallop, whether or not it should produce no
knob, but I settled on a simple circular one - if the scallop size was
smaller, then there would be no argument 🙂).
The more scallops, or the larger the knob, the slower the Minkowski. I
modified my bevel script, to do round-overs, I think that would be
quicker, than Minkowski, but would depend on the radius of the
round-overs. (The above values for 'calculate' takes less than ten
seconds to calculate using manifold, and 25 seconds for 25 scallops,
both using Minkowski.)
If there are different radii for the scallops compared to the 'blobs',
then the triangles between the centres are no longer equilateral, but
Isosceles, which makes the calculations a bit different, but not much
more so, I've not bothered with that, although it would be the generic
formula, it would introduce a couple more more parameters, unnecessary
choices when none need to made if all we are concerned with are generic
scalloped knobs for fdm printing.
On 05/01/2025 21:45, Thomas Richter via Discuss wrote:
Hi all,
I wish you all a good start into the new year.
I took a few days off and worked on it only sporadically but today I finished the analytical solution (almost - see problem description below). The base body can be created in the current state of the software. The object in the images attached here renders in about 500 milliseconds.
It can be found here: https://github.com/trses/screw-nut-knobs/blob/webapp-proto/analytical-solution.scad
@Raymond: I am convinced that there is not one (rather simple trigonometric) formula that can generate the shape, but two for the two different arcs. You also have to determine the points of contact of the two arcs. It can of course probably be solved with a Taylor-like approximation but I didn't want to go that way.
This afternoon I realised that I'm almost done building a general solution to make any polyhedron out of an arbitrary list of layers of points. They points of one layer can even have different z values. I might go those few final steps sometimes but at next I will build the web application to generate the knobs.
If anyone has the nerve to look at this, I'd be interested in suggestions on how the features of OpenSCAD could be better utilised. I have a very software engineering heavy approach to tackling these things.
Additionally, I realized a strange problem: when setting the number of arms (variable ARMS) to 13 or 17 the following error occurs:
WARNING: PolySet -> Manifold conversion failed: NotManifold
Trying to repair and reconstruct mesh..
ERROR: [manifold] Input mesh is not closed!
ERROR: [manifold] Surface_mesh -> Manifold conversion failed: NotManifold
There are a couple more value combinations where this happens but there seems to be no general rule. For larger numbers of arms like - e. g. - 20 it works again. If you comment out the subtraction of the hollow sphere in line 147 it renders without problems (but looks strange though ;-)). I have checked the polyhedron several times by hand, it is generated correctly.
OpenSCAD seems to have a glitch with boolean operations on more sophisticated shapes, possibly especially when there seem to be very small resulting faces.
It would be nice if someone had an idea about this. I could easily extend the body and generate additional layers for the surface to omit the subtraction at all but I'd like to understand what's the cause.
Thanks again for your support.
Am 26.12.2024 um 20:06 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
Ray, are you saying it's only the upside-down rounded edges that you think are "awful"? I don't really understand. I basically round every edge I possibly can in my models---but that doesn't include upside-down ones. I'll have to look into that adaptive layer thickness.
On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss discuss@lists.openscad.org wrote:
On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
The other thing that does NOT look great is a roundover printed upside down.
Hi Adrian, you half answered your own question to me, and nop head gave the top half answer, wrt adaptive.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
There is a formula, but a bit tricky, as I said, a number of triangles
involved. The 2d line drawing I posted a few days ago gave an indication
of the construction of the basic shape. I completed it for the simple
case, where the scallop diameter equals the diameter of the 'blobs'
lying between them.
There are only four parameters required for the basic shape, for example
- calculate(s=5,knob=48,fil=6,thick=15) (s is number of scallops, knob
is overall diameter, fil is radius of fillet (top and bottom), thick is
total thickness.) It works fine now, from one scallop up to whatever. (I
argued with myself wrt one scallop, whether or not it should produce no
knob, but I settled on a simple circular one - if the scallop size was
smaller, then there would be no argument 🙂).
The more scallops, or the larger the knob, the slower the Minkowski. I
modified my bevel script, to do round-overs, I think that would be
quicker, than Minkowski, but would depend on the radius of the
round-overs. (The above values for 'calculate' takes less than ten
seconds to calculate using manifold, and 25 seconds for 25 scallops,
both using Minkowski.)
If there are different radii for the scallops compared to the 'blobs',
then the triangles between the centres are no longer equilateral, but
Isosceles, which makes the calculations a bit different, but not much
more so, I've not bothered with that, although it would be the generic
formula, it would introduce a couple more more parameters, unnecessary
choices when none need to made if all we are concerned with are generic
scalloped knobs for fdm printing.
On 05/01/2025 21:45, Thomas Richter via Discuss wrote:
> Hi all,
>
> I wish you all a good start into the new year.
>
> I took a few days off and worked on it only sporadically but today I finished the analytical solution (almost - see problem description below). The base body can be created in the current state of the software. The object in the images attached here renders in about 500 milliseconds.
>
> It can be found here: https://github.com/trses/screw-nut-knobs/blob/webapp-proto/analytical-solution.scad
>
> @Raymond: I am convinced that there is not one (rather simple trigonometric) formula that can generate the shape, but two for the two different arcs. You also have to determine the points of contact of the two arcs. It can of course probably be solved with a Taylor-like approximation but I didn't want to go that way.
>
> This afternoon I realised that I'm almost done building a general solution to make any polyhedron out of an arbitrary list of layers of points. They points of one layer can even have different z values. I might go those few final steps sometimes but at next I will build the web application to generate the knobs.
>
> If anyone has the nerve to look at this, I'd be interested in suggestions on how the features of OpenSCAD could be better utilised. I have a very software engineering heavy approach to tackling these things.
>
> Additionally, I realized a strange problem: when setting the number of arms (variable ARMS) to 13 or 17 the following error occurs:
>
> WARNING: PolySet -> Manifold conversion failed: NotManifold
> Trying to repair and reconstruct mesh..
> ERROR: [manifold] Input mesh is not closed!
> ERROR: [manifold] Surface_mesh -> Manifold conversion failed: NotManifold
>
> There are a couple more value combinations where this happens but there seems to be no general rule. For larger numbers of arms like - e. g. - 20 it works again. If you comment out the subtraction of the hollow sphere in line 147 it renders without problems (but looks strange though ;-)). I have checked the polyhedron several times by hand, it is generated correctly.
>
> OpenSCAD seems to have a glitch with boolean operations on more sophisticated shapes, possibly especially when there seem to be very small resulting faces.
>
> It would be nice if someone had an idea about this. I could easily extend the body and generate additional layers for the surface to omit the subtraction at all but I'd like to understand what's the cause.
>
> Thanks again for your support.
>
>> Am 26.12.2024 um 20:06 schrieb Adrian Mariano via Discuss <discuss@lists.openscad.org>:
>>
>> Ray, are you saying it's only the upside-down rounded edges that you think are "awful"? I don't really understand. I basically round every edge I possibly can in my models---but that doesn't include upside-down ones. I'll have to look into that adaptive layer thickness.
>>
>> On Thu, Dec 26, 2024 at 2:00 PM Raymond West via Discuss <discuss@lists.openscad.org> wrote:
>>
>> On 26/12/2024 15:03, Adrian Mariano via Discuss wrote:
>>> I'm not sure what Ray has against rounded edges. I use them all the time and think they look and feel great in my FDM printed models.
>>>
>>> What does NOT look great in my experience is something like the gradual dome top of the knob, which tends to have a very exposed layer line step-structure with very wide and visible steps that I think look and feel pretty bad. That will be worse the closer you are to flat---I don't know how bad it would look with the model as shown. I printed a knob to go on my audio amp and my first version had a domed top like shown and I scratched that and went back to flat after I felt the model in hand.
>>>
>>> The other thing that does NOT look great is a roundover printed upside down.
>>>
>> Hi Adrian, you half answered your own question to me, and nop head gave the top half answer, wrt adaptive.
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org






