BA
Brian Allen
Tue, Aug 2, 2022 11:46 PM
Hi,
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
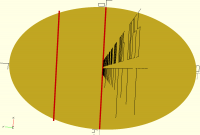
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
Any ideas?
Thanks,
Brian
Hi,
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
Any ideas?
Thanks,
Brian

JB
Jordan Brown
Wed, Aug 3, 2022 12:04 AM
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3*u*(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end,
and the end point. I have sometimes created OpenSCAD objects by tracing
an object in a drawing program and then reading off the coordinates of
the various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
On 8/2/2022 4:46 PM, Brian Allen wrote:
> I created an oval using:
> inMm = 25.4;
> fullW = 35.5 * inMm;
> fullL = 54.5 * inMm;
> resize([fullW, fullL, 1])
> circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this technique.
> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3*u*(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end,
and the end point. I have sometimes created OpenSCAD objects by tracing
an object in a drawing program and then reading off the coordinates of
the various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.

JB
Jordan Brown
Wed, Aug 3, 2022 12:25 AM
More generally, if you can define a function that returns the values
around your curve, you can use list comprehension to generate a list of
points that you can then feed to polygon().
For instance, here's a sequence that will generate a unit circle:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) = let(a = i*360) [ cos(a), sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Here's a sequence that will generate a race track:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) =
i < 0.125
? let(a = i*2*360) [ cos(a) + 0.5, sin(a) ]
: i < 0.375
? [ (0.25 - i)*4, 1 ]
: i < 0.625
? let(a = (i-0.25)*2*360) [ cos(a) - 0.5, sin(a) ]
: i < 0.875
? [ (i - 0.75)*4, -1 ]
: let(a = (i-1)*2*360) [ cos(a) + 0.5, sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Not that there aren't easier ways to do both of those (circle, hull of
two circles), but the technique is general: it will work for any shape
that you can represent as a function of [0..1].
More generally, if you can define a function that returns the values
around your curve, you can use list comprehension to generate a list of
points that you can then feed to polygon().
For instance, here's a sequence that will generate a unit circle:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) = let(a = i*360) [ cos(a), sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Here's a sequence that will generate a race track:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) =
i < 0.125
? let(a = i*2*360) [ cos(a) + 0.5, sin(a) ]
: i < 0.375
? [ (0.25 - i)*4, 1 ]
: i < 0.625
? let(a = (i-0.25)*2*360) [ cos(a) - 0.5, sin(a) ]
: i < 0.875
? [ (i - 0.75)*4, -1 ]
: let(a = (i-1)*2*360) [ cos(a) + 0.5, sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Not that there aren't easier ways to do both of those (circle, hull of
two circles), but the technique is general: it will work for any shape
that you can represent as a function of [0..1].

MM
Michael Marx
Wed, Aug 3, 2022 12:45 AM
Or old school.
Scan the shape to PNG, load it via surface(). Or DXF/SVG via import().
Or
Plot your points on graph paper, for the top half of the curve.
Put the values in an array, calculate the negative side, make a polygon.
From: Jordan Brown [mailto:openscad@jordan.maileater.net]
Sent: Wed, 3 Aug 2022 10:26
To: OpenSCAD general discussion; Brian Allen
Subject: [OpenSCAD] Re: Transforming an Oval
More generally, if you can define a function that returns the values around your curve, you can use list comprehension to generate a list of points that you can then feed to polygon().
For instance, here's a sequence that will generate a unit circle:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) = let(a = i*360) [ cos(a), sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Here's a sequence that will generate a race track:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) =
i < 0.125
? let(a = i2360) [ cos(a) + 0.5, sin(a) ]
: i < 0.375
? [ (0.25 - i)*4, 1 ]
: i < 0.625
? let(a = (i-0.25)2360) [ cos(a) - 0.5, sin(a) ]
: i < 0.875
? [ (i - 0.75)*4, -1 ]
: let(a = (i-1)2360) [ cos(a) + 0.5, sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Not that there aren't easier ways to do both of those (circle, hull of two circles), but the technique is general: it will work for any shape that you can represent as a function of [0..1].
--
This email has been checked for viruses by AVG.
https://www.avg.com
Or old school.
Scan the shape to PNG, load it via surface(). Or DXF/SVG via import().
Or
Plot your points on graph paper, for the top half of the curve.
Put the values in an array, calculate the negative side, make a polygon.
_____
From: Jordan Brown [mailto:openscad@jordan.maileater.net]
Sent: Wed, 3 Aug 2022 10:26
To: OpenSCAD general discussion; Brian Allen
Subject: [OpenSCAD] Re: Transforming an Oval
More generally, if you can define a function that returns the values around your curve, you can use list comprehension to generate a list of points that you can then feed to polygon().
For instance, here's a sequence that will generate a unit circle:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) = let(a = i*360) [ cos(a), sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Here's a sequence that will generate a race track:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) =
i < 0.125
? let(a = i*2*360) [ cos(a) + 0.5, sin(a) ]
: i < 0.375
? [ (0.25 - i)*4, 1 ]
: i < 0.625
? let(a = (i-0.25)*2*360) [ cos(a) - 0.5, sin(a) ]
: i < 0.875
? [ (i - 0.75)*4, -1 ]
: let(a = (i-1)*2*360) [ cos(a) + 0.5, sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Not that there aren't easier ways to do both of those (circle, hull of two circles), but the technique is general: it will work for any shape that you can represent as a function of [0..1].
--
This email has been checked for viruses by AVG.
https://www.avg.com

BA
Brian Allen
Wed, Aug 3, 2022 1:19 AM
Thank you both. I really appreciate it. One of those solutions will work for my needs, I'm sure.
Brian
On Tue, Aug 2, 2022, at 6:45 PM, Michael Marx wrote:
Or old school.
Scan the shape to PNG, load it via surface(). Or DXF/SVG via import().
Or
Plot your points on graph paper, for the top half of the curve.
Put the values in an array, calculate the negative side, make a polygon.
From: Jordan Brown [mailto:openscad@jordan.maileater.net]
Sent: Wed, 3 Aug 2022 10:26
To: OpenSCAD general discussion; Brian Allen
Subject: [OpenSCAD] Re: Transforming an Oval
More generally, if you can define a function that returns the values around your curve, you can use list comprehension to generate a list of points that you can then feed to polygon().
For instance, here's a sequence that will generate a unit circle:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) = let(a = i*360) [ cos(a), sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Here's a sequence that will generate a race track:
// Define f to be a function that accepts a value between 0 and 1
// and returns a corresponding coordinate.
function f(i) =
i < 0.125
? let(a = i2360) [ cos(a) + 0.5, sin(a) ]
: i < 0.375
? [ (0.25 - i)*4, 1 ]
: i < 0.625
? let(a = (i-0.25)2360) [ cos(a) - 0.5, sin(a) ]
: i < 0.875
? [ (i - 0.75)*4, -1 ]
: let(a = (i-1)2360) [ cos(a) + 0.5, sin(a) ];
points = [ for (i = [0:0.01:1]) f(i) ];
polygon(points);
Not that there aren't easier ways to do both of those (circle, hull of two circles), but the technique is general: it will work for any shape that you can represent as a function of [0..1].
Thank you both. I really appreciate it. One of those solutions will work for my needs, I'm sure.
Brian
On Tue, Aug 2, 2022, at 6:45 PM, Michael Marx wrote:
> Or old school.
>
> Scan the shape to PNG, load it via surface(). Or DXF/SVG via import().
> Or
> Plot your points on graph paper, for the top half of the curve.
> Put the values in an array, calculate the negative side, make a polygon.
>
>
> **From:** Jordan Brown [mailto:openscad@jordan.maileater.net]
> **Sent:** Wed, 3 Aug 2022 10:26
> **To:** OpenSCAD general discussion; Brian Allen
> **Subject:** [OpenSCAD] Re: Transforming an Oval
>
> More generally, if you can define a function that returns the values around your curve, you can use list comprehension to generate a list of points that you can then feed to polygon().
>
> For instance, here's a sequence that will generate a unit circle:
> // Define f to be a function that accepts a value between 0 and 1
> // and returns a corresponding coordinate.
> function f(i) = let(a = i*360) [ cos(a), sin(a) ];
>
> points = [ for (i = [0:0.01:1]) f(i) ];
> polygon(points);
> Here's a sequence that will generate a race track:
> // Define f to be a function that accepts a value between 0 and 1
> // and returns a corresponding coordinate.
> function f(i) =
> i < 0.125
> ? let(a = i*2*360) [ cos(a) + 0.5, sin(a) ]
> : i < 0.375
> ? [ (0.25 - i)*4, 1 ]
> : i < 0.625
> ? let(a = (i-0.25)*2*360) [ cos(a) - 0.5, sin(a) ]
> : i < 0.875
> ? [ (i - 0.75)*4, -1 ]
> : let(a = (i-1)*2*360) [ cos(a) + 0.5, sin(a) ];
>
> points = [ for (i = [0:0.01:1]) f(i) ];
> polygon(points);
> Not that there aren't easier ways to do both of those (circle, hull of two circles), but the technique is general: it will work for any shape that you can represent as a function of [0..1].
>
>
>
<http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient>
> Virus-free. www.avg.com <http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient>
<https://www.fastmail.com/mail/Inbox/compose?u=00a140e7#DAB4FAD8-2DD7-40BB-A1B8-4E2AA1F9FDF2>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Wed, Aug 3, 2022 2:35 AM
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, openscad@jordan.maileater.net
wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in complicated
cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching is
an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in - but
I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically flow
from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net>
wrote:
> On 8/2/2022 4:46 PM, Brian Allen wrote:
>
> I created an oval using:
> inMm = 25.4;
> fullW = 35.5 * inMm;
> fullL = 54.5 * inMm;
> resize([fullW, fullL, 1])
> circle(d=fullW);
>
>
> Tip: use scale() rather than resize(); it previews faster in complicated
> cases.
>
> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>
>
> You're taking a circle and stretching it; the result of that stretching is
> an ellipse.
>
> I'm not 100% sure - maybe one of the real math wizards can chime in - but
> I think the shape you are asking for would not be an ellipse.
>
> I believe that an ellipse is fully defined by its major (long) and minor
> (short) axis dimensions; the other parts of the curve mathematically flow
> from those two measurements.
>
> You can make something else, but you can't make it using this technique.
>
> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>
>
> You can use a Bézier function.
>
> Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>
> DIY, here's a function that I cobbled together some years ago:
>
> // Bezier functions from https://www.thingiverse.com/thing:8443
> // but that yielded either single points or a raft of triangles;
> // this yields a vector of points that you can then concatenate
> // with other pieces to form a single polygon.
> // If we were really clever, I think it would be possible to
> // automatically space the output points based on how linear
> // the curve is at that point. But right now I'm not that clever.
> function BEZ03(u) = pow((1-u), 3);
> function BEZ13(u) = 3*u*(pow((1-u),2));
> function BEZ23(u) = 3*(pow(u,2))*(1-u);
> function BEZ33(u) = pow(u,3);
>
> function PointAlongBez4(p0, p1, p2, p3, u) = [
> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>
> // p0 - start point
> // p1 - control point 1, line departs p0 headed this way
> // p2 - control point 2, line arrives at p3 from this way
> // p3 - end point
> // segs - number of segments
> function bez(p0, p1, p2, p3, segs) = [
> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
> ];
>
> It is that final function bez() that I actually call, e.g.
>
> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>
> often concatenating the results of several bez() calls together.
>
> Note that the four coordinates correspond to the coordinates of the
> control points in a GUI drawing program: the start point, control point
> associated with the start, the control point associated with the end, and
> the end point. I have sometimes created OpenSCAD objects by tracing an
> object in a drawing program and then reading off the coordinates of the
> various control points.
>
>
> Note that Bézier functions are not the only mathematical curves. (For
> instance, they cannot exactly match an arc of a circle.) I'm sure there
> are numerous other functions that also produce curves.
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Wed, Aug 3, 2022 2:50 AM
Here's a challenge for you: draw an "ellipse" polygon with N segments that
are all the same length that circumscribes a perfect ellipse with given
semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, openscad@jordan.maileater.net
wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in complicated
cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in - but
I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically flow
from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Here's a challenge for you: draw an "ellipse" polygon with N segments that
are all the same length that circumscribes a perfect ellipse with given
semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an *inscribed* N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> In openscad drawing a ellipse is not too difficult
> Refer following code
>
> function to draw an ellipse with semi-major and semi-minor axis "r1" and
> "r2" respectively and with center "cp" and number of segment "s"
> /
> // example:
> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>
> function ellipse(r1,r2,cp,s=30)=
> let(
> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
> )sec;
>
> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net>
> wrote:
>
>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>
>> I created an oval using:
>> inMm = 25.4;
>> fullW = 35.5 * inMm;
>> fullL = 54.5 * inMm;
>> resize([fullW, fullL, 1])
>> circle(d=fullW);
>>
>>
>> Tip: use scale() rather than resize(); it previews faster in complicated
>> cases.
>>
>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>
>>
>> You're taking a circle and stretching it; the result of that stretching
>> is an ellipse.
>>
>> I'm not 100% sure - maybe one of the real math wizards can chime in - but
>> I think the shape you are asking for would not be an ellipse.
>>
>> I believe that an ellipse is fully defined by its major (long) and minor
>> (short) axis dimensions; the other parts of the curve mathematically flow
>> from those two measurements.
>>
>> You can make something else, but you can't make it using this technique.
>>
>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>
>>
>> You can use a Bézier function.
>>
>> Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>
>> DIY, here's a function that I cobbled together some years ago:
>>
>> // Bezier functions from https://www.thingiverse.com/thing:8443
>> // but that yielded either single points or a raft of triangles;
>> // this yields a vector of points that you can then concatenate
>> // with other pieces to form a single polygon.
>> // If we were really clever, I think it would be possible to
>> // automatically space the output points based on how linear
>> // the curve is at that point. But right now I'm not that clever.
>> function BEZ03(u) = pow((1-u), 3);
>> function BEZ13(u) = 3*u*(pow((1-u),2));
>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>> function BEZ33(u) = pow(u,3);
>>
>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>
>> // p0 - start point
>> // p1 - control point 1, line departs p0 headed this way
>> // p2 - control point 2, line arrives at p3 from this way
>> // p3 - end point
>> // segs - number of segments
>> function bez(p0, p1, p2, p3, segs) = [
>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>> ];
>>
>> It is that final function bez() that I actually call, e.g.
>>
>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>
>> often concatenating the results of several bez() calls together.
>>
>> Note that the four coordinates correspond to the coordinates of the
>> control points in a GUI drawing program: the start point, control point
>> associated with the start, the control point associated with the end, and
>> the end point. I have sometimes created OpenSCAD objects by tracing an
>> object in a drawing program and then reading off the coordinates of the
>> various control points.
>>
>>
>> Note that Bézier functions are not the only mathematical curves. (For
>> instance, they cannot exactly match an arc of a circle.) I'm sure there
>> are numerous other functions that also produce curves.
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

GH
gene heskett
Wed, Aug 3, 2022 2:53 AM
On 8/2/22 19:50, Brian Allen wrote:
Hi,
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
Any ideas?
Thanks,
Brian
I'm not sure if it would meet your needs, but I made the elliptical
armature for a 50/1 harmonic drive by
using the scale module on a cylinder, then scaling it 1.05 in the x
direction, and .95 in the y direction.
It worked pretty good and printed in PETG lasted well too, but given the
motors to drive it, and
the heat in the flexible bearings I also printed, it was too slow to do
what I wanted to do. So I
bought a 5/1 worm, put a 3NM 3 phase motor on it and I was off to the
races. Its the B drive
on my 6040 milling machine.
Cheers, Gene Heskett.
"There are four boxes to be used in defense of liberty:
soap, ballot, jury, and ammo. Please use in that order."
-Ed Howdershelt (Author, 1940)
If we desire respect for the law, we must first make the law respectable.
On 8/2/22 19:50, Brian Allen wrote:
> Hi,
>
> I created an oval using:
> inMm = 25.4;
> fullW = 35.5 * inMm;
> fullL = 54.5 * inMm;
> resize([fullW, fullL, 1])
> circle(d=fullW);
>
> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>
> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>
> Any ideas?
>
> Thanks,
> Brian
> I'm not sure if it would meet your needs, but I made the elliptical
> armature for a 50/1 harmonic drive by
using the scale module on a cylinder, then scaling it 1.05 in the x
direction, and .95 in the y direction.
It worked pretty good and printed in PETG lasted well too, but given the
motors to drive it, and
the heat in the flexible bearings I also printed, it was too slow to do
what I wanted to do. So I
bought a 5/1 worm, put a 3NM 3 phase motor on it and I was off to the
races. Its the B drive
on my 6040 milling machine.
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
Cheers, Gene Heskett.
--
"There are four boxes to be used in defense of liberty:
soap, ballot, jury, and ammo. Please use in that order."
-Ed Howdershelt (Author, 1940)
If we desire respect for the law, we must first make the law respectable.
- Louis D. Brandeis
Genes Web page <http://geneslinuxbox.net:6309/>

FH
Father Horton
Wed, Aug 3, 2022 2:55 AM
Except by brute force (step through it with sufficiently small steps), it’s
not possible because there’s no closed form expression for the distance
between two points on a general ellipse (as opposed to special cases like a
circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, openscad@jordan.maileater.net
wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically flow
from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Except by brute force (step through it with sufficiently small steps), it’s
not possible because there’s no closed form expression for the distance
between two points on a general ellipse (as opposed to special cases like a
circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu> wrote:
> Here's a challenge for you: draw an "ellipse" polygon with N segments
> that are all the same length that circumscribes a perfect ellipse with
> given semiaxes a and b. I tried to solve this problem and could not find a
> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
> segments the same length---though it's not easy---but the circumscribed
> case eludes me. I think of the inscribed case as, every vertex is located
> on the ellipse and the circumscribed case, every segment is tangent to the
> ellipse
>
> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> In openscad drawing a ellipse is not too difficult
>> Refer following code
>>
>> function to draw an ellipse with semi-major and semi-minor axis "r1" and
>> "r2" respectively and with center "cp" and number of segment "s"
>> /
>> // example:
>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>
>> function ellipse(r1,r2,cp,s=30)=
>> let(
>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>> )sec;
>>
>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net>
>> wrote:
>>
>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>
>>> I created an oval using:
>>> inMm = 25.4;
>>> fullW = 35.5 * inMm;
>>> fullL = 54.5 * inMm;
>>> resize([fullW, fullL, 1])
>>> circle(d=fullW);
>>>
>>>
>>> Tip: use scale() rather than resize(); it previews faster in
>>> complicated cases.
>>>
>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>
>>>
>>> You're taking a circle and stretching it; the result of that stretching
>>> is an ellipse.
>>>
>>> I'm not 100% sure - maybe one of the real math wizards can chime in -
>>> but I think the shape you are asking for would not be an ellipse.
>>>
>>> I believe that an ellipse is fully defined by its major (long) and minor
>>> (short) axis dimensions; the other parts of the curve mathematically flow
>>> from those two measurements.
>>>
>>> You can make something else, but you can't make it using this technique.
>>>
>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>
>>>
>>> You can use a Bézier function.
>>>
>>> Using BOSL2:
>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>
>>> DIY, here's a function that I cobbled together some years ago:
>>>
>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>> // but that yielded either single points or a raft of triangles;
>>> // this yields a vector of points that you can then concatenate
>>> // with other pieces to form a single polygon.
>>> // If we were really clever, I think it would be possible to
>>> // automatically space the output points based on how linear
>>> // the curve is at that point. But right now I'm not that clever.
>>> function BEZ03(u) = pow((1-u), 3);
>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>> function BEZ33(u) = pow(u,3);
>>>
>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>
>>> // p0 - start point
>>> // p1 - control point 1, line departs p0 headed this way
>>> // p2 - control point 2, line arrives at p3 from this way
>>> // p3 - end point
>>> // segs - number of segments
>>> function bez(p0, p1, p2, p3, segs) = [
>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>> ];
>>>
>>> It is that final function bez() that I actually call, e.g.
>>>
>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>
>>> often concatenating the results of several bez() calls together.
>>>
>>> Note that the four coordinates correspond to the coordinates of the
>>> control points in a GUI drawing program: the start point, control point
>>> associated with the start, the control point associated with the end, and
>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>> object in a drawing program and then reading off the coordinates of the
>>> various control points.
>>>
>>>
>>> Note that Bézier functions are not the only mathematical curves. (For
>>> instance, they cannot exactly match an arc of a circle.) I'm sure there
>>> are numerous other functions that also produce curves.
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Wed, Aug 3, 2022 3:09 AM
Eh, there's no such thing as "brute force" in this situation. Step through
what with sufficiently small steps? Of course an iterative algorithm is
necessary. This is true for most interesting problems. No big deal. Show
me an iterative algorithm that converges to the circumscribing polygon.
When I tried to devise such an algorithm I couldn't find one that would
converge. Writing an algorithm that would converge to the inscribed
polygon seemed to be straight forward. Note also that computing arc
length of the ellipse doesn't really help here. You can do that by solving
an elliptical integral, or summing up small segments. But what's the
connection between arc length of the ellipse and a circumscribing polygon
with equal segment lengths? If there's a connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton fatherhorton@gmail.com
wrote:
Except by brute force (step through it with sufficiently small steps),
it’s not possible because there’s no closed form expression for the
distance between two points on a general ellipse (as opposed to special
cases like a circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and
minor (short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Eh, there's no such thing as "brute force" in this situation. Step through
*what* with sufficiently small steps? Of course an iterative algorithm is
necessary. This is true for most interesting problems. No big deal. Show
me an iterative algorithm that converges to the circumscribing polygon.
When I tried to devise such an algorithm I couldn't find one that would
converge. Writing an algorithm that would converge to the *inscribed*
polygon seemed to be straight forward. Note also that computing arc
length of the ellipse doesn't really help here. You can do that by solving
an elliptical integral, or summing up small segments. But what's the
connection between arc length of the ellipse and a circumscribing polygon
with equal segment lengths? If there's a connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton <fatherhorton@gmail.com>
wrote:
> Except by brute force (step through it with sufficiently small steps),
> it’s not possible because there’s no closed form expression for the
> distance between two points on a general ellipse (as opposed to special
> cases like a circle).
>
> On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Here's a challenge for you: draw an "ellipse" polygon with N segments
>> that are all the same length that circumscribes a perfect ellipse with
>> given semiaxes a and b. I tried to solve this problem and could not find a
>> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
>> segments the same length---though it's not easy---but the circumscribed
>> case eludes me. I think of the inscribed case as, every vertex is located
>> on the ellipse and the circumscribed case, every segment is tangent to the
>> ellipse
>>
>> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> In openscad drawing a ellipse is not too difficult
>>> Refer following code
>>>
>>> function to draw an ellipse with semi-major and semi-minor axis "r1" and
>>> "r2" respectively and with center "cp" and number of segment "s"
>>> /
>>> // example:
>>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>>
>>> function ellipse(r1,r2,cp,s=30)=
>>> let(
>>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>>> )sec;
>>>
>>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
>>> openscad@jordan.maileater.net> wrote:
>>>
>>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>>
>>>> I created an oval using:
>>>> inMm = 25.4;
>>>> fullW = 35.5 * inMm;
>>>> fullL = 54.5 * inMm;
>>>> resize([fullW, fullL, 1])
>>>> circle(d=fullW);
>>>>
>>>>
>>>> Tip: use scale() rather than resize(); it previews faster in
>>>> complicated cases.
>>>>
>>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>>
>>>>
>>>> You're taking a circle and stretching it; the result of that stretching
>>>> is an ellipse.
>>>>
>>>> I'm not 100% sure - maybe one of the real math wizards can chime in -
>>>> but I think the shape you are asking for would not be an ellipse.
>>>>
>>>> I believe that an ellipse is fully defined by its major (long) and
>>>> minor (short) axis dimensions; the other parts of the curve mathematically
>>>> flow from those two measurements.
>>>>
>>>> You can make something else, but you can't make it using this technique.
>>>>
>>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>>
>>>>
>>>> You can use a Bézier function.
>>>>
>>>> Using BOSL2:
>>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>>
>>>> DIY, here's a function that I cobbled together some years ago:
>>>>
>>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>>> // but that yielded either single points or a raft of triangles;
>>>> // this yields a vector of points that you can then concatenate
>>>> // with other pieces to form a single polygon.
>>>> // If we were really clever, I think it would be possible to
>>>> // automatically space the output points based on how linear
>>>> // the curve is at that point. But right now I'm not that clever.
>>>> function BEZ03(u) = pow((1-u), 3);
>>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>>> function BEZ33(u) = pow(u,3);
>>>>
>>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>>
>>>> // p0 - start point
>>>> // p1 - control point 1, line departs p0 headed this way
>>>> // p2 - control point 2, line arrives at p3 from this way
>>>> // p3 - end point
>>>> // segs - number of segments
>>>> function bez(p0, p1, p2, p3, segs) = [
>>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>>> ];
>>>>
>>>> It is that final function bez() that I actually call, e.g.
>>>>
>>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>>
>>>> often concatenating the results of several bez() calls together.
>>>>
>>>> Note that the four coordinates correspond to the coordinates of the
>>>> control points in a GUI drawing program: the start point, control point
>>>> associated with the start, the control point associated with the end, and
>>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>>> object in a drawing program and then reading off the coordinates of the
>>>> various control points.
>>>>
>>>>
>>>> Note that Bézier functions are not the only mathematical curves. (For
>>>> instance, they cannot exactly match an arc of a circle.) I'm sure there
>>>> are numerous other functions that also produce curves.
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>