
JB
Jordan Brown
Wed, Aug 3, 2022 3:11 AM
Isn't this a general ellipse for axes a and b?
module ellipse(a, b) {
scale([a/b, 1]) circle(b);
}
ellipse(10,20);
Of course, a function that generates the points is useful in other ways.
Isn't this a general ellipse for axes a and b?
module ellipse(a, b) {
scale([a/b, 1]) circle(b);
}
ellipse(10,20);
Of course, a function that generates the points is useful in other ways.

SP
Sanjeev Prabhakar
Wed, Aug 3, 2022 4:01 AM
I am quite occupied these days
Will give it a try this weekend
On Wed, 3 Aug, 2022, 8:21 am Adrian Mariano, avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, openscad@jordan.maileater.net
wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically flow
from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I am quite occupied these days
Will give it a try this weekend
On Wed, 3 Aug, 2022, 8:21 am Adrian Mariano, <avm4@cornell.edu> wrote:
> Here's a challenge for you: draw an "ellipse" polygon with N segments
> that are all the same length that circumscribes a perfect ellipse with
> given semiaxes a and b. I tried to solve this problem and could not find a
> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
> segments the same length---though it's not easy---but the circumscribed
> case eludes me. I think of the inscribed case as, every vertex is located
> on the ellipse and the circumscribed case, every segment is tangent to the
> ellipse
>
> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> In openscad drawing a ellipse is not too difficult
>> Refer following code
>>
>> function to draw an ellipse with semi-major and semi-minor axis "r1" and
>> "r2" respectively and with center "cp" and number of segment "s"
>> /
>> // example:
>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>
>> function ellipse(r1,r2,cp,s=30)=
>> let(
>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>> )sec;
>>
>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net>
>> wrote:
>>
>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>
>>> I created an oval using:
>>> inMm = 25.4;
>>> fullW = 35.5 * inMm;
>>> fullL = 54.5 * inMm;
>>> resize([fullW, fullL, 1])
>>> circle(d=fullW);
>>>
>>>
>>> Tip: use scale() rather than resize(); it previews faster in
>>> complicated cases.
>>>
>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>
>>>
>>> You're taking a circle and stretching it; the result of that stretching
>>> is an ellipse.
>>>
>>> I'm not 100% sure - maybe one of the real math wizards can chime in -
>>> but I think the shape you are asking for would not be an ellipse.
>>>
>>> I believe that an ellipse is fully defined by its major (long) and minor
>>> (short) axis dimensions; the other parts of the curve mathematically flow
>>> from those two measurements.
>>>
>>> You can make something else, but you can't make it using this technique.
>>>
>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>
>>>
>>> You can use a Bézier function.
>>>
>>> Using BOSL2:
>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>
>>> DIY, here's a function that I cobbled together some years ago:
>>>
>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>> // but that yielded either single points or a raft of triangles;
>>> // this yields a vector of points that you can then concatenate
>>> // with other pieces to form a single polygon.
>>> // If we were really clever, I think it would be possible to
>>> // automatically space the output points based on how linear
>>> // the curve is at that point. But right now I'm not that clever.
>>> function BEZ03(u) = pow((1-u), 3);
>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>> function BEZ33(u) = pow(u,3);
>>>
>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>
>>> // p0 - start point
>>> // p1 - control point 1, line departs p0 headed this way
>>> // p2 - control point 2, line arrives at p3 from this way
>>> // p3 - end point
>>> // segs - number of segments
>>> function bez(p0, p1, p2, p3, segs) = [
>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>> ];
>>>
>>> It is that final function bez() that I actually call, e.g.
>>>
>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>
>>> often concatenating the results of several bez() calls together.
>>>
>>> Note that the four coordinates correspond to the coordinates of the
>>> control points in a GUI drawing program: the start point, control point
>>> associated with the start, the control point associated with the end, and
>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>> object in a drawing program and then reading off the coordinates of the
>>> various control points.
>>>
>>>
>>> Note that Bézier functions are not the only mathematical curves. (For
>>> instance, they cannot exactly match an arc of a circle.) I'm sure there
>>> are numerous other functions that also produce curves.
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

RW
Raymond West
Wed, Aug 3, 2022 11:47 AM
sort of interesting. I think whatever you do to a circular object using
scad basic operations, you end up with the same shape curve. For an
oval, you only need to match a quarter of the outline. (I had thought
that a slice through a tilted cone would give something different)
$fn=80;
projection()
translate([0,0,-20])
rotate([0,25,0])
cylinder(h=50,d1=50,d2=20);
scale([.905,1])
#circle(25);
for a one off, as others said, draw a polygon/whatever. I guess a more
interesting result could be by creating slices of a circle( as Jordan
mentioned) but also vary the length of each slice by some other
function. Make it smaller and offset can iron out the bumps if necessary.
Best wishes,
Ray
On 03/08/2022 00:46, Brian Allen wrote:
Hi,
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
Any ideas?
Thanks,
Brian
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
sort of interesting. I think whatever you do to a circular object using
scad basic operations, you end up with the same shape curve. For an
oval, you only need to match a quarter of the outline. (I had thought
that a slice through a tilted cone would give something different)
$fn=80;
projection()
translate([0,0,-20])
rotate([0,25,0])
cylinder(h=50,d1=50,d2=20);
scale([.905,1])
#circle(25);
for a one off, as others said, draw a polygon/whatever. I guess a more
interesting result could be by creating slices of a circle( as Jordan
mentioned) but also vary the length of each slice by some other
function. Make it smaller and offset can iron out the bumps if necessary.
Best wishes,
Ray
On 03/08/2022 00:46, Brian Allen wrote:
> Hi,
>
> I created an oval using:
> inMm = 25.4;
> fullW = 35.5 * inMm;
> fullL = 54.5 * inMm;
> resize([fullW, fullL, 1])
> circle(d=fullW);
>
> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>
> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>
> Any ideas?
>
> Thanks,
> Brian
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

BC
Bob Carlson
Wed, Aug 3, 2022 8:07 PM
Wouldn’t it come pretty close to use you inscribed points as the tangent points, the find the intersections of the tangents?
-Bob
Tucson AZ
On Aug 2, 2022, at 19:50, Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments that are all the same length that circumscribes a perfect ellipse with given semiaxes a and b. I tried to solve this problem and could not find a solution. I can draw an inscribed N segment "ellipse" polygon with all segments the same length---though it's not easy---but the circumscribed case eludes me. I think of the inscribed case as, every vertex is located on the ellipse and the circumscribed case, every segment is tangent to the ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com mailto:sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net mailto:openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in - but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor (short) axis dimensions; the other parts of the curve mathematically flow from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443 https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the control points in a GUI drawing program: the start point, control point associated with the start, the control point associated with the end, and the end point. I have sometimes created OpenSCAD objects by tracing an object in a drawing program and then reading off the coordinates of the various control points.
Note that Bézier functions are not the only mathematical curves. (For instance, they cannot exactly match an arc of a circle.) I'm sure there are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org mailto:discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org mailto:discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Wouldn’t it come pretty close to use you inscribed points as the tangent points, the find the intersections of the tangents?
-Bob
Tucson AZ
On Aug 2, 2022, at 19:50, Adrian Mariano <avm4@cornell.edu> wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments that are all the same length that circumscribes a perfect ellipse with given semiaxes a and b. I tried to solve this problem and could not find a solution. I can draw an *inscribed* N segment "ellipse" polygon with all segments the same length---though it's not easy---but the circumscribed case eludes me. I think of the inscribed case as, every vertex is located on the ellipse and the circumscribed case, every segment is tangent to the ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com <mailto:sprabhakar2006@gmail.com>> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net <mailto:openscad@jordan.maileater.net>> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
> I created an oval using:
> inMm = 25.4;
> fullW = 35.5 * inMm;
> fullL = 54.5 * inMm;
> resize([fullW, fullL, 1])
> circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in complicated cases.
> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in - but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor (short) axis dimensions; the other parts of the curve mathematically flow from those two measurements.
You can make something else, but you can't make it using this technique.
> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2: https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves <https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves>
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443 <https://www.thingiverse.com/thing:8443>
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3*u*(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the control points in a GUI drawing program: the start point, control point associated with the start, the control point associated with the end, and the end point. I have sometimes created OpenSCAD objects by tracing an object in a drawing program and then reading off the coordinates of the various control points.
Note that Bézier functions are not the only mathematical curves. (For instance, they cannot exactly match an arc of a circle.) I'm sure there are numerous other functions that also produce curves.
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org <mailto:discuss-leave@lists.openscad.org>
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org <mailto:discuss-leave@lists.openscad.org>
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org

AM
Adrian Mariano
Wed, Aug 3, 2022 10:26 PM
No, using inscribed equal segment points as tangent points is a terrible
approximation of the equal segment circumscribed polygon. Here's an
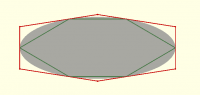
example for N=6 where green is inscribed with equal lengths and red is the
derived circumscribed polygon and some edges are almost double the length
of others. And if the ellipse gets skinnier it gets even worse. Note
also that there are presumably two (symmetric) solutions to the problem,
one tangent at the right point of the ellipse and one with a vertex at the
right tip of the ellipse.
If I recall correctly, I tried to start with this and refine it to get a
good solution, but my approach doesn't converge.
On Wed, Aug 3, 2022 at 4:08 PM Bob Carlson bob@rjcarlson.com wrote:
Wouldn’t it come pretty close to use you inscribed points as the tangent
points, the find the intersections of the tangents?
-Bob
Tucson AZ
On Aug 2, 2022, at 19:50, Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1" and
"r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, openscad@jordan.maileater.net
wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that stretching
is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and minor
(short) axis dimensions; the other parts of the curve mathematically flow
from those two measurements.
You can make something else, but you can't make it using this technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
No, using inscribed equal segment points as tangent points is a terrible
approximation of the equal segment circumscribed polygon. Here's an
example for N=6 where green is inscribed with equal lengths and red is the
derived circumscribed polygon and some edges are almost double the length
of others. And if the ellipse gets skinnier it gets even worse. Note
also that there are presumably two (symmetric) solutions to the problem,
one tangent at the right point of the ellipse and one with a vertex at the
right tip of the ellipse.
If I recall correctly, I tried to start with this and refine it to get a
good solution, but my approach doesn't converge.
On Wed, Aug 3, 2022 at 4:08 PM Bob Carlson <bob@rjcarlson.com> wrote:
> Wouldn’t it come pretty close to use you inscribed points as the tangent
> points, the find the intersections of the tangents?
>
> -Bob
> Tucson AZ
>
>
>
> On Aug 2, 2022, at 19:50, Adrian Mariano <avm4@cornell.edu> wrote:
>
> Here's a challenge for you: draw an "ellipse" polygon with N segments
> that are all the same length that circumscribes a perfect ellipse with
> given semiaxes a and b. I tried to solve this problem and could not find a
> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
> segments the same length---though it's not easy---but the circumscribed
> case eludes me. I think of the inscribed case as, every vertex is located
> on the ellipse and the circumscribed case, every segment is tangent to the
> ellipse
>
> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> In openscad drawing a ellipse is not too difficult
>> Refer following code
>>
>> function to draw an ellipse with semi-major and semi-minor axis "r1" and
>> "r2" respectively and with center "cp" and number of segment "s"
>> /
>> // example:
>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>
>> function ellipse(r1,r2,cp,s=30)=
>> let(
>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>> )sec;
>>
>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <openscad@jordan.maileater.net>
>> wrote:
>>
>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>
>>> I created an oval using:
>>> inMm = 25.4;
>>> fullW = 35.5 * inMm;
>>> fullL = 54.5 * inMm;
>>> resize([fullW, fullL, 1])
>>> circle(d=fullW);
>>>
>>>
>>> Tip: use scale() rather than resize(); it previews faster in
>>> complicated cases.
>>>
>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>
>>>
>>> You're taking a circle and stretching it; the result of that stretching
>>> is an ellipse.
>>>
>>> I'm not 100% sure - maybe one of the real math wizards can chime in -
>>> but I think the shape you are asking for would not be an ellipse.
>>>
>>> I believe that an ellipse is fully defined by its major (long) and minor
>>> (short) axis dimensions; the other parts of the curve mathematically flow
>>> from those two measurements.
>>>
>>> You can make something else, but you can't make it using this technique.
>>>
>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>
>>>
>>> You can use a Bézier function.
>>>
>>> Using BOSL2:
>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>
>>> DIY, here's a function that I cobbled together some years ago:
>>>
>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>> // but that yielded either single points or a raft of triangles;
>>> // this yields a vector of points that you can then concatenate
>>> // with other pieces to form a single polygon.
>>> // If we were really clever, I think it would be possible to
>>> // automatically space the output points based on how linear
>>> // the curve is at that point. But right now I'm not that clever.
>>> function BEZ03(u) = pow((1-u), 3);
>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>> function BEZ33(u) = pow(u,3);
>>>
>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>
>>> // p0 - start point
>>> // p1 - control point 1, line departs p0 headed this way
>>> // p2 - control point 2, line arrives at p3 from this way
>>> // p3 - end point
>>> // segs - number of segments
>>> function bez(p0, p1, p2, p3, segs) = [
>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>> ];
>>>
>>> It is that final function bez() that I actually call, e.g.
>>>
>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>
>>> often concatenating the results of several bez() calls together.
>>>
>>> Note that the four coordinates correspond to the coordinates of the
>>> control points in a GUI drawing program: the start point, control point
>>> associated with the start, the control point associated with the end, and
>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>> object in a drawing program and then reading off the coordinates of the
>>> various control points.
>>>
>>>
>>> Note that Bézier functions are not the only mathematical curves. (For
>>> instance, they cannot exactly match an arc of a circle.) I'm sure there
>>> are numerous other functions that also produce curves.
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

FH
Father Horton
Wed, Aug 3, 2022 11:40 PM
I think our emails crossed. I was addressing how to approximate an ellipse
with constant-length segments in general, not how to solve your problem.
When I had to do something similar, I used polar coordinates and stepped up
the value of theta until the distance from the previous point was correct.
(In the constant-length version, I'd keep a running total of the maximum
desired length so that round-off errors don't accumulate.)
Figuring out the circumscribed polygon is, as you note, a greater
challenge. I can visualize how to do it for n = 4, but it doesn't
extrapolate at all.
On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano avm4@cornell.edu wrote:
Eh, there's no such thing as "brute force" in this situation. Step
through what with sufficiently small steps? Of course an iterative
algorithm is necessary. This is true for most interesting problems. No
big deal. Show me an iterative algorithm that converges to the
circumscribing polygon. When I tried to devise such an algorithm I
couldn't find one that would converge. Writing an algorithm that would
converge to the inscribed polygon seemed to be straight forward. Note
also that computing arc length of the ellipse doesn't really help here.
You can do that by solving an elliptical integral, or summing up small
segments. But what's the connection between arc length of the ellipse and
a circumscribing polygon with equal segment lengths? If there's a
connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton fatherhorton@gmail.com
wrote:
Except by brute force (step through it with sufficiently small steps),
it’s not possible because there’s no closed form expression for the
distance between two points on a general ellipse (as opposed to special
cases like a circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1"
and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that
stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and
minor (short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this
technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves. (For
instance, they cannot exactly match an arc of a circle.) I'm sure there
are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I think our emails crossed. I was addressing how to approximate an ellipse
with constant-length segments in general, not how to solve your problem.
When I had to do something similar, I used polar coordinates and stepped up
the value of theta until the distance from the previous point was correct.
(In the constant-length version, I'd keep a running total of the maximum
desired length so that round-off errors don't accumulate.)
Figuring out the circumscribed polygon is, as you note, a greater
challenge. I can visualize how to do it for n = 4, but it doesn't
extrapolate at all.
On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano <avm4@cornell.edu> wrote:
> Eh, there's no such thing as "brute force" in this situation. Step
> through *what* with sufficiently small steps? Of course an iterative
> algorithm is necessary. This is true for most interesting problems. No
> big deal. Show me an iterative algorithm that converges to the
> circumscribing polygon. When I tried to devise such an algorithm I
> couldn't find one that would converge. Writing an algorithm that would
> converge to the *inscribed* polygon seemed to be straight forward. Note
> also that computing arc length of the ellipse doesn't really help here.
> You can do that by solving an elliptical integral, or summing up small
> segments. But what's the connection between arc length of the ellipse and
> a circumscribing polygon with equal segment lengths? If there's a
> connection, I don't see it.
>
> On Tue, Aug 2, 2022 at 10:56 PM Father Horton <fatherhorton@gmail.com>
> wrote:
>
>> Except by brute force (step through it with sufficiently small steps),
>> it’s not possible because there’s no closed form expression for the
>> distance between two points on a general ellipse (as opposed to special
>> cases like a circle).
>>
>> On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Here's a challenge for you: draw an "ellipse" polygon with N segments
>>> that are all the same length that circumscribes a perfect ellipse with
>>> given semiaxes a and b. I tried to solve this problem and could not find a
>>> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
>>> segments the same length---though it's not easy---but the circumscribed
>>> case eludes me. I think of the inscribed case as, every vertex is located
>>> on the ellipse and the circumscribed case, every segment is tangent to the
>>> ellipse
>>>
>>> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> In openscad drawing a ellipse is not too difficult
>>>> Refer following code
>>>>
>>>> function to draw an ellipse with semi-major and semi-minor axis "r1"
>>>> and "r2" respectively and with center "cp" and number of segment "s"
>>>> /
>>>> // example:
>>>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>>>
>>>> function ellipse(r1,r2,cp,s=30)=
>>>> let(
>>>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>>>> )sec;
>>>>
>>>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
>>>> openscad@jordan.maileater.net> wrote:
>>>>
>>>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>>>
>>>>> I created an oval using:
>>>>> inMm = 25.4;
>>>>> fullW = 35.5 * inMm;
>>>>> fullL = 54.5 * inMm;
>>>>> resize([fullW, fullL, 1])
>>>>> circle(d=fullW);
>>>>>
>>>>>
>>>>> Tip: use scale() rather than resize(); it previews faster in
>>>>> complicated cases.
>>>>>
>>>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>>>
>>>>>
>>>>> You're taking a circle and stretching it; the result of that
>>>>> stretching is an ellipse.
>>>>>
>>>>> I'm not 100% sure - maybe one of the real math wizards can chime in -
>>>>> but I think the shape you are asking for would not be an ellipse.
>>>>>
>>>>> I believe that an ellipse is fully defined by its major (long) and
>>>>> minor (short) axis dimensions; the other parts of the curve mathematically
>>>>> flow from those two measurements.
>>>>>
>>>>> You can make something else, but you can't make it using this
>>>>> technique.
>>>>>
>>>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>>>
>>>>>
>>>>> You can use a Bézier function.
>>>>>
>>>>> Using BOSL2:
>>>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>>>
>>>>> DIY, here's a function that I cobbled together some years ago:
>>>>>
>>>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>>>> // but that yielded either single points or a raft of triangles;
>>>>> // this yields a vector of points that you can then concatenate
>>>>> // with other pieces to form a single polygon.
>>>>> // If we were really clever, I think it would be possible to
>>>>> // automatically space the output points based on how linear
>>>>> // the curve is at that point. But right now I'm not that clever.
>>>>> function BEZ03(u) = pow((1-u), 3);
>>>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>>>> function BEZ33(u) = pow(u,3);
>>>>>
>>>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>>>
>>>>> // p0 - start point
>>>>> // p1 - control point 1, line departs p0 headed this way
>>>>> // p2 - control point 2, line arrives at p3 from this way
>>>>> // p3 - end point
>>>>> // segs - number of segments
>>>>> function bez(p0, p1, p2, p3, segs) = [
>>>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>>>> ];
>>>>>
>>>>> It is that final function bez() that I actually call, e.g.
>>>>>
>>>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>>>
>>>>> often concatenating the results of several bez() calls together.
>>>>>
>>>>> Note that the four coordinates correspond to the coordinates of the
>>>>> control points in a GUI drawing program: the start point, control point
>>>>> associated with the start, the control point associated with the end, and
>>>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>>>> object in a drawing program and then reading off the coordinates of the
>>>>> various control points.
>>>>>
>>>>>
>>>>> Note that Bézier functions are not the only mathematical curves. (For
>>>>> instance, they cannot exactly match an arc of a circle.) I'm sure there
>>>>> are numerous other functions that also produce curves.
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Thu, Aug 4, 2022 12:13 AM
I think you need to be a little careful about defining what you want to
do. If you want to approximate an ellipse with points that are distributed
uniformly over the ellipse, that could be done by approximating the arc
length of the ellipse to find the necessary points---e.g. advance distance
d along the ellipse at each step. But if you want to approximate an
ellipse with a polygon with equal length sides, that approach does not do
it, because the length of the segments will not be constant as the span
sections of the ellipse with differing curvature. And since the perimeter
of the desired polygon is unknown, you can't just step it out analogously.
The circle doesn't present this challenge due to having constant
curvature.
On Wed, Aug 3, 2022 at 7:41 PM Father Horton fatherhorton@gmail.com wrote:
I think our emails crossed. I was addressing how to approximate an ellipse
with constant-length segments in general, not how to solve your problem.
When I had to do something similar, I used polar coordinates and stepped up
the value of theta until the distance from the previous point was correct.
(In the constant-length version, I'd keep a running total of the maximum
desired length so that round-off errors don't accumulate.)
Figuring out the circumscribed polygon is, as you note, a greater
challenge. I can visualize how to do it for n = 4, but it doesn't
extrapolate at all.
On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano avm4@cornell.edu wrote:
Eh, there's no such thing as "brute force" in this situation. Step
through what with sufficiently small steps? Of course an iterative
algorithm is necessary. This is true for most interesting problems. No
big deal. Show me an iterative algorithm that converges to the
circumscribing polygon. When I tried to devise such an algorithm I
couldn't find one that would converge. Writing an algorithm that would
converge to the inscribed polygon seemed to be straight forward. Note
also that computing arc length of the ellipse doesn't really help here.
You can do that by solving an elliptical integral, or summing up small
segments. But what's the connection between arc length of the ellipse and
a circumscribing polygon with equal segment lengths? If there's a
connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton fatherhorton@gmail.com
wrote:
Except by brute force (step through it with sufficiently small steps),
it’s not possible because there’s no closed form expression for the
distance between two points on a general ellipse (as opposed to special
cases like a circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1"
and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that
stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in -
but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and
minor (short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this
technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves.
(For instance, they cannot exactly match an arc of a circle.) I'm sure
there are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I think you need to be a little careful about defining what you want to
do. If you want to approximate an ellipse with points that are distributed
uniformly over the ellipse, that could be done by approximating the arc
length of the ellipse to find the necessary points---e.g. advance distance
d along the ellipse at each step. But if you want to approximate an
ellipse with a polygon with equal length sides, that approach does not do
it, because the length of the segments will not be constant as the span
sections of the ellipse with differing curvature. And since the perimeter
of the desired polygon is unknown, you can't just step it out analogously.
The circle doesn't present this challenge due to having constant
curvature.
On Wed, Aug 3, 2022 at 7:41 PM Father Horton <fatherhorton@gmail.com> wrote:
> I think our emails crossed. I was addressing how to approximate an ellipse
> with constant-length segments in general, not how to solve your problem.
> When I had to do something similar, I used polar coordinates and stepped up
> the value of theta until the distance from the previous point was correct.
> (In the constant-length version, I'd keep a running total of the maximum
> desired length so that round-off errors don't accumulate.)
>
> Figuring out the circumscribed polygon is, as you note, a greater
> challenge. I can visualize how to do it for n = 4, but it doesn't
> extrapolate at all.
>
> On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Eh, there's no such thing as "brute force" in this situation. Step
>> through *what* with sufficiently small steps? Of course an iterative
>> algorithm is necessary. This is true for most interesting problems. No
>> big deal. Show me an iterative algorithm that converges to the
>> circumscribing polygon. When I tried to devise such an algorithm I
>> couldn't find one that would converge. Writing an algorithm that would
>> converge to the *inscribed* polygon seemed to be straight forward. Note
>> also that computing arc length of the ellipse doesn't really help here.
>> You can do that by solving an elliptical integral, or summing up small
>> segments. But what's the connection between arc length of the ellipse and
>> a circumscribing polygon with equal segment lengths? If there's a
>> connection, I don't see it.
>>
>> On Tue, Aug 2, 2022 at 10:56 PM Father Horton <fatherhorton@gmail.com>
>> wrote:
>>
>>> Except by brute force (step through it with sufficiently small steps),
>>> it’s not possible because there’s no closed form expression for the
>>> distance between two points on a general ellipse (as opposed to special
>>> cases like a circle).
>>>
>>> On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> Here's a challenge for you: draw an "ellipse" polygon with N segments
>>>> that are all the same length that circumscribes a perfect ellipse with
>>>> given semiaxes a and b. I tried to solve this problem and could not find a
>>>> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
>>>> segments the same length---though it's not easy---but the circumscribed
>>>> case eludes me. I think of the inscribed case as, every vertex is located
>>>> on the ellipse and the circumscribed case, every segment is tangent to the
>>>> ellipse
>>>>
>>>> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
>>>> sprabhakar2006@gmail.com> wrote:
>>>>
>>>>> In openscad drawing a ellipse is not too difficult
>>>>> Refer following code
>>>>>
>>>>> function to draw an ellipse with semi-major and semi-minor axis "r1"
>>>>> and "r2" respectively and with center "cp" and number of segment "s"
>>>>> /
>>>>> // example:
>>>>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>>>>
>>>>> function ellipse(r1,r2,cp,s=30)=
>>>>> let(
>>>>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>>>>> )sec;
>>>>>
>>>>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
>>>>> openscad@jordan.maileater.net> wrote:
>>>>>
>>>>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>>>>
>>>>>> I created an oval using:
>>>>>> inMm = 25.4;
>>>>>> fullW = 35.5 * inMm;
>>>>>> fullL = 54.5 * inMm;
>>>>>> resize([fullW, fullL, 1])
>>>>>> circle(d=fullW);
>>>>>>
>>>>>>
>>>>>> Tip: use scale() rather than resize(); it previews faster in
>>>>>> complicated cases.
>>>>>>
>>>>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>>>>
>>>>>>
>>>>>> You're taking a circle and stretching it; the result of that
>>>>>> stretching is an ellipse.
>>>>>>
>>>>>> I'm not 100% sure - maybe one of the real math wizards can chime in -
>>>>>> but I think the shape you are asking for would not be an ellipse.
>>>>>>
>>>>>> I believe that an ellipse is fully defined by its major (long) and
>>>>>> minor (short) axis dimensions; the other parts of the curve mathematically
>>>>>> flow from those two measurements.
>>>>>>
>>>>>> You can make something else, but you can't make it using this
>>>>>> technique.
>>>>>>
>>>>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>>>>
>>>>>>
>>>>>> You can use a Bézier function.
>>>>>>
>>>>>> Using BOSL2:
>>>>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>>>>
>>>>>> DIY, here's a function that I cobbled together some years ago:
>>>>>>
>>>>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>>>>> // but that yielded either single points or a raft of triangles;
>>>>>> // this yields a vector of points that you can then concatenate
>>>>>> // with other pieces to form a single polygon.
>>>>>> // If we were really clever, I think it would be possible to
>>>>>> // automatically space the output points based on how linear
>>>>>> // the curve is at that point. But right now I'm not that clever.
>>>>>> function BEZ03(u) = pow((1-u), 3);
>>>>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>>>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>>>>> function BEZ33(u) = pow(u,3);
>>>>>>
>>>>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>>>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>>>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>>>>
>>>>>> // p0 - start point
>>>>>> // p1 - control point 1, line departs p0 headed this way
>>>>>> // p2 - control point 2, line arrives at p3 from this way
>>>>>> // p3 - end point
>>>>>> // segs - number of segments
>>>>>> function bez(p0, p1, p2, p3, segs) = [
>>>>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>>>>> ];
>>>>>>
>>>>>> It is that final function bez() that I actually call, e.g.
>>>>>>
>>>>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>>>>
>>>>>> often concatenating the results of several bez() calls together.
>>>>>>
>>>>>> Note that the four coordinates correspond to the coordinates of the
>>>>>> control points in a GUI drawing program: the start point, control point
>>>>>> associated with the start, the control point associated with the end, and
>>>>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>>>>> object in a drawing program and then reading off the coordinates of the
>>>>>> various control points.
>>>>>>
>>>>>>
>>>>>> Note that Bézier functions are not the only mathematical curves.
>>>>>> (For instance, they cannot exactly match an arc of a circle.) I'm sure
>>>>>> there are numerous other functions that also produce curves.
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Fri, Aug 5, 2022 4:43 PM
I think circumscribed polygon segments cannot be equal lengths.
inscribed ones may be approximately equal, but would be a very tough
problem to solve.
I tried something.
On Thu, 4 Aug 2022 at 05:44, Adrian Mariano avm4@cornell.edu wrote:
I think you need to be a little careful about defining what you want to
do. If you want to approximate an ellipse with points that are distributed
uniformly over the ellipse, that could be done by approximating the arc
length of the ellipse to find the necessary points---e.g. advance distance
d along the ellipse at each step. But if you want to approximate an
ellipse with a polygon with equal length sides, that approach does not do
it, because the length of the segments will not be constant as the span
sections of the ellipse with differing curvature. And since the perimeter
of the desired polygon is unknown, you can't just step it out analogously.
The circle doesn't present this challenge due to having constant
curvature.
On Wed, Aug 3, 2022 at 7:41 PM Father Horton fatherhorton@gmail.com
wrote:
I think our emails crossed. I was addressing how to approximate an
ellipse with constant-length segments in general, not how to solve your
problem. When I had to do something similar, I used polar coordinates and
stepped up the value of theta until the distance from the previous point
was correct. (In the constant-length version, I'd keep a running total of
the maximum desired length so that round-off errors don't accumulate.)
Figuring out the circumscribed polygon is, as you note, a greater
challenge. I can visualize how to do it for n = 4, but it doesn't
extrapolate at all.
On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano avm4@cornell.edu wrote:
Eh, there's no such thing as "brute force" in this situation. Step
through what with sufficiently small steps? Of course an iterative
algorithm is necessary. This is true for most interesting problems. No
big deal. Show me an iterative algorithm that converges to the
circumscribing polygon. When I tried to devise such an algorithm I
couldn't find one that would converge. Writing an algorithm that would
converge to the inscribed polygon seemed to be straight forward. Note
also that computing arc length of the ellipse doesn't really help here.
You can do that by solving an elliptical integral, or summing up small
segments. But what's the connection between arc length of the ellipse and
a circumscribing polygon with equal segment lengths? If there's a
connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton fatherhorton@gmail.com
wrote:
Except by brute force (step through it with sufficiently small steps),
it’s not possible because there’s no closed form expression for the
distance between two points on a general ellipse (as opposed to special
cases like a circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu wrote:
Here's a challenge for you: draw an "ellipse" polygon with N segments
that are all the same length that circumscribes a perfect ellipse with
given semiaxes a and b. I tried to solve this problem and could not find a
solution. I can draw an inscribed N segment "ellipse" polygon with all
segments the same length---though it's not easy---but the circumscribed
case eludes me. I think of the inscribed case as, every vertex is located
on the ellipse and the circumscribed case, every segment is tangent to the
ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1"
and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that
stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in
- but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and
minor (short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this
technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves.
(For instance, they cannot exactly match an arc of a circle.) I'm sure
there are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I think circumscribed polygon segments cannot be equal lengths.
inscribed ones may be approximately equal, but would be a very tough
problem to solve.
I tried something.
On Thu, 4 Aug 2022 at 05:44, Adrian Mariano <avm4@cornell.edu> wrote:
> I think you need to be a little careful about defining what you want to
> do. If you want to approximate an ellipse with points that are distributed
> uniformly over the ellipse, that could be done by approximating the arc
> length of the ellipse to find the necessary points---e.g. advance distance
> d along the ellipse at each step. But if you want to approximate an
> ellipse with a polygon with equal length sides, that approach does not do
> it, because the length of the segments will not be constant as the span
> sections of the ellipse with differing curvature. And since the perimeter
> of the desired polygon is unknown, you can't just step it out analogously.
> The circle doesn't present this challenge due to having constant
> curvature.
>
> On Wed, Aug 3, 2022 at 7:41 PM Father Horton <fatherhorton@gmail.com>
> wrote:
>
>> I think our emails crossed. I was addressing how to approximate an
>> ellipse with constant-length segments in general, not how to solve your
>> problem. When I had to do something similar, I used polar coordinates and
>> stepped up the value of theta until the distance from the previous point
>> was correct. (In the constant-length version, I'd keep a running total of
>> the maximum desired length so that round-off errors don't accumulate.)
>>
>> Figuring out the circumscribed polygon is, as you note, a greater
>> challenge. I can visualize how to do it for n = 4, but it doesn't
>> extrapolate at all.
>>
>> On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Eh, there's no such thing as "brute force" in this situation. Step
>>> through *what* with sufficiently small steps? Of course an iterative
>>> algorithm is necessary. This is true for most interesting problems. No
>>> big deal. Show me an iterative algorithm that converges to the
>>> circumscribing polygon. When I tried to devise such an algorithm I
>>> couldn't find one that would converge. Writing an algorithm that would
>>> converge to the *inscribed* polygon seemed to be straight forward. Note
>>> also that computing arc length of the ellipse doesn't really help here.
>>> You can do that by solving an elliptical integral, or summing up small
>>> segments. But what's the connection between arc length of the ellipse and
>>> a circumscribing polygon with equal segment lengths? If there's a
>>> connection, I don't see it.
>>>
>>> On Tue, Aug 2, 2022 at 10:56 PM Father Horton <fatherhorton@gmail.com>
>>> wrote:
>>>
>>>> Except by brute force (step through it with sufficiently small steps),
>>>> it’s not possible because there’s no closed form expression for the
>>>> distance between two points on a general ellipse (as opposed to special
>>>> cases like a circle).
>>>>
>>>> On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>>>
>>>>> Here's a challenge for you: draw an "ellipse" polygon with N segments
>>>>> that are all the same length that circumscribes a perfect ellipse with
>>>>> given semiaxes a and b. I tried to solve this problem and could not find a
>>>>> solution. I can draw an *inscribed* N segment "ellipse" polygon with all
>>>>> segments the same length---though it's not easy---but the circumscribed
>>>>> case eludes me. I think of the inscribed case as, every vertex is located
>>>>> on the ellipse and the circumscribed case, every segment is tangent to the
>>>>> ellipse
>>>>>
>>>>> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>
>>>>>> In openscad drawing a ellipse is not too difficult
>>>>>> Refer following code
>>>>>>
>>>>>> function to draw an ellipse with semi-major and semi-minor axis "r1"
>>>>>> and "r2" respectively and with center "cp" and number of segment "s"
>>>>>> /
>>>>>> // example:
>>>>>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>>>>>
>>>>>> function ellipse(r1,r2,cp,s=30)=
>>>>>> let(
>>>>>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>>>>>> )sec;
>>>>>>
>>>>>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
>>>>>> openscad@jordan.maileater.net> wrote:
>>>>>>
>>>>>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>>>>>
>>>>>>> I created an oval using:
>>>>>>> inMm = 25.4;
>>>>>>> fullW = 35.5 * inMm;
>>>>>>> fullL = 54.5 * inMm;
>>>>>>> resize([fullW, fullL, 1])
>>>>>>> circle(d=fullW);
>>>>>>>
>>>>>>>
>>>>>>> Tip: use scale() rather than resize(); it previews faster in
>>>>>>> complicated cases.
>>>>>>>
>>>>>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>>>>>
>>>>>>>
>>>>>>> You're taking a circle and stretching it; the result of that
>>>>>>> stretching is an ellipse.
>>>>>>>
>>>>>>> I'm not 100% sure - maybe one of the real math wizards can chime in
>>>>>>> - but I think the shape you are asking for would not be an ellipse.
>>>>>>>
>>>>>>> I believe that an ellipse is fully defined by its major (long) and
>>>>>>> minor (short) axis dimensions; the other parts of the curve mathematically
>>>>>>> flow from those two measurements.
>>>>>>>
>>>>>>> You can make something else, but you can't make it using this
>>>>>>> technique.
>>>>>>>
>>>>>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>>>>>
>>>>>>>
>>>>>>> You can use a Bézier function.
>>>>>>>
>>>>>>> Using BOSL2:
>>>>>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>>>>>
>>>>>>> DIY, here's a function that I cobbled together some years ago:
>>>>>>>
>>>>>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>>>>>> // but that yielded either single points or a raft of triangles;
>>>>>>> // this yields a vector of points that you can then concatenate
>>>>>>> // with other pieces to form a single polygon.
>>>>>>> // If we were really clever, I think it would be possible to
>>>>>>> // automatically space the output points based on how linear
>>>>>>> // the curve is at that point. But right now I'm not that clever.
>>>>>>> function BEZ03(u) = pow((1-u), 3);
>>>>>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>>>>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>>>>>> function BEZ33(u) = pow(u,3);
>>>>>>>
>>>>>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>>>>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>>>>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>>>>>
>>>>>>> // p0 - start point
>>>>>>> // p1 - control point 1, line departs p0 headed this way
>>>>>>> // p2 - control point 2, line arrives at p3 from this way
>>>>>>> // p3 - end point
>>>>>>> // segs - number of segments
>>>>>>> function bez(p0, p1, p2, p3, segs) = [
>>>>>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>>>>>> ];
>>>>>>>
>>>>>>> It is that final function bez() that I actually call, e.g.
>>>>>>>
>>>>>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>>>>>
>>>>>>> often concatenating the results of several bez() calls together.
>>>>>>>
>>>>>>> Note that the four coordinates correspond to the coordinates of the
>>>>>>> control points in a GUI drawing program: the start point, control point
>>>>>>> associated with the start, the control point associated with the end, and
>>>>>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>>>>>> object in a drawing program and then reading off the coordinates of the
>>>>>>> various control points.
>>>>>>>
>>>>>>>
>>>>>>> Note that Bézier functions are not the only mathematical curves.
>>>>>>> (For instance, they cannot exactly match an arc of a circle.) I'm sure
>>>>>>> there are numerous other functions that also produce curves.
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Fri, Aug 5, 2022 8:57 PM
You think that a circumscribing polygon with equal length segments does not
exist?? I'm skeptical of this claim.
For circumscribed, it's not so hard. You start with a uniform-in-angle
point distribution, compute the segment lengths, compare to the mean
segment length to get an error, and then compute an adjustment based on the
error. It converges quickly.
So for example, I have segments lengths of:
ECHO: [5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297,
5.57297]
Maybe not exactly equal, since tolerance is 1e-9, but surely good enough.
[image: image.png]
The code for this is in BOSL2 in shapes2d.scad. A similar algorithm should
exist for the circumscribed case, but as I said, my efforts to find it have
failed.
On Fri, Aug 5, 2022 at 12:44 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I think circumscribed polygon segments cannot be equal lengths.
inscribed ones may be approximately equal, but would be a very tough
problem to solve.
I tried something.
On Thu, 4 Aug 2022 at 05:44, Adrian Mariano avm4@cornell.edu wrote:
I think you need to be a little careful about defining what you want to
do. If you want to approximate an ellipse with points that are distributed
uniformly over the ellipse, that could be done by approximating the arc
length of the ellipse to find the necessary points---e.g. advance distance
d along the ellipse at each step. But if you want to approximate an
ellipse with a polygon with equal length sides, that approach does not do
it, because the length of the segments will not be constant as the span
sections of the ellipse with differing curvature. And since the perimeter
of the desired polygon is unknown, you can't just step it out analogously.
The circle doesn't present this challenge due to having constant
curvature.
On Wed, Aug 3, 2022 at 7:41 PM Father Horton fatherhorton@gmail.com
wrote:
I think our emails crossed. I was addressing how to approximate an
ellipse with constant-length segments in general, not how to solve your
problem. When I had to do something similar, I used polar coordinates and
stepped up the value of theta until the distance from the previous point
was correct. (In the constant-length version, I'd keep a running total of
the maximum desired length so that round-off errors don't accumulate.)
Figuring out the circumscribed polygon is, as you note, a greater
challenge. I can visualize how to do it for n = 4, but it doesn't
extrapolate at all.
On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano avm4@cornell.edu wrote:
Eh, there's no such thing as "brute force" in this situation. Step
through what with sufficiently small steps? Of course an iterative
algorithm is necessary. This is true for most interesting problems. No
big deal. Show me an iterative algorithm that converges to the
circumscribing polygon. When I tried to devise such an algorithm I
couldn't find one that would converge. Writing an algorithm that would
converge to the inscribed polygon seemed to be straight forward. Note
also that computing arc length of the ellipse doesn't really help here.
You can do that by solving an elliptical integral, or summing up small
segments. But what's the connection between arc length of the ellipse and
a circumscribing polygon with equal segment lengths? If there's a
connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton fatherhorton@gmail.com
wrote:
Except by brute force (step through it with sufficiently small steps),
it’s not possible because there’s no closed form expression for the
distance between two points on a general ellipse (as opposed to special
cases like a circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu
wrote:
Here's a challenge for you: draw an "ellipse" polygon with N
segments that are all the same length that circumscribes a perfect ellipse
with given semiaxes a and b. I tried to solve this problem and could not
find a solution. I can draw an inscribed N segment "ellipse" polygon
with all segments the same length---though it's not easy---but the
circumscribed case eludes me. I think of the inscribed case as, every
vertex is located on the ellipse and the circumscribed case, every segment
is tangent to the ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis "r1"
and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that
stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime in
- but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and
minor (short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this
technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of the
control points in a GUI drawing program: the start point, control point
associated with the start, the control point associated with the end, and
the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves.
(For instance, they cannot exactly match an arc of a circle.) I'm sure
there are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
You think that a circumscribing polygon with equal length segments does not
exist?? I'm skeptical of this claim.
For circumscribed, it's not so hard. You start with a uniform-in-angle
point distribution, compute the segment lengths, compare to the mean
segment length to get an error, and then compute an adjustment based on the
error. It converges quickly.
So for example, I have segments lengths of:
ECHO: [5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297,
5.57297]
Maybe not exactly equal, since tolerance is 1e-9, but surely good enough.
[image: image.png]
The code for this is in BOSL2 in shapes2d.scad. A similar algorithm should
exist for the circumscribed case, but as I said, my efforts to find it have
failed.
On Fri, Aug 5, 2022 at 12:44 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I think circumscribed polygon segments cannot be equal lengths.
> inscribed ones may be approximately equal, but would be a very tough
> problem to solve.
> I tried something.
>
>
>
> On Thu, 4 Aug 2022 at 05:44, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> I think you need to be a little careful about defining what you want to
>> do. If you want to approximate an ellipse with points that are distributed
>> uniformly over the ellipse, that could be done by approximating the arc
>> length of the ellipse to find the necessary points---e.g. advance distance
>> d along the ellipse at each step. But if you want to approximate an
>> ellipse with a polygon with equal length sides, that approach does not do
>> it, because the length of the segments will not be constant as the span
>> sections of the ellipse with differing curvature. And since the perimeter
>> of the desired polygon is unknown, you can't just step it out analogously.
>> The circle doesn't present this challenge due to having constant
>> curvature.
>>
>> On Wed, Aug 3, 2022 at 7:41 PM Father Horton <fatherhorton@gmail.com>
>> wrote:
>>
>>> I think our emails crossed. I was addressing how to approximate an
>>> ellipse with constant-length segments in general, not how to solve your
>>> problem. When I had to do something similar, I used polar coordinates and
>>> stepped up the value of theta until the distance from the previous point
>>> was correct. (In the constant-length version, I'd keep a running total of
>>> the maximum desired length so that round-off errors don't accumulate.)
>>>
>>> Figuring out the circumscribed polygon is, as you note, a greater
>>> challenge. I can visualize how to do it for n = 4, but it doesn't
>>> extrapolate at all.
>>>
>>> On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> Eh, there's no such thing as "brute force" in this situation. Step
>>>> through *what* with sufficiently small steps? Of course an iterative
>>>> algorithm is necessary. This is true for most interesting problems. No
>>>> big deal. Show me an iterative algorithm that converges to the
>>>> circumscribing polygon. When I tried to devise such an algorithm I
>>>> couldn't find one that would converge. Writing an algorithm that would
>>>> converge to the *inscribed* polygon seemed to be straight forward. Note
>>>> also that computing arc length of the ellipse doesn't really help here.
>>>> You can do that by solving an elliptical integral, or summing up small
>>>> segments. But what's the connection between arc length of the ellipse and
>>>> a circumscribing polygon with equal segment lengths? If there's a
>>>> connection, I don't see it.
>>>>
>>>> On Tue, Aug 2, 2022 at 10:56 PM Father Horton <fatherhorton@gmail.com>
>>>> wrote:
>>>>
>>>>> Except by brute force (step through it with sufficiently small steps),
>>>>> it’s not possible because there’s no closed form expression for the
>>>>> distance between two points on a general ellipse (as opposed to special
>>>>> cases like a circle).
>>>>>
>>>>> On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu>
>>>>> wrote:
>>>>>
>>>>>> Here's a challenge for you: draw an "ellipse" polygon with N
>>>>>> segments that are all the same length that circumscribes a perfect ellipse
>>>>>> with given semiaxes a and b. I tried to solve this problem and could not
>>>>>> find a solution. I can draw an *inscribed* N segment "ellipse" polygon
>>>>>> with all segments the same length---though it's not easy---but the
>>>>>> circumscribed case eludes me. I think of the inscribed case as, every
>>>>>> vertex is located on the ellipse and the circumscribed case, every segment
>>>>>> is tangent to the ellipse
>>>>>>
>>>>>> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>
>>>>>>> In openscad drawing a ellipse is not too difficult
>>>>>>> Refer following code
>>>>>>>
>>>>>>> function to draw an ellipse with semi-major and semi-minor axis "r1"
>>>>>>> and "r2" respectively and with center "cp" and number of segment "s"
>>>>>>> /
>>>>>>> // example:
>>>>>>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>>>>>>
>>>>>>> function ellipse(r1,r2,cp,s=30)=
>>>>>>> let(
>>>>>>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>>>>>>> )sec;
>>>>>>>
>>>>>>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
>>>>>>> openscad@jordan.maileater.net> wrote:
>>>>>>>
>>>>>>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>>>>>>
>>>>>>>> I created an oval using:
>>>>>>>> inMm = 25.4;
>>>>>>>> fullW = 35.5 * inMm;
>>>>>>>> fullL = 54.5 * inMm;
>>>>>>>> resize([fullW, fullL, 1])
>>>>>>>> circle(d=fullW);
>>>>>>>>
>>>>>>>>
>>>>>>>> Tip: use scale() rather than resize(); it previews faster in
>>>>>>>> complicated cases.
>>>>>>>>
>>>>>>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>>>>>>
>>>>>>>>
>>>>>>>> You're taking a circle and stretching it; the result of that
>>>>>>>> stretching is an ellipse.
>>>>>>>>
>>>>>>>> I'm not 100% sure - maybe one of the real math wizards can chime in
>>>>>>>> - but I think the shape you are asking for would not be an ellipse.
>>>>>>>>
>>>>>>>> I believe that an ellipse is fully defined by its major (long) and
>>>>>>>> minor (short) axis dimensions; the other parts of the curve mathematically
>>>>>>>> flow from those two measurements.
>>>>>>>>
>>>>>>>> You can make something else, but you can't make it using this
>>>>>>>> technique.
>>>>>>>>
>>>>>>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>>>>>>
>>>>>>>>
>>>>>>>> You can use a Bézier function.
>>>>>>>>
>>>>>>>> Using BOSL2:
>>>>>>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>>>>>>
>>>>>>>> DIY, here's a function that I cobbled together some years ago:
>>>>>>>>
>>>>>>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>>>>>>> // but that yielded either single points or a raft of triangles;
>>>>>>>> // this yields a vector of points that you can then concatenate
>>>>>>>> // with other pieces to form a single polygon.
>>>>>>>> // If we were really clever, I think it would be possible to
>>>>>>>> // automatically space the output points based on how linear
>>>>>>>> // the curve is at that point. But right now I'm not that clever.
>>>>>>>> function BEZ03(u) = pow((1-u), 3);
>>>>>>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>>>>>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>>>>>>> function BEZ33(u) = pow(u,3);
>>>>>>>>
>>>>>>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>>>>>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>>>>>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>>>>>>
>>>>>>>> // p0 - start point
>>>>>>>> // p1 - control point 1, line departs p0 headed this way
>>>>>>>> // p2 - control point 2, line arrives at p3 from this way
>>>>>>>> // p3 - end point
>>>>>>>> // segs - number of segments
>>>>>>>> function bez(p0, p1, p2, p3, segs) = [
>>>>>>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>>>>>>> ];
>>>>>>>>
>>>>>>>> It is that final function bez() that I actually call, e.g.
>>>>>>>>
>>>>>>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>>>>>>
>>>>>>>> often concatenating the results of several bez() calls together.
>>>>>>>>
>>>>>>>> Note that the four coordinates correspond to the coordinates of the
>>>>>>>> control points in a GUI drawing program: the start point, control point
>>>>>>>> associated with the start, the control point associated with the end, and
>>>>>>>> the end point. I have sometimes created OpenSCAD objects by tracing an
>>>>>>>> object in a drawing program and then reading off the coordinates of the
>>>>>>>> various control points.
>>>>>>>>
>>>>>>>>
>>>>>>>> Note that Bézier functions are not the only mathematical curves.
>>>>>>>> (For instance, they cannot exactly match an arc of a circle.) I'm sure
>>>>>>>> there are numerous other functions that also produce curves.
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>


NH
nop head
Fri, Aug 5, 2022 10:32 PM
A long discussion but I have to ask why do you need an elliptical polygon
with equal tangential sides?
On Fri, 5 Aug 2022, 21:58 Adrian Mariano, avm4@cornell.edu wrote:
You think that a circumscribing polygon with equal length segments does
not exist?? I'm skeptical of this claim.
For circumscribed, it's not so hard. You start with a uniform-in-angle
point distribution, compute the segment lengths, compare to the mean
segment length to get an error, and then compute an adjustment based on the
error. It converges quickly.
So for example, I have segments lengths of:
ECHO: [5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297,
5.57297]
Maybe not exactly equal, since tolerance is 1e-9, but surely good enough.
[image: image.png]
The code for this is in BOSL2 in shapes2d.scad. A similar algorithm should
exist for the circumscribed case, but as I said, my efforts to find it have
failed.
On Fri, Aug 5, 2022 at 12:44 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I think circumscribed polygon segments cannot be equal lengths.
inscribed ones may be approximately equal, but would be a very tough
problem to solve.
I tried something.
On Thu, 4 Aug 2022 at 05:44, Adrian Mariano avm4@cornell.edu wrote:
I think you need to be a little careful about defining what you want to
do. If you want to approximate an ellipse with points that are distributed
uniformly over the ellipse, that could be done by approximating the arc
length of the ellipse to find the necessary points---e.g. advance distance
d along the ellipse at each step. But if you want to approximate an
ellipse with a polygon with equal length sides, that approach does not do
it, because the length of the segments will not be constant as the span
sections of the ellipse with differing curvature. And since the perimeter
of the desired polygon is unknown, you can't just step it out analogously.
The circle doesn't present this challenge due to having constant
curvature.
On Wed, Aug 3, 2022 at 7:41 PM Father Horton fatherhorton@gmail.com
wrote:
I think our emails crossed. I was addressing how to approximate an
ellipse with constant-length segments in general, not how to solve your
problem. When I had to do something similar, I used polar coordinates and
stepped up the value of theta until the distance from the previous point
was correct. (In the constant-length version, I'd keep a running total of
the maximum desired length so that round-off errors don't accumulate.)
Figuring out the circumscribed polygon is, as you note, a greater
challenge. I can visualize how to do it for n = 4, but it doesn't
extrapolate at all.
On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano avm4@cornell.edu
wrote:
Eh, there's no such thing as "brute force" in this situation. Step
through what with sufficiently small steps? Of course an iterative
algorithm is necessary. This is true for most interesting problems. No
big deal. Show me an iterative algorithm that converges to the
circumscribing polygon. When I tried to devise such an algorithm I
couldn't find one that would converge. Writing an algorithm that would
converge to the inscribed polygon seemed to be straight forward. Note
also that computing arc length of the ellipse doesn't really help here.
You can do that by solving an elliptical integral, or summing up small
segments. But what's the connection between arc length of the ellipse and
a circumscribing polygon with equal segment lengths? If there's a
connection, I don't see it.
On Tue, Aug 2, 2022 at 10:56 PM Father Horton fatherhorton@gmail.com
wrote:
Except by brute force (step through it with sufficiently small
steps), it’s not possible because there’s no closed form expression for the
distance between two points on a general ellipse (as opposed to special
cases like a circle).
On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano avm4@cornell.edu
wrote:
Here's a challenge for you: draw an "ellipse" polygon with N
segments that are all the same length that circumscribes a perfect ellipse
with given semiaxes a and b. I tried to solve this problem and could not
find a solution. I can draw an inscribed N segment "ellipse" polygon
with all segments the same length---though it's not easy---but the
circumscribed case eludes me. I think of the inscribed case as, every
vertex is located on the ellipse and the circumscribed case, every segment
is tangent to the ellipse
On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In openscad drawing a ellipse is not too difficult
Refer following code
function to draw an ellipse with semi-major and semi-minor axis
"r1" and "r2" respectively and with center "cp" and number of segment "s"
/
// example:
// sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
function ellipse(r1,r2,cp,s=30)=
let(
sec=[for(i=[0:360/s:360-360/s])cp+[r1cos(i),r2sin(i)]]
)sec;
On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
openscad@jordan.maileater.net> wrote:
On 8/2/2022 4:46 PM, Brian Allen wrote:
I created an oval using:
inMm = 25.4;
fullW = 35.5 * inMm;
fullL = 54.5 * inMm;
resize([fullW, fullL, 1])
circle(d=fullW);
Tip: use scale() rather than resize(); it previews faster in
complicated cases.
It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
You're taking a circle and stretching it; the result of that
stretching is an ellipse.
I'm not 100% sure - maybe one of the real math wizards can chime
in - but I think the shape you are asking for would not be an ellipse.
I believe that an ellipse is fully defined by its major (long) and
minor (short) axis dimensions; the other parts of the curve mathematically
flow from those two measurements.
You can make something else, but you can't make it using this
technique.
Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
You can use a Bézier function.
Using BOSL2:
https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
DIY, here's a function that I cobbled together some years ago:
// Bezier functions from https://www.thingiverse.com/thing:8443
// but that yielded either single points or a raft of triangles;
// this yields a vector of points that you can then concatenate
// with other pieces to form a single polygon.
// If we were really clever, I think it would be possible to
// automatically space the output points based on how linear
// the curve is at that point. But right now I'm not that clever.
function BEZ03(u) = pow((1-u), 3);
function BEZ13(u) = 3u(pow((1-u),2));
function BEZ23(u) = 3*(pow(u,2))*(1-u);
function BEZ33(u) = pow(u,3);
function PointAlongBez4(p0, p1, p2, p3, u) = [
BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
// p0 - start point
// p1 - control point 1, line departs p0 headed this way
// p2 - control point 2, line arrives at p3 from this way
// p3 - end point
// segs - number of segments
function bez(p0, p1, p2, p3, segs) = [
for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
];
It is that final function bez() that I actually call, e.g.
polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
often concatenating the results of several bez() calls together.
Note that the four coordinates correspond to the coordinates of
the control points in a GUI drawing program: the start point, control
point associated with the start, the control point associated with the end,
and the end point. I have sometimes created OpenSCAD objects by tracing an
object in a drawing program and then reading off the coordinates of the
various control points.
Note that Bézier functions are not the only mathematical curves.
(For instance, they cannot exactly match an arc of a circle.) I'm sure
there are numerous other functions that also produce curves.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
A long discussion but I have to ask why do you need an elliptical polygon
with equal tangential sides?
On Fri, 5 Aug 2022, 21:58 Adrian Mariano, <avm4@cornell.edu> wrote:
> You think that a circumscribing polygon with equal length segments does
> not exist?? I'm skeptical of this claim.
>
> For circumscribed, it's not so hard. You start with a uniform-in-angle
> point distribution, compute the segment lengths, compare to the mean
> segment length to get an error, and then compute an adjustment based on the
> error. It converges quickly.
>
> So for example, I have segments lengths of:
>
> ECHO: [5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297, 5.57297,
> 5.57297]
>
> Maybe not exactly equal, since tolerance is 1e-9, but surely good enough.
> [image: image.png]
>
> The code for this is in BOSL2 in shapes2d.scad. A similar algorithm should
> exist for the circumscribed case, but as I said, my efforts to find it have
> failed.
>
> On Fri, Aug 5, 2022 at 12:44 PM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> I think circumscribed polygon segments cannot be equal lengths.
>> inscribed ones may be approximately equal, but would be a very tough
>> problem to solve.
>> I tried something.
>>
>>
>>
>> On Thu, 4 Aug 2022 at 05:44, Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> I think you need to be a little careful about defining what you want to
>>> do. If you want to approximate an ellipse with points that are distributed
>>> uniformly over the ellipse, that could be done by approximating the arc
>>> length of the ellipse to find the necessary points---e.g. advance distance
>>> d along the ellipse at each step. But if you want to approximate an
>>> ellipse with a polygon with equal length sides, that approach does not do
>>> it, because the length of the segments will not be constant as the span
>>> sections of the ellipse with differing curvature. And since the perimeter
>>> of the desired polygon is unknown, you can't just step it out analogously.
>>> The circle doesn't present this challenge due to having constant
>>> curvature.
>>>
>>> On Wed, Aug 3, 2022 at 7:41 PM Father Horton <fatherhorton@gmail.com>
>>> wrote:
>>>
>>>> I think our emails crossed. I was addressing how to approximate an
>>>> ellipse with constant-length segments in general, not how to solve your
>>>> problem. When I had to do something similar, I used polar coordinates and
>>>> stepped up the value of theta until the distance from the previous point
>>>> was correct. (In the constant-length version, I'd keep a running total of
>>>> the maximum desired length so that round-off errors don't accumulate.)
>>>>
>>>> Figuring out the circumscribed polygon is, as you note, a greater
>>>> challenge. I can visualize how to do it for n = 4, but it doesn't
>>>> extrapolate at all.
>>>>
>>>> On Tue, Aug 2, 2022 at 10:10 PM Adrian Mariano <avm4@cornell.edu>
>>>> wrote:
>>>>
>>>>> Eh, there's no such thing as "brute force" in this situation. Step
>>>>> through *what* with sufficiently small steps? Of course an iterative
>>>>> algorithm is necessary. This is true for most interesting problems. No
>>>>> big deal. Show me an iterative algorithm that converges to the
>>>>> circumscribing polygon. When I tried to devise such an algorithm I
>>>>> couldn't find one that would converge. Writing an algorithm that would
>>>>> converge to the *inscribed* polygon seemed to be straight forward. Note
>>>>> also that computing arc length of the ellipse doesn't really help here.
>>>>> You can do that by solving an elliptical integral, or summing up small
>>>>> segments. But what's the connection between arc length of the ellipse and
>>>>> a circumscribing polygon with equal segment lengths? If there's a
>>>>> connection, I don't see it.
>>>>>
>>>>> On Tue, Aug 2, 2022 at 10:56 PM Father Horton <fatherhorton@gmail.com>
>>>>> wrote:
>>>>>
>>>>>> Except by brute force (step through it with sufficiently small
>>>>>> steps), it’s not possible because there’s no closed form expression for the
>>>>>> distance between two points on a general ellipse (as opposed to special
>>>>>> cases like a circle).
>>>>>>
>>>>>> On Tue, Aug 2, 2022 at 9:50 PM Adrian Mariano <avm4@cornell.edu>
>>>>>> wrote:
>>>>>>
>>>>>>> Here's a challenge for you: draw an "ellipse" polygon with N
>>>>>>> segments that are all the same length that circumscribes a perfect ellipse
>>>>>>> with given semiaxes a and b. I tried to solve this problem and could not
>>>>>>> find a solution. I can draw an *inscribed* N segment "ellipse" polygon
>>>>>>> with all segments the same length---though it's not easy---but the
>>>>>>> circumscribed case eludes me. I think of the inscribed case as, every
>>>>>>> vertex is located on the ellipse and the circumscribed case, every segment
>>>>>>> is tangent to the ellipse
>>>>>>>
>>>>>>> On Tue, Aug 2, 2022 at 10:36 PM Sanjeev Prabhakar <
>>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>>
>>>>>>>> In openscad drawing a ellipse is not too difficult
>>>>>>>> Refer following code
>>>>>>>>
>>>>>>>> function to draw an ellipse with semi-major and semi-minor axis
>>>>>>>> "r1" and "r2" respectively and with center "cp" and number of segment "s"
>>>>>>>> /
>>>>>>>> // example:
>>>>>>>> // sec=ellipse(r1=5,r2=3,cp=[2,3],s=30);
>>>>>>>>
>>>>>>>> function ellipse(r1,r2,cp,s=30)=
>>>>>>>> let(
>>>>>>>> sec=[for(i=[0:360/s:360-360/s])cp+[r1*cos(i),r2*sin(i)]]
>>>>>>>> )sec;
>>>>>>>>
>>>>>>>> On Wed, 3 Aug, 2022, 5:35 am Jordan Brown, <
>>>>>>>> openscad@jordan.maileater.net> wrote:
>>>>>>>>
>>>>>>>>> On 8/2/2022 4:46 PM, Brian Allen wrote:
>>>>>>>>>
>>>>>>>>> I created an oval using:
>>>>>>>>> inMm = 25.4;
>>>>>>>>> fullW = 35.5 * inMm;
>>>>>>>>> fullL = 54.5 * inMm;
>>>>>>>>> resize([fullW, fullL, 1])
>>>>>>>>> circle(d=fullW);
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> Tip: use scale() rather than resize(); it previews faster in
>>>>>>>>> complicated cases.
>>>>>>>>>
>>>>>>>>> It's the right size in the middle (35.5" wide at 50% of the length), but 25% along the length it's not quite as wide as I need it (it's 31.5" and I need it about 32"). If you can see the attached image I'm trying to make the yellow oval match the red "sanity check" lines. I'm trying to match the size and shape of an existing oval in the real world.
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> You're taking a circle and stretching it; the result of that
>>>>>>>>> stretching is an ellipse.
>>>>>>>>>
>>>>>>>>> I'm not 100% sure - maybe one of the real math wizards can chime
>>>>>>>>> in - but I think the shape you are asking for would not be an ellipse.
>>>>>>>>>
>>>>>>>>> I believe that an ellipse is fully defined by its major (long) and
>>>>>>>>> minor (short) axis dimensions; the other parts of the curve mathematically
>>>>>>>>> flow from those two measurements.
>>>>>>>>>
>>>>>>>>> You can make something else, but you can't make it using this
>>>>>>>>> technique.
>>>>>>>>>
>>>>>>>>> Is there a way to stretch this in OpenSCAD? In a GUI vector graphics program I'd use a bézier curve and drag the handle to get 1/4 of it just right then mirror it in X and Y to get the oval I needed.
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> You can use a Bézier function.
>>>>>>>>>
>>>>>>>>> Using BOSL2:
>>>>>>>>> https://github.com/revarbat/BOSL2/wiki/Topics#bezier-curves
>>>>>>>>>
>>>>>>>>> DIY, here's a function that I cobbled together some years ago:
>>>>>>>>>
>>>>>>>>> // Bezier functions from https://www.thingiverse.com/thing:8443
>>>>>>>>> // but that yielded either single points or a raft of triangles;
>>>>>>>>> // this yields a vector of points that you can then concatenate
>>>>>>>>> // with other pieces to form a single polygon.
>>>>>>>>> // If we were really clever, I think it would be possible to
>>>>>>>>> // automatically space the output points based on how linear
>>>>>>>>> // the curve is at that point. But right now I'm not that clever.
>>>>>>>>> function BEZ03(u) = pow((1-u), 3);
>>>>>>>>> function BEZ13(u) = 3*u*(pow((1-u),2));
>>>>>>>>> function BEZ23(u) = 3*(pow(u,2))*(1-u);
>>>>>>>>> function BEZ33(u) = pow(u,3);
>>>>>>>>>
>>>>>>>>> function PointAlongBez4(p0, p1, p2, p3, u) = [
>>>>>>>>> BEZ03(u)*p0[0]+BEZ13(u)*p1[0]+BEZ23(u)*p2[0]+BEZ33(u)*p3[0],
>>>>>>>>> BEZ03(u)*p0[1]+BEZ13(u)*p1[1]+BEZ23(u)*p2[1]+BEZ33(u)*p3[1]];
>>>>>>>>>
>>>>>>>>> // p0 - start point
>>>>>>>>> // p1 - control point 1, line departs p0 headed this way
>>>>>>>>> // p2 - control point 2, line arrives at p3 from this way
>>>>>>>>> // p3 - end point
>>>>>>>>> // segs - number of segments
>>>>>>>>> function bez(p0, p1, p2, p3, segs) = [
>>>>>>>>> for (i = [0:segs]) PointAlongBez4(p0, p1, p2, p3, i/segs)
>>>>>>>>> ];
>>>>>>>>>
>>>>>>>>> It is that final function bez() that I actually call, e.g.
>>>>>>>>>
>>>>>>>>> polygon(bez([0,0], [0,4], [5,1], [7,0], 20));
>>>>>>>>>
>>>>>>>>> often concatenating the results of several bez() calls together.
>>>>>>>>>
>>>>>>>>> Note that the four coordinates correspond to the coordinates of
>>>>>>>>> the control points in a GUI drawing program: the start point, control
>>>>>>>>> point associated with the start, the control point associated with the end,
>>>>>>>>> and the end point. I have sometimes created OpenSCAD objects by tracing an
>>>>>>>>> object in a drawing program and then reading off the coordinates of the
>>>>>>>>> various control points.
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> Note that Bézier functions are not the only mathematical curves.
>>>>>>>>> (For instance, they cannot exactly match an arc of a circle.) I'm sure
>>>>>>>>> there are numerous other functions that also produce curves.
>>>>>>>>> _______________________________________________
>>>>>>>>> OpenSCAD mailing list
>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>






