SP
Sanjeev Prabhakar
Sun, Sep 3, 2023 1:32 PM
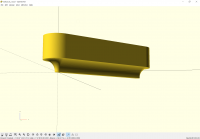
I have observed the offset function I wrote in openscad was much slower
than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the methods
seem to be almost equally efficient or inefficient, whatever way you want
to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu wrote:
I think that Sanjeev has identified the two main approaches. You can make
a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded rectangle
which avoids issues with self-intersection of the sweep. This is probably
the best way to do this in terms of efficiency. Note also that using
turtle() to compute a rounded rectangle is overkill. I only use turtle()
for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible using
offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside directly
and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(), again
with a difference. However, rounded_prism doesn't make circular roundings,
so the results will be a bit different, and it will not be possible to
assure a uniform width at the corners. (Roundovers here are continuous
curvature beziers. The k parameter controls how gentle the transition,
with a value of .8 close to circular. Smaller k values will give gentler
transitions, but then large joint distance may be desired. Try changing k
to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is not
so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those points??
I had to hollow out the part a bit and change the shape some so I would
like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
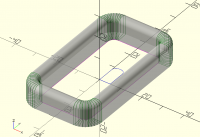
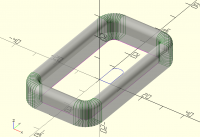
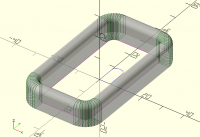
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
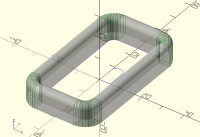
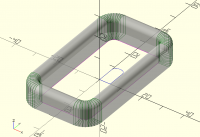
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside edges
to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I have observed the offset function I wrote in openscad was much slower
than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the methods
seem to be almost equally efficient or inefficient, whatever way you want
to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu> wrote:
> I think that Sanjeev has identified the two main approaches. You can make
> a rounded rectangle shape and sweep. That would look like this:
>
> include<BOSL2/std.scad>
>
> $fa=1;$fs=1;
> W=34;L=60;H=10;Or = 8;Ir = 3;
>
> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
> path = rect([W,L],rounding=Ir);
> path_sweep(section,path,closed=true);
>
> Note that I have chosen as the sweep path the inner rounded rectangle
> which avoids issues with self-intersection of the sweep. This is probably
> the best way to do this in terms of efficiency. Note also that using
> turtle() to compute a rounded rectangle is overkill. I only use turtle()
> for shapes that are somehow irregular.
>
> Sanjeev's second approach is to use offsetting. This is possible using
> offset_sweep(), but will likely be slower than path_sweep() because
> computing offset in userspace is slow. To do this, you have to compute the
> outside rounded shape and then subtract the inner rounded shape. So it
> could be done like this:
>
> include<BOSL2/std.scad>
> include<BOSL2/rounding.scad>
>
> $fa=1;$fs=1;
> W=34;L=60;H=10;Or = 8;Ir = 3;
>
> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
> outside = rect([W,L], rounding=Or);
>
> difference(){
> offset_sweep(outside, h=H, top=os_circle(r=2));
> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
> }
>
> Note that you could also compute just one of inside and outside directly
> and get the other one with offset().
>
> A third way to make a shape like this is to use rounded_prism(), again
> with a difference. However, rounded_prism doesn't make circular roundings,
> so the results will be a bit different, and it will not be possible to
> assure a uniform width at the corners. (Roundovers here are continuous
> curvature beziers. The k parameter controls how gentle the transition,
> with a value of .8 close to circular. Smaller k values will give gentler
> transitions, but then large joint distance may be desired. Try changing k
> to 0.5 to see the difference.)
>
> include<BOSL2/std.scad>
> include<BOSL2/rounding.scad>
>
> $fa=1;$fs=1;
> W=34;L=60;H=10;Or = 8;Ir = 3;
>
> diff(){
> rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
> joint_top=-2, joint_sides=6,k=.8);
> }
>
>
> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> I will explain the process
>> I think this is important.
>>
>> There are 2 approaches.
>> 1. Extrude a section along a path
>> 2. Make a section and offset it multiple times to generate a solid.
>>
>> I am sure this explanation is not enough. Will create a visual
>> description and send it to you.
>>
>> For approach 2:
>> The key is writing a function to offset a section, which I think is not
>> so easy.
>>
>>
>>
>>
>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com> wrote:
>>
>>> Hi Sanjeev,
>>>
>>>
>>> Thank you. It's beautiful, but how did you generate all those points??
>>>
>>>
>>> I had to hollow out the part a bit and change the shape some so I would
>>> like to find a more generic way to round the edges.
>>>
>>>
>>>
>>> Bob
>>>
>>>
>>>
>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>
>>> attached file
>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>
>>>
>>>
>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com> wrote:
>>>
>>>> Hello OpenSCAD,
>>>>
>>>> I want the bottom to be straight and the top inside and outside edges
>>>> to have 2mm roundover
>>>>
>>>> Thank you.
>>>>
>>>> include <BOSL2/std.scad> //or screws or threading
>>>>
>>>> W=34;
>>>> L=60;
>>>> H=10;
>>>> Or = 8;
>>>> Ir = 3;
>>>>
>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>
>>>> --
>>>> Best regards,
>>>> Bob mailto:roosbob@wybatap.com
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>>
>>> --
>>> have Fun,
>>> Bob mailto:roosbob@wybatap.com
>>> <roosbob@wybatap.com>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

WF
William F. Adams
Sun, Sep 3, 2023 1:37 PM
I actually managed to do this using the library I've been working on for mimicking G-code cutting on CNC machines:
https://github.com/WillAdams/gcodepreview
Basically, you define a roundover tool:
https://community.carbide3d.com/t/using-unsupported-tooling-in-carbide-create-roundover-cove-radius-bits/43723
https://community.carbide3d.com/t/previewing-g-code-using-openscad/35153
//!OpenSCAD
Endmill_Diameter = 6.35; Detail = 100;
$fn = Detail * 1;
tool_radius_tip = 0.79375; tool_radius_width = 3.175;
feedrate = 600; plungerate = 150; safeheight = 8;
module radiuscut(bx, by, bz, ex, ey, ez) { n = Detail; step = 360/n; endmillradius = Endmill_Diameter / 2; hull(){ translate([bx,by,bz]) cylinder(step,tool_radius_tip,tool_radius_tip); translate([ex,ey,ez]) cylinder(step,tool_radius_tip,tool_radius_tip); }
hull(){ translate([bx,by,bz+tool_radius_width]) cylinder(tool_radius_width2,tool_radius_tip+tool_radius_width,tool_radius_tip+tool_radius_width); translate([ex,ey,ez+tool_radius_width]) cylinder(tool_radius_width2,tool_radius_tip+tool_radius_width,tool_radius_tip+tool_radius_wi dth); } for (i=[0:step:90]) { angle = i; dx = tool_radius_widthcos(angle); dxx = tool_radius_widthcos(angle+step); dzz = tool_radius_widthsin(angle); dz = tool_radius_widthsin(angle+step); dh = dz-dzz; hull(){ translate([bx,by,bz+dz]) cylinder(dh,tool_radius_tip+tool_radius_width-dx,tool_radius_tip+tool_radius_width-dxx); translate([ex,ey,ez+dz]) cylinder(dh,tool_radius_tip+tool_radius_width-dx,tool_radius_tip+tool_radius_width-dxx); } } }
radiuscut(0, 0, 0, 20, 20, 0);
which previews as:
https://community.carbide3d.com/uploads/default/original/3X/5/4/540b04fcd2dbfebb78c08a748ff980aa3238c8e2.png
and then you subtract that from the design which you are modeling.
William
I actually managed to do this using the library I've been working on for mimicking G-code cutting on CNC machines:
https://github.com/WillAdams/gcodepreview
Basically, you define a roundover tool:
https://community.carbide3d.com/t/using-unsupported-tooling-in-carbide-create-roundover-cove-radius-bits/43723
https://community.carbide3d.com/t/previewing-g-code-using-openscad/35153
//!OpenSCAD
Endmill_Diameter = 6.35; Detail = 100;
$fn = Detail * 1;
tool_radius_tip = 0.79375; tool_radius_width = 3.175;
feedrate = 600; plungerate = 150; safeheight = 8;
module radiuscut(bx, by, bz, ex, ey, ez) { n = Detail; step = 360/n; endmillradius = Endmill_Diameter / 2; hull(){ translate([bx,by,bz]) cylinder(step,tool_radius_tip,tool_radius_tip); translate([ex,ey,ez]) cylinder(step,tool_radius_tip,tool_radius_tip); }
hull(){ translate([bx,by,bz+tool_radius_width]) cylinder(tool_radius_width*2,tool_radius_tip+tool_radius_width,tool_radius_tip+tool_radius_width); translate([ex,ey,ez+tool_radius_width]) cylinder(tool_radius_width*2,tool_radius_tip+tool_radius_width,tool_radius_tip+tool_radius_wi dth); } for (i=[0:step:90]) { angle = i; dx = tool_radius_width*cos(angle); dxx = tool_radius_width*cos(angle+step); dzz = tool_radius_width*sin(angle); dz = tool_radius_width*sin(angle+step); dh = dz-dzz; hull(){ translate([bx,by,bz+dz]) cylinder(dh,tool_radius_tip+tool_radius_width-dx,tool_radius_tip+tool_radius_width-dxx); translate([ex,ey,ez+dz]) cylinder(dh,tool_radius_tip+tool_radius_width-dx,tool_radius_tip+tool_radius_width-dxx); } } }
radiuscut(0, 0, 0, 20, 20, 0);
which previews as:
https://community.carbide3d.com/uploads/default/original/3X/5/4/540b04fcd2dbfebb78c08a748ff980aa3238c8e2.png
and then you subtract that from the design which you are modeling.
William

AM
Adrian Mariano
Sun, Sep 3, 2023 1:47 PM
Sanjeev, I don't know how you implemented offset, either in python or in
OpenSCAD, but the problem I have is that checking for invalid portions of
the path after doing the basic offset becomes a quadratic run time task in
OpenSCAD. In other languages, it is possible to use clever data structures
and I think do it in N log N. I saw an algorithm for offset that involves
doing the basic offset and then keeping only the parts of the result that
meet a criterion based on winding number, but the computation to partition
the path into its regions and compute the winding number is very slow in
OpenSCAD, again because without data structures, everything has at least
quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I have observed the offset function I wrote in openscad was much slower
than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the methods
seem to be almost equally efficient or inefficient, whatever way you want
to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu wrote:
I think that Sanjeev has identified the two main approaches. You can
make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded rectangle
which avoids issues with self-intersection of the sweep. This is probably
the best way to do this in terms of efficiency. Note also that using
turtle() to compute a rounded rectangle is overkill. I only use turtle()
for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible using
offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside directly
and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(), again
with a difference. However, rounded_prism doesn't make circular roundings,
so the results will be a bit different, and it will not be possible to
assure a uniform width at the corners. (Roundovers here are continuous
curvature beziers. The k parameter controls how gentle the transition,
with a value of .8 close to circular. Smaller k values will give gentler
transitions, but then large joint distance may be desired. Try changing k
to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is not
so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those points??
I had to hollow out the part a bit and change the shape some so I would
like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside edges
to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Sanjeev, I don't know how you implemented offset, either in python or in
OpenSCAD, but the problem I have is that checking for invalid portions of
the path after doing the basic offset becomes a quadratic run time task in
OpenSCAD. In other languages, it is possible to use clever data structures
and I think do it in N log N. I saw an algorithm for offset that involves
doing the basic offset and then keeping only the parts of the result that
meet a criterion based on winding number, but the computation to partition
the path into its regions and compute the winding number is very slow in
OpenSCAD, again because without data structures, everything has at least
quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I have observed the offset function I wrote in openscad was much slower
> than the offset function written in python.
>
> Maybe the numpy has a lot of support and is faster. So both the methods
> seem to be almost equally efficient or inefficient, whatever way you want
> to look at it.
>
> also missed to share that the skeleton of the path extrude method is
> different from the offset method.
>
> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>
> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> I think that Sanjeev has identified the two main approaches. You can
>> make a rounded rectangle shape and sweep. That would look like this:
>>
>> include<BOSL2/std.scad>
>>
>> $fa=1;$fs=1;
>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>
>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>> path = rect([W,L],rounding=Ir);
>> path_sweep(section,path,closed=true);
>>
>> Note that I have chosen as the sweep path the inner rounded rectangle
>> which avoids issues with self-intersection of the sweep. This is probably
>> the best way to do this in terms of efficiency. Note also that using
>> turtle() to compute a rounded rectangle is overkill. I only use turtle()
>> for shapes that are somehow irregular.
>>
>> Sanjeev's second approach is to use offsetting. This is possible using
>> offset_sweep(), but will likely be slower than path_sweep() because
>> computing offset in userspace is slow. To do this, you have to compute the
>> outside rounded shape and then subtract the inner rounded shape. So it
>> could be done like this:
>>
>> include<BOSL2/std.scad>
>> include<BOSL2/rounding.scad>
>>
>> $fa=1;$fs=1;
>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>
>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>> outside = rect([W,L], rounding=Or);
>>
>> difference(){
>> offset_sweep(outside, h=H, top=os_circle(r=2));
>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>> }
>>
>> Note that you could also compute just one of inside and outside directly
>> and get the other one with offset().
>>
>> A third way to make a shape like this is to use rounded_prism(), again
>> with a difference. However, rounded_prism doesn't make circular roundings,
>> so the results will be a bit different, and it will not be possible to
>> assure a uniform width at the corners. (Roundovers here are continuous
>> curvature beziers. The k parameter controls how gentle the transition,
>> with a value of .8 close to circular. Smaller k values will give gentler
>> transitions, but then large joint distance may be desired. Try changing k
>> to 0.5 to see the difference.)
>>
>> include<BOSL2/std.scad>
>> include<BOSL2/rounding.scad>
>>
>> $fa=1;$fs=1;
>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>
>> diff(){
>> rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
>>
>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>> joint_top=-2, joint_sides=6,k=.8);
>> }
>>
>>
>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> I will explain the process
>>> I think this is important.
>>>
>>> There are 2 approaches.
>>> 1. Extrude a section along a path
>>> 2. Make a section and offset it multiple times to generate a solid.
>>>
>>> I am sure this explanation is not enough. Will create a visual
>>> description and send it to you.
>>>
>>> For approach 2:
>>> The key is writing a function to offset a section, which I think is not
>>> so easy.
>>>
>>>
>>>
>>>
>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com> wrote:
>>>
>>>> Hi Sanjeev,
>>>>
>>>>
>>>> Thank you. It's beautiful, but how did you generate all those points??
>>>>
>>>>
>>>> I had to hollow out the part a bit and change the shape some so I would
>>>> like to find a more generic way to round the edges.
>>>>
>>>>
>>>>
>>>> Bob
>>>>
>>>>
>>>>
>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>
>>>> attached file
>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>
>>>>
>>>>
>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com> wrote:
>>>>
>>>>> Hello OpenSCAD,
>>>>>
>>>>> I want the bottom to be straight and the top inside and outside edges
>>>>> to have 2mm roundover
>>>>>
>>>>> Thank you.
>>>>>
>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>
>>>>> W=34;
>>>>> L=60;
>>>>> H=10;
>>>>> Or = 8;
>>>>> Ir = 3;
>>>>>
>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>
>>>>> --
>>>>> Best regards,
>>>>> Bob mailto:roosbob@wybatap.com
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>>
>>>> --
>>>> have Fun,
>>>> Bob mailto:roosbob@wybatap.com
>>>> <roosbob@wybatap.com>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Sun, Sep 3, 2023 2:13 PM
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original section such
that the radius of the round is equal to offset required minus some very
small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I don't know how you implemented offset, either in python or in
OpenSCAD, but the problem I have is that checking for invalid portions of
the path after doing the basic offset becomes a quadratic run time task in
OpenSCAD. In other languages, it is possible to use clever data structures
and I think do it in N log N. I saw an algorithm for offset that involves
doing the basic offset and then keeping only the parts of the result that
meet a criterion based on winding number, but the computation to partition
the path into its regions and compute the winding number is very slow in
OpenSCAD, again because without data structures, everything has at least
quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I have observed the offset function I wrote in openscad was much slower
than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the methods
seem to be almost equally efficient or inefficient, whatever way you want
to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu wrote:
I think that Sanjeev has identified the two main approaches. You can
make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded rectangle
which avoids issues with self-intersection of the sweep. This is probably
the best way to do this in terms of efficiency. Note also that using
turtle() to compute a rounded rectangle is overkill. I only use turtle()
for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible using
offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside directly
and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(), again
with a difference. However, rounded_prism doesn't make circular roundings,
so the results will be a bit different, and it will not be possible to
assure a uniform width at the corners. (Roundovers here are continuous
curvature beziers. The k parameter controls how gentle the transition,
with a value of .8 close to circular. Smaller k values will give gentler
transitions, but then large joint distance may be desired. Try changing k
to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is not
so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those points??
I had to hollow out the part a bit and change the shape some so I
would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside edges
to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
1. Original section is divided in to line segments.
2. Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
3. There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
4. All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
5. create a rounded shape around each segment of the original section such
that the radius of the round is equal to offset required minus some very
small value like 0.001.
6. Now check if any point is inside these rounded shapes and discard it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu> wrote:
> Sanjeev, I don't know how you implemented offset, either in python or in
> OpenSCAD, but the problem I have is that checking for invalid portions of
> the path after doing the basic offset becomes a quadratic run time task in
> OpenSCAD. In other languages, it is possible to use clever data structures
> and I think do it in N log N. I saw an algorithm for offset that involves
> doing the basic offset and then keeping only the parts of the result that
> meet a criterion based on winding number, but the computation to partition
> the path into its regions and compute the winding number is very slow in
> OpenSCAD, again because without data structures, everything has at least
> quadratic run time.
>
> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> I have observed the offset function I wrote in openscad was much slower
>> than the offset function written in python.
>>
>> Maybe the numpy has a lot of support and is faster. So both the methods
>> seem to be almost equally efficient or inefficient, whatever way you want
>> to look at it.
>>
>> also missed to share that the skeleton of the path extrude method is
>> different from the offset method.
>>
>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>
>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> I think that Sanjeev has identified the two main approaches. You can
>>> make a rounded rectangle shape and sweep. That would look like this:
>>>
>>> include<BOSL2/std.scad>
>>>
>>> $fa=1;$fs=1;
>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>
>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>> path = rect([W,L],rounding=Ir);
>>> path_sweep(section,path,closed=true);
>>>
>>> Note that I have chosen as the sweep path the inner rounded rectangle
>>> which avoids issues with self-intersection of the sweep. This is probably
>>> the best way to do this in terms of efficiency. Note also that using
>>> turtle() to compute a rounded rectangle is overkill. I only use turtle()
>>> for shapes that are somehow irregular.
>>>
>>> Sanjeev's second approach is to use offsetting. This is possible using
>>> offset_sweep(), but will likely be slower than path_sweep() because
>>> computing offset in userspace is slow. To do this, you have to compute the
>>> outside rounded shape and then subtract the inner rounded shape. So it
>>> could be done like this:
>>>
>>> include<BOSL2/std.scad>
>>> include<BOSL2/rounding.scad>
>>>
>>> $fa=1;$fs=1;
>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>
>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>> outside = rect([W,L], rounding=Or);
>>>
>>> difference(){
>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>> }
>>>
>>> Note that you could also compute just one of inside and outside directly
>>> and get the other one with offset().
>>>
>>> A third way to make a shape like this is to use rounded_prism(), again
>>> with a difference. However, rounded_prism doesn't make circular roundings,
>>> so the results will be a bit different, and it will not be possible to
>>> assure a uniform width at the corners. (Roundovers here are continuous
>>> curvature beziers. The k parameter controls how gentle the transition,
>>> with a value of .8 close to circular. Smaller k values will give gentler
>>> transitions, but then large joint distance may be desired. Try changing k
>>> to 0.5 to see the difference.)
>>>
>>> include<BOSL2/std.scad>
>>> include<BOSL2/rounding.scad>
>>>
>>> $fa=1;$fs=1;
>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>
>>> diff(){
>>> rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
>>>
>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>> joint_top=-2, joint_sides=6,k=.8);
>>> }
>>>
>>>
>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> I will explain the process
>>>> I think this is important.
>>>>
>>>> There are 2 approaches.
>>>> 1. Extrude a section along a path
>>>> 2. Make a section and offset it multiple times to generate a solid.
>>>>
>>>> I am sure this explanation is not enough. Will create a visual
>>>> description and send it to you.
>>>>
>>>> For approach 2:
>>>> The key is writing a function to offset a section, which I think is not
>>>> so easy.
>>>>
>>>>
>>>>
>>>>
>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com> wrote:
>>>>
>>>>> Hi Sanjeev,
>>>>>
>>>>>
>>>>> Thank you. It's beautiful, but how did you generate all those points??
>>>>>
>>>>>
>>>>> I had to hollow out the part a bit and change the shape some so I
>>>>> would like to find a more generic way to round the edges.
>>>>>
>>>>>
>>>>>
>>>>> Bob
>>>>>
>>>>>
>>>>>
>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>
>>>>> attached file
>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>
>>>>>
>>>>>
>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com> wrote:
>>>>>
>>>>>> Hello OpenSCAD,
>>>>>>
>>>>>> I want the bottom to be straight and the top inside and outside edges
>>>>>> to have 2mm roundover
>>>>>>
>>>>>> Thank you.
>>>>>>
>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>
>>>>>> W=34;
>>>>>> L=60;
>>>>>> H=10;
>>>>>> Or = 8;
>>>>>> Ir = 3;
>>>>>>
>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>
>>>>>> --
>>>>>> Best regards,
>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>>
>>>>> --
>>>>> have Fun,
>>>>> Bob mailto:roosbob@wybatap.com
>>>>> <roosbob@wybatap.com>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Sun, Sep 3, 2023 4:42 PM
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step you
write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is quite
elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original section
such that the radius of the round is equal to offset required minus some
very small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I don't know how you implemented offset, either in python or in
OpenSCAD, but the problem I have is that checking for invalid portions of
the path after doing the basic offset becomes a quadratic run time task in
OpenSCAD. In other languages, it is possible to use clever data structures
and I think do it in N log N. I saw an algorithm for offset that involves
doing the basic offset and then keeping only the parts of the result that
meet a criterion based on winding number, but the computation to partition
the path into its regions and compute the winding number is very slow in
OpenSCAD, again because without data structures, everything has at least
quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have observed the offset function I wrote in openscad was much slower
than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the methods
seem to be almost equally efficient or inefficient, whatever way you want
to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu wrote:
I think that Sanjeev has identified the two main approaches. You can
make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded rectangle
which avoids issues with self-intersection of the sweep. This is probably
the best way to do this in terms of efficiency. Note also that using
turtle() to compute a rounded rectangle is overkill. I only use turtle()
for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible using
offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside
directly and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(), again
with a difference. However, rounded_prism doesn't make circular roundings,
so the results will be a bit different, and it will not be possible to
assure a uniform width at the corners. (Roundovers here are continuous
curvature beziers. The k parameter controls how gentle the transition,
with a value of .8 close to circular. Smaller k values will give gentler
transitions, but then large joint distance may be desired. Try changing k
to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is
not so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those points??
I had to hollow out the part a bit and change the shape some so I
would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside
edges to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step you
write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is quite
elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> It is quadratic for sure.
>
> It needs a separate discussion as per me as this is a complex topic.
>
> If I remember correctly following are the steps
>
> 1. Original section is divided in to line segments.
>
> 2. Each line segment is offset by the amount required and intersection
> between 2 adjacent segments are calculated. In case of concave segments
> there would not be any intersection.
>
> 3. There could be global intersection of segments apart from the
> intersection created in step 2. To calculate this it has to be quadratic.
>
> 4. All the points obtained in step 2 and step 3 to be added in simple
> offset of all the original points.
>
> 5. create a rounded shape around each segment of the original section
> such that the radius of the round is equal to offset required minus some
> very small value like 0.001.
>
> 6. Now check if any point is inside these rounded shapes and discard it.
>
> Balance points needs to be ordered based on the original points .
>
> Now, this seems to be a complicated process, but I think this is the
> simplest way to achieve a offset.
>
>
> On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu> wrote:
>
>> Sanjeev, I don't know how you implemented offset, either in python or in
>> OpenSCAD, but the problem I have is that checking for invalid portions of
>> the path after doing the basic offset becomes a quadratic run time task in
>> OpenSCAD. In other languages, it is possible to use clever data structures
>> and I think do it in N log N. I saw an algorithm for offset that involves
>> doing the basic offset and then keeping only the parts of the result that
>> meet a criterion based on winding number, but the computation to partition
>> the path into its regions and compute the winding number is very slow in
>> OpenSCAD, again because without data structures, everything has at least
>> quadratic run time.
>>
>> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> I have observed the offset function I wrote in openscad was much slower
>>> than the offset function written in python.
>>>
>>> Maybe the numpy has a lot of support and is faster. So both the methods
>>> seem to be almost equally efficient or inefficient, whatever way you want
>>> to look at it.
>>>
>>> also missed to share that the skeleton of the path extrude method is
>>> different from the offset method.
>>>
>>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>>
>>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> I think that Sanjeev has identified the two main approaches. You can
>>>> make a rounded rectangle shape and sweep. That would look like this:
>>>>
>>>> include<BOSL2/std.scad>
>>>>
>>>> $fa=1;$fs=1;
>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>
>>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>>> path = rect([W,L],rounding=Ir);
>>>> path_sweep(section,path,closed=true);
>>>>
>>>> Note that I have chosen as the sweep path the inner rounded rectangle
>>>> which avoids issues with self-intersection of the sweep. This is probably
>>>> the best way to do this in terms of efficiency. Note also that using
>>>> turtle() to compute a rounded rectangle is overkill. I only use turtle()
>>>> for shapes that are somehow irregular.
>>>>
>>>> Sanjeev's second approach is to use offsetting. This is possible using
>>>> offset_sweep(), but will likely be slower than path_sweep() because
>>>> computing offset in userspace is slow. To do this, you have to compute the
>>>> outside rounded shape and then subtract the inner rounded shape. So it
>>>> could be done like this:
>>>>
>>>> include<BOSL2/std.scad>
>>>> include<BOSL2/rounding.scad>
>>>>
>>>> $fa=1;$fs=1;
>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>
>>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>>> outside = rect([W,L], rounding=Or);
>>>>
>>>> difference(){
>>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>>> }
>>>>
>>>> Note that you could also compute just one of inside and outside
>>>> directly and get the other one with offset().
>>>>
>>>> A third way to make a shape like this is to use rounded_prism(), again
>>>> with a difference. However, rounded_prism doesn't make circular roundings,
>>>> so the results will be a bit different, and it will not be possible to
>>>> assure a uniform width at the corners. (Roundovers here are continuous
>>>> curvature beziers. The k parameter controls how gentle the transition,
>>>> with a value of .8 close to circular. Smaller k values will give gentler
>>>> transitions, but then large joint distance may be desired. Try changing k
>>>> to 0.5 to see the difference.)
>>>>
>>>> include<BOSL2/std.scad>
>>>> include<BOSL2/rounding.scad>
>>>>
>>>> $fa=1;$fs=1;
>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>
>>>> diff(){
>>>> rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
>>>>
>>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>>> joint_top=-2, joint_sides=6,k=.8);
>>>> }
>>>>
>>>>
>>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>>> sprabhakar2006@gmail.com> wrote:
>>>>
>>>>> I will explain the process
>>>>> I think this is important.
>>>>>
>>>>> There are 2 approaches.
>>>>> 1. Extrude a section along a path
>>>>> 2. Make a section and offset it multiple times to generate a solid.
>>>>>
>>>>> I am sure this explanation is not enough. Will create a visual
>>>>> description and send it to you.
>>>>>
>>>>> For approach 2:
>>>>> The key is writing a function to offset a section, which I think is
>>>>> not so easy.
>>>>>
>>>>>
>>>>>
>>>>>
>>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com> wrote:
>>>>>
>>>>>> Hi Sanjeev,
>>>>>>
>>>>>>
>>>>>> Thank you. It's beautiful, but how did you generate all those points??
>>>>>>
>>>>>>
>>>>>> I had to hollow out the part a bit and change the shape some so I
>>>>>> would like to find a more generic way to round the edges.
>>>>>>
>>>>>>
>>>>>>
>>>>>> Bob
>>>>>>
>>>>>>
>>>>>>
>>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>>
>>>>>> attached file
>>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>>
>>>>>>
>>>>>>
>>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com> wrote:
>>>>>>
>>>>>>> Hello OpenSCAD,
>>>>>>>
>>>>>>> I want the bottom to be straight and the top inside and outside
>>>>>>> edges to have 2mm roundover
>>>>>>>
>>>>>>> Thank you.
>>>>>>>
>>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>>
>>>>>>> W=34;
>>>>>>> L=60;
>>>>>>> H=10;
>>>>>>> Or = 8;
>>>>>>> Ir = 3;
>>>>>>>
>>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>>
>>>>>>> --
>>>>>>> Best regards,
>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>>
>>>>>> --
>>>>>> have Fun,
>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>> <roosbob@wybatap.com>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

SP
Sanjeev Prabhakar
Sun, Sep 3, 2023 11:44 PM
attached is the offset function calculation steps.
this works fairly well in most of the cases
On Sun, 3 Sept 2023 at 22:13, Adrian Mariano avm4@cornell.edu wrote:
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step you
write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is quite
elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original section
such that the radius of the round is equal to offset required minus some
very small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I don't know how you implemented offset, either in python or in
OpenSCAD, but the problem I have is that checking for invalid portions of
the path after doing the basic offset becomes a quadratic run time task in
OpenSCAD. In other languages, it is possible to use clever data structures
and I think do it in N log N. I saw an algorithm for offset that involves
doing the basic offset and then keeping only the parts of the result that
meet a criterion based on winding number, but the computation to partition
the path into its regions and compute the winding number is very slow in
OpenSCAD, again because without data structures, everything has at least
quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have observed the offset function I wrote in openscad was much slower
than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the methods
seem to be almost equally efficient or inefficient, whatever way you want
to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu wrote:
I think that Sanjeev has identified the two main approaches. You can
make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded rectangle
which avoids issues with self-intersection of the sweep. This is probably
the best way to do this in terms of efficiency. Note also that using
turtle() to compute a rounded rectangle is overkill. I only use turtle()
for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible
using offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside
directly and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(), again
with a difference. However, rounded_prism doesn't make circular roundings,
so the results will be a bit different, and it will not be possible to
assure a uniform width at the corners. (Roundovers here are continuous
curvature beziers. The k parameter controls how gentle the transition,
with a value of .8 close to circular. Smaller k values will give gentler
transitions, but then large joint distance may be desired. Try changing k
to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is
not so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those
points??
I had to hollow out the part a bit and change the shape some so I
would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside
edges to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
attached is the offset function calculation steps.
this works fairly well in most of the cases
On Sun, 3 Sept 2023 at 22:13, Adrian Mariano <avm4@cornell.edu> wrote:
> Step 2, to calculate the intersection of segments is n log n via the
> Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
> and binary search tree, which is impossible in OpenSCAD.
>
> My implementation doesn't handle global intersections, but the step you
> write in 6 of "check if any point is inside these shapes" is also
> quadratic, at least when done naively.
>
> The algorithm I described vaguely above involving winding numbers is quite
> elegant, but I had three problems: 1. cannot work on a path with
> endpoints, 2. difficult to maintain association between vertices in
> original and offset polygon, and 3. not efficient in OpenSCAD. I
> implemented it and is probably more robust, but it was much slower than my
> existing method.
>
> Here's the paper on that algorithm:
> https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
>
> In python I would think you could find libraries already written with
> efficient algorithms for this stuff.
>
> On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> It is quadratic for sure.
>>
>> It needs a separate discussion as per me as this is a complex topic.
>>
>> If I remember correctly following are the steps
>>
>> 1. Original section is divided in to line segments.
>>
>> 2. Each line segment is offset by the amount required and intersection
>> between 2 adjacent segments are calculated. In case of concave segments
>> there would not be any intersection.
>>
>> 3. There could be global intersection of segments apart from the
>> intersection created in step 2. To calculate this it has to be quadratic.
>>
>> 4. All the points obtained in step 2 and step 3 to be added in simple
>> offset of all the original points.
>>
>> 5. create a rounded shape around each segment of the original section
>> such that the radius of the round is equal to offset required minus some
>> very small value like 0.001.
>>
>> 6. Now check if any point is inside these rounded shapes and discard it.
>>
>> Balance points needs to be ordered based on the original points .
>>
>> Now, this seems to be a complicated process, but I think this is the
>> simplest way to achieve a offset.
>>
>>
>> On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu> wrote:
>>
>>> Sanjeev, I don't know how you implemented offset, either in python or in
>>> OpenSCAD, but the problem I have is that checking for invalid portions of
>>> the path after doing the basic offset becomes a quadratic run time task in
>>> OpenSCAD. In other languages, it is possible to use clever data structures
>>> and I think do it in N log N. I saw an algorithm for offset that involves
>>> doing the basic offset and then keeping only the parts of the result that
>>> meet a criterion based on winding number, but the computation to partition
>>> the path into its regions and compute the winding number is very slow in
>>> OpenSCAD, again because without data structures, everything has at least
>>> quadratic run time.
>>>
>>> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> I have observed the offset function I wrote in openscad was much slower
>>>> than the offset function written in python.
>>>>
>>>> Maybe the numpy has a lot of support and is faster. So both the methods
>>>> seem to be almost equally efficient or inefficient, whatever way you want
>>>> to look at it.
>>>>
>>>> also missed to share that the skeleton of the path extrude method is
>>>> different from the offset method.
>>>>
>>>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>>>
>>>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu> wrote:
>>>>
>>>>> I think that Sanjeev has identified the two main approaches. You can
>>>>> make a rounded rectangle shape and sweep. That would look like this:
>>>>>
>>>>> include<BOSL2/std.scad>
>>>>>
>>>>> $fa=1;$fs=1;
>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>
>>>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>>>> path = rect([W,L],rounding=Ir);
>>>>> path_sweep(section,path,closed=true);
>>>>>
>>>>> Note that I have chosen as the sweep path the inner rounded rectangle
>>>>> which avoids issues with self-intersection of the sweep. This is probably
>>>>> the best way to do this in terms of efficiency. Note also that using
>>>>> turtle() to compute a rounded rectangle is overkill. I only use turtle()
>>>>> for shapes that are somehow irregular.
>>>>>
>>>>> Sanjeev's second approach is to use offsetting. This is possible
>>>>> using offset_sweep(), but will likely be slower than path_sweep() because
>>>>> computing offset in userspace is slow. To do this, you have to compute the
>>>>> outside rounded shape and then subtract the inner rounded shape. So it
>>>>> could be done like this:
>>>>>
>>>>> include<BOSL2/std.scad>
>>>>> include<BOSL2/rounding.scad>
>>>>>
>>>>> $fa=1;$fs=1;
>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>
>>>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>>>> outside = rect([W,L], rounding=Or);
>>>>>
>>>>> difference(){
>>>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>>>> }
>>>>>
>>>>> Note that you could also compute just one of inside and outside
>>>>> directly and get the other one with offset().
>>>>>
>>>>> A third way to make a shape like this is to use rounded_prism(), again
>>>>> with a difference. However, rounded_prism doesn't make circular roundings,
>>>>> so the results will be a bit different, and it will not be possible to
>>>>> assure a uniform width at the corners. (Roundovers here are continuous
>>>>> curvature beziers. The k parameter controls how gentle the transition,
>>>>> with a value of .8 close to circular. Smaller k values will give gentler
>>>>> transitions, but then large joint distance may be desired. Try changing k
>>>>> to 0.5 to see the difference.)
>>>>>
>>>>> include<BOSL2/std.scad>
>>>>> include<BOSL2/rounding.scad>
>>>>>
>>>>> $fa=1;$fs=1;
>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>
>>>>> diff(){
>>>>> rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
>>>>>
>>>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>>>> joint_top=-2, joint_sides=6,k=.8);
>>>>> }
>>>>>
>>>>>
>>>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>
>>>>>> I will explain the process
>>>>>> I think this is important.
>>>>>>
>>>>>> There are 2 approaches.
>>>>>> 1. Extrude a section along a path
>>>>>> 2. Make a section and offset it multiple times to generate a solid.
>>>>>>
>>>>>> I am sure this explanation is not enough. Will create a visual
>>>>>> description and send it to you.
>>>>>>
>>>>>> For approach 2:
>>>>>> The key is writing a function to offset a section, which I think is
>>>>>> not so easy.
>>>>>>
>>>>>>
>>>>>>
>>>>>>
>>>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com> wrote:
>>>>>>
>>>>>>> Hi Sanjeev,
>>>>>>>
>>>>>>>
>>>>>>> Thank you. It's beautiful, but how did you generate all those
>>>>>>> points??
>>>>>>>
>>>>>>>
>>>>>>> I had to hollow out the part a bit and change the shape some so I
>>>>>>> would like to find a more generic way to round the edges.
>>>>>>>
>>>>>>>
>>>>>>>
>>>>>>> Bob
>>>>>>>
>>>>>>>
>>>>>>>
>>>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>>>
>>>>>>> attached file
>>>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>>>
>>>>>>>
>>>>>>>
>>>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com> wrote:
>>>>>>>
>>>>>>>> Hello OpenSCAD,
>>>>>>>>
>>>>>>>> I want the bottom to be straight and the top inside and outside
>>>>>>>> edges to have 2mm roundover
>>>>>>>>
>>>>>>>> Thank you.
>>>>>>>>
>>>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>>>
>>>>>>>> W=34;
>>>>>>>> L=60;
>>>>>>>> H=10;
>>>>>>>> Or = 8;
>>>>>>>> Ir = 3;
>>>>>>>>
>>>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>>>
>>>>>>>> --
>>>>>>>> Best regards,
>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>>
>>>>>>> --
>>>>>>> have Fun,
>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>> <roosbob@wybatap.com>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
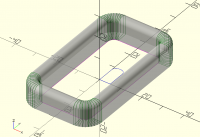

AM
Adrian Mariano
Mon, Sep 4, 2023 10:11 PM
Sanjeev, I examined your algorithm and it seems reasonable. I think it is
more robust than my approach, but maybe somewhat slower. (I try to
identify segments that have a valid portion, discard the rest and compute
intersections just of segments adjacent to discarded ones. But the
heuristic for finding valid segments can fail, and I don't handle global
intersections.) There seems to be a lot of literature about this
problem. I was wondering about reference 15 from the paper I listed, Choi,
B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
of the paper. Very often these results sound interesting but require
special data structures and won't be efficient in OpenSCAD. Note that the
paper I posted based on the winding number claims that the run time of
their entire offset process is O((n+k)log n) for input with length n and
offset curve containing k intersections. I think this run time may be
achievable in Python, but is impossible in OpenSCAD.
On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
attached is the offset function calculation steps.
this works fairly well in most of the cases
On Sun, 3 Sept 2023 at 22:13, Adrian Mariano avm4@cornell.edu wrote:
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step you
write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is
quite elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original section
such that the radius of the round is equal to offset required minus some
very small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I don't know how you implemented offset, either in python or
in OpenSCAD, but the problem I have is that checking for invalid portions
of the path after doing the basic offset becomes a quadratic run time task
in OpenSCAD. In other languages, it is possible to use clever data
structures and I think do it in N log N. I saw an algorithm for offset
that involves doing the basic offset and then keeping only the parts of the
result that meet a criterion based on winding number, but the computation
to partition the path into its regions and compute the winding number is
very slow in OpenSCAD, again because without data structures, everything
has at least quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have observed the offset function I wrote in openscad was much
slower than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the
methods seem to be almost equally efficient or inefficient, whatever way
you want to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu wrote:
I think that Sanjeev has identified the two main approaches. You can
make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded rectangle
which avoids issues with self-intersection of the sweep. This is probably
the best way to do this in terms of efficiency. Note also that using
turtle() to compute a rounded rectangle is overkill. I only use turtle()
for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible
using offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside
directly and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(),
again with a difference. However, rounded_prism doesn't make circular
roundings, so the results will be a bit different, and it will not be
possible to assure a uniform width at the corners. (Roundovers here are
continuous curvature beziers. The k parameter controls how gentle the
transition, with a value of .8 close to circular. Smaller k values will
give gentler transitions, but then large joint distance may be desired.
Try changing k to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is
not so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those
points??
I had to hollow out the part a bit and change the shape some so I
would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside
edges to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Sanjeev, I examined your algorithm and it seems reasonable. I think it is
more robust than my approach, but maybe somewhat slower. (I try to
identify segments that have a valid portion, discard the rest and compute
intersections just of segments adjacent to discarded ones. But the
heuristic for finding valid segments can fail, and I don't handle global
intersections.) There seems to be a lot of literature about this
problem. I was wondering about reference 15 from the paper I listed, Choi,
B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
of the paper. Very often these results sound interesting but require
special data structures and won't be efficient in OpenSCAD. Note that the
paper I posted based on the winding number claims that the run time of
their entire offset process is O((n+k)log n) for input with length n and
offset curve containing k intersections. I think this run time may be
achievable in Python, but is impossible in OpenSCAD.
On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> attached is the offset function calculation steps.
> this works fairly well in most of the cases
>
>
> On Sun, 3 Sept 2023 at 22:13, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Step 2, to calculate the intersection of segments is n log n via the
>> Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
>> and binary search tree, which is impossible in OpenSCAD.
>>
>> My implementation doesn't handle global intersections, but the step you
>> write in 6 of "check if any point is inside these shapes" is also
>> quadratic, at least when done naively.
>>
>> The algorithm I described vaguely above involving winding numbers is
>> quite elegant, but I had three problems: 1. cannot work on a path with
>> endpoints, 2. difficult to maintain association between vertices in
>> original and offset polygon, and 3. not efficient in OpenSCAD. I
>> implemented it and is probably more robust, but it was much slower than my
>> existing method.
>>
>> Here's the paper on that algorithm:
>> https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
>>
>> In python I would think you could find libraries already written with
>> efficient algorithms for this stuff.
>>
>> On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> It is quadratic for sure.
>>>
>>> It needs a separate discussion as per me as this is a complex topic.
>>>
>>> If I remember correctly following are the steps
>>>
>>> 1. Original section is divided in to line segments.
>>>
>>> 2. Each line segment is offset by the amount required and intersection
>>> between 2 adjacent segments are calculated. In case of concave segments
>>> there would not be any intersection.
>>>
>>> 3. There could be global intersection of segments apart from the
>>> intersection created in step 2. To calculate this it has to be quadratic.
>>>
>>> 4. All the points obtained in step 2 and step 3 to be added in simple
>>> offset of all the original points.
>>>
>>> 5. create a rounded shape around each segment of the original section
>>> such that the radius of the round is equal to offset required minus some
>>> very small value like 0.001.
>>>
>>> 6. Now check if any point is inside these rounded shapes and discard it.
>>>
>>> Balance points needs to be ordered based on the original points .
>>>
>>> Now, this seems to be a complicated process, but I think this is the
>>> simplest way to achieve a offset.
>>>
>>>
>>> On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu> wrote:
>>>
>>>> Sanjeev, I don't know how you implemented offset, either in python or
>>>> in OpenSCAD, but the problem I have is that checking for invalid portions
>>>> of the path after doing the basic offset becomes a quadratic run time task
>>>> in OpenSCAD. In other languages, it is possible to use clever data
>>>> structures and I think do it in N log N. I saw an algorithm for offset
>>>> that involves doing the basic offset and then keeping only the parts of the
>>>> result that meet a criterion based on winding number, but the computation
>>>> to partition the path into its regions and compute the winding number is
>>>> very slow in OpenSCAD, again because without data structures, everything
>>>> has at least quadratic run time.
>>>>
>>>> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
>>>> sprabhakar2006@gmail.com> wrote:
>>>>
>>>>> I have observed the offset function I wrote in openscad was much
>>>>> slower than the offset function written in python.
>>>>>
>>>>> Maybe the numpy has a lot of support and is faster. So both the
>>>>> methods seem to be almost equally efficient or inefficient, whatever way
>>>>> you want to look at it.
>>>>>
>>>>> also missed to share that the skeleton of the path extrude method is
>>>>> different from the offset method.
>>>>>
>>>>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>>>>
>>>>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu> wrote:
>>>>>
>>>>>> I think that Sanjeev has identified the two main approaches. You can
>>>>>> make a rounded rectangle shape and sweep. That would look like this:
>>>>>>
>>>>>> include<BOSL2/std.scad>
>>>>>>
>>>>>> $fa=1;$fs=1;
>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>
>>>>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>>>>> path = rect([W,L],rounding=Ir);
>>>>>> path_sweep(section,path,closed=true);
>>>>>>
>>>>>> Note that I have chosen as the sweep path the inner rounded rectangle
>>>>>> which avoids issues with self-intersection of the sweep. This is probably
>>>>>> the best way to do this in terms of efficiency. Note also that using
>>>>>> turtle() to compute a rounded rectangle is overkill. I only use turtle()
>>>>>> for shapes that are somehow irregular.
>>>>>>
>>>>>> Sanjeev's second approach is to use offsetting. This is possible
>>>>>> using offset_sweep(), but will likely be slower than path_sweep() because
>>>>>> computing offset in userspace is slow. To do this, you have to compute the
>>>>>> outside rounded shape and then subtract the inner rounded shape. So it
>>>>>> could be done like this:
>>>>>>
>>>>>> include<BOSL2/std.scad>
>>>>>> include<BOSL2/rounding.scad>
>>>>>>
>>>>>> $fa=1;$fs=1;
>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>
>>>>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>>>>> outside = rect([W,L], rounding=Or);
>>>>>>
>>>>>> difference(){
>>>>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>>>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>>>>> }
>>>>>>
>>>>>> Note that you could also compute just one of inside and outside
>>>>>> directly and get the other one with offset().
>>>>>>
>>>>>> A third way to make a shape like this is to use rounded_prism(),
>>>>>> again with a difference. However, rounded_prism doesn't make circular
>>>>>> roundings, so the results will be a bit different, and it will not be
>>>>>> possible to assure a uniform width at the corners. (Roundovers here are
>>>>>> continuous curvature beziers. The k parameter controls how gentle the
>>>>>> transition, with a value of .8 close to circular. Smaller k values will
>>>>>> give gentler transitions, but then large joint distance may be desired.
>>>>>> Try changing k to 0.5 to see the difference.)
>>>>>>
>>>>>> include<BOSL2/std.scad>
>>>>>> include<BOSL2/rounding.scad>
>>>>>>
>>>>>> $fa=1;$fs=1;
>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>
>>>>>> diff(){
>>>>>> rounded_prism(rect([W,L]),height=H, joint_top=2, joint_sides=8,k=.8)
>>>>>>
>>>>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>>>>> joint_top=-2, joint_sides=6,k=.8);
>>>>>> }
>>>>>>
>>>>>>
>>>>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>
>>>>>>> I will explain the process
>>>>>>> I think this is important.
>>>>>>>
>>>>>>> There are 2 approaches.
>>>>>>> 1. Extrude a section along a path
>>>>>>> 2. Make a section and offset it multiple times to generate a solid.
>>>>>>>
>>>>>>> I am sure this explanation is not enough. Will create a visual
>>>>>>> description and send it to you.
>>>>>>>
>>>>>>> For approach 2:
>>>>>>> The key is writing a function to offset a section, which I think is
>>>>>>> not so easy.
>>>>>>>
>>>>>>>
>>>>>>>
>>>>>>>
>>>>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com> wrote:
>>>>>>>
>>>>>>>> Hi Sanjeev,
>>>>>>>>
>>>>>>>>
>>>>>>>> Thank you. It's beautiful, but how did you generate all those
>>>>>>>> points??
>>>>>>>>
>>>>>>>>
>>>>>>>> I had to hollow out the part a bit and change the shape some so I
>>>>>>>> would like to find a more generic way to round the edges.
>>>>>>>>
>>>>>>>>
>>>>>>>>
>>>>>>>> Bob
>>>>>>>>
>>>>>>>>
>>>>>>>>
>>>>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>>>>
>>>>>>>> attached file
>>>>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>>>>
>>>>>>>>
>>>>>>>>
>>>>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com> wrote:
>>>>>>>>
>>>>>>>>> Hello OpenSCAD,
>>>>>>>>>
>>>>>>>>> I want the bottom to be straight and the top inside and outside
>>>>>>>>> edges to have 2mm roundover
>>>>>>>>>
>>>>>>>>> Thank you.
>>>>>>>>>
>>>>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>>>>
>>>>>>>>> W=34;
>>>>>>>>> L=60;
>>>>>>>>> H=10;
>>>>>>>>> Or = 8;
>>>>>>>>> Ir = 3;
>>>>>>>>>
>>>>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>>>>
>>>>>>>>> --
>>>>>>>>> Best regards,
>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>> _______________________________________________
>>>>>>>>> OpenSCAD mailing list
>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>
>>>>>>>>
>>>>>>>> --
>>>>>>>> have Fun,
>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>> <roosbob@wybatap.com>
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
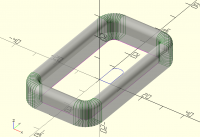

SP
Sanjeev Prabhakar
Tue, Sep 5, 2023 12:01 AM
Hi Adrian,
Read the winding number concept.
what i understood from this is following:
- original loop is ccw (if we don't consider the inner loops for time being)
- after offsetting the edges, find global intersections
- check clockwise loops and discard them and the remaining will be the
offset loop.
Will check this weekend how to implement this.
for pairwise offset: is this edge offset?
In case it is edge offset, the way I do this is by drawing a normal to the
edge.
e.g. let p0 and p1 are the first and the second points of the edge or line
or segment of a loop.
vector = p1-p0 or I would call this p01
any normal drawn to the left of the vector will be inside the loop as I
draw all the sections ccw.
similarly for the right.
On Tue, 5 Sept 2023 at 03:41, Adrian Mariano avm4@cornell.edu wrote:
Sanjeev, I examined your algorithm and it seems reasonable. I think it is
more robust than my approach, but maybe somewhat slower. (I try to
identify segments that have a valid portion, discard the rest and compute
intersections just of segments adjacent to discarded ones. But the
heuristic for finding valid segments can fail, and I don't handle global
intersections.) There seems to be a lot of literature about this
problem. I was wondering about reference 15 from the paper I listed, Choi,
B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
of the paper. Very often these results sound interesting but require
special data structures and won't be efficient in OpenSCAD. Note that the
paper I posted based on the winding number claims that the run time of
their entire offset process is O((n+k)log n) for input with length n and
offset curve containing k intersections. I think this run time may be
achievable in Python, but is impossible in OpenSCAD.
On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
attached is the offset function calculation steps.
this works fairly well in most of the cases
On Sun, 3 Sept 2023 at 22:13, Adrian Mariano avm4@cornell.edu wrote:
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step you
write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is
quite elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original section
such that the radius of the round is equal to offset required minus some
very small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu wrote:
Sanjeev, I don't know how you implemented offset, either in python or
in OpenSCAD, but the problem I have is that checking for invalid portions
of the path after doing the basic offset becomes a quadratic run time task
in OpenSCAD. In other languages, it is possible to use clever data
structures and I think do it in N log N. I saw an algorithm for offset
that involves doing the basic offset and then keeping only the parts of the
result that meet a criterion based on winding number, but the computation
to partition the path into its regions and compute the winding number is
very slow in OpenSCAD, again because without data structures, everything
has at least quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have observed the offset function I wrote in openscad was much
slower than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the
methods seem to be almost equally efficient or inefficient, whatever way
you want to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu
wrote:
I think that Sanjeev has identified the two main approaches. You
can make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded
rectangle which avoids issues with self-intersection of the sweep. This is
probably the best way to do this in terms of efficiency. Note also that
using turtle() to compute a rounded rectangle is overkill. I only use
turtle() for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible
using offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside
directly and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(),
again with a difference. However, rounded_prism doesn't make circular
roundings, so the results will be a bit different, and it will not be
possible to assure a uniform width at the corners. (Roundovers here are
continuous curvature beziers. The k parameter controls how gentle the
transition, with a value of .8 close to circular. Smaller k values will
give gentler transitions, but then large joint distance may be desired.
Try changing k to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2,
joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think is
not so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com
wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those
points??
I had to hollow out the part a bit and change the shape some so I
would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com
wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside
edges to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Hi Adrian,
Read the winding number concept.
what i understood from this is following:
- original loop is ccw (if we don't consider the inner loops for time being)
- after offsetting the edges, find global intersections
- check clockwise loops and discard them and the remaining will be the
offset loop.
Will check this weekend how to implement this.
for pairwise offset: is this edge offset?
In case it is edge offset, the way I do this is by drawing a normal to the
edge.
e.g. let p0 and p1 are the first and the second points of the edge or line
or segment of a loop.
vector = p1-p0 or I would call this p01
any normal drawn to the left of the vector will be inside the loop as I
draw all the sections ccw.
similarly for the right.
On Tue, 5 Sept 2023 at 03:41, Adrian Mariano <avm4@cornell.edu> wrote:
> Sanjeev, I examined your algorithm and it seems reasonable. I think it is
> more robust than my approach, but maybe somewhat slower. (I try to
> identify segments that have a valid portion, discard the rest and compute
> intersections just of segments adjacent to discarded ones. But the
> heuristic for finding valid segments can fail, and I don't handle global
> intersections.) There seems to be a lot of literature about this
> problem. I was wondering about reference 15 from the paper I listed, Choi,
> B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
> curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
> of the paper. Very often these results sound interesting but require
> special data structures and won't be efficient in OpenSCAD. Note that the
> paper I posted based on the winding number claims that the run time of
> their entire offset process is O((n+k)log n) for input with length n and
> offset curve containing k intersections. I think this run time may be
> achievable in Python, but is impossible in OpenSCAD.
>
>
>
> On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> attached is the offset function calculation steps.
>> this works fairly well in most of the cases
>>
>>
>> On Sun, 3 Sept 2023 at 22:13, Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Step 2, to calculate the intersection of segments is n log n via the
>>> Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
>>> and binary search tree, which is impossible in OpenSCAD.
>>>
>>> My implementation doesn't handle global intersections, but the step you
>>> write in 6 of "check if any point is inside these shapes" is also
>>> quadratic, at least when done naively.
>>>
>>> The algorithm I described vaguely above involving winding numbers is
>>> quite elegant, but I had three problems: 1. cannot work on a path with
>>> endpoints, 2. difficult to maintain association between vertices in
>>> original and offset polygon, and 3. not efficient in OpenSCAD. I
>>> implemented it and is probably more robust, but it was much slower than my
>>> existing method.
>>>
>>> Here's the paper on that algorithm:
>>> https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
>>>
>>> In python I would think you could find libraries already written with
>>> efficient algorithms for this stuff.
>>>
>>> On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> It is quadratic for sure.
>>>>
>>>> It needs a separate discussion as per me as this is a complex topic.
>>>>
>>>> If I remember correctly following are the steps
>>>>
>>>> 1. Original section is divided in to line segments.
>>>>
>>>> 2. Each line segment is offset by the amount required and intersection
>>>> between 2 adjacent segments are calculated. In case of concave segments
>>>> there would not be any intersection.
>>>>
>>>> 3. There could be global intersection of segments apart from the
>>>> intersection created in step 2. To calculate this it has to be quadratic.
>>>>
>>>> 4. All the points obtained in step 2 and step 3 to be added in simple
>>>> offset of all the original points.
>>>>
>>>> 5. create a rounded shape around each segment of the original section
>>>> such that the radius of the round is equal to offset required minus some
>>>> very small value like 0.001.
>>>>
>>>> 6. Now check if any point is inside these rounded shapes and discard it.
>>>>
>>>> Balance points needs to be ordered based on the original points .
>>>>
>>>> Now, this seems to be a complicated process, but I think this is the
>>>> simplest way to achieve a offset.
>>>>
>>>>
>>>> On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu> wrote:
>>>>
>>>>> Sanjeev, I don't know how you implemented offset, either in python or
>>>>> in OpenSCAD, but the problem I have is that checking for invalid portions
>>>>> of the path after doing the basic offset becomes a quadratic run time task
>>>>> in OpenSCAD. In other languages, it is possible to use clever data
>>>>> structures and I think do it in N log N. I saw an algorithm for offset
>>>>> that involves doing the basic offset and then keeping only the parts of the
>>>>> result that meet a criterion based on winding number, but the computation
>>>>> to partition the path into its regions and compute the winding number is
>>>>> very slow in OpenSCAD, again because without data structures, everything
>>>>> has at least quadratic run time.
>>>>>
>>>>> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>
>>>>>> I have observed the offset function I wrote in openscad was much
>>>>>> slower than the offset function written in python.
>>>>>>
>>>>>> Maybe the numpy has a lot of support and is faster. So both the
>>>>>> methods seem to be almost equally efficient or inefficient, whatever way
>>>>>> you want to look at it.
>>>>>>
>>>>>> also missed to share that the skeleton of the path extrude method is
>>>>>> different from the offset method.
>>>>>>
>>>>>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>>>>>
>>>>>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu>
>>>>>> wrote:
>>>>>>
>>>>>>> I think that Sanjeev has identified the two main approaches. You
>>>>>>> can make a rounded rectangle shape and sweep. That would look like this:
>>>>>>>
>>>>>>> include<BOSL2/std.scad>
>>>>>>>
>>>>>>> $fa=1;$fs=1;
>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>
>>>>>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>>>>>> path = rect([W,L],rounding=Ir);
>>>>>>> path_sweep(section,path,closed=true);
>>>>>>>
>>>>>>> Note that I have chosen as the sweep path the inner rounded
>>>>>>> rectangle which avoids issues with self-intersection of the sweep. This is
>>>>>>> probably the best way to do this in terms of efficiency. Note also that
>>>>>>> using turtle() to compute a rounded rectangle is overkill. I only use
>>>>>>> turtle() for shapes that are somehow irregular.
>>>>>>>
>>>>>>> Sanjeev's second approach is to use offsetting. This is possible
>>>>>>> using offset_sweep(), but will likely be slower than path_sweep() because
>>>>>>> computing offset in userspace is slow. To do this, you have to compute the
>>>>>>> outside rounded shape and then subtract the inner rounded shape. So it
>>>>>>> could be done like this:
>>>>>>>
>>>>>>> include<BOSL2/std.scad>
>>>>>>> include<BOSL2/rounding.scad>
>>>>>>>
>>>>>>> $fa=1;$fs=1;
>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>
>>>>>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>>>>>> outside = rect([W,L], rounding=Or);
>>>>>>>
>>>>>>> difference(){
>>>>>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>>>>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>>>>>> }
>>>>>>>
>>>>>>> Note that you could also compute just one of inside and outside
>>>>>>> directly and get the other one with offset().
>>>>>>>
>>>>>>> A third way to make a shape like this is to use rounded_prism(),
>>>>>>> again with a difference. However, rounded_prism doesn't make circular
>>>>>>> roundings, so the results will be a bit different, and it will not be
>>>>>>> possible to assure a uniform width at the corners. (Roundovers here are
>>>>>>> continuous curvature beziers. The k parameter controls how gentle the
>>>>>>> transition, with a value of .8 close to circular. Smaller k values will
>>>>>>> give gentler transitions, but then large joint distance may be desired.
>>>>>>> Try changing k to 0.5 to see the difference.)
>>>>>>>
>>>>>>> include<BOSL2/std.scad>
>>>>>>> include<BOSL2/rounding.scad>
>>>>>>>
>>>>>>> $fa=1;$fs=1;
>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>
>>>>>>> diff(){
>>>>>>> rounded_prism(rect([W,L]),height=H, joint_top=2,
>>>>>>> joint_sides=8,k=.8)
>>>>>>>
>>>>>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>>>>>> joint_top=-2, joint_sides=6,k=.8);
>>>>>>> }
>>>>>>>
>>>>>>>
>>>>>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>>
>>>>>>>> I will explain the process
>>>>>>>> I think this is important.
>>>>>>>>
>>>>>>>> There are 2 approaches.
>>>>>>>> 1. Extrude a section along a path
>>>>>>>> 2. Make a section and offset it multiple times to generate a solid.
>>>>>>>>
>>>>>>>> I am sure this explanation is not enough. Will create a visual
>>>>>>>> description and send it to you.
>>>>>>>>
>>>>>>>> For approach 2:
>>>>>>>> The key is writing a function to offset a section, which I think is
>>>>>>>> not so easy.
>>>>>>>>
>>>>>>>>
>>>>>>>>
>>>>>>>>
>>>>>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com>
>>>>>>>> wrote:
>>>>>>>>
>>>>>>>>> Hi Sanjeev,
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> Thank you. It's beautiful, but how did you generate all those
>>>>>>>>> points??
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> I had to hollow out the part a bit and change the shape some so I
>>>>>>>>> would like to find a more generic way to round the edges.
>>>>>>>>>
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> Bob
>>>>>>>>>
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>>>>>
>>>>>>>>> attached file
>>>>>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>>>>>
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com>
>>>>>>>>> wrote:
>>>>>>>>>
>>>>>>>>>> Hello OpenSCAD,
>>>>>>>>>>
>>>>>>>>>> I want the bottom to be straight and the top inside and outside
>>>>>>>>>> edges to have 2mm roundover
>>>>>>>>>>
>>>>>>>>>> Thank you.
>>>>>>>>>>
>>>>>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>>>>>
>>>>>>>>>> W=34;
>>>>>>>>>> L=60;
>>>>>>>>>> H=10;
>>>>>>>>>> Or = 8;
>>>>>>>>>> Ir = 3;
>>>>>>>>>>
>>>>>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>>>>>
>>>>>>>>>> --
>>>>>>>>>> Best regards,
>>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>>> _______________________________________________
>>>>>>>>>> OpenSCAD mailing list
>>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>>
>>>>>>>>>
>>>>>>>>> --
>>>>>>>>> have Fun,
>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>> <roosbob@wybatap.com>
>>>>>>>>> _______________________________________________
>>>>>>>>> OpenSCAD mailing list
>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
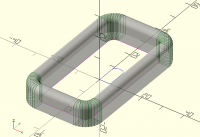

AM
Adrian Mariano
Tue, Sep 5, 2023 2:48 AM
I think your understanding of the paper is basically correct. You have to
draw the raw offset curve in the special way they describe. And of course
you need to decompose the path into its loops after you find the
intersections.
With regards to offsetting an edge, it seems that simply adding normal
edges to produce a polygon will not work because some valid portions of the
offset may be inside, or too close, to the resulting polygon. Also the
edge will incorrectly shrink/grow at the endpoints in the direction tangent
to the starting edge. Maybe I misunderstood something?
On Mon, Sep 4, 2023 at 8:02 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
Hi Adrian,
Read the winding number concept.
what i understood from this is following:
- original loop is ccw (if we don't consider the inner loops for time
being)
- after offsetting the edges, find global intersections
- check clockwise loops and discard them and the remaining will be the
offset loop.
Will check this weekend how to implement this.
for pairwise offset: is this edge offset?
In case it is edge offset, the way I do this is by drawing a normal to the
edge.
e.g. let p0 and p1 are the first and the second points of the edge or line
or segment of a loop.
vector = p1-p0 or I would call this p01
any normal drawn to the left of the vector will be inside the loop as I
draw all the sections ccw.
similarly for the right.
On Tue, 5 Sept 2023 at 03:41, Adrian Mariano avm4@cornell.edu wrote:
Sanjeev, I examined your algorithm and it seems reasonable. I think it
is more robust than my approach, but maybe somewhat slower. (I try to
identify segments that have a valid portion, discard the rest and compute
intersections just of segments adjacent to discarded ones. But the
heuristic for finding valid segments can fail, and I don't handle global
intersections.) There seems to be a lot of literature about this
problem. I was wondering about reference 15 from the paper I listed, Choi,
B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
of the paper. Very often these results sound interesting but require
special data structures and won't be efficient in OpenSCAD. Note that the
paper I posted based on the winding number claims that the run time of
their entire offset process is O((n+k)log n) for input with length n and
offset curve containing k intersections. I think this run time may be
achievable in Python, but is impossible in OpenSCAD.
On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
attached is the offset function calculation steps.
this works fairly well in most of the cases
On Sun, 3 Sept 2023 at 22:13, Adrian Mariano avm4@cornell.edu wrote:
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step you
write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is
quite elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and intersection
between 2 adjacent segments are calculated. In case of concave segments
there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original section
such that the radius of the round is equal to offset required minus some
very small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard
it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu
wrote:
Sanjeev, I don't know how you implemented offset, either in python or
in OpenSCAD, but the problem I have is that checking for invalid portions
of the path after doing the basic offset becomes a quadratic run time task
in OpenSCAD. In other languages, it is possible to use clever data
structures and I think do it in N log N. I saw an algorithm for offset
that involves doing the basic offset and then keeping only the parts of the
result that meet a criterion based on winding number, but the computation
to partition the path into its regions and compute the winding number is
very slow in OpenSCAD, again because without data structures, everything
has at least quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have observed the offset function I wrote in openscad was much
slower than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the
methods seem to be almost equally efficient or inefficient, whatever way
you want to look at it.
also missed to share that the skeleton of the path extrude method is
different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu
wrote:
I think that Sanjeev has identified the two main approaches. You
can make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded
rectangle which avoids issues with self-intersection of the sweep. This is
probably the best way to do this in terms of efficiency. Note also that
using turtle() to compute a rounded rectangle is overkill. I only use
turtle() for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible
using offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside
directly and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(),
again with a difference. However, rounded_prism doesn't make circular
roundings, so the results will be a bit different, and it will not be
possible to assure a uniform width at the corners. (Roundovers here are
continuous curvature beziers. The k parameter controls how gentle the
transition, with a value of .8 close to circular. Smaller k values will
give gentler transitions, but then large joint distance may be desired.
Try changing k to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2,
joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think
is not so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com
wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those
points??
I had to hollow out the part a bit and change the shape some so I
would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com
wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside
edges to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I think your understanding of the paper is basically correct. You have to
draw the raw offset curve in the special way they describe. And of course
you need to decompose the path into its loops after you find the
intersections.
With regards to offsetting an edge, it seems that simply adding normal
edges to produce a polygon will not work because some valid portions of the
offset may be inside, or too close, to the resulting polygon. Also the
edge will incorrectly shrink/grow at the endpoints in the direction tangent
to the starting edge. Maybe I misunderstood something?
On Mon, Sep 4, 2023 at 8:02 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> Hi Adrian,
>
> Read the winding number concept.
> what i understood from this is following:
> - original loop is ccw (if we don't consider the inner loops for time
> being)
> - after offsetting the edges, find global intersections
> - check clockwise loops and discard them and the remaining will be the
> offset loop.
>
> Will check this weekend how to implement this.
>
> for pairwise offset: is this edge offset?
> In case it is edge offset, the way I do this is by drawing a normal to the
> edge.
> e.g. let p0 and p1 are the first and the second points of the edge or line
> or segment of a loop.
> vector = p1-p0 or I would call this p01
> any normal drawn to the left of the vector will be inside the loop as I
> draw all the sections ccw.
> similarly for the right.
>
>
>
>
>
> On Tue, 5 Sept 2023 at 03:41, Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Sanjeev, I examined your algorithm and it seems reasonable. I think it
>> is more robust than my approach, but maybe somewhat slower. (I try to
>> identify segments that have a valid portion, discard the rest and compute
>> intersections just of segments adjacent to discarded ones. But the
>> heuristic for finding valid segments can fail, and I don't handle global
>> intersections.) There seems to be a lot of literature about this
>> problem. I was wondering about reference 15 from the paper I listed, Choi,
>> B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
>> curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
>> of the paper. Very often these results sound interesting but require
>> special data structures and won't be efficient in OpenSCAD. Note that the
>> paper I posted based on the winding number claims that the run time of
>> their entire offset process is O((n+k)log n) for input with length n and
>> offset curve containing k intersections. I think this run time may be
>> achievable in Python, but is impossible in OpenSCAD.
>>
>>
>>
>> On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar <
>> sprabhakar2006@gmail.com> wrote:
>>
>>> attached is the offset function calculation steps.
>>> this works fairly well in most of the cases
>>>
>>>
>>> On Sun, 3 Sept 2023 at 22:13, Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> Step 2, to calculate the intersection of segments is n log n via the
>>>> Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
>>>> and binary search tree, which is impossible in OpenSCAD.
>>>>
>>>> My implementation doesn't handle global intersections, but the step you
>>>> write in 6 of "check if any point is inside these shapes" is also
>>>> quadratic, at least when done naively.
>>>>
>>>> The algorithm I described vaguely above involving winding numbers is
>>>> quite elegant, but I had three problems: 1. cannot work on a path with
>>>> endpoints, 2. difficult to maintain association between vertices in
>>>> original and offset polygon, and 3. not efficient in OpenSCAD. I
>>>> implemented it and is probably more robust, but it was much slower than my
>>>> existing method.
>>>>
>>>> Here's the paper on that algorithm:
>>>> https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
>>>>
>>>> In python I would think you could find libraries already written with
>>>> efficient algorithms for this stuff.
>>>>
>>>> On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
>>>> sprabhakar2006@gmail.com> wrote:
>>>>
>>>>> It is quadratic for sure.
>>>>>
>>>>> It needs a separate discussion as per me as this is a complex topic.
>>>>>
>>>>> If I remember correctly following are the steps
>>>>>
>>>>> 1. Original section is divided in to line segments.
>>>>>
>>>>> 2. Each line segment is offset by the amount required and intersection
>>>>> between 2 adjacent segments are calculated. In case of concave segments
>>>>> there would not be any intersection.
>>>>>
>>>>> 3. There could be global intersection of segments apart from the
>>>>> intersection created in step 2. To calculate this it has to be quadratic.
>>>>>
>>>>> 4. All the points obtained in step 2 and step 3 to be added in simple
>>>>> offset of all the original points.
>>>>>
>>>>> 5. create a rounded shape around each segment of the original section
>>>>> such that the radius of the round is equal to offset required minus some
>>>>> very small value like 0.001.
>>>>>
>>>>> 6. Now check if any point is inside these rounded shapes and discard
>>>>> it.
>>>>>
>>>>> Balance points needs to be ordered based on the original points .
>>>>>
>>>>> Now, this seems to be a complicated process, but I think this is the
>>>>> simplest way to achieve a offset.
>>>>>
>>>>>
>>>>> On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu>
>>>>> wrote:
>>>>>
>>>>>> Sanjeev, I don't know how you implemented offset, either in python or
>>>>>> in OpenSCAD, but the problem I have is that checking for invalid portions
>>>>>> of the path after doing the basic offset becomes a quadratic run time task
>>>>>> in OpenSCAD. In other languages, it is possible to use clever data
>>>>>> structures and I think do it in N log N. I saw an algorithm for offset
>>>>>> that involves doing the basic offset and then keeping only the parts of the
>>>>>> result that meet a criterion based on winding number, but the computation
>>>>>> to partition the path into its regions and compute the winding number is
>>>>>> very slow in OpenSCAD, again because without data structures, everything
>>>>>> has at least quadratic run time.
>>>>>>
>>>>>> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>
>>>>>>> I have observed the offset function I wrote in openscad was much
>>>>>>> slower than the offset function written in python.
>>>>>>>
>>>>>>> Maybe the numpy has a lot of support and is faster. So both the
>>>>>>> methods seem to be almost equally efficient or inefficient, whatever way
>>>>>>> you want to look at it.
>>>>>>>
>>>>>>> also missed to share that the skeleton of the path extrude method is
>>>>>>> different from the offset method.
>>>>>>>
>>>>>>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>>>>>>
>>>>>>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu>
>>>>>>> wrote:
>>>>>>>
>>>>>>>> I think that Sanjeev has identified the two main approaches. You
>>>>>>>> can make a rounded rectangle shape and sweep. That would look like this:
>>>>>>>>
>>>>>>>> include<BOSL2/std.scad>
>>>>>>>>
>>>>>>>> $fa=1;$fs=1;
>>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>>
>>>>>>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>>>>>>> path = rect([W,L],rounding=Ir);
>>>>>>>> path_sweep(section,path,closed=true);
>>>>>>>>
>>>>>>>> Note that I have chosen as the sweep path the inner rounded
>>>>>>>> rectangle which avoids issues with self-intersection of the sweep. This is
>>>>>>>> probably the best way to do this in terms of efficiency. Note also that
>>>>>>>> using turtle() to compute a rounded rectangle is overkill. I only use
>>>>>>>> turtle() for shapes that are somehow irregular.
>>>>>>>>
>>>>>>>> Sanjeev's second approach is to use offsetting. This is possible
>>>>>>>> using offset_sweep(), but will likely be slower than path_sweep() because
>>>>>>>> computing offset in userspace is slow. To do this, you have to compute the
>>>>>>>> outside rounded shape and then subtract the inner rounded shape. So it
>>>>>>>> could be done like this:
>>>>>>>>
>>>>>>>> include<BOSL2/std.scad>
>>>>>>>> include<BOSL2/rounding.scad>
>>>>>>>>
>>>>>>>> $fa=1;$fs=1;
>>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>>
>>>>>>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>>>>>>> outside = rect([W,L], rounding=Or);
>>>>>>>>
>>>>>>>> difference(){
>>>>>>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>>>>>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>>>>>>> }
>>>>>>>>
>>>>>>>> Note that you could also compute just one of inside and outside
>>>>>>>> directly and get the other one with offset().
>>>>>>>>
>>>>>>>> A third way to make a shape like this is to use rounded_prism(),
>>>>>>>> again with a difference. However, rounded_prism doesn't make circular
>>>>>>>> roundings, so the results will be a bit different, and it will not be
>>>>>>>> possible to assure a uniform width at the corners. (Roundovers here are
>>>>>>>> continuous curvature beziers. The k parameter controls how gentle the
>>>>>>>> transition, with a value of .8 close to circular. Smaller k values will
>>>>>>>> give gentler transitions, but then large joint distance may be desired.
>>>>>>>> Try changing k to 0.5 to see the difference.)
>>>>>>>>
>>>>>>>> include<BOSL2/std.scad>
>>>>>>>> include<BOSL2/rounding.scad>
>>>>>>>>
>>>>>>>> $fa=1;$fs=1;
>>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>>
>>>>>>>> diff(){
>>>>>>>> rounded_prism(rect([W,L]),height=H, joint_top=2,
>>>>>>>> joint_sides=8,k=.8)
>>>>>>>>
>>>>>>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>>>>>>> joint_top=-2, joint_sides=6,k=.8);
>>>>>>>> }
>>>>>>>>
>>>>>>>>
>>>>>>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>>>
>>>>>>>>> I will explain the process
>>>>>>>>> I think this is important.
>>>>>>>>>
>>>>>>>>> There are 2 approaches.
>>>>>>>>> 1. Extrude a section along a path
>>>>>>>>> 2. Make a section and offset it multiple times to generate a solid.
>>>>>>>>>
>>>>>>>>> I am sure this explanation is not enough. Will create a visual
>>>>>>>>> description and send it to you.
>>>>>>>>>
>>>>>>>>> For approach 2:
>>>>>>>>> The key is writing a function to offset a section, which I think
>>>>>>>>> is not so easy.
>>>>>>>>>
>>>>>>>>>
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com>
>>>>>>>>> wrote:
>>>>>>>>>
>>>>>>>>>> Hi Sanjeev,
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> Thank you. It's beautiful, but how did you generate all those
>>>>>>>>>> points??
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> I had to hollow out the part a bit and change the shape some so I
>>>>>>>>>> would like to find a more generic way to round the edges.
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> Bob
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>>>>>>
>>>>>>>>>> attached file
>>>>>>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com>
>>>>>>>>>> wrote:
>>>>>>>>>>
>>>>>>>>>>> Hello OpenSCAD,
>>>>>>>>>>>
>>>>>>>>>>> I want the bottom to be straight and the top inside and outside
>>>>>>>>>>> edges to have 2mm roundover
>>>>>>>>>>>
>>>>>>>>>>> Thank you.
>>>>>>>>>>>
>>>>>>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>>>>>>
>>>>>>>>>>> W=34;
>>>>>>>>>>> L=60;
>>>>>>>>>>> H=10;
>>>>>>>>>>> Or = 8;
>>>>>>>>>>> Ir = 3;
>>>>>>>>>>>
>>>>>>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>>>>>>
>>>>>>>>>>> --
>>>>>>>>>>> Best regards,
>>>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>>>> _______________________________________________
>>>>>>>>>>> OpenSCAD mailing list
>>>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> --
>>>>>>>>>> have Fun,
>>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>>> <roosbob@wybatap.com>
>>>>>>>>>> _______________________________________________
>>>>>>>>>> OpenSCAD mailing list
>>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>>
>>>>>>>>> _______________________________________________
>>>>>>>>> OpenSCAD mailing list
>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
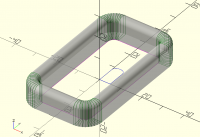

SP
Sanjeev Prabhakar
Tue, Sep 5, 2023 3:59 AM
Actually I am not clear what pair wise offset means . Need to read the
paper you referred to
On Tue, 5 Sept, 2023, 8:19 am Adrian Mariano, avm4@cornell.edu wrote:
I think your understanding of the paper is basically correct. You have to
draw the raw offset curve in the special way they describe. And of course
you need to decompose the path into its loops after you find the
intersections.
With regards to offsetting an edge, it seems that simply adding normal
edges to produce a polygon will not work because some valid portions of the
offset may be inside, or too close, to the resulting polygon. Also the
edge will incorrectly shrink/grow at the endpoints in the direction tangent
to the starting edge. Maybe I misunderstood something?
On Mon, Sep 4, 2023 at 8:02 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
Hi Adrian,
Read the winding number concept.
what i understood from this is following:
- original loop is ccw (if we don't consider the inner loops for time
being)
- after offsetting the edges, find global intersections
- check clockwise loops and discard them and the remaining will be the
offset loop.
Will check this weekend how to implement this.
for pairwise offset: is this edge offset?
In case it is edge offset, the way I do this is by drawing a normal to
the edge.
e.g. let p0 and p1 are the first and the second points of the edge or
line or segment of a loop.
vector = p1-p0 or I would call this p01
any normal drawn to the left of the vector will be inside the loop as I
draw all the sections ccw.
similarly for the right.
On Tue, 5 Sept 2023 at 03:41, Adrian Mariano avm4@cornell.edu wrote:
Sanjeev, I examined your algorithm and it seems reasonable. I think it
is more robust than my approach, but maybe somewhat slower. (I try to
identify segments that have a valid portion, discard the rest and compute
intersections just of segments adjacent to discarded ones. But the
heuristic for finding valid segments can fail, and I don't handle global
intersections.) There seems to be a lot of literature about this
problem. I was wondering about reference 15 from the paper I listed, Choi,
B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
of the paper. Very often these results sound interesting but require
special data structures and won't be efficient in OpenSCAD. Note that the
paper I posted based on the winding number claims that the run time of
their entire offset process is O((n+k)log n) for input with length n and
offset curve containing k intersections. I think this run time may be
achievable in Python, but is impossible in OpenSCAD.
On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
attached is the offset function calculation steps.
this works fairly well in most of the cases
On Sun, 3 Sept 2023 at 22:13, Adrian Mariano avm4@cornell.edu wrote:
Step 2, to calculate the intersection of segments is n log n via the
Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
and binary search tree, which is impossible in OpenSCAD.
My implementation doesn't handle global intersections, but the step
you write in 6 of "check if any point is inside these shapes" is also
quadratic, at least when done naively.
The algorithm I described vaguely above involving winding numbers is
quite elegant, but I had three problems: 1. cannot work on a path with
endpoints, 2. difficult to maintain association between vertices in
original and offset polygon, and 3. not efficient in OpenSCAD. I
implemented it and is probably more robust, but it was much slower than my
existing method.
Here's the paper on that algorithm:
https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
In python I would think you could find libraries already written with
efficient algorithms for this stuff.
On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
It is quadratic for sure.
It needs a separate discussion as per me as this is a complex topic.
If I remember correctly following are the steps
-
Original section is divided in to line segments.
-
Each line segment is offset by the amount required and
intersection between 2 adjacent segments are calculated. In case of concave
segments there would not be any intersection.
-
There could be global intersection of segments apart from the
intersection created in step 2. To calculate this it has to be quadratic.
-
All the points obtained in step 2 and step 3 to be added in simple
offset of all the original points.
-
create a rounded shape around each segment of the original
section such that the radius of the round is equal to offset required minus
some very small value like 0.001.
-
Now check if any point is inside these rounded shapes and discard
it.
Balance points needs to be ordered based on the original points .
Now, this seems to be a complicated process, but I think this is the
simplest way to achieve a offset.
On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, avm4@cornell.edu
wrote:
Sanjeev, I don't know how you implemented offset, either in python
or in OpenSCAD, but the problem I have is that checking for invalid
portions of the path after doing the basic offset becomes a quadratic run
time task in OpenSCAD. In other languages, it is possible to use clever
data structures and I think do it in N log N. I saw an algorithm for
offset that involves doing the basic offset and then keeping only the parts
of the result that meet a criterion based on winding number, but the
computation to partition the path into its regions and compute the winding
number is very slow in OpenSCAD, again because without data structures,
everything has at least quadratic run time.
On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I have observed the offset function I wrote in openscad was much
slower than the offset function written in python.
Maybe the numpy has a lot of support and is faster. So both the
methods seem to be almost equally efficient or inefficient, whatever way
you want to look at it.
also missed to share that the skeleton of the path extrude method
is different from the offset method.
[image: Screenshot 2023-09-03 at 6.55.06 PM.png]
On Sun, 3 Sept 2023 at 18:29, Adrian Mariano avm4@cornell.edu
wrote:
I think that Sanjeev has identified the two main approaches. You
can make a rounded rectangle shape and sweep. That would look like this:
include<BOSL2/std.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
path = rect([W,L],rounding=Ir);
path_sweep(section,path,closed=true);
Note that I have chosen as the sweep path the inner rounded
rectangle which avoids issues with self-intersection of the sweep. This is
probably the best way to do this in terms of efficiency. Note also that
using turtle() to compute a rounded rectangle is overkill. I only use
turtle() for shapes that are somehow irregular.
Sanjeev's second approach is to use offsetting. This is possible
using offset_sweep(), but will likely be slower than path_sweep() because
computing offset in userspace is slow. To do this, you have to compute the
outside rounded shape and then subtract the inner rounded shape. So it
could be done like this:
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
outside = rect([W,L], rounding=Or);
difference(){
offset_sweep(outside, h=H, top=os_circle(r=2));
down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
}
Note that you could also compute just one of inside and outside
directly and get the other one with offset().
A third way to make a shape like this is to use rounded_prism(),
again with a difference. However, rounded_prism doesn't make circular
roundings, so the results will be a bit different, and it will not be
possible to assure a uniform width at the corners. (Roundovers here are
continuous curvature beziers. The k parameter controls how gentle the
transition, with a value of .8 close to circular. Smaller k values will
give gentler transitions, but then large joint distance may be desired.
Try changing k to 0.5 to see the difference.)
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fa=1;$fs=1;
W=34;L=60;H=10;Or = 8;Ir = 3;
diff(){
rounded_prism(rect([W,L]),height=H, joint_top=2,
joint_sides=8,k=.8)
up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
joint_top=-2, joint_sides=6,k=.8);
}
On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
I will explain the process
I think this is important.
There are 2 approaches.
- Extrude a section along a path
- Make a section and offset it multiple times to generate a
solid.
I am sure this explanation is not enough. Will create a visual
description and send it to you.
For approach 2:
The key is writing a function to offset a section, which I think
is not so easy.
On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, roosbob@wybatap.com
wrote:
Hi Sanjeev,
Thank you. It's beautiful, but how did you generate all those
points??
I had to hollow out the part a bit and change the shape some so
I would like to find a more generic way to round the edges.
Bob
Sunday, September 3, 2023, 6:17:54 AM, you wrote:
attached file
[image: Screenshot 2023-09-03 at 3.45.43 PM.png]
On Sun, 3 Sept 2023 at 06:50, Bob Roos roosbob@wybatap.com
wrote:
Hello OpenSCAD,
I want the bottom to be straight and the top inside and outside
edges to have 2mm roundover
Thank you.
include <BOSL2/std.scad> //or screws or threading
W=34;
L=60;
H=10;
Or = 8;
Ir = 3;
rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
--
Best regards,
Bob mailto:roosbob@wybatap.com
OpenSCAD mailing list
To unsubscribe send an email to
discuss-leave@lists.openscad.org
Actually I am not clear what pair wise offset means . Need to read the
paper you referred to
On Tue, 5 Sept, 2023, 8:19 am Adrian Mariano, <avm4@cornell.edu> wrote:
> I think your understanding of the paper is basically correct. You have to
> draw the raw offset curve in the special way they describe. And of course
> you need to decompose the path into its loops after you find the
> intersections.
>
> With regards to offsetting an edge, it seems that simply adding normal
> edges to produce a polygon will not work because some valid portions of the
> offset may be inside, or too close, to the resulting polygon. Also the
> edge will incorrectly shrink/grow at the endpoints in the direction tangent
> to the starting edge. Maybe I misunderstood something?
>
> On Mon, Sep 4, 2023 at 8:02 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> Hi Adrian,
>>
>> Read the winding number concept.
>> what i understood from this is following:
>> - original loop is ccw (if we don't consider the inner loops for time
>> being)
>> - after offsetting the edges, find global intersections
>> - check clockwise loops and discard them and the remaining will be the
>> offset loop.
>>
>> Will check this weekend how to implement this.
>>
>> for pairwise offset: is this edge offset?
>> In case it is edge offset, the way I do this is by drawing a normal to
>> the edge.
>> e.g. let p0 and p1 are the first and the second points of the edge or
>> line or segment of a loop.
>> vector = p1-p0 or I would call this p01
>> any normal drawn to the left of the vector will be inside the loop as I
>> draw all the sections ccw.
>> similarly for the right.
>>
>>
>>
>>
>>
>> On Tue, 5 Sept 2023 at 03:41, Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Sanjeev, I examined your algorithm and it seems reasonable. I think it
>>> is more robust than my approach, but maybe somewhat slower. (I try to
>>> identify segments that have a valid portion, discard the rest and compute
>>> intersections just of segments adjacent to discarded ones. But the
>>> heuristic for finding valid segments can fail, and I don't handle global
>>> intersections.) There seems to be a lot of literature about this
>>> problem. I was wondering about reference 15 from the paper I listed, Choi,
>>> B., and Park, S., 1999. “A pair-wise offset algorithm for 2D point-sequence
>>> curve”. Computer-Aided Design, 31(12), pp. 735–745, but I can't find a copy
>>> of the paper. Very often these results sound interesting but require
>>> special data structures and won't be efficient in OpenSCAD. Note that the
>>> paper I posted based on the winding number claims that the run time of
>>> their entire offset process is O((n+k)log n) for input with length n and
>>> offset curve containing k intersections. I think this run time may be
>>> achievable in Python, but is impossible in OpenSCAD.
>>>
>>>
>>>
>>> On Sun, Sep 3, 2023 at 7:46 PM Sanjeev Prabhakar <
>>> sprabhakar2006@gmail.com> wrote:
>>>
>>>> attached is the offset function calculation steps.
>>>> this works fairly well in most of the cases
>>>>
>>>>
>>>> On Sun, 3 Sept 2023 at 22:13, Adrian Mariano <avm4@cornell.edu> wrote:
>>>>
>>>>> Step 2, to calculate the intersection of segments is n log n via the
>>>>> Bentley-Ottmann (line sweep) algorithm, but it requires a priority queue
>>>>> and binary search tree, which is impossible in OpenSCAD.
>>>>>
>>>>> My implementation doesn't handle global intersections, but the step
>>>>> you write in 6 of "check if any point is inside these shapes" is also
>>>>> quadratic, at least when done naively.
>>>>>
>>>>> The algorithm I described vaguely above involving winding numbers is
>>>>> quite elegant, but I had three problems: 1. cannot work on a path with
>>>>> endpoints, 2. difficult to maintain association between vertices in
>>>>> original and offset polygon, and 3. not efficient in OpenSCAD. I
>>>>> implemented it and is probably more robust, but it was much slower than my
>>>>> existing method.
>>>>>
>>>>> Here's the paper on that algorithm:
>>>>> https://mcmains.me.berkeley.edu/pubs/DAC05OffsetPolygon.pdf
>>>>>
>>>>> In python I would think you could find libraries already written with
>>>>> efficient algorithms for this stuff.
>>>>>
>>>>> On Sun, Sep 3, 2023 at 10:14 AM Sanjeev Prabhakar <
>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>
>>>>>> It is quadratic for sure.
>>>>>>
>>>>>> It needs a separate discussion as per me as this is a complex topic.
>>>>>>
>>>>>> If I remember correctly following are the steps
>>>>>>
>>>>>> 1. Original section is divided in to line segments.
>>>>>>
>>>>>> 2. Each line segment is offset by the amount required and
>>>>>> intersection between 2 adjacent segments are calculated. In case of concave
>>>>>> segments there would not be any intersection.
>>>>>>
>>>>>> 3. There could be global intersection of segments apart from the
>>>>>> intersection created in step 2. To calculate this it has to be quadratic.
>>>>>>
>>>>>> 4. All the points obtained in step 2 and step 3 to be added in simple
>>>>>> offset of all the original points.
>>>>>>
>>>>>> 5. create a rounded shape around each segment of the original
>>>>>> section such that the radius of the round is equal to offset required minus
>>>>>> some very small value like 0.001.
>>>>>>
>>>>>> 6. Now check if any point is inside these rounded shapes and discard
>>>>>> it.
>>>>>>
>>>>>> Balance points needs to be ordered based on the original points .
>>>>>>
>>>>>> Now, this seems to be a complicated process, but I think this is the
>>>>>> simplest way to achieve a offset.
>>>>>>
>>>>>>
>>>>>> On Sun, 3 Sept, 2023, 7:18 pm Adrian Mariano, <avm4@cornell.edu>
>>>>>> wrote:
>>>>>>
>>>>>>> Sanjeev, I don't know how you implemented offset, either in python
>>>>>>> or in OpenSCAD, but the problem I have is that checking for invalid
>>>>>>> portions of the path after doing the basic offset becomes a quadratic run
>>>>>>> time task in OpenSCAD. In other languages, it is possible to use clever
>>>>>>> data structures and I think do it in N log N. I saw an algorithm for
>>>>>>> offset that involves doing the basic offset and then keeping only the parts
>>>>>>> of the result that meet a criterion based on winding number, but the
>>>>>>> computation to partition the path into its regions and compute the winding
>>>>>>> number is very slow in OpenSCAD, again because without data structures,
>>>>>>> everything has at least quadratic run time.
>>>>>>>
>>>>>>> On Sun, Sep 3, 2023 at 9:32 AM Sanjeev Prabhakar <
>>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>>
>>>>>>>> I have observed the offset function I wrote in openscad was much
>>>>>>>> slower than the offset function written in python.
>>>>>>>>
>>>>>>>> Maybe the numpy has a lot of support and is faster. So both the
>>>>>>>> methods seem to be almost equally efficient or inefficient, whatever way
>>>>>>>> you want to look at it.
>>>>>>>>
>>>>>>>> also missed to share that the skeleton of the path extrude method
>>>>>>>> is different from the offset method.
>>>>>>>>
>>>>>>>> [image: Screenshot 2023-09-03 at 6.55.06 PM.png]
>>>>>>>>
>>>>>>>> On Sun, 3 Sept 2023 at 18:29, Adrian Mariano <avm4@cornell.edu>
>>>>>>>> wrote:
>>>>>>>>
>>>>>>>>> I think that Sanjeev has identified the two main approaches. You
>>>>>>>>> can make a rounded rectangle shape and sweep. That would look like this:
>>>>>>>>>
>>>>>>>>> include<BOSL2/std.scad>
>>>>>>>>>
>>>>>>>>> $fa=1;$fs=1;
>>>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>>>
>>>>>>>>> section = rect([Or-Ir,H], rounding=[2,2,0,0],anchor=BOT+LEFT);
>>>>>>>>> path = rect([W,L],rounding=Ir);
>>>>>>>>> path_sweep(section,path,closed=true);
>>>>>>>>>
>>>>>>>>> Note that I have chosen as the sweep path the inner rounded
>>>>>>>>> rectangle which avoids issues with self-intersection of the sweep. This is
>>>>>>>>> probably the best way to do this in terms of efficiency. Note also that
>>>>>>>>> using turtle() to compute a rounded rectangle is overkill. I only use
>>>>>>>>> turtle() for shapes that are somehow irregular.
>>>>>>>>>
>>>>>>>>> Sanjeev's second approach is to use offsetting. This is possible
>>>>>>>>> using offset_sweep(), but will likely be slower than path_sweep() because
>>>>>>>>> computing offset in userspace is slow. To do this, you have to compute the
>>>>>>>>> outside rounded shape and then subtract the inner rounded shape. So it
>>>>>>>>> could be done like this:
>>>>>>>>>
>>>>>>>>> include<BOSL2/std.scad>
>>>>>>>>> include<BOSL2/rounding.scad>
>>>>>>>>>
>>>>>>>>> $fa=1;$fs=1;
>>>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>>>
>>>>>>>>> inside = rect([W,L]-(Or-Ir)*[2,2], rounding=Ir);
>>>>>>>>> outside = rect([W,L], rounding=Or);
>>>>>>>>>
>>>>>>>>> difference(){
>>>>>>>>> offset_sweep(outside, h=H, top=os_circle(r=2));
>>>>>>>>> down(1)offset_sweep(inside, h=H+1, top=os_circle(r=-2),extra=1);
>>>>>>>>>
>>>>>>>>> }
>>>>>>>>>
>>>>>>>>> Note that you could also compute just one of inside and outside
>>>>>>>>> directly and get the other one with offset().
>>>>>>>>>
>>>>>>>>> A third way to make a shape like this is to use rounded_prism(),
>>>>>>>>> again with a difference. However, rounded_prism doesn't make circular
>>>>>>>>> roundings, so the results will be a bit different, and it will not be
>>>>>>>>> possible to assure a uniform width at the corners. (Roundovers here are
>>>>>>>>> continuous curvature beziers. The k parameter controls how gentle the
>>>>>>>>> transition, with a value of .8 close to circular. Smaller k values will
>>>>>>>>> give gentler transitions, but then large joint distance may be desired.
>>>>>>>>> Try changing k to 0.5 to see the difference.)
>>>>>>>>>
>>>>>>>>> include<BOSL2/std.scad>
>>>>>>>>> include<BOSL2/rounding.scad>
>>>>>>>>>
>>>>>>>>> $fa=1;$fs=1;
>>>>>>>>> W=34;L=60;H=10;Or = 8;Ir = 3;
>>>>>>>>>
>>>>>>>>> diff(){
>>>>>>>>> rounded_prism(rect([W,L]),height=H, joint_top=2,
>>>>>>>>> joint_sides=8,k=.8)
>>>>>>>>>
>>>>>>>>> up(.01)align(TOP,inside=true)rounded_prism(rect([W,L]-[5,5]),height=H+1,
>>>>>>>>> joint_top=-2, joint_sides=6,k=.8);
>>>>>>>>> }
>>>>>>>>>
>>>>>>>>>
>>>>>>>>> On Sun, Sep 3, 2023 at 7:18 AM Sanjeev Prabhakar <
>>>>>>>>> sprabhakar2006@gmail.com> wrote:
>>>>>>>>>
>>>>>>>>>> I will explain the process
>>>>>>>>>> I think this is important.
>>>>>>>>>>
>>>>>>>>>> There are 2 approaches.
>>>>>>>>>> 1. Extrude a section along a path
>>>>>>>>>> 2. Make a section and offset it multiple times to generate a
>>>>>>>>>> solid.
>>>>>>>>>>
>>>>>>>>>> I am sure this explanation is not enough. Will create a visual
>>>>>>>>>> description and send it to you.
>>>>>>>>>>
>>>>>>>>>> For approach 2:
>>>>>>>>>> The key is writing a function to offset a section, which I think
>>>>>>>>>> is not so easy.
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>>
>>>>>>>>>> On Sun, 3 Sept, 2023, 4:32 pm Bob Roos, <roosbob@wybatap.com>
>>>>>>>>>> wrote:
>>>>>>>>>>
>>>>>>>>>>> Hi Sanjeev,
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>> Thank you. It's beautiful, but how did you generate all those
>>>>>>>>>>> points??
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>> I had to hollow out the part a bit and change the shape some so
>>>>>>>>>>> I would like to find a more generic way to round the edges.
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>> Bob
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>> Sunday, September 3, 2023, 6:17:54 AM, you wrote:
>>>>>>>>>>>
>>>>>>>>>>> attached file
>>>>>>>>>>> [image: Screenshot 2023-09-03 at 3.45.43 PM.png]
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>> On Sun, 3 Sept 2023 at 06:50, Bob Roos <roosbob@wybatap.com>
>>>>>>>>>>> wrote:
>>>>>>>>>>>
>>>>>>>>>>>> Hello OpenSCAD,
>>>>>>>>>>>>
>>>>>>>>>>>> I want the bottom to be straight and the top inside and outside
>>>>>>>>>>>> edges to have 2mm roundover
>>>>>>>>>>>>
>>>>>>>>>>>> Thank you.
>>>>>>>>>>>>
>>>>>>>>>>>> include <BOSL2/std.scad> //or screws or threading
>>>>>>>>>>>>
>>>>>>>>>>>> W=34;
>>>>>>>>>>>> L=60;
>>>>>>>>>>>> H=10;
>>>>>>>>>>>> Or = 8;
>>>>>>>>>>>> Ir = 3;
>>>>>>>>>>>>
>>>>>>>>>>>> rect_tube(size=[W,L], wall=5, rounding=Or, h=H,irounding=3);
>>>>>>>>>>>>
>>>>>>>>>>>> --
>>>>>>>>>>>> Best regards,
>>>>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>>>>> _______________________________________________
>>>>>>>>>>>> OpenSCAD mailing list
>>>>>>>>>>>> To unsubscribe send an email to
>>>>>>>>>>>> discuss-leave@lists.openscad.org
>>>>>>>>>>>>
>>>>>>>>>>>
>>>>>>>>>>> --
>>>>>>>>>>> have Fun,
>>>>>>>>>>> Bob mailto:roosbob@wybatap.com
>>>>>>>>>>> <roosbob@wybatap.com>
>>>>>>>>>>> _______________________________________________
>>>>>>>>>>> OpenSCAD mailing list
>>>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>>>
>>>>>>>>>> _______________________________________________
>>>>>>>>>> OpenSCAD mailing list
>>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>>
>>>>>>>>> _______________________________________________
>>>>>>>>> OpenSCAD mailing list
>>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>>
>>>>>>>> _______________________________________________
>>>>>>>> OpenSCAD mailing list
>>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>>
>>>>>>> _______________________________________________
>>>>>>> OpenSCAD mailing list
>>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>