
AM
Adrian Mariano
Mon, Oct 28, 2024 9:39 PM
BOSL2 could generate the polyhedron "correctly". I don't know how hard
that would be, but that's essentially
what swapping the points does: it causes BOSL2 to build the polyhedron
the other way 'round. I don't know
enough about "skin" to know how easy it would be to detect being
backwards.
What skin() does is establish an association between points on a pair of 3d
polygons and then link the associated points together to make (part of) a
polyhedron.
I think the basic problem is determining which direction is out. I'm not
sure I know how to do that. It's easy to flip the polyhedron direction
from BOSL2. I could have skin() force 2d profiles to go a certain
direction, though that runs the risk of ruining point alignment if for some
reason the user didn't want that to happen. In other words, if you flip
one polygon but not the other one it changes the point association. I'm
not sure if there's a use-case for that or not---weird twisted
self-intersecting structures that you can preview but now render? In 3d
there's no notion of clockwise so it's not so obvious to me how to do a
similar thing with 3d inputs.
I generally make a polyhedron, check it with "thrown together" and reverse
it if it came out backwards.
On Sun, Oct 27, 2024 at 12:32 AM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
On 10/26/2024 5:44 PM, Bob Carlson wrote:
Thanks! I hear about these point ordering problems. It seems a shame one has to deal with them. Why can’t they be fixed automatically?
I don't know for sure.
There are two levels to the question here: first BOSL2 builds a
polyhedron, and then second OpenSCAD processes the polyhedron.
BOSL2 could generate the polyhedron "correctly". I don't know how hard
that would be, but that's essentially what swapping the points does: it
causes BOSL2 to build the polyhedron the other way 'round. I don't know
enough about "skin" to know how easy it would be to detect being backwards.
And then when OpenSCAD receives the "inside-out" polyhedron, it could
perhaps fix it. I think that if it's completely inside out then
detecting that and fixing it isn't hard. (But right now I'm not sure how
to tell which way is "inside".) If it's partially inside-out (like one
face is backwards) then I think I know how to detect that, and I guess
that if you can detect it then you can flip faces until they are all
consistent, and then you might be inside-out but you've reduced it to the
case above. So my not-a-geometry-wizard sense is that it's doable. (OCD
note: you need to watch out for Klein bottles, lest you flip faces
infinitely.)
Is anybody interested in spending the effort? Obviously not so far. (And
I think we can all agree that we'd rather have the geometry wizards work on
Manifold and its huge performance improvement.)
When I'm building a polyhedron, mostly I just turn on Thrown Together and
fix backward faces as required. That's less of an imposition on DIY
polyhedra than it is when your polyhedron is coming out of a library.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
> BOSL2 could generate the polyhedron "correctly". I don't know how hard
that would be, but that's essentially
> what swapping the points does: it causes BOSL2 to build the polyhedron
the other way 'round. I don't know
> enough about "skin" to know how easy it would be to detect being
backwards.
What skin() does is establish an association between points on a pair of 3d
polygons and then link the associated points together to make (part of) a
polyhedron.
I think the basic problem is determining which direction is out. I'm not
sure I know how to do that. It's easy to flip the polyhedron direction
from BOSL2. I could have skin() force 2d profiles to go a certain
direction, though that runs the risk of ruining point alignment if for some
reason the user didn't want that to happen. In other words, if you flip
one polygon but not the other one it changes the point association. I'm
not sure if there's a use-case for that or not---weird twisted
self-intersecting structures that you can preview but now render? In 3d
there's no notion of clockwise so it's not so obvious to me how to do a
similar thing with 3d inputs.
I generally make a polyhedron, check it with "thrown together" and reverse
it if it came out backwards.
On Sun, Oct 27, 2024 at 12:32 AM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
> On 10/26/2024 5:44 PM, Bob Carlson wrote:
>
> Thanks! I hear about these point ordering problems. It seems a shame one has to deal with them. Why can’t they be fixed automatically?
>
>
> I don't know for sure.
>
> There are two levels to the question here: first BOSL2 builds a
> polyhedron, and then second OpenSCAD processes the polyhedron.
>
> BOSL2 could generate the polyhedron "correctly". I don't know how hard
> that would be, but that's essentially what swapping the points does: it
> causes BOSL2 to build the polyhedron the other way 'round. I don't know
> enough about "skin" to know how easy it would be to detect being backwards.
>
> And then when OpenSCAD receives the "inside-out" polyhedron, it could
> perhaps fix it. I *think* that if it's completely inside out then
> detecting that and fixing it isn't hard. (But right now I'm not sure how
> to tell which way is "inside".) If it's partially inside-out (like one
> face is backwards) then I think I know how to detect that, and I guess
> that if you can detect it then you can flip faces until they are all
> consistent, and then you might be inside-out but you've reduced it to the
> case above. So my not-a-geometry-wizard sense is that it's doable. (OCD
> note: you need to watch out for Klein bottles, lest you flip faces
> infinitely.)
>
> Is anybody interested in spending the effort? Obviously not so far. (And
> I think we can all agree that we'd rather have the geometry wizards work on
> Manifold and its huge performance improvement.)
>
> When I'm building a polyhedron, mostly I just turn on Thrown Together and
> fix backward faces as required. That's less of an imposition on DIY
> polyhedra than it is when your polyhedron is coming out of a library.
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Tue, Oct 29, 2024 4:35 AM
So Bob, you have said you don't care about speed, which is your choice,
obviously. But for me this code is intolerably slow. Preview is useless
even after I remove the chamfering and intersection to make it have
cylindrical edges. And render takes 20s with manifold. Because the
original code was unpreviewable I couldn't easily assess how well my
rewrite matched, but it previews instantly and renders in 0.1s. (Note: a
reason I care about preview is that I can color things that I overlay to
see for example if two things match.)
Another few things. In BOSL2, global variables that start with underscore
are reserved for BOSL2 internal use, so you shouldn't be using those. You
could clobber an internal definition. (Not sure why anyone would use
variables that start with underscore as a choice---I find them very
annoying.)
The second is that I think your code measures tooth angle relative to the
vertical instead of relative to the tooth ridge. This is not the normal
way that tooth angle would be measured, e.g. on a gear. It means that
actual angle is never what you specify.
A third observation is that you should be chamfering the valleys just like
the peaks. Internal corners are stress concentration points on an object
and will weaken it. So my version can apply varying chamfers in both
places.
I personally find the rewritten code simpler than the original, as well as
much faster, and there's probably room to clean it up more. (Could
probably compute inner shape from outer with a scale() computation for
example.) It does produce a polygonal result and could be intersected
with a tube like the original to fix that if you think it's necessary. I
imagine that one intersection wouldn't be a major drag on the speed. I
agree that trying to compute the profile on a circular arc would be a
pain.
include <BOSL2/std.scad>
// Number of Teeth
_n = 36; // Number Of Teeth
// Inner Radius
_ir = 30;
// Outer Radius
_or = 50;
// Is the coupling conical?
_conic = 15;
// Tooth Profile Angle
_profile = 90; // [60, 90]
// Percentage of tooth height
_chamfer = 5; // Default 5%
_base = 1;
function basic_profile(angle,chamfer_top, chamfer_bot) =
let(
width = tan(angle/2),
pts = [
[0,(-1+chamfer_bot)width,chamfer_bot],
[0,-chamfer_topwidth,1-chamfer_top]
],
)
concat(pts, reverse(yflip(pts)));
profwidth = tan(_profile/2);
outside = _ortan(180/_n);
inside = _irtan(180/_n);
prof_out = right(_or,scale(outside/profwidth,basic_profile(_profile,
_chamfer/100, _chamfer/200)));
prof_in = right(_ir,scale(inside/profwidth,basic_profile(_profile,
_chamfer/100, _chamfer/200)));
offset = (_or-_ir) * tan(_conic);
outfull = up(offset,[for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_out)]);
infull = [for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_in)];
inbot = [for(val=infull) [val.x,val.y,-_base]];
outbot = [for(val=outfull) [val.x,val.y,-_base]];
vnf_polyhedron(vnf_vertex_array([outfull, infull, inbot, outbot],
reverse=true, col_wrap=true, row_wrap=true));
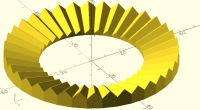
[image: image.png]
On Fri, Oct 25, 2024 at 7:45 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
I got really intrigued by the Hirth joint and have been working a library
entry that would generate them. I have it fully working, apparently,
because it renders perfectly as far as I can see. However when I load one
of the parts (a concave part) into PrusaSlicer, it reports thousands of
errors that it supposedly fixed. The visual rendering is fine, but when you
look at the slice it is completely screwed up.
First some explanation. When I looked up hirth joints I only saw flat ones
mentioned. The one I have actually encountered though is a conical one.
There is a concave part and a convex part. They fit together perfectly. I
had to invent some terminology since I did not find terms for some things I
found to be important. The outer center line is the plane that passes
through the midpoint of the teeth at the outer radius. In a flat hirth
joint all the teeth radiate from the center of this circle, call it the
origin. If the origin of the teeth is above the outer center line, then
joint has a conical shape and the two parts are concave and convex.
Each tooth at every point has the same profile, the top of the tooth
profile is either 60 or 90 degrees. The groove angle is the angle that the
groove forms from the origin to the outer radius. It will pass below (for a
convex part) the outer radius. It’s critical for making hirth joints
because it forms the tool path. The ridge angle is the angle formed by the
corresponding ridge.
If the joint is conical, then there is an inner center line that passes
through the center of the teeth at the inner radius. The tooth height is
the critical number to calculate. It is dependent on the number of teeth,
the profile angle and the inner and out radii. Something that really
complicates the mental gymnastics is that the tooth height is smaller at
the inner radius. My code adds a “base” of extra material at the bottom of
the convex part and the top of the concave part. What’s tricky is
positioning the base of the concave part relative to the inner center line.
The concave parts base is relatively easy to place because it depends on
the outer radius and center line.
I generate the raw teeth using the groove and ridge angles and spherical
coordinates to make two 2d tooth profiles. Then I complete a tooth using
skin(). A for loop generates the full set of N teeth. Then intersection or
difference is used the trim the teeth at the inner and outer radii. I
discovered something at that point, but solved it pretty simply. When
diffing a cylinder from the N teeth, each tooth took up a small portion of
the cylinder being diffed out. I had to raise the $fn on the cylinder or
tube being used so that I got enough points in each tooth that diff or
intersection was accurate. I kept raising it until the results stopped
improving. I ended up with the 16*360 you see in the code.
After I have the raw teeth, I generate a cone that is diffed away to
produce the chamfer at the top of the teeth. Then I add in the base. The
base also adds the “chamfer” at the bottom of the groove. It’s half the
size of the top chamfer to leave a little gap when the parts are joined.
When I comment out the everything but the raw teeth and import the STL
into PrusaSlicer, it reports errors fixed, but appears to slice correctly
when supports are added.
When I add the intersection to trim the raw teeth, the number of reported
errors goes way up.
When I add the diff to remove the chamfer, the number goes way up again.
When I add in the base, the number goes up again and it starts reporting
many open edges.
Throughout, OpenSCAD reports no errors. Using $fn at 16360, manifold
renders in 4+ seconds. At 32360, it’s 53+ seconds. I did check CSG and it
did not help.
Maybe the biggest hint is that the convex part uses almost identical code,
but produces no errors. Very weird.
So, is this an OpenSCAD problem? Or something in my code?
It’s also possible that my math is off somewhere. My formal trig training
was 60 years ago. However I doubt a math error is responsible for the
slicing problem and STL errors.
-Bob
include <BOSL2/std.scad>
include <BOSL2/structs.scad>
// Number of Teeth
_n = 36; // Number Of Teeth
// Inner Radius
_ir = 30;
// Outer Radius
_or = 50;
// Is the coupling conical?
_conic = 10;
// Tooth Profile Angle
_profile = 60; // [60, 90]
// Percentage of tooth height
_chamfer = 5; // Default 5%
_base = 1;
$fn = 180;
tiny = 1 / 1024;
hirth_concave();
_irRatio = _ir / _or;
_toothAngle = 360/_n;
_toothHeight = (sin(_toothAngle/2) * _or) / tan(_profile/2);
_chamferHeight = _chamfer * _toothHeight / 100;
_grooveAngle = atan(((_toothHeight/2) + _conic) / _or);
_ridgeAngle = -atan(((_toothHeight/2) - _conic) / _or);
_innerCenterLine = (1 - _irRatio) * _conic;
_stackHeight = _innerCenterLine + _toothHeight + 2*_base;
_tubeHeight = 2*_conic + 2*_base + 2*_toothHeight;
module hirth_concave() {
zrot(_toothAngle/2)
union() {
difference() {
intersection() {
union() {
for (i = [0 : 360/_n : 359])
zrot(i)
_profileF();
}
tube(ir = _ir, or = _or, anchor = CENTER, l = _tubeHeight,
orient = UP, $fn = 16360);
}
_chamferF();
zcyl(r = _ir, h = _tubeHeight, $fn = 16360, anchor = CENTER);
}
_baseF();
}
} // hirth_concave
module _profileF() {
IR = _ir * .5;
OR = _or * 1.5;
tI = [spherical_to_xyz(IR, 0, _grooveAngle + 90),
spherical_to_xyz(IR, _toothAngle/2, _ridgeAngle + 90),
spherical_to_xyz(IR, -_toothAngle/2, _ridgeAngle + 90)];
tO = [spherical_to_xyz(OR, 0, _grooveAngle + 90),
spherical_to_xyz(OR, _toothAngle/2, _ridgeAngle + 90),
spherical_to_xyz(OR, -_toothAngle/2, _ridgeAngle + 90)];
up(_conic)
skin([tI, tO], slices = 0);
}
module _chamferF() {
A = -_toothHeight/2 - .1;
B = -_toothHeight/2 + _chamferHeight;
pts = [[0, _conic],
[_or+tiny, A],
[_or+tiny, B]];
rotate_extrude(angle = 360, $fn = 16*360)
polygon(pts);
}
module _baseF() {
A = _base + _irRatio*_toothHeight/2 + _innerCenterLine;
B = _irRatio * (_toothHeight/2 - _chamferHeight/2) + _innerCenterLine;
C = _toothHeight/2 - _chamferHeight/2;
pts = [
[_ir, A],
[_ir, B],
[_or, C],
[_or, A]
];
rotate_extrude(angle = 360, $fn = 360*16)
polygon(pts);
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
So Bob, you have said you don't care about speed, which is your choice,
obviously. But for me this code is intolerably slow. Preview is useless
even after I remove the chamfering and intersection to make it have
cylindrical edges. And render takes 20s with manifold. Because the
original code was unpreviewable I couldn't easily assess how well my
rewrite matched, but it previews instantly and renders in 0.1s. (Note: a
reason I care about preview is that I can color things that I overlay to
see for example if two things match.)
Another few things. In BOSL2, global variables that start with underscore
are reserved for BOSL2 internal use, so you shouldn't be using those. You
could clobber an internal definition. (Not sure why anyone would use
variables that start with underscore as a choice---I find them very
annoying.)
The second is that I think your code measures tooth angle relative to the
vertical instead of relative to the tooth ridge. This is not the normal
way that tooth angle would be measured, e.g. on a gear. It means that
actual angle is never what you specify.
A third observation is that you should be chamfering the valleys just like
the peaks. Internal corners are stress concentration points on an object
and will weaken it. So my version can apply varying chamfers in both
places.
I personally find the rewritten code simpler than the original, as well as
much faster, and there's probably room to clean it up more. (Could
probably compute inner shape from outer with a scale() computation for
example.) It does produce a polygonal result and could be intersected
with a tube like the original to fix that if you think it's necessary. I
imagine that one intersection wouldn't be a major drag on the speed. I
agree that trying to compute the profile on a circular arc would be a
pain.
include <BOSL2/std.scad>
// Number of Teeth
_n = 36; // Number Of Teeth
// Inner Radius
_ir = 30;
// Outer Radius
_or = 50;
// Is the coupling conical?
_conic = 15;
// Tooth Profile Angle
_profile = 90; // [60, 90]
// Percentage of tooth height
_chamfer = 5; // Default 5%
_base = 1;
function basic_profile(angle,chamfer_top, chamfer_bot) =
let(
width = tan(angle/2),
pts = [
[0,(-1+chamfer_bot)*width,chamfer_bot],
[0,-chamfer_top*width,1-chamfer_top]
],
)
concat(pts, reverse(yflip(pts)));
profwidth = tan(_profile/2);
outside = _or*tan(180/_n);
inside = _ir*tan(180/_n);
prof_out = right(_or,scale(outside/profwidth,basic_profile(_profile,
_chamfer/100, _chamfer/200)));
prof_in = right(_ir,scale(inside/profwidth,basic_profile(_profile,
_chamfer/100, _chamfer/200)));
offset = (_or-_ir) * tan(_conic);
outfull = up(offset,[for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_out)]);
infull = [for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_in)];
inbot = [for(val=infull) [val.x,val.y,-_base]];
outbot = [for(val=outfull) [val.x,val.y,-_base]];
vnf_polyhedron(vnf_vertex_array([outfull, infull, inbot, outbot],
reverse=true, col_wrap=true, row_wrap=true));
[image: image.png]
On Fri, Oct 25, 2024 at 7:45 PM Bob Carlson via Discuss <
discuss@lists.openscad.org> wrote:
> I got really intrigued by the Hirth joint and have been working a library
> entry that would generate them. I have it fully working, apparently,
> because it renders perfectly as far as I can see. However when I load one
> of the parts (a concave part) into PrusaSlicer, it reports thousands of
> errors that it supposedly fixed. The visual rendering is fine, but when you
> look at the slice it is completely screwed up.
>
> First some explanation. When I looked up hirth joints I only saw flat ones
> mentioned. The one I have actually encountered though is a conical one.
> There is a concave part and a convex part. They fit together perfectly. I
> had to invent some terminology since I did not find terms for some things I
> found to be important. The outer center line is the plane that passes
> through the midpoint of the teeth at the outer radius. In a flat hirth
> joint all the teeth radiate from the center of this circle, call it the
> origin. If the origin of the teeth is above the outer center line, then
> joint has a conical shape and the two parts are concave and convex.
>
> Each tooth at every point has the same profile, the top of the tooth
> profile is either 60 or 90 degrees. The groove angle is the angle that the
> groove forms from the origin to the outer radius. It will pass below (for a
> convex part) the outer radius. It’s critical for making hirth joints
> because it forms the tool path. The ridge angle is the angle formed by the
> corresponding ridge.
>
> If the joint is conical, then there is an inner center line that passes
> through the center of the teeth at the inner radius. The tooth height is
> the critical number to calculate. It is dependent on the number of teeth,
> the profile angle and the inner and out radii. Something that really
> complicates the mental gymnastics is that the tooth height is smaller at
> the inner radius. My code adds a “base” of extra material at the bottom of
> the convex part and the top of the concave part. What’s tricky is
> positioning the base of the concave part relative to the inner center line.
> The concave parts base is relatively easy to place because it depends on
> the outer radius and center line.
>
> I generate the raw teeth using the groove and ridge angles and spherical
> coordinates to make two 2d tooth profiles. Then I complete a tooth using
> skin(). A for loop generates the full set of N teeth. Then intersection or
> difference is used the trim the teeth at the inner and outer radii. I
> discovered something at that point, but solved it pretty simply. When
> diffing a cylinder from the N teeth, each tooth took up a small portion of
> the cylinder being diffed out. I had to raise the $fn on the cylinder or
> tube being used so that I got enough points in each tooth that diff or
> intersection was accurate. I kept raising it until the results stopped
> improving. I ended up with the 16*360 you see in the code.
>
> After I have the raw teeth, I generate a cone that is diffed away to
> produce the chamfer at the top of the teeth. Then I add in the base. The
> base also adds the “chamfer” at the bottom of the groove. It’s half the
> size of the top chamfer to leave a little gap when the parts are joined.
>
> When I comment out the everything but the raw teeth and import the STL
> into PrusaSlicer, it reports errors fixed, but appears to slice correctly
> when supports are added.
>
> When I add the intersection to trim the raw teeth, the number of reported
> errors goes way up.
>
> When I add the diff to remove the chamfer, the number goes way up again.
>
> When I add in the base, the number goes up again and it starts reporting
> many open edges.
>
> Throughout, OpenSCAD reports no errors. Using $fn at 16*360, manifold
> renders in 4+ seconds. At 32*360, it’s 53+ seconds. I did check CSG and it
> did not help.
>
> Maybe the biggest hint is that the convex part uses almost identical code,
> but produces no errors. Very weird.
>
> So, is this an OpenSCAD problem? Or something in my code?
>
> It’s also possible that my math is off somewhere. My formal trig training
> was 60 years ago. However I doubt a math error is responsible for the
> slicing problem and STL errors.
>
> -Bob
>
>
> include <BOSL2/std.scad>
> include <BOSL2/structs.scad>
>
> // Number of Teeth
> _n = 36; // Number Of Teeth
>
> // Inner Radius
> _ir = 30;
> // Outer Radius
> _or = 50;
> // Is the coupling conical?
> _conic = 10;
> // Tooth Profile Angle
> _profile = 60; // [60, 90]
> // Percentage of tooth height
> _chamfer = 5; // Default 5%
> _base = 1;
>
> $fn = 180;
> tiny = 1 / 1024;
>
> hirth_concave();
>
> _irRatio = _ir / _or;
> _toothAngle = 360/_n;
> _toothHeight = (sin(_toothAngle/2) * _or) / tan(_profile/2);
> _chamferHeight = _chamfer * _toothHeight / 100;
> _grooveAngle = atan(((_toothHeight/2) + _conic) / _or);
> _ridgeAngle = -atan(((_toothHeight/2) - _conic) / _or);
> _innerCenterLine = (1 - _irRatio) * _conic;
> _stackHeight = _innerCenterLine + _toothHeight + 2*_base;
> _tubeHeight = 2*_conic + 2*_base + 2*_toothHeight;
>
> module hirth_concave() {
> zrot(_toothAngle/2)
> union() {
> difference() {
> intersection() {
> union() {
> for (i = [0 : 360/_n : 359])
> zrot(i)
> _profileF();
> }
> tube(ir = _ir, or = _or, anchor = CENTER, l = _tubeHeight,
> orient = UP, $fn = 16*360);
> }
> _chamferF();
> zcyl(r = _ir, h = _tubeHeight, $fn = 16*360, anchor = CENTER);
> }
> _baseF();
> }
> } // hirth_concave
>
> module _profileF() {
> IR = _ir * .5;
> OR = _or * 1.5;
> tI = [spherical_to_xyz(IR, 0, _grooveAngle + 90),
> spherical_to_xyz(IR, _toothAngle/2, _ridgeAngle + 90),
> spherical_to_xyz(IR, -_toothAngle/2, _ridgeAngle + 90)];
>
> tO = [spherical_to_xyz(OR, 0, _grooveAngle + 90),
> spherical_to_xyz(OR, _toothAngle/2, _ridgeAngle + 90),
> spherical_to_xyz(OR, -_toothAngle/2, _ridgeAngle + 90)];
> up(_conic)
> skin([tI, tO], slices = 0);
> }
>
>
> module _chamferF() {
> A = -_toothHeight/2 - .1;
> B = -_toothHeight/2 + _chamferHeight;
>
> pts = [[0, _conic],
> [_or+tiny, A],
> [_or+tiny, B]];
>
> rotate_extrude(angle = 360, $fn = 16*360)
> polygon(pts);
> }
>
> module _baseF() {
> A = _base + _irRatio*_toothHeight/2 + _innerCenterLine;
> B = _irRatio * (_toothHeight/2 - _chamferHeight/2) + _innerCenterLine;
> C = _toothHeight/2 - _chamferHeight/2;
> pts = [
> [_ir, A],
> [_ir, B],
> [_or, C],
> [_or, A]
> ];
>
> rotate_extrude(angle = 360, $fn = 360*16)
> polygon(pts);
> }
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

M
mikeonenine@web.de
Wed, Oct 30, 2024 12:53 AM
The second is that I think your code measures tooth angle relative to the
vertical instead of relative to the tooth ridge. This is not the normal
way that tooth angle would be measured, e.g. on a gear. It means that
actual angle is never what you specify.
A third observation is that you should be chamfering the valleys just like
the peaks. Internal corners are stress concentration points on an object
and will weaken it. So my version can apply varying chamfers in both
places.
Machining or grinding would produce flat peaks, forging might produce more rounded peaks. What is best for 3D printing? The code below gives a choice.
The valleys are best rounded to avoid stress concentrations.
A polygon is linear_extruded to give a spline:
r=100; // Radius outer
n=30; // No. of splines
rr=4; // Radius ridge
rv=1.5; // Radius valley
f=2; // Flat
a=60; // Angle between flanks
c=-20; // Conicity
function angle() = 90-a/2;
aa=angle();
function base() = r*tan(360/n/2);
b=base();
$fn=500;
module fspline()
{
translate([0,0,-r])
linear_extrude(r, scale=[0 ,0],convexity=3)
translate([0,-b*tan(aa)/2+c])
polygon([
/*
// Rounded ridge
for(i=[-60:60])
[rr*sin(i), rr*cos(i)+b*tan(a)-2*rr],
*/
// alternatively:
// Flat ridge
[-f/tan(aa), b*tan(aa)-f],
[f/tan(aa), b*tan(aa)-f],
for(i=[180:120-(60-a)/2])
[b+rv*sin(-i), rv*cos(-i)+rv/sin(a/2)],
[b, 0],
[-b, 0],
for(i=[180:240+(60-a)/2])
[-b+rv*sin(-i), rv*cos(-i)+rv/sin(a/2)],
]);
}
// Test spline
fspline();
Multiple splines are then arranged in a circle:
for(i=[1:n])
rotate([90,0,i*360/n])
The rest is just an intersection with a cylinder to round the splines and a hole in the middle.
Later versions of OpenSCAD seem to need a union() at some point for the above to work and i am not sure how it would print - I read somewhere that parts have to overlap slightly, to print as a whole.
Adrian Mariano wrote:
> The second is that I think your code measures tooth angle relative to the
> vertical instead of relative to the tooth ridge. This is not the normal
> way that tooth angle would be measured, e.g. on a gear. It means that
> actual angle is never what you specify.
>
> A third observation is that you should be chamfering the valleys just like
> the peaks. Internal corners are stress concentration points on an object
> and will weaken it. So my version can apply varying chamfers in both
> places.
Machining or grinding would produce flat peaks, forging might produce more rounded peaks. What is best for 3D printing? The code below gives a choice.
The valleys are best rounded to avoid stress concentrations.
A polygon is linear_extruded to give a spline:
`r=100; // Radius outer`
`n=30; // No. of splines`
`rr=4; // Radius ridge`
`rv=1.5; // Radius valley `
`f=2; // Flat `
`a=60; // Angle between flanks`
`c=-20; // Conicity`
`function angle() = 90-a/2;`
`aa=angle();`
`function base() = r*tan(360/n/2);`
`b=base();`
`$fn=500;`
`module fspline()`
`{`
`translate([0,0,-r])`
`linear_extrude(r, scale=[0 ,0],convexity=3)`
`translate([0,-b*tan(aa)/2+c])`
`polygon([`
`/*`
`// Rounded ridge`
`for(i=[-60:60])`
`[rr*sin(i), rr*cos(i)+b*tan(a)-2*rr],`
`*/`
`// alternatively:`
`// Flat ridge`
`[-f/tan(aa), b*tan(aa)-f],`
`[f/tan(aa), b*tan(aa)-f],`
`for(i=[180:120-(60-a)/2])`
`[b+rv*sin(-i), rv*cos(-i)+rv/sin(a/2)],`
`[b, 0],`
`[-b, 0],`
`for(i=[180:240+(60-a)/2])`
`[-b+rv*sin(-i), rv*cos(-i)+rv/sin(a/2)],`
`]);`
`}`
`// Test spline`
`fspline();`
Multiple splines are then arranged in a circle:
`for(i=[1:n])`
`rotate([90,0,i*360/n])`
The rest is just an intersection with a cylinder to round the splines and a hole in the middle.
Later versions of OpenSCAD seem to need a union() at some point for the above to work and i am not sure how it would print - I read somewhere that parts have to overlap slightly, to print as a whole.

BC
Bob Carlson
Thu, Oct 31, 2024 1:33 AM
On Oct 26, 2024, at 16:21, Jordan Brown openscad@jordan.maileater.net wrote:
Also, a tidbit: _chamferF() generates a conical figure that might as well be a cone.
up(_conic + _chamferHeight) scale(1.5) zcyl(h = _toothHeight/2 + _conic, r1 = _or, r2 = 0, anchor=TOP);
Since it's anchored at the top, I didn't have to fiddle with making sure that it was slightly larger than the thing it's cutting from and could just scale it up a bit.
When I tried switching to a cone rather than rotate_extrude, the rendering time went up by about 50% (roughly a quarter second to .4 seconds). So, I’ve kept the current code.
-Bob
> On Oct 26, 2024, at 16:21, Jordan Brown <openscad@jordan.maileater.net> wrote:
>
> Also, a tidbit: _chamferF() generates a conical figure that might as well be a cone.
> up(_conic + _chamferHeight) scale(1.5) zcyl(h = _toothHeight/2 + _conic, r1 = _or, r2 = 0, anchor=TOP);
> Since it's anchored at the top, I didn't have to fiddle with making sure that it was slightly larger than the thing it's cutting from and could just scale it up a bit.
When I tried switching to a cone rather than rotate_extrude, the rendering time went up by about 50% (roughly a quarter second to .4 seconds). So, I’ve kept the current code.
-Bob

BC
Bob Carlson
Thu, Oct 31, 2024 1:51 AM
The current code renders 1 part in about 0.25 s, so I doubt you would have much problem with the current performance.
As it happens, I switched to using _name's in the code because I will be offering it for inclusion in BOSL2. It’s also good for use in my own library if that’s where it stays. I have full attachability working now and the output looks very good.
The valleys are chamfered too, at 50% of the ridge chamfer size so a proper gap is left when the parts are together. If you look closely you can see it in the demo code too.
There are 3 angles I calculate. Tooth Angle is the angle between teeth radially. It’s simple, 360/N. The other two are the groove angle and ridge angle. These are calculated relative to horizontal. In a flat hirth joint, they are plus and minus the same number. In a conical joint, it’s different, but still measured relative to the XY plane. When I use them in the code I believe it’s always in a call to a spherical transform. In those calls 0 degrees is vertical, so I have to add 90.
Adding the “bases” and getting the chamfers right in the conical cases was REALLY tricky. It’s the conical parts that cause all the problems.
You should see the finished code in an enhancement request to BOSL2 in a few days.
-Bob
On Oct 28, 2024, at 21:35, Adrian Mariano avm4@cornell.edu wrote:
So Bob, you have said you don't care about speed, which is your choice, obviously. But for me this code is intolerably slow. Preview is useless even after I remove the chamfering and intersection to make it have cylindrical edges. And render takes 20s with manifold. Because the original code was unpreviewable I couldn't easily assess how well my rewrite matched, but it previews instantly and renders in 0.1s. (Note: a reason I care about preview is that I can color things that I overlay to see for example if two things match.)
Another few things. In BOSL2, global variables that start with underscore are reserved for BOSL2 internal use, so you shouldn't be using those. You could clobber an internal definition. (Not sure why anyone would use variables that start with underscore as a choice---I find them very annoying.)
The second is that I think your code measures tooth angle relative to the vertical instead of relative to the tooth ridge. This is not the normal way that tooth angle would be measured, e.g. on a gear. It means that actual angle is never what you specify.
A third observation is that you should be chamfering the valleys just like the peaks. Internal corners are stress concentration points on an object and will weaken it. So my version can apply varying chamfers in both places.
I personally find the rewritten code simpler than the original, as well as much faster, and there's probably room to clean it up more. (Could probably compute inner shape from outer with a scale() computation for example.) It does produce a polygonal result and could be intersected with a tube like the original to fix that if you think it's necessary. I imagine that one intersection wouldn't be a major drag on the speed. I agree that trying to compute the profile on a circular arc would be a pain.
include <BOSL2/std.scad>
// Number of Teeth
_n = 36; // Number Of Teeth
// Inner Radius
_ir = 30;
// Outer Radius
_or = 50;
// Is the coupling conical?
_conic = 15;
// Tooth Profile Angle
_profile = 90; // [60, 90]
// Percentage of tooth height
_chamfer = 5; // Default 5%
_base = 1;
function basic_profile(angle,chamfer_top, chamfer_bot) =
let(
width = tan(angle/2),
pts = [
[0,(-1+chamfer_bot)width,chamfer_bot],
[0,-chamfer_topwidth,1-chamfer_top]
],
)
concat(pts, reverse(yflip(pts)));
profwidth = tan(_profile/2);
outside = _ortan(180/_n);
inside = _irtan(180/_n);
prof_out = right(_or,scale(outside/profwidth,basic_profile(_profile, _chamfer/100, _chamfer/200)));
prof_in = right(_ir,scale(inside/profwidth,basic_profile(_profile, _chamfer/100, _chamfer/200)));
offset = (_or-_ir) * tan(_conic);
outfull = up(offset,[for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_out)]);
infull = [for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_in)];
inbot = [for(val=infull) [val.x,val.y,-_base]];
outbot = [for(val=outfull) [val.x,val.y,-_base]];
vnf_polyhedron(vnf_vertex_array([outfull, infull, inbot, outbot], reverse=true, col_wrap=true, row_wrap=true));
<image.png>
The current code renders 1 part in about 0.25 s, so I doubt you would have much problem with the current performance.
As it happens, I switched to using _name's in the code because I will be offering it for inclusion in BOSL2. It’s also good for use in my own library if that’s where it stays. I have full attachability working now and the output looks very good.
The valleys are chamfered too, at 50% of the ridge chamfer size so a proper gap is left when the parts are together. If you look closely you can see it in the demo code too.
There are 3 angles I calculate. Tooth Angle is the angle between teeth radially. It’s simple, 360/N. The other two are the groove angle and ridge angle. These are calculated relative to horizontal. In a flat hirth joint, they are plus and minus the same number. In a conical joint, it’s different, but still measured relative to the XY plane. When I use them in the code I believe it’s always in a call to a spherical transform. In those calls 0 degrees is vertical, so I have to add 90.
Adding the “bases” and getting the chamfers right in the conical cases was REALLY tricky. It’s the conical parts that cause all the problems.
You should see the finished code in an enhancement request to BOSL2 in a few days.
-Bob
> On Oct 28, 2024, at 21:35, Adrian Mariano <avm4@cornell.edu> wrote:
>
> So Bob, you have said you don't care about speed, which is your choice, obviously. But for me this code is intolerably slow. Preview is useless even after I remove the chamfering and intersection to make it have cylindrical edges. And render takes 20s with manifold. Because the original code was unpreviewable I couldn't easily assess how well my rewrite matched, but it previews instantly and renders in 0.1s. (Note: a reason I care about preview is that I can color things that I overlay to see for example if two things match.)
>
> Another few things. In BOSL2, global variables that start with underscore are reserved for BOSL2 internal use, so you shouldn't be using those. You could clobber an internal definition. (Not sure why anyone would use variables that start with underscore as a choice---I find them very annoying.)
>
> The second is that I think your code measures tooth angle relative to the vertical instead of relative to the tooth ridge. This is not the normal way that tooth angle would be measured, e.g. on a gear. It means that actual angle is never what you specify.
>
> A third observation is that you should be chamfering the valleys just like the peaks. Internal corners are stress concentration points on an object and will weaken it. So my version can apply varying chamfers in both places.
>
> I personally find the rewritten code simpler than the original, as well as much faster, and there's probably room to clean it up more. (Could probably compute inner shape from outer with a scale() computation for example.) It does produce a polygonal result and could be intersected with a tube like the original to fix that if you think it's necessary. I imagine that one intersection wouldn't be a major drag on the speed. I agree that trying to compute the profile on a circular arc would be a pain.
>
> include <BOSL2/std.scad>
>
> // Number of Teeth
> _n = 36; // Number Of Teeth
>
> // Inner Radius
> _ir = 30;
> // Outer Radius
> _or = 50;
> // Is the coupling conical?
> _conic = 15;
> // Tooth Profile Angle
> _profile = 90; // [60, 90]
> // Percentage of tooth height
> _chamfer = 5; // Default 5%
> _base = 1;
>
> function basic_profile(angle,chamfer_top, chamfer_bot) =
> let(
> width = tan(angle/2),
> pts = [
> [0,(-1+chamfer_bot)*width,chamfer_bot],
> [0,-chamfer_top*width,1-chamfer_top]
> ],
> )
> concat(pts, reverse(yflip(pts)));
>
> profwidth = tan(_profile/2);
> outside = _or*tan(180/_n);
> inside = _ir*tan(180/_n);
>
> prof_out = right(_or,scale(outside/profwidth,basic_profile(_profile, _chamfer/100, _chamfer/200)));
> prof_in = right(_ir,scale(inside/profwidth,basic_profile(_profile, _chamfer/100, _chamfer/200)));
>
> offset = (_or-_ir) * tan(_conic);
>
> outfull = up(offset,[for(i=lerpn(0,360,_n,endpoint=false))
> each zrot(i,prof_out)]);
> infull = [for(i=lerpn(0,360,_n,endpoint=false))
> each zrot(i,prof_in)];
>
> inbot = [for(val=infull) [val.x,val.y,-_base]];
> outbot = [for(val=outfull) [val.x,val.y,-_base]];
>
> vnf_polyhedron(vnf_vertex_array([outfull, infull, inbot, outbot], reverse=true, col_wrap=true, row_wrap=true));
>
> <image.png>
>
>
>
>
>

AM
Adrian Mariano
Thu, Oct 31, 2024 3:21 AM
The only angles that really are needed to make this are the angle of
the teeth and one additional angle, the angle of the ridge line or the
tooth base (including any conical angle). I'm not sure how that angle
is best defined. Maybe it's different for the two halves of the joint?
Computing a bunch of other angles does not appear to be necessary,
though maybe for figuring out how to adjust the tooth angle you need
an extra computation.
I think the tooth angle should be defined relative to the top line
of the teeth (ridge line?), but your code defines it relative to
absolute vertical, so as you change the conical angle the tooth angle
changes. And if the conical angle is zero the tooth angle is not the
specified
angle. At least that appeared to be the case with the version you
posted.
When you organize the computation the way I did in my posted example
the chamfers are trivial regardless of the angle of anything, though if you
want to get the tooth angle relative to the ridge line some care is
required.
Did you look at how I did it? Using roundings instead of chamfers might
be nice too, especially for joints at larger scale. I guess another
question
is whether chamfers should be absolute values rather than proportional
to tooth size.
In BOSL2 the undercores are used only for private globals, and all the
global variables you have should actually be parameters in a library
implementation. I mean, there's no harm in using underscores
internally; I just find them annoying and hard to read. One reason to
use them for internals is that nobody in their right mind would CHOOSE
to prefix their variables with them. :)
How fast does your existing code preview? Because the preview
performance of the code I tried made preview unusable, even when I
removed the chamfers and intersection with the tube. I assumed this
was the result of having 36 objects unioned together, though even so
it seemed oddly sluggish. I also noticed that intersecting with a tube
produces a potential issue: the $fn for the tube needs to be a multiple
of the tooth count, or the result looks funny.
The Hirth joint looks interesting and useful so I think we'll get it
into BOSL2 one way or another. Do you use this joint by gluing at
the joint? Or by holding parts captive somehow so that shafts are
locked at the joint?
On Wed, Oct 30, 2024 at 9:52 PM Bob Carlson bob@rjcarlson.com wrote:
The current code renders 1 part in about 0.25 s, so I doubt you would have
much problem with the current performance.
As it happens, I switched to using _name's in the code because I will be
offering it for inclusion in BOSL2. It’s also good for use in my own
library if that’s where it stays. I have full attachability working now and
the output looks very good.
The valleys are chamfered too, at 50% of the ridge chamfer size so a
proper gap is left when the parts are together. If you look closely you can
see it in the demo code too.
There are 3 angles I calculate. Tooth Angle is the angle between teeth
radially. It’s simple, 360/N. The other two are the groove angle and ridge
angle. These are calculated relative to horizontal. In a flat hirth joint,
they are plus and minus the same number. In a conical joint, it’s
different, but still measured relative to the XY plane. When I use them in
the code I believe it’s always in a call to a spherical transform. In those
calls 0 degrees is vertical, so I have to add 90.
Adding the “bases” and getting the chamfers right in the conical cases was
REALLY tricky. It’s the conical parts that cause all the problems.
You should see the finished code in an enhancement request to BOSL2 in a
few days.
-Bob
On Oct 28, 2024, at 21:35, Adrian Mariano avm4@cornell.edu wrote:
So Bob, you have said you don't care about speed, which is your choice,
obviously. But for me this code is intolerably slow. Preview is useless
even after I remove the chamfering and intersection to make it have
cylindrical edges. And render takes 20s with manifold. Because the
original code was unpreviewable I couldn't easily assess how well my
rewrite matched, but it previews instantly and renders in 0.1s. (Note: a
reason I care about preview is that I can color things that I overlay to
see for example if two things match.)
Another few things. In BOSL2, global variables that start with
underscore are reserved for BOSL2 internal use, so you shouldn't be using
those. You could clobber an internal definition. (Not sure why anyone
would use variables that start with underscore as a choice---I find them
very annoying.)
The second is that I think your code measures tooth angle relative to
the vertical instead of relative to the tooth ridge. This is not the
normal way that tooth angle would be measured, e.g. on a gear. It means
that actual angle is never what you specify.
A third observation is that you should be chamfering the valleys just
like the peaks. Internal corners are stress concentration points on an
object and will weaken it. So my version can apply varying chamfers in
both places.
I personally find the rewritten code simpler than the original, as well
as much faster, and there's probably room to clean it up more. (Could
probably compute inner shape from outer with a scale() computation for
example.) It does produce a polygonal result and could be intersected
with a tube like the original to fix that if you think it's necessary. I
imagine that one intersection wouldn't be a major drag on the speed. I
agree that trying to compute the profile on a circular arc would be a pain.
include <BOSL2/std.scad>
// Number of Teeth
_n = 36; // Number Of Teeth
// Inner Radius
_ir = 30;
// Outer Radius
_or = 50;
// Is the coupling conical?
_conic = 15;
// Tooth Profile Angle
_profile = 90; // [60, 90]
// Percentage of tooth height
_chamfer = 5; // Default 5%
_base = 1;
function basic_profile(angle,chamfer_top, chamfer_bot) =
let(
width = tan(angle/2),
pts = [
[0,(-1+chamfer_bot)width,chamfer_bot],
[0,-chamfer_topwidth,1-chamfer_top]
],
)
concat(pts, reverse(yflip(pts)));
profwidth = tan(_profile/2);
outside = _ortan(180/_n);
inside = _irtan(180/_n);
prof_out = right(_or,scale(outside/profwidth,basic_profile(_profile,
_chamfer/100, _chamfer/200)));
prof_in = right(_ir,scale(inside/profwidth,basic_profile(_profile,
_chamfer/100, _chamfer/200)));
offset = (_or-_ir) * tan(_conic);
outfull = up(offset,[for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_out)]);
infull = [for(i=lerpn(0,360,_n,endpoint=false))
each zrot(i,prof_in)];
inbot = [for(val=infull) [val.x,val.y,-_base]];
outbot = [for(val=outfull) [val.x,val.y,-_base]];
vnf_polyhedron(vnf_vertex_array([outfull, infull, inbot, outbot],
reverse=true, col_wrap=true, row_wrap=true));
The only angles that really are needed to make this are the angle of
the teeth and one additional angle, the angle of the ridge line or the
tooth base (including any conical angle). I'm not sure how that angle
is best defined. Maybe it's different for the two halves of the joint?
Computing a bunch of other angles does not appear to be necessary,
though maybe for figuring out how to adjust the tooth angle you need
an extra computation.
I think the tooth angle *should* be defined relative to the top line
of the teeth (ridge line?), but your code defines it relative to
absolute vertical, so as you change the conical angle the tooth angle
changes. And if the conical angle is zero the tooth angle is not the
specified
angle. At least that appeared to be the case with the version you
posted.
When you organize the computation the way I did in my posted example
the chamfers are trivial regardless of the angle of anything, though if you
want to get the tooth angle relative to the ridge line some care is
required.
Did you look at how I did it? Using roundings instead of chamfers might
be nice too, especially for joints at larger scale. I guess another
question
is whether chamfers should be absolute values rather than proportional
to tooth size.
In BOSL2 the undercores are used only for private globals, and all the
global variables you have should actually be parameters in a library
implementation. I mean, there's no harm in using underscores
internally; I just find them annoying and hard to read. One reason to
use them for internals is that nobody in their right mind would CHOOSE
to prefix their variables with them. :)
How fast does your existing code preview? Because the preview
performance of the code I tried made preview unusable, even when I
removed the chamfers and intersection with the tube. I assumed this
was the result of having 36 objects unioned together, though even so
it seemed oddly sluggish. I also noticed that intersecting with a tube
produces a potential issue: the $fn for the tube needs to be a multiple
of the tooth count, or the result looks funny.
The Hirth joint looks interesting and useful so I think we'll get it
into BOSL2 one way or another. Do you use this joint by gluing at
the joint? Or by holding parts captive somehow so that shafts are
locked at the joint?
On Wed, Oct 30, 2024 at 9:52 PM Bob Carlson <bob@rjcarlson.com> wrote:
> The current code renders 1 part in about 0.25 s, so I doubt you would have
> much problem with the current performance.
>
> As it happens, I switched to using _name's in the code because I will be
> offering it for inclusion in BOSL2. It’s also good for use in my own
> library if that’s where it stays. I have full attachability working now and
> the output looks very good.
>
> The valleys are chamfered too, at 50% of the ridge chamfer size so a
> proper gap is left when the parts are together. If you look closely you can
> see it in the demo code too.
>
> There are 3 angles I calculate. Tooth Angle is the angle between teeth
> radially. It’s simple, 360/N. The other two are the groove angle and ridge
> angle. These are calculated relative to horizontal. In a flat hirth joint,
> they are plus and minus the same number. In a conical joint, it’s
> different, but still measured relative to the XY plane. When I use them in
> the code I believe it’s always in a call to a spherical transform. In those
> calls 0 degrees is vertical, so I have to add 90.
>
> Adding the “bases” and getting the chamfers right in the conical cases was
> REALLY tricky. It’s the conical parts that cause all the problems.
>
> You should see the finished code in an enhancement request to BOSL2 in a
> few days.
>
> -Bob
>
> > On Oct 28, 2024, at 21:35, Adrian Mariano <avm4@cornell.edu> wrote:
> >
> > So Bob, you have said you don't care about speed, which is your choice,
> obviously. But for me this code is intolerably slow. Preview is useless
> even after I remove the chamfering and intersection to make it have
> cylindrical edges. And render takes 20s with manifold. Because the
> original code was unpreviewable I couldn't easily assess how well my
> rewrite matched, but it previews instantly and renders in 0.1s. (Note: a
> reason I care about preview is that I can color things that I overlay to
> see for example if two things match.)
> >
> > Another few things. In BOSL2, global variables that start with
> underscore are reserved for BOSL2 internal use, so you shouldn't be using
> those. You could clobber an internal definition. (Not sure why anyone
> would use variables that start with underscore as a choice---I find them
> very annoying.)
> >
> > The second is that I think your code measures tooth angle relative to
> the vertical instead of relative to the tooth ridge. This is not the
> normal way that tooth angle would be measured, e.g. on a gear. It means
> that actual angle is never what you specify.
> >
> > A third observation is that you should be chamfering the valleys just
> like the peaks. Internal corners are stress concentration points on an
> object and will weaken it. So my version can apply varying chamfers in
> both places.
> >
> > I personally find the rewritten code simpler than the original, as well
> as much faster, and there's probably room to clean it up more. (Could
> probably compute inner shape from outer with a scale() computation for
> example.) It does produce a polygonal result and could be intersected
> with a tube like the original to fix that if you think it's necessary. I
> imagine that one intersection wouldn't be a major drag on the speed. I
> agree that trying to compute the profile on a circular arc would be a pain.
> >
> > include <BOSL2/std.scad>
> >
> > // Number of Teeth
> > _n = 36; // Number Of Teeth
> >
> > // Inner Radius
> > _ir = 30;
> > // Outer Radius
> > _or = 50;
> > // Is the coupling conical?
> > _conic = 15;
> > // Tooth Profile Angle
> > _profile = 90; // [60, 90]
> > // Percentage of tooth height
> > _chamfer = 5; // Default 5%
> > _base = 1;
> >
> > function basic_profile(angle,chamfer_top, chamfer_bot) =
> > let(
> > width = tan(angle/2),
> > pts = [
> > [0,(-1+chamfer_bot)*width,chamfer_bot],
> > [0,-chamfer_top*width,1-chamfer_top]
> > ],
> > )
> > concat(pts, reverse(yflip(pts)));
> >
> > profwidth = tan(_profile/2);
> > outside = _or*tan(180/_n);
> > inside = _ir*tan(180/_n);
> >
> > prof_out = right(_or,scale(outside/profwidth,basic_profile(_profile,
> _chamfer/100, _chamfer/200)));
> > prof_in = right(_ir,scale(inside/profwidth,basic_profile(_profile,
> _chamfer/100, _chamfer/200)));
> >
> > offset = (_or-_ir) * tan(_conic);
> >
> > outfull = up(offset,[for(i=lerpn(0,360,_n,endpoint=false))
> > each zrot(i,prof_out)]);
> > infull = [for(i=lerpn(0,360,_n,endpoint=false))
> > each zrot(i,prof_in)];
> >
> > inbot = [for(val=infull) [val.x,val.y,-_base]];
> > outbot = [for(val=outfull) [val.x,val.y,-_base]];
> >
> > vnf_polyhedron(vnf_vertex_array([outfull, infull, inbot, outbot],
> reverse=true, col_wrap=true, row_wrap=true));
> >
> > <image.png>
> >
> >
> >
> >
> >
>
>

M
mikeonenine@web.de
Thu, Oct 31, 2024 4:02 AM
I think the tooth angle should be defined relative to the top line
of the teeth (ridge line?), but your code defines it relative to
absolute vertical, so as you change the conical angle the tooth angle
changes. And if the conical angle is zero the tooth angle is not the
specified
angle. At least that appeared to be the case with the version you
posted.
On Wed, Oct 30, 2024 at 9:52 PM Bob Carlson bob@rjcarlson.com wrote:
There are 3 angles I calculate. Tooth Angle is the angle between teeth
radially. It’s simple, 360/N. The other two are the groove angle and ridge
angle. These are calculated relative to horizontal. In a flat hirth joint,
they are plus and minus the same number. In a conical joint, it’s
different, but
Translating a polygon section of a spline up or down in the z-direction to get a conical Hirth joint would seem to save a lot of trouble. The ridge and groove angles stay the same, the spline width remains 360/n and the diameter doesn’t change, so the intersection is “straight” and you are only cutting off the apices of the polygon and not other bits and you know what you will get.
Adrian Mariano wrote:
> I think the tooth angle *should* be defined relative to the top line
> of the teeth (ridge line?), but your code defines it relative to
> absolute vertical, so as you change the conical angle the tooth angle
> changes. And if the conical angle is zero the tooth angle is not the
> specified
> angle. At least that appeared to be the case with the version you
> posted.
>
> On Wed, Oct 30, 2024 at 9:52 PM Bob Carlson [bob@rjcarlson.com](mailto:bob@rjcarlson.com) wrote:
>
> > There are 3 angles I calculate. Tooth Angle is the angle between teeth
> > radially. It’s simple, 360/N. The other two are the groove angle and ridge
> > angle. These are calculated relative to horizontal. In a flat hirth joint,
> > they are plus and minus the same number. In a conical joint, it’s
> > different, but
Translating a polygon section of a spline up or down in the z-direction to get a conical Hirth joint would seem to save a lot of trouble. The ridge and groove angles stay the same, the spline width remains 360/n and the diameter doesn’t change, so the intersection is “straight” and you are only cutting off the apices of the polygon and not other bits and you know what you will get.

JB
Jordan Brown
Thu, Oct 31, 2024 4:57 AM
On 10/30/2024 6:33 PM, Bob Carlson wrote:
On Oct 26, 2024, at 16:21, Jordan Brown
openscad@jordan.maileater.net wrote:
Also, a tidbit: _chamferF() generates a conical figure that might as
well be a cone.
up(_conic + _chamferHeight) scale(1.5) zcyl(h = _toothHeight/2 + _conic, r1 = _or, r2 = 0, anchor=TOP);
Since it's anchored at the top, I didn't have to fiddle with making
sure that it was slightly larger than the thing it's cutting from and
could just scale it up a bit.
When I tried switching to a cone rather than rotate_extrude, the
rendering time went up by about 50% (roughly a quarter second to .4
seconds). So, I’ve kept the current code.
My gut reaction was that they should be almost identical, but then I
realized that I don't know how rotate_extrude decides how many sides to
put on an object. Without looking at the sources, it looks like it
probably looks at the maximum X value to determine the radius and then
uses $fa/$fs/$fn as usual. I would look at how many sides each is
ending up with, and why.
But a rotate_extrude of a triangle with one side on the Y axis produces
a cone, and if you put the top point of the triangle at [0,0] then
you'll get the same effect I wanted - scaling it up leaves the top part
all the same.
On 10/30/2024 6:33 PM, Bob Carlson wrote:
>
>> On Oct 26, 2024, at 16:21, Jordan Brown
>> <openscad@jordan.maileater.net> wrote:
>>
>> Also, a tidbit: _chamferF() generates a conical figure that might as
>> well be a cone.
>> up(_conic + _chamferHeight) scale(1.5) zcyl(h = _toothHeight/2 + _conic, r1 = _or, r2 = 0, anchor=TOP);
>> Since it's anchored at the top, I didn't have to fiddle with making
>> sure that it was slightly larger than the thing it's cutting from and
>> could just scale it up a bit.
>
> When I tried switching to a cone rather than rotate_extrude, the
> rendering time went up by about 50% (roughly a quarter second to .4
> seconds). So, I’ve kept the current code.
>
My gut reaction was that they should be almost identical, but then I
realized that I don't know how rotate_extrude decides how many sides to
put on an object. Without looking at the sources, it looks like it
probably looks at the maximum X value to determine the radius and then
uses $fa/$fs/$fn as usual. I would look at how many sides each is
ending up with, and why.
But a rotate_extrude of a triangle with one side on the Y axis produces
a cone, and if you put the top point of the triangle at [0,0] then
you'll get the same effect I wanted - scaling it up leaves the top part
all the same.

M
mikeonenine@web.de
Thu, Oct 31, 2024 5:32 AM
On 10/30/2024 6:33 PM, Bob Carlson wrote:
On Oct 26, 2024, at 16:21, Jordan Brown
openscad@jordan.maileater.net wrote:
Also, a tidbit: _chamferF() generates a conical figure that might as
well be a cone.
up(_conic + _chamferHeight) scale(1.5) zcyl(h = _toothHeight/2 + _conic, r1 = _or, r2 = 0, anchor=TOP);
Since it's anchored at the top, I didn't have to fiddle with making
sure that it was slightly larger than the thing it's cutting from and
could just scale it up a bit.
When I tried switching to a cone rather than rotate_extrude, the
rendering time went up by about 50% (roughly a quarter second to .4
seconds). So, I’ve kept the current code.
My gut reaction was that they should be almost identical, but then I
realized that I don't know how rotate_extrude decides how many sides to
put on an object. Without looking at the sources, it looks like it
probably looks at the maximum X value to determine the radius and then
uses $fa/$fs/$fn as usual. I would look at how many sides each is
ending up with, and why.
But a rotate_extrude of a triangle with one side on the Y axis produces
a cone, and if you put the top point of the triangle at [0,0] then
you'll get the same effect I wanted - scaling it up leaves the top part
all the same.
An anticone needs rotate_extrude?
$fn=100;
//Cone:
translate([-110, 0, 0])
rotate_extrude()
polygon([
[60, 0],
[60, 10],
[100, 0],
[100, 0],
]);
//Anticone:
translate([110, 0, 0])
rotate_extrude()
polygon([
[60, 0],
[60, 0],
[100, 10],
[100, 0],
]);
Jordan Brown wrote:
> On 10/30/2024 6:33 PM, Bob Carlson wrote:
>
> > > On Oct 26, 2024, at 16:21, Jordan Brown
> > > [openscad@jordan.maileater.net](mailto:openscad@jordan.maileater.net) wrote:
> > >
> > > Also, a tidbit: _chamferF() generates a conical figure that might as
> > > well be a cone.
> > > up(_conic + _chamferHeight) scale(1.5) zcyl(h = _toothHeight/2 + _conic, r1 = _or, r2 = 0, anchor=TOP);
> > > Since it's anchored at the top, I didn't have to fiddle with making
> > > sure that it was slightly larger than the thing it's cutting from and
> > > could just scale it up a bit.
> >
> > When I tried switching to a cone rather than rotate_extrude, the
> > rendering time went up by about 50% (roughly a quarter second to .4
> > seconds). So, I’ve kept the current code.
>
> My gut reaction was that they should be almost identical, but then I
> realized that I don't know how rotate_extrude decides how many sides to
> put on an object. Without looking at the sources, it looks like it
> probably looks at the maximum X value to determine the radius and then
> uses $fa/$fs/$fn as usual. I would look at how many sides each is
> ending up with, and why.
>
> But a rotate_extrude of a triangle with one side on the Y axis produces
> a cone, and if you put the top point of the triangle at \[0,0\] then
> you'll get the same effect I wanted - scaling it up leaves the top part
> all the same.
An anticone needs rotate_extrude?
`$fn=100;`
`//Cone:`
`translate([-110, 0, 0])`
`rotate_extrude()`
`polygon([`
`[60, 0],`
`[60, 10],`
`[100, 0],`
`[100, 0],`
`]);`
`//Anticone:`
`translate([110, 0, 0])`
`rotate_extrude()`
`polygon([`
`[60, 0],`
`[60, 0],`
`[100, 10],`
`[100, 0],`
`]);`


JB
Jordan Brown
Thu, Oct 31, 2024 6:58 AM
On 10/30/2024 10:32 PM, Caddiy via Discuss wrote:
An anticone needs rotate_extrude?
I wouldn't call either of those shapes cones; I would call the first a
cylinder from which a point-down cone has been subtracted, and the
second a point-up cone from which a cylinder has been subtracted.
You could build either of them with rotate_extrude(), as you have, or
you could build them as the differences above. Which is "best" probably
depends on whether what you have convenient is the coordinates of the
inner edge, or the coordinates of the point of the cone.
I'd give you difference-between-cone-and-cylinder examples, but I don't
have the coordinates of the point of the cone handy. I'd have to
extrapolate from the upper side of the triangles. That's not hard, but
it's midnight and I don't wanna :-)
On 10/30/2024 10:32 PM, Caddiy via Discuss wrote:
>
> An anticone needs rotate_extrude?
>
I wouldn't call either of those shapes cones; I would call the first a
cylinder from which a point-down cone has been subtracted, and the
second a point-up cone from which a cylinder has been subtracted.
You could build either of them with rotate_extrude(), as you have, or
you could build them as the differences above. Which is "best" probably
depends on whether what you have convenient is the coordinates of the
inner edge, or the coordinates of the point of the cone.
I'd give you difference-between-cone-and-cylinder examples, but I don't
have the coordinates of the point of the cone handy. I'd have to
extrapolate from the upper side of the triangles. That's not hard, but
it's midnight and I don't wanna :-)




