Multmatrix can be used to map an object to a new location/rotation

you can use this template to create the 4x4 matrix

X    Y    Z  P
X    Y    Z  P
X    Y    Z  P
0    0      0  1

X: direction of new x axis with size 1
Y : direction of new y axis with size 1
Z: direction od new z axis with size 1

P : positional offset

so your matrix is a z rotation with some offset

hope that helps

On Fri, Nov 22, 2024 at 5:23 AM Leonard Martin Struttmann via Discuss <
discuss@lists.openscad.org> wrote:

On 11/21/2024 8:23 PM, Leonard Martin Struttmann via Discuss wrote:

Some people can directly think in terms of matrix transformations.  I'm
not one of them.

Shearing is when a change in one axis causes a linear change in another
axis.

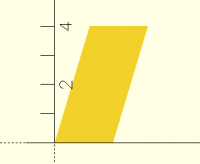
Looking at it two-dimensionally, this is a square that has been
sheared.  (I'm not clear on whether it's sheared X along Y, or vice
versa.)  The key thing is that for every unit of +Y, X has been shifted.

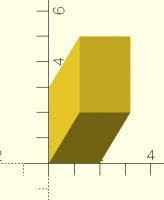
Now, actually, that's a face-on view of a cube that's been sheared in
two axes, but that's harder to see in a single 2D image:

Here, for every unit of +Z, X and Y have been shifted +1.

That's the format of the matrix for a scaling operation. 
Transformation matrixes are used for every transformation operation that
OpenSCAD does - translate, rotate, scale, mirror.  (Did I miss any?) 
It's all a question of what you put in each cell.

I'll try.  Simple transformation matrixes are relatively
understandable.  Here's the program that generated that cube:

module shearXY(xy) {
    m = [
        [1, 0, xy.x],
        [0, 1, xy.y],
        [0, 0, 1],
    ];
    multmatrix(m) children();
}

shearXY([1,1]) cube(10);

This is the combination of the identity matrix (1s all along the
diagonal) and shear factors along the third column.  The first shear
factor says how much X will change for each unit of Z change, and the
second says how much Y will change for every unit of Z change.

Now, why does that work?

Back to your high school math - Algebra 2, if I recall correctly. 
Matrix multiplication.

Let's use a more interesting example, so that the numbers are all different:

shearXY([0.3,0.5]) cube([2,3,4]);

Take the coordinate - say, the [1,2,3] of the "outside" corner of the
cube.  Lay it out above the matrix:

 2    3   4

 1    0   0.3
 0    1   0.5
 0    0   1

Multiply the number from the coordinate by each of the numbers below it.

 2    0   1.2
 0    3   2
 0    0   4

Now add across:

 2    0   1.2  =  3.2
 0    3   2    =  5
 0    0   4    =  4

That, [3.2, 5, 4], is the transformed coordinate.

Another way to look at it is:

newX = X + 0.3*Z
newY = Y + 0.5*Z
newZ = Z

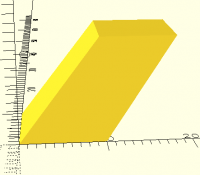
Sanity check... here's a top-down view of that figure:

Again, we're looking at the topmost, rightmost, backmost point on the
cube.  X... yeah, that looks like 3.2.  Y... yeah, looks like 5.  For Z
we need one of the side views; here's the front view:

Yep, Z is 4.

Again, for this shear we have said - the parameter to shearXY - that for
each unit of +Z, we want to change X by +0.3 and Y by +0.5.

Each transformation has its own unique "pattern" for a transformation
matrix.  I've given you a shear matrix, what I suspect is called "shear
X and Y along Z".  To shear along the other axes - for instance, so that
Y and Z are modified as you change X - move those shear factors over
into the one of the other columns.

A scale matrix is simple:

[
    [ sx,  0,  0 ],
    [  0, sy,  0 ],
    [  0,  0, sz ],
]

And note that if the scale factors are all 1, what you have is the
1-along-the-diagonal of an identity matrix.

Rotation matrixes require trig, and frankly I usually just look them up.

https://en.wikipedia.org/wiki/Rotation_matrix#Basic_3D_rotations

The example that you give, with the sines and cosines, is a rotation
matrix (plus more, which I'll explain in a moment).

Translation requires a bit more trickery, because it requires moving in
one or more axis no matter what the values are.  For that, we add a
"1" to the end of the original coordinate, and we put the translation
into a fourth column of the matrix.  Let's translate [2,3,4] to the +X
by 5 and to the +Y by 6, and do the same multiply-and-add process:

2  3  4  1

1  0  0  5   = 7
0  1  0  6   = 9
0  0  1  0   = 4

and do the same multiply-and-add process. Note that the left 3 columns
leave the coordinate unchanged, and then the right column (which gets
multiplied by 1) does the actual translation.

So why do we do this?  Because matrix arithmetic is arithmetic, and you
can chain operations together.  If you want to scale and then translate,
you could take your original point and multiply it by a scale matrix and
then multiply it by a translate matrix... or you could multiply the
scale matrix by the translate matrix to get a matrix that does both,
and then you do one matrix multiply of your coordinate by the combined
matrix to get the result.  That's how OpenSCAD, and virtually all
graphics software, does things like rotation, translation, scaling, et
cetera of these objects - including when you move the camera around -
and does it relatively fast.

Mostly, you don't need to derive your own matrixes.  Just go look them
up.  BOSL2 has functions that generate most of them.  And then you
multiply them together in the combination that you want.

Hope that helps.

On 2024-11-22 05:23, Leonard Martin Struttmann via Discuss wrote:

Look up the terms 'homogenous coordinates' and 'homogenous
transformation matrices'. Then also make sure you understand how
matrix/vector multiplication works.

Ordinary cartesian 3d coordinates can be written as vectors
x
y
z

Homogenous coordinates are the same, but with a fourth component,
usually set to 1
x
y
z
1

Since homogenous transformation matrices are 4x4 matrices they can (via
multiplication with homogenous coordinates) express all common
transformations, including rotations, scaling, translations and
mirroring. Also less common transformation like shearing is possible.

Carsten Arnholm

If you export as csg, then it replaces the transformations with
multimatrix. Instead of 'union()', it uses  'group()' . If you write
openscad script you can use 'group' instead of 'union'. Are there other
duplicated names? I don't think 'group' is mentioned in the openscad
documentation.

On 22/11/2024 08:33, Carsten Arnholm via Discuss wrote:

Yes, the group commandis really strange, I have not seen it in the
documentation, just in the source code and
I am not even sure if it actually unions the objects but only puts all
triangles into one bucket.
Maybe group() is needed to stay backward- compatible with other tools ?

On Fri, Nov 22, 2024 at 11:43 AM Raymond West via Discuss <
discuss@lists.openscad.org> wrote:



As best I can tell, group() is identical to union().  Its comments say that it doesn’t union its children, but GeometryEvaluator::visit(GroupNode) just calls GeometryEvaluator::visit(AbstractNode), and that calls applyToChildren(OpenSCADOperator::UNION) just like union() does.  I think the intent might have been to allow for returning un-unioned collections of shapes that might be unioned by a parent or might not, but I don’t think it ever happened.  Interestingly, ListNode seems to have the same goal, but tied into lazy union.

Ok, that's a lot to chew on.  Since I, like Jordan, am not someone that
"gets" matrix operations, this will take me a while to digest.

Thanks, everyone, for such complete and extensive explanations.  I really
appreciate it.

Len

On Fri, Nov 22, 2024 at 9:39 AM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:

Thanks for the tip on homogeneous coordinates and matrices.

As I understand it both a scale and a translate involve matrix multiplication, so is a multmatrix with appropriate coordinates more efficient  than a translate and a scale? It would seem that that’s only one matrix multiplication rather than two.

It seems that multmatrix only works in 3D, so is a multmatrix still more efficient than a 2D translate and scale?

Mark

Yes it is normal to multiply all the transformation matrices together and
then use the result to pass to multimatrix.

You could do the same in 2D with 3x3 matrices.

On Fri, 22 Nov 2024 at 17:37, Mark Erbaugh via Discuss <
discuss@lists.openscad.org> wrote: