multmatrix()
On 11/22/2024 9:37 AM, Mark Erbaugh via Discuss wrote:
As I understand it both a scale and a translate involve matrix
multiplication, so is a multmatrix with appropriate coordinates more
efficient than a translate and a scale? It would seem that that’s
only one matrix multiplication rather than two.
Any difference is lost in the noise. The actual point-by-point work is
done by first multiplying together all of the stacked transformation
matrixes, and then multiplying the points by that composite matrix.
Adding a transformation adds one matrix multiply... not one per point,
one. There's a microscopic cost to that, but it's probably smaller
than the cost of parsing the statements - and a multmatrix with a
constant matrix is more expensive to parse than an individual
transformation. (But that cost is microscopic too.)
It seems that multmatrix only works in 3D, [...]
Why do you say that?
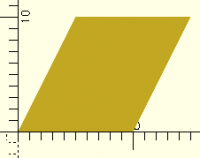
multmatrix([
[ 1, 0.5 ],
[ 0, 1 ],
]) square(10);
When should you use multmatrix?
- When you have a transformation matrix supplied to use, e.g. as a
result of some of BOSL2's functions. - When you need to do something that the "ordinary" transformation
operators can't do, like skew.
Other than those - and even there, write skew once and call it - use the
ordinary operators. There's no performance penalty, it's a lot easier,
and it's a lot easier to read.
On 2024-11-22 18:37, Mark Erbaugh via Discuss wrote:
Thanks for the tip on homogeneous coordinates and matrices.
As I understand it both a scale and a translate involve matrix
multiplication, so is a multmatrix with appropriate coordinates more
efficient than a translate and a scale? It would seem that that’s
only one matrix multiplication rather than two.
It seems that multmatrix only works in 3D, so is a multmatrix still
more efficient than a 2D translate and scale?
scale() and translate() are just 'syntactic sugar', they create 4x4
homogenous transformation matrices with appropriate values in the right
places without showing you the details. When you apply multiple such
transformations, their matrices are multiplied together to create a
final transformation matrix encapsulating the total. If you wanted to
you could do the same by applying a succession of multmatrix()
operations.
To be clear, any basic transformation can be expressed as a 4x4 matrix.
Multiplying such matrices with each other (in the right order, matrix
multiplication is not commutative) yields a 4x4 matrix expressing them
all.
Homogenuous transformation works in 2d or 3d. If you keep one dimension
(e.g. z) unchanged (as compared to identity matrix) you can perform 2d
transformations just fine.
Thank you for the explanation. That makes sense and my test using the render time (the multmatrix was only part of the model) at the end did show no real difference.
The reason I say only 3D operation is that when I created a 3 by 3 matrix with the translate vector in the third column, the translate didn’t work. I had to put it in the fourth column. As I read the multmatrix documentation, it pads with zeros (Except for the bottom right, which is a 1 to get a 4 by 4).
Internally, are all OpenSCAD operations done with 3D matrix multiplication, even when dealing with 2D objects?
Mark
On Nov 22, 2024, at 10:45 AM, Leonard Martin Struttmann via Discuss discuss@lists.openscad.org wrote:
Ok, that's a lot to chew on. Since I, like Jordan, am not someone that "gets" matrix operations, this will take me a while to digest.
Thanks, everyone, for such complete and extensive explanations. I really appreciate it.
Len
On Fri, Nov 22, 2024 at 9:39 AM Jordan Brown via Discuss <discuss@lists.openscad.org mailto:discuss@lists.openscad.org> wrote:
Yes, the group commandis really strange, I have not seen it in the documentation, just in the source code and I am not even sure if it actually unions the objects but only puts all triangles into one bucket.
Maybe group() is needed to stay backward- compatible with other tools ?
As best I can tell, group() is identical to union(). Its comments say that it doesn’t union its children, but GeometryEvaluator::visit(GroupNode) just calls GeometryEvaluator::visit(AbstractNode), and that calls applyToChildren(OpenSCADOperator::UNION) just like union() does. I think the intent might have been to allow for returning un-unioned collections of shapes that might be unioned by a parent or might not, but I don’t think it ever happened. Interestingly, ListNode seems to have the same goal, but tied into lazy union.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org mailto:discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On 11/22/2024 10:13 AM, Mark Erbaugh via Discuss wrote:
Internally, are all OpenSCAD operations done with 3D matrix
multiplication, even when dealing with 2D objects?
Yes. (Confirmed by source inspection.) Note that you can move 2D
objects off of the XY plane, though their behavior at that point is ...
interesting.
Here's a shear module, seems to be OK.
module shear(v) {
// Check if the input vector is 2D or 3D
is_2d = len(v) == 2;
if (is_2d) {
// 2D Shear Transformation
shear_matrix = [
[1, tan(v[0]), 0],
[tan(v[1]), 1, 0],
[0, 0, 1]
];
multmatrix(shear_matrix)
children();
}
else {
// 3D Shear Transformation
shear_matrix = [
[1, tan(v[0]), tan(v[2]), 0],
[0, 1, tan(v[2]), 0],
[0,0,1,0],
[0, 0, 0, 1]
];
multmatrix(shear_matrix)
children();
}
}
// 2D Shear
shear([40,30]) {
translate([0,0,10])
square([5, 20]);
}
// 3D Shear
shear([130,20,10]) {
cube(10,true);
}
On 22/11/2024 21:59, Jordan Brown via Discuss wrote:
On 11/22/2024 10:13 AM, Mark Erbaugh via Discuss wrote:
Internally, are all OpenSCAD operations done with 3D matrix
multiplication, even when dealing with 2D objects?
Yes. (Confirmed by source inspection.) Note that you can move 2D
objects off of the XY plane, though their behavior at that point is
... interesting.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On 11/23/2024 2:55 AM, Raymond West via Discuss wrote:
Here's a shear module, seems to be OK.
I haven't thought of shears as angles, though I suppose there's no
reason why not.
// 3D Shear Transformation
shear_matrix = [
[1, tan(v[0]), tan(v[2]), 0],
[0, 1, tan(v[2]), 0],
[0,0,1,0],
[0, 0, 0, 1]
];
You don't use v[1], and you use v[2] twice.
But also note that in a 3x3 transformation matrix, there are six
non-diagonal values:
- a b
c - d
e f -
Those six values control shear, and each of them does a different shear.
a
Increasing Y increases X
b
Increasing Z increases X
c
Increasing X increases Y
d
Increasing Z increases Y
e
Increasing X increases Z
f
Increasing Y increases Z
Note that for each axis, it can control the other two axes and can be
controlled by the other two axes.
(To complete the picture: the diagonal values are X-increases-X,
Y-increases-Y, and Z-increases-Z, and we usually think of those as scale.)
You don't have any way to control c, e, or f, which means that you can't
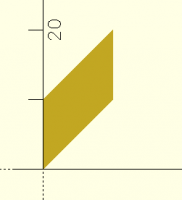
do this 3D shear (front view, orthogonal) controlled by e:
In particular, the [1,0,0] along the first column means that X never
changes Y or Z - the front bottom edge of the cube will never change -
and the 0 in the third row, second column means that Y never changes Z.
It seems like a fully-general 3D shear function would need to take all
six values as parameters. Also, given that I thought of shearing in
terms of ratios (e.g., for every unit of +X, shift Z by 2) and you
thought of it in terms of angles, it seems like both angles and ratios
should be supported.
And as I started to think about what the arguments might be, I said "I
bet that BOSL2 has already done this". And indeed it has.
https://github.com/BelfrySCAD/BOSL2/wiki/Tutorial-Transforms#skewing
https://github.com/BelfrySCAD/BOSL2/wiki/transforms.scad#functionmodule-skew
It allows you to specify all six values as either ratios or angles.
Thanks, typo corrected
// 3D Shear Transformation
shear_matrix = [
[1, tan(v[0]), tan(v[1]), 0],
[0, 1, tan(v[2]), 0],
[0,0,1,0],
[0, 0, 0, 1]
];
As you mention, this is a subset of the full shear options. Perhaps I
should rename the module to 'lean'.
On 23/11/2024 18:49, Jordan Brown wrote:
On 11/23/2024 2:55 AM, Raymond West via Discuss wrote:
Here's a shear module, seems to be OK.
I haven't thought of shears as angles, though I suppose there's no
reason why not.
// 3D Shear Transformation
shear_matrix = [
[1, tan(v[0]), tan(v[2]), 0],
[0, 1, tan(v[2]), 0],
[0,0,1,0],
[0, 0, 0, 1]
];
You don't use v[1], and you use v[2] twice.
But also note that in a 3x3 transformation matrix, there are six
non-diagonal values:
- a b
c - d
e f -
Those six values control shear, and each of them does a different shear.
a
Increasing Y increases X
b
Increasing Z increases X
c
Increasing X increases Y
d
Increasing Z increases Y
e
Increasing X increases Z
f
Increasing Y increases Z
Note that for each axis, it can control the other two axes and can be
controlled by the other two axes.
(To complete the picture: the diagonal values are X-increases-X,
Y-increases-Y, and Z-increases-Z, and we usually think of those as scale.)
You don't have any way to control c, e, or f, which means that you
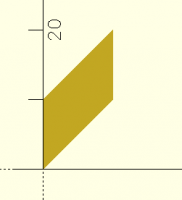
can't do this 3D shear (front view, orthogonal) controlled by e:
In particular, the [1,0,0] along the first column means that X never
changes Y or Z - the front bottom edge of the cube will never change -
and the 0 in the third row, second column means that Y never changes Z.
It seems like a fully-general 3D shear function would need to take all
six values as parameters. Also, given that I thought of shearing in
terms of ratios (e.g., for every unit of +X, shift Z by 2) and you
thought of it in terms of angles, it seems like both angles and ratios
should be supported.
And as I started to think about what the arguments might be, I said "I
bet that BOSL2 has already done this". And indeed it has.
https://github.com/BelfrySCAD/BOSL2/wiki/Tutorial-Transforms#skewing
https://github.com/BelfrySCAD/BOSL2/wiki/transforms.scad#functionmodule-skew
It allows you to specify all six values as either ratios or angles.