JW
Joe Weinpert
Fri, Oct 31, 2025 6:29 PM
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
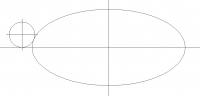
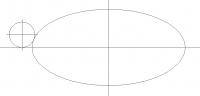
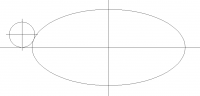
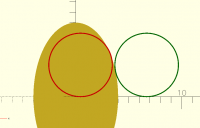
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
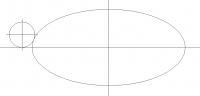
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art <http://jwstudio.art>

DP
Dan Perry
Fri, Oct 31, 2025 7:31 PM
In the following equations, a is the ellipse radius in x direction, b is
the ellipse radius in y direction (or it's the other way around 😊). I'm
pretty sure for your case, you just need to increase the radius of your
ellipse by 1 in x and y.
function ellipse_y_from_known_x(a, b, x) = bsqrt(1 - x^2/a^2);
function ellipse_x_from_known_y(a, b, y) = asqrt(1 - y^2/b^2);
Dan
On Fri, Oct 31, 2025 at 6:30 PM Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
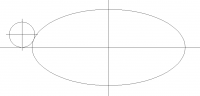
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
In the following equations, a is the ellipse radius in x direction, b is
the ellipse radius in y direction (or it's the other way around 😊). I'm
pretty sure for your case, you just need to increase the radius of your
ellipse by 1 in x and y.
function ellipse_y_from_known_x(a, b, x) = b*sqrt(1 - x^2/a^2);
function ellipse_x_from_known_y(a, b, y) = a*sqrt(1 - y^2/b^2);
Dan
On Fri, Oct 31, 2025 at 6:30 PM Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
> To all the math wizards out here:
>
> I need a formula(?) or steps involved in finding the XY centerpoint of a
> radius to be tangent to an ellipse.
>
> Attached pic:
>
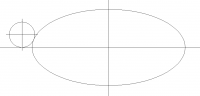
> ellipse size x = 20, y = 9
> ellipse centerpoint x = 12, y = 6
> fillet dia = 2
> fillet centerpoint x = ?, y = 1
>
> I need to determine where x of the centerpoint will be for the fillet.
>
>
> [image: image.png]
>
>
> Joe Weinpert
> joe.weinpert@gmail.com
> www.jwstudio.art <http://jwstudio.art>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

NS
Nathan Sokalski
Fri, Oct 31, 2025 7:35 PM
It's been a long time since I took calculus, but here are some steps that may help:
A derivative, the main topic of calculus, determines the slope of y=f(x)
So your main steps would be to define both your ellipses as a y=f(x) equation, solve for the derivative, and then solve for where they are equal. This is probably not the clearest most detailed explanation, but one thing that I have recently started using a lot for my OpenSCAD geometry is AI. It gives very good explanations, and you can ask & re-ask the questions as many times as you want, so nobody will get annoyed with you for being a pain in the butt, and you don't need to feel embarrassed about asking little stuff along the way. It will even write some of your code for you if you ask, so it will majorly speed up some of the work that you used to make (what feels like) stupid makes missing little mistakes.
Nathan Sokalski
njsokalski@hotmail.commailto:njsokalski@hotmail.com
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image.png]
Joe Weinpert
joe.weinpert@gmail.commailto:joe.weinpert@gmail.com
www.jwstudio.arthttp://jwstudio.art
It's been a long time since I took calculus, but here are some steps that may help:
A derivative, the main topic of calculus, determines the slope of y=f(x)
So your main steps would be to define both your ellipses as a y=f(x) equation, solve for the derivative, and then solve for where they are equal. This is probably not the clearest most detailed explanation, but one thing that I have recently started using a lot for my OpenSCAD geometry is AI. It gives very good explanations, and you can ask & re-ask the questions as many times as you want, so nobody will get annoyed with you for being a pain in the butt, and you don't need to feel embarrassed about asking little stuff along the way. It will even write some of your code for you if you ask, so it will majorly speed up some of the work that you used to make (what feels like) stupid makes missing little mistakes.
Nathan Sokalski
njsokalski@hotmail.com<mailto:njsokalski@hotmail.com>
________________________________
From: Joe Weinpert via Discuss <discuss@lists.openscad.org>
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion <discuss@lists.openscad.org>
Cc: Joe Weinpert <joe.weinpert@gmail.com>
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image.png]
Joe Weinpert
joe.weinpert@gmail.com<mailto:joe.weinpert@gmail.com>
www.jwstudio.art<http://jwstudio.art>

AM
Adrian Mariano
Fri, Oct 31, 2025 8:40 PM
Below is the solution. I approached the problem like this. Given ellipse
with axes a, b, and desired radius r, suppose y<a. Find the corresponding
point x so that (x,y) is on the ellipse (in quadrant 1). The gradient of
the ellipse equation is n = 2(x/a^2,y/b^2). The center of a circle that is
tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The desired circle
is also tangent to the x axis, which means the y component of its center
equals r. That gives you an equation in x and y. The x can be eliminated
using the ellipse equation. Rearrange the terms and you have a quartic
(degree 4) polynomial. Solve that, pick the correct root, and you're
done. I wouldn't call this a simple problem, and finding a strategy that
constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2rk, b^4+r^2k-r^2a^2, -2rb^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
It's been a long time since I took calculus, but here are some steps that
may help:
A derivative, the main topic of calculus, determines the slope of y=f(x)
So your main steps would be to define both your ellipses as a y=f(x)
equation, solve for the derivative, and then solve for where they are
equal. This is probably not the clearest most detailed explanation, but one
thing that I have recently started using a lot for my OpenSCAD geometry is
AI. It gives very good explanations, and you can ask & re-ask the questions
as many times as you want, so nobody will get annoyed with you for being a
pain in the butt, and you don't need to feel embarrassed about asking
little stuff along the way. It will even write some of your code for you if
you ask, so it will majorly speed up some of the work that you used to make
(what feels like) stupid makes missing little mistakes.
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Below is the solution. I approached the problem like this. Given ellipse
with axes a, b, and desired radius r, suppose y<a. Find the corresponding
point x so that (x,y) is on the ellipse (in quadrant 1). The gradient of
the ellipse equation is n = 2(x/a^2,y/b^2). The center of a circle that is
tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The desired circle
is also tangent to the x axis, which means the y component of its center
equals r. That gives you an equation in x and y. The x can be eliminated
using the ellipse equation. Rearrange the terms and you have a quartic
(degree 4) polynomial. Solve that, pick the correct root, and you're
done. I wouldn't call this a simple problem, and finding a strategy that
constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2*r*k, b^4+r^2*k-r^2*a^2, -2*r*b^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
> It's been a long time since I took calculus, but here are some steps that
> may help:
>
> A derivative, the main topic of calculus, determines the slope of y=f(x)
>
> So your main steps would be to define both your ellipses as a y=f(x)
> equation, solve for the derivative, and then solve for where they are
> equal. This is probably not the clearest most detailed explanation, but one
> thing that I have recently started using a lot for my OpenSCAD geometry is
> AI. It gives very good explanations, and you can ask & re-ask the questions
> as many times as you want, so nobody will get annoyed with you for being a
> pain in the butt, and you don't need to feel embarrassed about asking
> little stuff along the way. It will even write some of your code for you if
> you ask, so it will majorly speed up some of the work that you used to make
> (what feels like) stupid makes missing little mistakes.
>
> Nathan Sokalski
> njsokalski@hotmail.com
> ------------------------------
> *From:* Joe Weinpert via Discuss <discuss@lists.openscad.org>
> *Sent:* Friday, October 31, 2025 2:29 PM
> *To:* OpenSCAD general discussion <discuss@lists.openscad.org>
> *Cc:* Joe Weinpert <joe.weinpert@gmail.com>
> *Subject:* [OpenSCAD] Need a geometry formula
>
> To all the math wizards out here:
>
> I need a formula(?) or steps involved in finding the XY centerpoint of a
> radius to be tangent to an ellipse.
>
> Attached pic:
>
> ellipse size x = 20, y = 9
> ellipse centerpoint x = 12, y = 6
> fillet dia = 2
> fillet centerpoint x = ?, y = 1
>
> I need to determine where x of the centerpoint will be for the fillet.
>
>
> [image: image.png]
>
>
> Joe Weinpert
> joe.weinpert@gmail.com
> www.jwstudio.art <http://jwstudio.art>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>

AM
Adrian Mariano
Fri, Oct 31, 2025 9:00 PM
Looks like it's a bit trickier than shown to select the right root. You
need to ignore negative roots as well, and even then I saw a weird case
where there were two solutions, but one was wrong. So you might need to
actually verify which solution is right if that happens. I don't know the
circumstances that create these various cases.
On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano avm4@cornell.edu wrote:
Below is the solution. I approached the problem like this. Given ellipse
with axes a, b, and desired radius r, suppose y<a. Find the corresponding
point x so that (x,y) is on the ellipse (in quadrant 1). The gradient of
the ellipse equation is n = 2(x/a^2,y/b^2). The center of a circle that is
tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The desired circle
is also tangent to the x axis, which means the y component of its center
equals r. That gives you an equation in x and y. The x can be eliminated
using the ellipse equation. Rearrange the terms and you have a quartic
(degree 4) polynomial. Solve that, pick the correct root, and you're
done. I wouldn't call this a simple problem, and finding a strategy that
constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2rk, b^4+r^2k-r^2a^2, -2rb^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
It's been a long time since I took calculus, but here are some steps that
may help:
A derivative, the main topic of calculus, determines the slope of y=f(x)
So your main steps would be to define both your ellipses as a y=f(x)
equation, solve for the derivative, and then solve for where they are
equal. This is probably not the clearest most detailed explanation, but one
thing that I have recently started using a lot for my OpenSCAD geometry is
AI. It gives very good explanations, and you can ask & re-ask the questions
as many times as you want, so nobody will get annoyed with you for being a
pain in the butt, and you don't need to feel embarrassed about asking
little stuff along the way. It will even write some of your code for you if
you ask, so it will majorly speed up some of the work that you used to make
(what feels like) stupid makes missing little mistakes.
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Looks like it's a bit trickier than shown to select the right root. You
need to ignore negative roots as well, and even then I saw a weird case
where there were two solutions, but one was wrong. So you might need to
actually verify which solution is right if that happens. I don't know the
circumstances that create these various cases.
On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano <avm4@cornell.edu> wrote:
> Below is the solution. I approached the problem like this. Given ellipse
> with axes a, b, and desired radius r, suppose y<a. Find the corresponding
> point x so that (x,y) is on the ellipse (in quadrant 1). The gradient of
> the ellipse equation is n = 2(x/a^2,y/b^2). The center of a circle that is
> tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The desired circle
> is also tangent to the x axis, which means the y component of its center
> equals r. That gives you an equation in x and y. The x can be eliminated
> using the ellipse equation. Rearrange the terms and you have a quartic
> (degree 4) polynomial. Solve that, pick the correct root, and you're
> done. I wouldn't call this a simple problem, and finding a strategy that
> constrains the messiness of the algebra requires some care.
>
> include<BOSL2/std.scad>
>
> $fn=120;
>
> a=10;
> b=4;
> r=3;
>
> function find_c(a,b,r,y) =
> let(
> x2 = a^2*(1-y^2/b^2),
> x = sqrt(x2),
> n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
> c = [x,y] + r*n
> )
> c;
>
> k = a^2-b^2;
> poly = [k, -2*r*k, b^4+r^2*k-r^2*a^2, -2*r*b^4, r^2*b^4];
>
> y=[for(p=real_roots(poly)) if (p<b) p];
>
> echo(y=y);
>
> if (len(y)==1){
> ellipse([a,b]);
> move(find_c(a,b,r,y[0]))
> circle(r=r);
> }
> else // This shouldn't happen
> echo("failed to find tangent point");
>
>
> On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> It's been a long time since I took calculus, but here are some steps that
>> may help:
>>
>> A derivative, the main topic of calculus, determines the slope of y=f(x)
>>
>> So your main steps would be to define both your ellipses as a y=f(x)
>> equation, solve for the derivative, and then solve for where they are
>> equal. This is probably not the clearest most detailed explanation, but one
>> thing that I have recently started using a lot for my OpenSCAD geometry is
>> AI. It gives very good explanations, and you can ask & re-ask the questions
>> as many times as you want, so nobody will get annoyed with you for being a
>> pain in the butt, and you don't need to feel embarrassed about asking
>> little stuff along the way. It will even write some of your code for you if
>> you ask, so it will majorly speed up some of the work that you used to make
>> (what feels like) stupid makes missing little mistakes.
>>
>> Nathan Sokalski
>> njsokalski@hotmail.com
>> ------------------------------
>> *From:* Joe Weinpert via Discuss <discuss@lists.openscad.org>
>> *Sent:* Friday, October 31, 2025 2:29 PM
>> *To:* OpenSCAD general discussion <discuss@lists.openscad.org>
>> *Cc:* Joe Weinpert <joe.weinpert@gmail.com>
>> *Subject:* [OpenSCAD] Need a geometry formula
>>
>> To all the math wizards out here:
>>
>> I need a formula(?) or steps involved in finding the XY centerpoint of a
>> radius to be tangent to an ellipse.
>>
>> Attached pic:
>>
>> ellipse size x = 20, y = 9
>> ellipse centerpoint x = 12, y = 6
>> fillet dia = 2
>> fillet centerpoint x = ?, y = 1
>>
>> I need to determine where x of the centerpoint will be for the fillet.
>>
>>
>> [image: image.png]
>>
>>
>> Joe Weinpert
>> joe.weinpert@gmail.com
>> www.jwstudio.art <http://jwstudio.art>
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
>

AM
Adrian Mariano
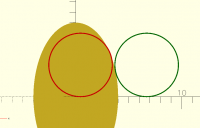
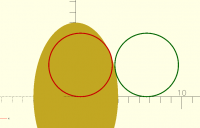
Fri, Oct 31, 2025 9:52 PM
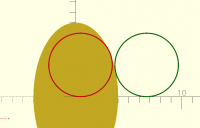
The wrong solution is a circle tangent on the inside of the ellipse. See
below.
[image: image.png]
On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano avm4@cornell.edu wrote:
Looks like it's a bit trickier than shown to select the right root. You
need to ignore negative roots as well, and even then I saw a weird case
where there were two solutions, but one was wrong. So you might need to
actually verify which solution is right if that happens. I don't know the
circumstances that create these various cases.
On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano avm4@cornell.edu wrote:
Below is the solution. I approached the problem like this. Given
ellipse with axes a, b, and desired radius r, suppose y<a. Find the
corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
desired circle is also tangent to the x axis, which means the y component
of its center equals r. That gives you an equation in x and y. The x can
be eliminated using the ellipse equation. Rearrange the terms and you have
a quartic (degree 4) polynomial. Solve that, pick the correct root, and
you're done. I wouldn't call this a simple problem, and finding a strategy
that constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2rk, b^4+r^2k-r^2a^2, -2rb^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
It's been a long time since I took calculus, but here are some steps
that may help:
A derivative, the main topic of calculus, determines the slope of y=f(x)
So your main steps would be to define both your ellipses as a y=f(x)
equation, solve for the derivative, and then solve for where they are
equal. This is probably not the clearest most detailed explanation, but one
thing that I have recently started using a lot for my OpenSCAD geometry is
AI. It gives very good explanations, and you can ask & re-ask the questions
as many times as you want, so nobody will get annoyed with you for being a
pain in the butt, and you don't need to feel embarrassed about asking
little stuff along the way. It will even write some of your code for you if
you ask, so it will majorly speed up some of the work that you used to make
(what feels like) stupid makes missing little mistakes.
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
The wrong solution is a circle tangent on the *inside* of the ellipse. See
below.
[image: image.png]
On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano <avm4@cornell.edu> wrote:
> Looks like it's a bit trickier than shown to select the right root. You
> need to ignore negative roots as well, and even then I saw a weird case
> where there were two solutions, but one was wrong. So you might need to
> actually verify which solution is right if that happens. I don't know the
> circumstances that create these various cases.
>
>
> On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Below is the solution. I approached the problem like this. Given
>> ellipse with axes a, b, and desired radius r, suppose y<a. Find the
>> corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
>> gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
>> circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
>> desired circle is also tangent to the x axis, which means the y component
>> of its center equals r. That gives you an equation in x and y. The x can
>> be eliminated using the ellipse equation. Rearrange the terms and you have
>> a quartic (degree 4) polynomial. Solve that, pick the correct root, and
>> you're done. I wouldn't call this a simple problem, and finding a strategy
>> that constrains the messiness of the algebra requires some care.
>>
>> include<BOSL2/std.scad>
>>
>> $fn=120;
>>
>> a=10;
>> b=4;
>> r=3;
>>
>> function find_c(a,b,r,y) =
>> let(
>> x2 = a^2*(1-y^2/b^2),
>> x = sqrt(x2),
>> n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
>> c = [x,y] + r*n
>> )
>> c;
>>
>> k = a^2-b^2;
>> poly = [k, -2*r*k, b^4+r^2*k-r^2*a^2, -2*r*b^4, r^2*b^4];
>>
>> y=[for(p=real_roots(poly)) if (p<b) p];
>>
>> echo(y=y);
>>
>> if (len(y)==1){
>> ellipse([a,b]);
>> move(find_c(a,b,r,y[0]))
>> circle(r=r);
>> }
>> else // This shouldn't happen
>> echo("failed to find tangent point");
>>
>>
>> On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>>> It's been a long time since I took calculus, but here are some steps
>>> that may help:
>>>
>>> A derivative, the main topic of calculus, determines the slope of y=f(x)
>>>
>>> So your main steps would be to define both your ellipses as a y=f(x)
>>> equation, solve for the derivative, and then solve for where they are
>>> equal. This is probably not the clearest most detailed explanation, but one
>>> thing that I have recently started using a lot for my OpenSCAD geometry is
>>> AI. It gives very good explanations, and you can ask & re-ask the questions
>>> as many times as you want, so nobody will get annoyed with you for being a
>>> pain in the butt, and you don't need to feel embarrassed about asking
>>> little stuff along the way. It will even write some of your code for you if
>>> you ask, so it will majorly speed up some of the work that you used to make
>>> (what feels like) stupid makes missing little mistakes.
>>>
>>> Nathan Sokalski
>>> njsokalski@hotmail.com
>>> ------------------------------
>>> *From:* Joe Weinpert via Discuss <discuss@lists.openscad.org>
>>> *Sent:* Friday, October 31, 2025 2:29 PM
>>> *To:* OpenSCAD general discussion <discuss@lists.openscad.org>
>>> *Cc:* Joe Weinpert <joe.weinpert@gmail.com>
>>> *Subject:* [OpenSCAD] Need a geometry formula
>>>
>>> To all the math wizards out here:
>>>
>>> I need a formula(?) or steps involved in finding the XY centerpoint of a
>>> radius to be tangent to an ellipse.
>>>
>>> Attached pic:
>>>
>>> ellipse size x = 20, y = 9
>>> ellipse centerpoint x = 12, y = 6
>>> fillet dia = 2
>>> fillet centerpoint x = ?, y = 1
>>>
>>> I need to determine where x of the centerpoint will be for the fillet.
>>>
>>>
>>> [image: image.png]
>>>
>>>
>>> Joe Weinpert
>>> joe.weinpert@gmail.com
>>> www.jwstudio.art <http://jwstudio.art>
>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>>

AM
Adrian Mariano
Fri, Oct 31, 2025 10:45 PM
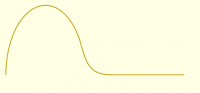
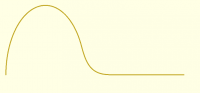
At the risk of talking to myself all night, I'll just also remark that if
the goal is simply to make a fillet from an ellipse to a line an
alternative scheme is to avoid the math and do it from the data
(numerically) like this:
include<BOSL2/std.scad>
ellipse_path = scale([a,b],arc(angle=[180,0],r=1));
smoothpath = path_join([ellipse_path, [[a,0],[a+10,0]]], joint=3);
stroke(smoothpath,width=.1);
Which produces:
[image: image.png]
But the BOSL2 method for this doesn't make a circular rounding, so if
circularity is crucial you'd need a different implementation. (You can get
close with the right k, though.)
On Fri, Oct 31, 2025 at 5:52 PM Adrian Mariano avm4@cornell.edu wrote:
The wrong solution is a circle tangent on the inside of the ellipse.
See below.
[image: image.png]
On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano avm4@cornell.edu wrote:
Looks like it's a bit trickier than shown to select the right root. You
need to ignore negative roots as well, and even then I saw a weird case
where there were two solutions, but one was wrong. So you might need to
actually verify which solution is right if that happens. I don't know the
circumstances that create these various cases.
On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano avm4@cornell.edu wrote:
Below is the solution. I approached the problem like this. Given
ellipse with axes a, b, and desired radius r, suppose y<a. Find the
corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
desired circle is also tangent to the x axis, which means the y component
of its center equals r. That gives you an equation in x and y. The x can
be eliminated using the ellipse equation. Rearrange the terms and you have
a quartic (degree 4) polynomial. Solve that, pick the correct root, and
you're done. I wouldn't call this a simple problem, and finding a strategy
that constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2rk, b^4+r^2k-r^2a^2, -2rb^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
It's been a long time since I took calculus, but here are some steps
that may help:
A derivative, the main topic of calculus, determines the slope of y=f(x)
So your main steps would be to define both your ellipses as a y=f(x)
equation, solve for the derivative, and then solve for where they are
equal. This is probably not the clearest most detailed explanation, but one
thing that I have recently started using a lot for my OpenSCAD geometry is
AI. It gives very good explanations, and you can ask & re-ask the questions
as many times as you want, so nobody will get annoyed with you for being a
pain in the butt, and you don't need to feel embarrassed about asking
little stuff along the way. It will even write some of your code for you if
you ask, so it will majorly speed up some of the work that you used to make
(what feels like) stupid makes missing little mistakes.
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of
a radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
At the risk of talking to myself all night, I'll just also remark that if
the goal is simply to make a fillet from an ellipse to a line an
alternative scheme is to avoid the math and do it from the data
(numerically) like this:
include<BOSL2/std.scad>
ellipse_path = scale([a,b],arc(angle=[180,0],r=1));
smoothpath = path_join([ellipse_path, [[a,0],[a+10,0]]], joint=3);
stroke(smoothpath,width=.1);
Which produces:
[image: image.png]
But the BOSL2 method for this doesn't make a circular rounding, so if
circularity is crucial you'd need a different implementation. (You can get
close with the right k, though.)
On Fri, Oct 31, 2025 at 5:52 PM Adrian Mariano <avm4@cornell.edu> wrote:
> The wrong solution is a circle tangent on the *inside* of the ellipse.
> See below.
>
> [image: image.png]
>
>
> On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano <avm4@cornell.edu> wrote:
>
>> Looks like it's a bit trickier than shown to select the right root. You
>> need to ignore negative roots as well, and even then I saw a weird case
>> where there were two solutions, but one was wrong. So you might need to
>> actually verify which solution is right if that happens. I don't know the
>> circumstances that create these various cases.
>>
>>
>> On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Below is the solution. I approached the problem like this. Given
>>> ellipse with axes a, b, and desired radius r, suppose y<a. Find the
>>> corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
>>> gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
>>> circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
>>> desired circle is also tangent to the x axis, which means the y component
>>> of its center equals r. That gives you an equation in x and y. The x can
>>> be eliminated using the ellipse equation. Rearrange the terms and you have
>>> a quartic (degree 4) polynomial. Solve that, pick the correct root, and
>>> you're done. I wouldn't call this a simple problem, and finding a strategy
>>> that constrains the messiness of the algebra requires some care.
>>>
>>> include<BOSL2/std.scad>
>>>
>>> $fn=120;
>>>
>>> a=10;
>>> b=4;
>>> r=3;
>>>
>>> function find_c(a,b,r,y) =
>>> let(
>>> x2 = a^2*(1-y^2/b^2),
>>> x = sqrt(x2),
>>> n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
>>> c = [x,y] + r*n
>>> )
>>> c;
>>>
>>> k = a^2-b^2;
>>> poly = [k, -2*r*k, b^4+r^2*k-r^2*a^2, -2*r*b^4, r^2*b^4];
>>>
>>> y=[for(p=real_roots(poly)) if (p<b) p];
>>>
>>> echo(y=y);
>>>
>>> if (len(y)==1){
>>> ellipse([a,b]);
>>> move(find_c(a,b,r,y[0]))
>>> circle(r=r);
>>> }
>>> else // This shouldn't happen
>>> echo("failed to find tangent point");
>>>
>>>
>>> On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> It's been a long time since I took calculus, but here are some steps
>>>> that may help:
>>>>
>>>> A derivative, the main topic of calculus, determines the slope of y=f(x)
>>>>
>>>> So your main steps would be to define both your ellipses as a y=f(x)
>>>> equation, solve for the derivative, and then solve for where they are
>>>> equal. This is probably not the clearest most detailed explanation, but one
>>>> thing that I have recently started using a lot for my OpenSCAD geometry is
>>>> AI. It gives very good explanations, and you can ask & re-ask the questions
>>>> as many times as you want, so nobody will get annoyed with you for being a
>>>> pain in the butt, and you don't need to feel embarrassed about asking
>>>> little stuff along the way. It will even write some of your code for you if
>>>> you ask, so it will majorly speed up some of the work that you used to make
>>>> (what feels like) stupid makes missing little mistakes.
>>>>
>>>> Nathan Sokalski
>>>> njsokalski@hotmail.com
>>>> ------------------------------
>>>> *From:* Joe Weinpert via Discuss <discuss@lists.openscad.org>
>>>> *Sent:* Friday, October 31, 2025 2:29 PM
>>>> *To:* OpenSCAD general discussion <discuss@lists.openscad.org>
>>>> *Cc:* Joe Weinpert <joe.weinpert@gmail.com>
>>>> *Subject:* [OpenSCAD] Need a geometry formula
>>>>
>>>> To all the math wizards out here:
>>>>
>>>> I need a formula(?) or steps involved in finding the XY centerpoint of
>>>> a radius to be tangent to an ellipse.
>>>>
>>>> Attached pic:
>>>>
>>>> ellipse size x = 20, y = 9
>>>> ellipse centerpoint x = 12, y = 6
>>>> fillet dia = 2
>>>> fillet centerpoint x = ?, y = 1
>>>>
>>>> I need to determine where x of the centerpoint will be for the fillet.
>>>>
>>>>
>>>> [image: image.png]
>>>>
>>>>
>>>> Joe Weinpert
>>>> joe.weinpert@gmail.com
>>>> www.jwstudio.art <http://jwstudio.art>
>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>
>>>

JW
Joe Weinpert
Fri, Oct 31, 2025 10:57 PM
At the risk of talking to myself all night, I'll just also remark that if
the goal is simply to make a fillet from an ellipse to a line an
alternative scheme is to avoid the math and do it from the data
(numerically) like this:
include<BOSL2/std.scad>
ellipse_path = scale([a,b],arc(angle=[180,0],r=1));
smoothpath = path_join([ellipse_path, [[a,0],[a+10,0]]], joint=3);
stroke(smoothpath,width=.1);
Which produces:
[image: image.png]
But the BOSL2 method for this doesn't make a circular rounding, so if
circularity is crucial you'd need a different implementation. (You can get
close with the right k, though.)
On Fri, Oct 31, 2025 at 5:52 PM Adrian Mariano avm4@cornell.edu wrote:
The wrong solution is a circle tangent on the inside of the ellipse.
See below.
[image: image.png]
On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano avm4@cornell.edu wrote:
Looks like it's a bit trickier than shown to select the right root. You
need to ignore negative roots as well, and even then I saw a weird case
where there were two solutions, but one was wrong. So you might need to
actually verify which solution is right if that happens. I don't know the
circumstances that create these various cases.
On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano avm4@cornell.edu wrote:
Below is the solution. I approached the problem like this. Given
ellipse with axes a, b, and desired radius r, suppose y<a. Find the
corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
desired circle is also tangent to the x axis, which means the y component
of its center equals r. That gives you an equation in x and y. The x can
be eliminated using the ellipse equation. Rearrange the terms and you have
a quartic (degree 4) polynomial. Solve that, pick the correct root, and
you're done. I wouldn't call this a simple problem, and finding a strategy
that constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2rk, b^4+r^2k-r^2a^2, -2rb^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
It's been a long time since I took calculus, but here are some steps
that may help:
A derivative, the main topic of calculus, determines the slope of
y=f(x)
So your main steps would be to define both your ellipses as a y=f(x)
equation, solve for the derivative, and then solve for where they are
equal. This is probably not the clearest most detailed explanation, but one
thing that I have recently started using a lot for my OpenSCAD geometry is
AI. It gives very good explanations, and you can ask & re-ask the questions
as many times as you want, so nobody will get annoyed with you for being a
pain in the butt, and you don't need to feel embarrassed about asking
little stuff along the way. It will even write some of your code for you if
you ask, so it will majorly speed up some of the work that you used to make
(what feels like) stupid makes missing little mistakes.
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of
a radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Just got back to my shop. My head is spinning after reading the
answers!!! 😏 It is much more difficult than I imagined!
I truly appreciate the answers and will examine them all again.
Joe Weinpert
(440) 796-7165
joe.weinpert@gmail.com
www.jwstudio.art <http://jwstudio.art>
On Fri, Oct 31, 2025 at 6:46 PM Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
> At the risk of talking to myself all night, I'll just also remark that if
> the goal is simply to make a fillet from an ellipse to a line an
> alternative scheme is to avoid the math and do it from the data
> (numerically) like this:
>
> include<BOSL2/std.scad>
>
> ellipse_path = scale([a,b],arc(angle=[180,0],r=1));
> smoothpath = path_join([ellipse_path, [[a,0],[a+10,0]]], joint=3);
> stroke(smoothpath,width=.1);
>
> Which produces:
>
> [image: image.png]
>
> But the BOSL2 method for this doesn't make a circular rounding, so if
> circularity is crucial you'd need a different implementation. (You can get
> close with the right k, though.)
>
> On Fri, Oct 31, 2025 at 5:52 PM Adrian Mariano <avm4@cornell.edu> wrote:
>
>> The wrong solution is a circle tangent on the *inside* of the ellipse.
>> See below.
>>
>> [image: image.png]
>>
>>
>> On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> Looks like it's a bit trickier than shown to select the right root. You
>>> need to ignore negative roots as well, and even then I saw a weird case
>>> where there were two solutions, but one was wrong. So you might need to
>>> actually verify which solution is right if that happens. I don't know the
>>> circumstances that create these various cases.
>>>
>>>
>>> On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> Below is the solution. I approached the problem like this. Given
>>>> ellipse with axes a, b, and desired radius r, suppose y<a. Find the
>>>> corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
>>>> gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
>>>> circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
>>>> desired circle is also tangent to the x axis, which means the y component
>>>> of its center equals r. That gives you an equation in x and y. The x can
>>>> be eliminated using the ellipse equation. Rearrange the terms and you have
>>>> a quartic (degree 4) polynomial. Solve that, pick the correct root, and
>>>> you're done. I wouldn't call this a simple problem, and finding a strategy
>>>> that constrains the messiness of the algebra requires some care.
>>>>
>>>> include<BOSL2/std.scad>
>>>>
>>>> $fn=120;
>>>>
>>>> a=10;
>>>> b=4;
>>>> r=3;
>>>>
>>>> function find_c(a,b,r,y) =
>>>> let(
>>>> x2 = a^2*(1-y^2/b^2),
>>>> x = sqrt(x2),
>>>> n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
>>>> c = [x,y] + r*n
>>>> )
>>>> c;
>>>>
>>>> k = a^2-b^2;
>>>> poly = [k, -2*r*k, b^4+r^2*k-r^2*a^2, -2*r*b^4, r^2*b^4];
>>>>
>>>> y=[for(p=real_roots(poly)) if (p<b) p];
>>>>
>>>> echo(y=y);
>>>>
>>>> if (len(y)==1){
>>>> ellipse([a,b]);
>>>> move(find_c(a,b,r,y[0]))
>>>> circle(r=r);
>>>> }
>>>> else // This shouldn't happen
>>>> echo("failed to find tangent point");
>>>>
>>>>
>>>> On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
>>>> discuss@lists.openscad.org> wrote:
>>>>
>>>>> It's been a long time since I took calculus, but here are some steps
>>>>> that may help:
>>>>>
>>>>> A derivative, the main topic of calculus, determines the slope of
>>>>> y=f(x)
>>>>>
>>>>> So your main steps would be to define both your ellipses as a y=f(x)
>>>>> equation, solve for the derivative, and then solve for where they are
>>>>> equal. This is probably not the clearest most detailed explanation, but one
>>>>> thing that I have recently started using a lot for my OpenSCAD geometry is
>>>>> AI. It gives very good explanations, and you can ask & re-ask the questions
>>>>> as many times as you want, so nobody will get annoyed with you for being a
>>>>> pain in the butt, and you don't need to feel embarrassed about asking
>>>>> little stuff along the way. It will even write some of your code for you if
>>>>> you ask, so it will majorly speed up some of the work that you used to make
>>>>> (what feels like) stupid makes missing little mistakes.
>>>>>
>>>>> Nathan Sokalski
>>>>> njsokalski@hotmail.com
>>>>> ------------------------------
>>>>> *From:* Joe Weinpert via Discuss <discuss@lists.openscad.org>
>>>>> *Sent:* Friday, October 31, 2025 2:29 PM
>>>>> *To:* OpenSCAD general discussion <discuss@lists.openscad.org>
>>>>> *Cc:* Joe Weinpert <joe.weinpert@gmail.com>
>>>>> *Subject:* [OpenSCAD] Need a geometry formula
>>>>>
>>>>> To all the math wizards out here:
>>>>>
>>>>> I need a formula(?) or steps involved in finding the XY centerpoint of
>>>>> a radius to be tangent to an ellipse.
>>>>>
>>>>> Attached pic:
>>>>>
>>>>> ellipse size x = 20, y = 9
>>>>> ellipse centerpoint x = 12, y = 6
>>>>> fillet dia = 2
>>>>> fillet centerpoint x = ?, y = 1
>>>>>
>>>>> I need to determine where x of the centerpoint will be for the fillet.
>>>>>
>>>>>
>>>>> [image: image.png]
>>>>>
>>>>>
>>>>> Joe Weinpert
>>>>> joe.weinpert@gmail.com
>>>>> www.jwstudio.art <http://jwstudio.art>
>>>>>
>>>>> _______________________________________________
>>>>> OpenSCAD mailing list
>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>
>>>> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

AM
Adrian Mariano
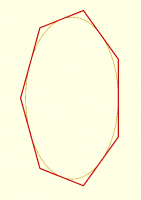
Fri, Oct 31, 2025 11:26 PM
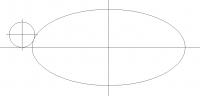
Geometric problems tend to get messy really fast. Most problems that
involve ellipses are already very messy. Consider that computing arc
length of a section of an ellipse cannot be done without an
iterative method (you need to evaluate an "elliptic integral"). This is
one of the attractions of the sort of approach I showed using join_path
where the calculation is done numerically on samples of the path instead of
mathematically on the ideal path. It works on every case and is fairly
easy to implement, less complicated than working out the math for the
ellipse case I would say.
I tried to write code for BOSL2 to compute an N segment approximation to an
ellipse the way that you can do circle($fn=7) and get a regular 7-gon.
This is trivial for the circle. What if you want the ellipse equivalent?
I managed to implement this for the case of an inscribed polygon as shown
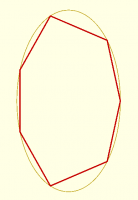
below, with all sides the same length, but it required an iterative
algorithm.
[image: image.png]
But for the case of the circumscribed polygon, I can't even get an
iterative algorithm that always works. Here's what the circumscribed case
looks like with non-uniform side lengths:
But for the case of the circumscribed polygon, I can't even get an
iterative algorithm that always works. In the circle case the inscribed
and circumscribed polygon are congruent, just different sizes. But for the
ellipse that's not true. The circumscribed polygon is a completely
different shape.
[image: image.png]
These examples are all from the BOSL2 ellipse() function/module.
On Fri, Oct 31, 2025 at 6:58 PM Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
At the risk of talking to myself all night, I'll just also remark that if
the goal is simply to make a fillet from an ellipse to a line an
alternative scheme is to avoid the math and do it from the data
(numerically) like this:
include<BOSL2/std.scad>
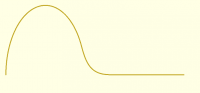
ellipse_path = scale([a,b],arc(angle=[180,0],r=1));
smoothpath = path_join([ellipse_path, [[a,0],[a+10,0]]], joint=3);
stroke(smoothpath,width=.1);
Which produces:
[image: image.png]
But the BOSL2 method for this doesn't make a circular rounding, so if
circularity is crucial you'd need a different implementation. (You can get
close with the right k, though.)
On Fri, Oct 31, 2025 at 5:52 PM Adrian Mariano avm4@cornell.edu wrote:
The wrong solution is a circle tangent on the inside of the ellipse.
See below.
[image: image.png]
On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano avm4@cornell.edu wrote:
Looks like it's a bit trickier than shown to select the right root.
You need to ignore negative roots as well, and even then I saw a weird case
where there were two solutions, but one was wrong. So you might need to
actually verify which solution is right if that happens. I don't know the
circumstances that create these various cases.
On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano avm4@cornell.edu
wrote:
Below is the solution. I approached the problem like this. Given
ellipse with axes a, b, and desired radius r, suppose y<a. Find the
corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
desired circle is also tangent to the x axis, which means the y component
of its center equals r. That gives you an equation in x and y. The x can
be eliminated using the ellipse equation. Rearrange the terms and you have
a quartic (degree 4) polynomial. Solve that, pick the correct root, and
you're done. I wouldn't call this a simple problem, and finding a strategy
that constrains the messiness of the algebra requires some care.
include<BOSL2/std.scad>
$fn=120;
a=10;
b=4;
r=3;
function find_c(a,b,r,y) =
let(
x2 = a^2*(1-y^2/b^2),
x = sqrt(x2),
n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
c = [x,y] + r*n
)
c;
k = a^2-b^2;
poly = [k, -2rk, b^4+r^2k-r^2a^2, -2rb^4, r^2*b^4];
y=[for(p=real_roots(poly)) if (p<b) p];
echo(y=y);
if (len(y)==1){
ellipse([a,b]);
move(find_c(a,b,r,y[0]))
circle(r=r);
}
else // This shouldn't happen
echo("failed to find tangent point");
On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
discuss@lists.openscad.org> wrote:
It's been a long time since I took calculus, but here are some steps
that may help:
A derivative, the main topic of calculus, determines the slope of
y=f(x)
So your main steps would be to define both your ellipses as a y=f(x)
equation, solve for the derivative, and then solve for where they are
equal. This is probably not the clearest most detailed explanation, but one
thing that I have recently started using a lot for my OpenSCAD geometry is
AI. It gives very good explanations, and you can ask & re-ask the questions
as many times as you want, so nobody will get annoyed with you for being a
pain in the butt, and you don't need to feel embarrassed about asking
little stuff along the way. It will even write some of your code for you if
you ask, so it will majorly speed up some of the work that you used to make
(what feels like) stupid makes missing little mistakes.
From: Joe Weinpert via Discuss discuss@lists.openscad.org
Sent: Friday, October 31, 2025 2:29 PM
To: OpenSCAD general discussion discuss@lists.openscad.org
Cc: Joe Weinpert joe.weinpert@gmail.com
Subject: [OpenSCAD] Need a geometry formula
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint
of a radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Geometric problems tend to get messy really fast. Most problems that
involve ellipses are already very messy. Consider that computing arc
length of a section of an ellipse cannot be done without an
iterative method (you need to evaluate an "elliptic integral"). This is
one of the attractions of the sort of approach I showed using join_path
where the calculation is done numerically on samples of the path instead of
mathematically on the ideal path. It works on every case and is fairly
easy to implement, less complicated than working out the math for the
ellipse case I would say.
I tried to write code for BOSL2 to compute an N segment approximation to an
ellipse the way that you can do circle($fn=7) and get a regular 7-gon.
This is trivial for the circle. What if you want the ellipse equivalent?
I managed to implement this for the case of an inscribed polygon as shown
below, with all sides the same length, but it required an iterative
algorithm.
[image: image.png]
But for the case of the circumscribed polygon, I can't even get an
iterative algorithm that always works. Here's what the circumscribed case
looks like with non-uniform side lengths:
But for the case of the circumscribed polygon, I can't even get an
iterative algorithm that always works. In the circle case the inscribed
and circumscribed polygon are congruent, just different sizes. But for the
ellipse that's not true. The circumscribed polygon is a completely
different shape.
[image: image.png]
These examples are all from the BOSL2 ellipse() function/module.
On Fri, Oct 31, 2025 at 6:58 PM Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
> Just got back to my shop. My head is spinning after reading the
> answers!!! 😏 It is much more difficult than I imagined!
> I truly appreciate the answers and will examine them all again.
>
>
>
>
> Joe Weinpert
> (440) 796-7165
> joe.weinpert@gmail.com
> www.jwstudio.art <http://jwstudio.art>
>
>
>
> On Fri, Oct 31, 2025 at 6:46 PM Adrian Mariano via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> At the risk of talking to myself all night, I'll just also remark that if
>> the goal is simply to make a fillet from an ellipse to a line an
>> alternative scheme is to avoid the math and do it from the data
>> (numerically) like this:
>>
>> include<BOSL2/std.scad>
>>
>> ellipse_path = scale([a,b],arc(angle=[180,0],r=1));
>> smoothpath = path_join([ellipse_path, [[a,0],[a+10,0]]], joint=3);
>> stroke(smoothpath,width=.1);
>>
>> Which produces:
>>
>> [image: image.png]
>>
>> But the BOSL2 method for this doesn't make a circular rounding, so if
>> circularity is crucial you'd need a different implementation. (You can get
>> close with the right k, though.)
>>
>> On Fri, Oct 31, 2025 at 5:52 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>
>>> The wrong solution is a circle tangent on the *inside* of the ellipse.
>>> See below.
>>>
>>> [image: image.png]
>>>
>>>
>>> On Fri, Oct 31, 2025 at 5:00 PM Adrian Mariano <avm4@cornell.edu> wrote:
>>>
>>>> Looks like it's a bit trickier than shown to select the right root.
>>>> You need to ignore negative roots as well, and even then I saw a weird case
>>>> where there were two solutions, but one was wrong. So you might need to
>>>> actually verify which solution is right if that happens. I don't know the
>>>> circumstances that create these various cases.
>>>>
>>>>
>>>> On Fri, Oct 31, 2025 at 4:40 PM Adrian Mariano <avm4@cornell.edu>
>>>> wrote:
>>>>
>>>>> Below is the solution. I approached the problem like this. Given
>>>>> ellipse with axes a, b, and desired radius r, suppose y<a. Find the
>>>>> corresponding point x so that (x,y) is on the ellipse (in quadrant 1). The
>>>>> gradient of the ellipse equation is n = 2(x/a^2,y/b^2). The center of a
>>>>> circle that is tangent to the ellipse at (x,y) is (x,y)+r*n/norm(n). The
>>>>> desired circle is also tangent to the x axis, which means the y component
>>>>> of its center equals r. That gives you an equation in x and y. The x can
>>>>> be eliminated using the ellipse equation. Rearrange the terms and you have
>>>>> a quartic (degree 4) polynomial. Solve that, pick the correct root, and
>>>>> you're done. I wouldn't call this a simple problem, and finding a strategy
>>>>> that constrains the messiness of the algebra requires some care.
>>>>>
>>>>> include<BOSL2/std.scad>
>>>>>
>>>>> $fn=120;
>>>>>
>>>>> a=10;
>>>>> b=4;
>>>>> r=3;
>>>>>
>>>>> function find_c(a,b,r,y) =
>>>>> let(
>>>>> x2 = a^2*(1-y^2/b^2),
>>>>> x = sqrt(x2),
>>>>> n = [x/a^2,y/b^2] / sqrt(x^2/a^4+y^2/b^4),
>>>>> c = [x,y] + r*n
>>>>> )
>>>>> c;
>>>>>
>>>>> k = a^2-b^2;
>>>>> poly = [k, -2*r*k, b^4+r^2*k-r^2*a^2, -2*r*b^4, r^2*b^4];
>>>>>
>>>>> y=[for(p=real_roots(poly)) if (p<b) p];
>>>>>
>>>>> echo(y=y);
>>>>>
>>>>> if (len(y)==1){
>>>>> ellipse([a,b]);
>>>>> move(find_c(a,b,r,y[0]))
>>>>> circle(r=r);
>>>>> }
>>>>> else // This shouldn't happen
>>>>> echo("failed to find tangent point");
>>>>>
>>>>>
>>>>> On Fri, Oct 31, 2025 at 3:37 PM Nathan Sokalski via Discuss <
>>>>> discuss@lists.openscad.org> wrote:
>>>>>
>>>>>> It's been a long time since I took calculus, but here are some steps
>>>>>> that may help:
>>>>>>
>>>>>> A derivative, the main topic of calculus, determines the slope of
>>>>>> y=f(x)
>>>>>>
>>>>>> So your main steps would be to define both your ellipses as a y=f(x)
>>>>>> equation, solve for the derivative, and then solve for where they are
>>>>>> equal. This is probably not the clearest most detailed explanation, but one
>>>>>> thing that I have recently started using a lot for my OpenSCAD geometry is
>>>>>> AI. It gives very good explanations, and you can ask & re-ask the questions
>>>>>> as many times as you want, so nobody will get annoyed with you for being a
>>>>>> pain in the butt, and you don't need to feel embarrassed about asking
>>>>>> little stuff along the way. It will even write some of your code for you if
>>>>>> you ask, so it will majorly speed up some of the work that you used to make
>>>>>> (what feels like) stupid makes missing little mistakes.
>>>>>>
>>>>>> Nathan Sokalski
>>>>>> njsokalski@hotmail.com
>>>>>> ------------------------------
>>>>>> *From:* Joe Weinpert via Discuss <discuss@lists.openscad.org>
>>>>>> *Sent:* Friday, October 31, 2025 2:29 PM
>>>>>> *To:* OpenSCAD general discussion <discuss@lists.openscad.org>
>>>>>> *Cc:* Joe Weinpert <joe.weinpert@gmail.com>
>>>>>> *Subject:* [OpenSCAD] Need a geometry formula
>>>>>>
>>>>>> To all the math wizards out here:
>>>>>>
>>>>>> I need a formula(?) or steps involved in finding the XY centerpoint
>>>>>> of a radius to be tangent to an ellipse.
>>>>>>
>>>>>> Attached pic:
>>>>>>
>>>>>> ellipse size x = 20, y = 9
>>>>>> ellipse centerpoint x = 12, y = 6
>>>>>> fillet dia = 2
>>>>>> fillet centerpoint x = ?, y = 1
>>>>>>
>>>>>> I need to determine where x of the centerpoint will be for the fillet.
>>>>>>
>>>>>>
>>>>>> [image: image.png]
>>>>>>
>>>>>>
>>>>>> Joe Weinpert
>>>>>> joe.weinpert@gmail.com
>>>>>> www.jwstudio.art <http://jwstudio.art>
>>>>>>
>>>>>> _______________________________________________
>>>>>> OpenSCAD mailing list
>>>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>>>>
>>>>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

FH
Father Horton
Fri, Oct 31, 2025 11:36 PM
Ramanujan found approximations for the perimeter of an ellipse that are
quite close to the actual answer. Since it’s Ramanujan, no one knows why
they work, but they do.
Ramanujan found approximations for the perimeter of an ellipse that are
quite close to the actual answer. Since it’s Ramanujan, no one knows why
they work, but they do.