AM
Adrian Mariano
Fri, Oct 31, 2025 11:51 PM
I think Ramanujan's formula only gives you the total perimeter, not the arc
length between two points, which is the sort of thing you'd likely need for
working out geometric algorithms. Like the code I mentioned above takes a
"joint" parameter and it moves back along the arc by that specified
distance to decide where to start the joining fillet. That requires
solving for arclength over just part of the ellipse.
On Fri, Oct 31, 2025 at 7:36 PM Father Horton fatherhorton@gmail.com
wrote:
Ramanujan found approximations for the perimeter of an ellipse that are
quite close to the actual answer. Since it’s Ramanujan, no one knows why
they work, but they do.
I think Ramanujan's formula only gives you the total perimeter, not the arc
length between two points, which is the sort of thing you'd likely need for
working out geometric algorithms. Like the code I mentioned above takes a
"joint" parameter and it moves back along the arc by that specified
distance to decide where to start the joining fillet. That requires
solving for arclength over just part of the ellipse.
On Fri, Oct 31, 2025 at 7:36 PM Father Horton <fatherhorton@gmail.com>
wrote:
> Ramanujan found approximations for the perimeter of an ellipse that are
> quite close to the actual answer. Since it’s Ramanujan, no one knows why
> they work, but they do.

JW
Joe Weinpert
Sat, Nov 1, 2025 12:48 AM
I think Ramanujan's formula only gives you the total perimeter, not the
arc length between two points, which is the sort of thing you'd likely need
for working out geometric algorithms. Like the code I mentioned above
takes a "joint" parameter and it moves back along the arc by that specified
distance to decide where to start the joining fillet. That requires
solving for arclength over just part of the ellipse.
On Fri, Oct 31, 2025 at 7:36 PM Father Horton fatherhorton@gmail.com
wrote:
Ramanujan found approximations for the perimeter of an ellipse that are
quite close to the actual answer. Since it’s Ramanujan, no one knows why
they work, but they do.
I am beginning to understand the need to "slide" an object like a circle
along an axis until it collides with the object to determine the
centerpoint for the fillet.
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art <http://jwstudio.art>
On Fri, Oct 31, 2025, 7:52 PM Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
> I think Ramanujan's formula only gives you the total perimeter, not the
> arc length between two points, which is the sort of thing you'd likely need
> for working out geometric algorithms. Like the code I mentioned above
> takes a "joint" parameter and it moves back along the arc by that specified
> distance to decide where to start the joining fillet. That requires
> solving for arclength over just part of the ellipse.
>
> On Fri, Oct 31, 2025 at 7:36 PM Father Horton <fatherhorton@gmail.com>
> wrote:
>
>> Ramanujan found approximations for the perimeter of an ellipse that are
>> quite close to the actual answer. Since it’s Ramanujan, no one knows why
>> they work, but they do.
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

SP
Sanjeev Prabhakar
Sat, Nov 1, 2025 1:46 AM
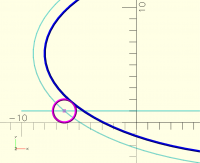
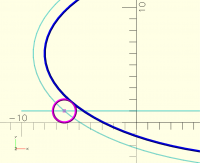
To find equation for this would not be a trivial task.
general steps as per me would be:
offset the ellipse by radius of circle, so that the center of circle lies
in this line
now offset both circle and ellipse by the amount of fillet
find the intersection point between these 2 to get the center point fillet
circle.
Solving this by an equation would be difficult because offset of an ellipse
is not an ellipse.
[image: Screenshot 2025-11-01 at 7.15.40 AM.png]
On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
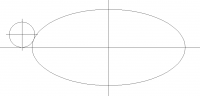
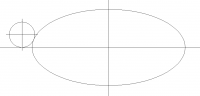
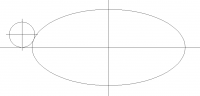
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
To find equation for this would not be a trivial task.
general steps as per me would be:
offset the ellipse by radius of circle, so that the center of circle lies
in this line
now offset both circle and ellipse by the amount of fillet
find the intersection point between these 2 to get the center point fillet
circle.
Solving this by an equation would be difficult because offset of an ellipse
is not an ellipse.
[image: Screenshot 2025-11-01 at 7.15.40 AM.png]
On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
> To all the math wizards out here:
>
> I need a formula(?) or steps involved in finding the XY centerpoint of a
> radius to be tangent to an ellipse.
>
> Attached pic:
>
> ellipse size x = 20, y = 9
> ellipse centerpoint x = 12, y = 6
> fillet dia = 2
> fillet centerpoint x = ?, y = 1
>
> I need to determine where x of the centerpoint will be for the fillet.
>
>
> [image: image.png]
>
>
> Joe Weinpert
> joe.weinpert@gmail.com
> www.jwstudio.art <http://jwstudio.art>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org


SP
Sanjeev Prabhakar
Sat, Nov 1, 2025 3:46 AM
I think i missed your point
You simply need a circle tangent to a point on ellipse at y=1
this should not be too difficult
need to calculate a slope at point in question [x,1] for the equation of
ellipse i.e. x^2/a^2+y^2/b^2=1
dy/dy = -b^2/a^a*x/y
once you have the slope, it should be easier to calculate the tangent
circle.
Maybe i will try in the evening
On Sat, 1 Nov 2025 at 07:16, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
To find equation for this would not be a trivial task.
general steps as per me would be:
offset the ellipse by radius of circle, so that the center of circle lies
in this line
now offset both circle and ellipse by the amount of fillet
find the intersection point between these 2 to get the center point fillet
circle.
Solving this by an equation would be difficult because offset of an
ellipse is not an ellipse.
[image: Screenshot 2025-11-01 at 7.15.40 AM.png]
On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I think i missed your point
You simply need a circle tangent to a point on ellipse at y=1
this should not be too difficult
need to calculate a slope at point in question [x,1] for the equation of
ellipse i.e. x^2/a^2+y^2/b^2=1
dy/dy = -b^2/a^a*x/y
once you have the slope, it should be easier to calculate the tangent
circle.
Maybe i will try in the evening
On Sat, 1 Nov 2025 at 07:16, Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> To find equation for this would not be a trivial task.
> general steps as per me would be:
> offset the ellipse by radius of circle, so that the center of circle lies
> in this line
> now offset both circle and ellipse by the amount of fillet
> find the intersection point between these 2 to get the center point fillet
> circle.
>
> Solving this by an equation would be difficult because offset of an
> ellipse is not an ellipse.
> [image: Screenshot 2025-11-01 at 7.15.40 AM.png]
>
>
> On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
> discuss@lists.openscad.org> wrote:
>
>> To all the math wizards out here:
>>
>> I need a formula(?) or steps involved in finding the XY centerpoint of a
>> radius to be tangent to an ellipse.
>>
>> Attached pic:
>>
>> ellipse size x = 20, y = 9
>> ellipse centerpoint x = 12, y = 6
>> fillet dia = 2
>> fillet centerpoint x = ?, y = 1
>>
>> I need to determine where x of the centerpoint will be for the fillet.
>>
>>
>> [image: image.png]
>>
>>
>> Joe Weinpert
>> joe.weinpert@gmail.com
>> www.jwstudio.art <http://jwstudio.art>
>>
>> _______________________________________________
>> OpenSCAD mailing list
>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
>


SP
Sanjeev Prabhakar
Sat, Nov 1, 2025 1:53 PM
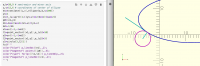
Here is the explanation attached and this is a generic solution.
This can be also done in openscad for values of y, based on the semi-major
and minor axis and center point of ellipse.
here in the below screen shot
a,b are the semi-major and minor axis
u,v are the coordinates of center of ellipse
all the calculations done by hand but can be easily done by computer
[image: Screenshot 2025-11-01 at 7.18.57 PM.png]
On Sat, 1 Nov 2025 at 09:16, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I think i missed your point
You simply need a circle tangent to a point on ellipse at y=1
this should not be too difficult
need to calculate a slope at point in question [x,1] for the equation of
ellipse i.e. x^2/a^2+y^2/b^2=1
dy/dy = -b^2/a^a*x/y
once you have the slope, it should be easier to calculate the tangent
circle.
Maybe i will try in the evening
On Sat, 1 Nov 2025 at 07:16, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
To find equation for this would not be a trivial task.
general steps as per me would be:
offset the ellipse by radius of circle, so that the center of circle lies
in this line
now offset both circle and ellipse by the amount of fillet
find the intersection point between these 2 to get the center point
fillet circle.
Solving this by an equation would be difficult because offset of an
ellipse is not an ellipse.
[image: Screenshot 2025-11-01 at 7.15.40 AM.png]
On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of a
radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Here is the explanation attached and this is a generic solution.
This can be also done in openscad for values of y, based on the semi-major
and minor axis and center point of ellipse.
here in the below screen shot
a,b are the semi-major and minor axis
u,v are the coordinates of center of ellipse
all the calculations done by hand but can be easily done by computer
[image: Screenshot 2025-11-01 at 7.18.57 PM.png]
On Sat, 1 Nov 2025 at 09:16, Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> I think i missed your point
> You simply need a circle tangent to a point on ellipse at y=1
> this should not be too difficult
> need to calculate a slope at point in question [x,1] for the equation of
> ellipse i.e. x^2/a^2+y^2/b^2=1
> dy/dy = -b^2/a^a*x/y
> once you have the slope, it should be easier to calculate the tangent
> circle.
> Maybe i will try in the evening
>
>
> On Sat, 1 Nov 2025 at 07:16, Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> To find equation for this would not be a trivial task.
>> general steps as per me would be:
>> offset the ellipse by radius of circle, so that the center of circle lies
>> in this line
>> now offset both circle and ellipse by the amount of fillet
>> find the intersection point between these 2 to get the center point
>> fillet circle.
>>
>> Solving this by an equation would be difficult because offset of an
>> ellipse is not an ellipse.
>> [image: Screenshot 2025-11-01 at 7.15.40 AM.png]
>>
>>
>> On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
>> discuss@lists.openscad.org> wrote:
>>
>>> To all the math wizards out here:
>>>
>>> I need a formula(?) or steps involved in finding the XY centerpoint of a
>>> radius to be tangent to an ellipse.
>>>
>>> Attached pic:
>>>
>>> ellipse size x = 20, y = 9
>>> ellipse centerpoint x = 12, y = 6
>>> fillet dia = 2
>>> fillet centerpoint x = ?, y = 1
>>>
>>> I need to determine where x of the centerpoint will be for the fillet.
>>>
>>>
>>> [image: image.png]
>>>
>>>
>>> Joe Weinpert
>>> joe.weinpert@gmail.com
>>> www.jwstudio.art <http://jwstudio.art>
>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>
>>

AM
Adrian Mariano
Sat, Nov 1, 2025 2:15 PM
Sanjeev, maybe I'm missing something, but it appears that your analysis
finds the circle tangent to an ellipse AT A GIVEN POINT. This is indeed a
fairly straight forward problem---but it's not the one that was posed. The
problem at hand is to determine the centerpoint of a circle that is
simultaneously tangent to a (centered) ellipse and the X axis. The point
on the ellipse is not known---in fact, determining that point is the whole
problem, because then the center of the circle is easy to find as you
note.
On Sat, Nov 1, 2025 at 9:54 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
Here is the explanation attached and this is a generic solution.
This can be also done in openscad for values of y, based on the semi-major
and minor axis and center point of ellipse.
here in the below screen shot
a,b are the semi-major and minor axis
u,v are the coordinates of center of ellipse
all the calculations done by hand but can be easily done by computer
[image: Screenshot 2025-11-01 at 7.18.57 PM.png]
On Sat, 1 Nov 2025 at 09:16, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
I think i missed your point
You simply need a circle tangent to a point on ellipse at y=1
this should not be too difficult
need to calculate a slope at point in question [x,1] for the equation of
ellipse i.e. x^2/a^2+y^2/b^2=1
dy/dy = -b^2/a^a*x/y
once you have the slope, it should be easier to calculate the tangent
circle.
Maybe i will try in the evening
On Sat, 1 Nov 2025 at 07:16, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
To find equation for this would not be a trivial task.
general steps as per me would be:
offset the ellipse by radius of circle, so that the center of circle
lies in this line
now offset both circle and ellipse by the amount of fillet
find the intersection point between these 2 to get the center point
fillet circle.
Solving this by an equation would be difficult because offset of an
ellipse is not an ellipse.
[image: Screenshot 2025-11-01 at 7.15.40 AM.png]
On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
To all the math wizards out here:
I need a formula(?) or steps involved in finding the XY centerpoint of
a radius to be tangent to an ellipse.
Attached pic:
ellipse size x = 20, y = 9
ellipse centerpoint x = 12, y = 6
fillet dia = 2
fillet centerpoint x = ?, y = 1
I need to determine where x of the centerpoint will be for the fillet.
[image: image.png]
Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Sanjeev, maybe I'm missing something, but it appears that your analysis
finds the circle tangent to an ellipse AT A GIVEN POINT. This is indeed a
fairly straight forward problem---but it's not the one that was posed. The
problem at hand is to determine the centerpoint of a circle that is
simultaneously tangent to a (centered) ellipse and the X axis. The point
on the ellipse is not known---in fact, determining that point is the whole
problem, because then the center of the circle is easy to find as you
note.
On Sat, Nov 1, 2025 at 9:54 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
> Here is the explanation attached and this is a generic solution.
> This can be also done in openscad for values of y, based on the semi-major
> and minor axis and center point of ellipse.
> here in the below screen shot
> a,b are the semi-major and minor axis
> u,v are the coordinates of center of ellipse
> all the calculations done by hand but can be easily done by computer
> [image: Screenshot 2025-11-01 at 7.18.57 PM.png]
>
> On Sat, 1 Nov 2025 at 09:16, Sanjeev Prabhakar <sprabhakar2006@gmail.com>
> wrote:
>
>> I think i missed your point
>> You simply need a circle tangent to a point on ellipse at y=1
>> this should not be too difficult
>> need to calculate a slope at point in question [x,1] for the equation of
>> ellipse i.e. x^2/a^2+y^2/b^2=1
>> dy/dy = -b^2/a^a*x/y
>> once you have the slope, it should be easier to calculate the tangent
>> circle.
>> Maybe i will try in the evening
>>
>>
>> On Sat, 1 Nov 2025 at 07:16, Sanjeev Prabhakar <sprabhakar2006@gmail.com>
>> wrote:
>>
>>> To find equation for this would not be a trivial task.
>>> general steps as per me would be:
>>> offset the ellipse by radius of circle, so that the center of circle
>>> lies in this line
>>> now offset both circle and ellipse by the amount of fillet
>>> find the intersection point between these 2 to get the center point
>>> fillet circle.
>>>
>>> Solving this by an equation would be difficult because offset of an
>>> ellipse is not an ellipse.
>>> [image: Screenshot 2025-11-01 at 7.15.40 AM.png]
>>>
>>>
>>> On Sat, 1 Nov 2025 at 00:00, Joe Weinpert via Discuss <
>>> discuss@lists.openscad.org> wrote:
>>>
>>>> To all the math wizards out here:
>>>>
>>>> I need a formula(?) or steps involved in finding the XY centerpoint of
>>>> a radius to be tangent to an ellipse.
>>>>
>>>> Attached pic:
>>>>
>>>> ellipse size x = 20, y = 9
>>>> ellipse centerpoint x = 12, y = 6
>>>> fillet dia = 2
>>>> fillet centerpoint x = ?, y = 1
>>>>
>>>> I need to determine where x of the centerpoint will be for the fillet.
>>>>
>>>>
>>>> [image: image.png]
>>>>
>>>>
>>>> Joe Weinpert
>>>> joe.weinpert@gmail.com
>>>> www.jwstudio.art <http://jwstudio.art>
>>>>
>>>> _______________________________________________
>>>> OpenSCAD mailing list
>>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
>>>
>>> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

SP
Sanjeev Prabhakar
Sat, Nov 1, 2025 4:49 PM
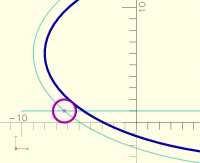
In the initial posting I could not find any such requirement.
The picture shown and the description is a little different it seems and
might have caused this confusion.
Description says the ellipse center is at [12,6] whereas the center of the
ellipse in the picture appears to be at the origin.
This would be very tedious to solve
there would be 2 equations here to solve for this intersection:
(x-a)^2+(y-1)^2=1 --> eq1
(x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
once the intersection point is calculated, rest is simpler
Manually maybe impossible. Need to see if this could be solved through
computer.
but in that case easier solution would be:
draw an offset to ellipse
draw a horizontal line at y=1
find intersection between the two and that is the center point
as per my calculation for this case it is : [-6.28385, 1. ]
[image: Screenshot 2025-11-01 at 10.02.47 PM.png]
In the initial posting I could not find any such requirement.
The picture shown and the description is a little different it seems and
might have caused this confusion.
Description says the ellipse center is at [12,6] whereas the center of the
ellipse in the picture appears to be at the origin.
This would be very tedious to solve
there would be 2 equations here to solve for this intersection:
(x-a)^2+(y-1)^2=1 --> eq1
(x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
once the intersection point is calculated, rest is simpler
Manually maybe impossible. Need to see if this could be solved through
computer.
but in that case easier solution would be:
draw an offset to ellipse
draw a horizontal line at y=1
find intersection between the two and that is the center point
as per my calculation for this case it is : [-6.28385, 1. ]
[image: Screenshot 2025-11-01 at 10.02.47 PM.png]

AM
Adrian Mariano
Sat, Nov 1, 2025 5:16 PM
The initial problem statement could have been a little more clear, but the
diagram shows that the circle is meant to be tangent to the axis of the
ellipse. I think I always assume the diagram is right when the numbers
don't seem to be consistent with the diagram. The problem isn't actually
fundamentally different if you move the ellipse to some other location---it
just becomes a bit more complicated because the circle's y position is not
equal to the radius any more. The derivation remains the same. My
instinct is that it's easier to always place the ellipse at the origin.
You can translate the solution later if required.
I already solved this problem and posted the solution in OpenSCAD code to
this very thread, so it's not impossible. I can send it to you again if
you don't see it. I briefly outlined my solution method, which actually
involves only one equation, since there is really only one unknown, namely
the X coordinate of the circle center. Your method of intersecting the
offset curves is a nice general numerical method.
On Sat, Nov 1, 2025 at 12:49 PM Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
In the initial posting I could not find any such requirement.
The picture shown and the description is a little different it seems and
might have caused this confusion.
Description says the ellipse center is at [12,6] whereas the center of the
ellipse in the picture appears to be at the origin.
This would be very tedious to solve
there would be 2 equations here to solve for this intersection:
(x-a)^2+(y-1)^2=1 --> eq1
(x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
once the intersection point is calculated, rest is simpler
Manually maybe impossible. Need to see if this could be solved through
computer.
but in that case easier solution would be:
draw an offset to ellipse
draw a horizontal line at y=1
find intersection between the two and that is the center point
as per my calculation for this case it is : [-6.28385, 1. ]
[image: Screenshot 2025-11-01 at 10.02.47 PM.png]
The initial problem statement could have been a little more clear, but the
diagram shows that the circle is meant to be tangent to the axis of the
ellipse. I think I always assume the diagram is right when the numbers
don't seem to be consistent with the diagram. The problem isn't actually
fundamentally different if you move the ellipse to some other location---it
just becomes a bit more complicated because the circle's y position is not
equal to the radius any more. The derivation remains the same. My
instinct is that it's easier to always place the ellipse at the origin.
You can translate the solution later if required.
I already solved this problem and posted the solution in OpenSCAD code to
this very thread, so it's not impossible. I can send it to you again if
you don't see it. I briefly outlined my solution method, which actually
involves only one equation, since there is really only one unknown, namely
the X coordinate of the circle center. Your method of intersecting the
offset curves is a nice general numerical method.
On Sat, Nov 1, 2025 at 12:49 PM Sanjeev Prabhakar <sprabhakar2006@gmail.com>
wrote:
> In the initial posting I could not find any such requirement.
> The picture shown and the description is a little different it seems and
> might have caused this confusion.
> Description says the ellipse center is at [12,6] whereas the center of the
> ellipse in the picture appears to be at the origin.
>
> This would be very tedious to solve
> there would be 2 equations here to solve for this intersection:
> (x-a)^2+(y-1)^2=1 --> eq1
> (x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
> once the intersection point is calculated, rest is simpler
> Manually maybe impossible. Need to see if this could be solved through
> computer.
> but in that case easier solution would be:
> draw an offset to ellipse
> draw a horizontal line at y=1
> find intersection between the two and that is the center point
> as per my calculation for this case it is : [-6.28385, 1. ]
>
>
>
> [image: Screenshot 2025-11-01 at 10.02.47 PM.png]
>

SP
Sanjeev Prabhakar
Sat, Nov 1, 2025 6:22 PM
I understand the mistake now,
there has to be a 3rd equation which needs to be added
(x-a)^2+(y-1)^2=1 --> eq1
(x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
m1=202/92*(y-6)/(x-12) # m1 is line perpendicular to the tangent line
at intersection
v1=[1,m1] # slope converted to vector
u1=[1/(1+m1**2)0.5,m1/(1+m12)**0.5] # converted to unit vector
y-u1[1]=1 --> eq3
solving these 3 equations through computer, gives following result
intersection point : [-5.64661083533484, 1.76432791397702]
center point of unit circle: [-6.291438595217688, 0.999999999999996]
On Sat, 1 Nov 2025 at 22:46, Adrian Mariano avm4@cornell.edu wrote:
The initial problem statement could have been a little more clear, but the
diagram shows that the circle is meant to be tangent to the axis of the
ellipse. I think I always assume the diagram is right when the numbers
don't seem to be consistent with the diagram. The problem isn't actually
fundamentally different if you move the ellipse to some other location---it
just becomes a bit more complicated because the circle's y position is not
equal to the radius any more. The derivation remains the same. My
instinct is that it's easier to always place the ellipse at the origin.
You can translate the solution later if required.
I already solved this problem and posted the solution in OpenSCAD code to
this very thread, so it's not impossible. I can send it to you again if
you don't see it. I briefly outlined my solution method, which actually
involves only one equation, since there is really only one unknown, namely
the X coordinate of the circle center. Your method of intersecting the
offset curves is a nice general numerical method.
On Sat, Nov 1, 2025 at 12:49 PM Sanjeev Prabhakar <
sprabhakar2006@gmail.com> wrote:
In the initial posting I could not find any such requirement.
The picture shown and the description is a little different it seems and
might have caused this confusion.
Description says the ellipse center is at [12,6] whereas the center of
the ellipse in the picture appears to be at the origin.
This would be very tedious to solve
there would be 2 equations here to solve for this intersection:
(x-a)^2+(y-1)^2=1 --> eq1
(x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
once the intersection point is calculated, rest is simpler
Manually maybe impossible. Need to see if this could be solved through
computer.
but in that case easier solution would be:
draw an offset to ellipse
draw a horizontal line at y=1
find intersection between the two and that is the center point
as per my calculation for this case it is : [-6.28385, 1. ]
[image: Screenshot 2025-11-01 at 10.02.47 PM.png]
I understand the mistake now,
there has to be a 3rd equation which needs to be added
(x-a)^2+(y-1)^2=1 --> eq1
(x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
m1=20**2/9**2*(y-6)/(x-12) # m1 is line perpendicular to the tangent line
at intersection
v1=[1,m1] # slope converted to vector
u1=[1/(1+m1**2)**0.5,m1/(1+m1**2)**0.5] # converted to unit vector
y-u1[1]=1 --> eq3
solving these 3 equations through computer, gives following result
intersection point : [-5.64661083533484, 1.76432791397702]
center point of unit circle: [-6.291438595217688, 0.999999999999996]
On Sat, 1 Nov 2025 at 22:46, Adrian Mariano <avm4@cornell.edu> wrote:
> The initial problem statement could have been a little more clear, but the
> diagram shows that the circle is meant to be tangent to the axis of the
> ellipse. I think I always assume the diagram is right when the numbers
> don't seem to be consistent with the diagram. The problem isn't actually
> fundamentally different if you move the ellipse to some other location---it
> just becomes a bit more complicated because the circle's y position is not
> equal to the radius any more. The derivation remains the same. My
> instinct is that it's easier to always place the ellipse at the origin.
> You can translate the solution later if required.
>
> I already solved this problem and posted the solution in OpenSCAD code to
> this very thread, so it's not impossible. I can send it to you again if
> you don't see it. I briefly outlined my solution method, which actually
> involves only one equation, since there is really only one unknown, namely
> the X coordinate of the circle center. Your method of intersecting the
> offset curves is a nice general numerical method.
>
> On Sat, Nov 1, 2025 at 12:49 PM Sanjeev Prabhakar <
> sprabhakar2006@gmail.com> wrote:
>
>> In the initial posting I could not find any such requirement.
>> The picture shown and the description is a little different it seems and
>> might have caused this confusion.
>> Description says the ellipse center is at [12,6] whereas the center of
>> the ellipse in the picture appears to be at the origin.
>>
>> This would be very tedious to solve
>> there would be 2 equations here to solve for this intersection:
>> (x-a)^2+(y-1)^2=1 --> eq1
>> (x-12)^2/20^2+(y-6)^2/9^2=1. --> eq2
>> once the intersection point is calculated, rest is simpler
>> Manually maybe impossible. Need to see if this could be solved through
>> computer.
>> but in that case easier solution would be:
>> draw an offset to ellipse
>> draw a horizontal line at y=1
>> find intersection between the two and that is the center point
>> as per my calculation for this case it is : [-6.28385, 1. ]
>>
>>
>>
>> [image: Screenshot 2025-11-01 at 10.02.47 PM.png]
>>
>