3D five point star
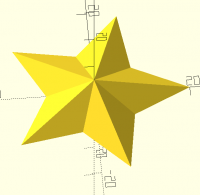
One of my projects has a star in the center. Using the “star” BOSL2 routine then linear extrude to produce a 3D object works but it looks plain, i.e. flat on top. Any suggestions how to get something like the pic below.
Thanks, Mike
The perfect solution for this would be the experimental feature roof() in OpenSCAD itself.
-Revar
On Dec 13, 2024, at 4:11 PM, mike.fraser.1945+osc--- via Discuss discuss@lists.openscad.org wrote:
One of my projects has a star in the center. Using the “star” BOSL2 routine then linear extrude to produce a 3D object works but it looks plain, i.e. flat on top. Any suggestions how to get something like the pic below.
Thanks, Mike
<embed0>OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Try:
roof(method="straight") polygon([for(i=[0:9]) let(r = i % 2 == 0 ? 50 :
20, j=sin(i36) * r, k=cos(i36) * r) [j,k]]);
On 2024-12-13 4:11 p.m., mike.fraser.1945+osc--- via Discuss wrote:
One of my projects has a star in the center. Using the “star” BOSL2
routine then linear extrude to produce a 3D object works but it looks
plain, i.e. flat on top. Any suggestions how to get something like the
pic below.
Thanks, Mike
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
Perhaps something like this:
R = 10;
roof(method="straight")
polygon([for (i=[0:9]) R*(1-(i%2)0.6)[cos(i36),sin(i36)]]);
On Fri, Dec 13, 2024 at 7:11 PM mike.fraser.1945+osc--- via Discuss <
discuss@lists.openscad.org> wrote:
One of my projects has a star in the center. Using the “star” BOSL2
routine then linear extrude to produce a 3D object works but it looks
plain, i.e. flat on top. Any suggestions how to get something like the pic
below.
Thanks, Mike
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
n = 5;
for(a = [0:n-1])
rotate([0,90,360/n*a])
scale([0.5, 1, 1])
rotate(45)
linear_extrude(40, scale = 0)
square(20, center = true);
Could do:
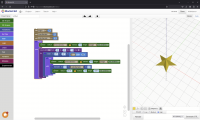
include<BOSL2/std.scad>
skin([star(n=5, or=20, ir=10), repeat([0,0],10)], z=[0,5], slices=0);
which produces:
[image: image.png]
On Fri, Dec 13, 2024 at 7:11 PM mike.fraser.1945+osc--- via Discuss <
discuss@lists.openscad.org> wrote:
One of my projects has a star in the center. Using the “star” BOSL2
routine then linear extrude to produce a 3D object works but it looks
plain, i.e. flat on top. Any suggestions how to get something like the pic
below.
Thanks, Mike
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Because I get a twisted satisfaction out of building polyhedra...
module star3d(n=5, h=2, ir=5, or=10) {
assert(n > 1, "unreasonable number of points");
// Degrees between successive points.
astep = 360/n;
// Construct a list of all of the vertexes in the polyhedron.
points = [
// The one at the peak.
[0,0,h],
// For each star point, we have that and the following "anti-point".
// Really, the only difference between or and ir is that or
// is usually larger than ir. You'll get the same figure, rotated,
// if you reverse them.
for (i=[1:n]) each [
let(a = astepi) or * [cos(a), sin(a)],
let(a = astep(i + 0.5)) ir * [cos(a), sin(a)],
]
];
// The trickier part of building a polyhedron is usually
// constructing the lists of points in the faces.
faces = [
// The star-shaped face on the bottom.
[ for (i=[1:2n]) i ],
// For each star point and anti-point, connect the
// point to the center, and thence to the next
// point, wrapping around at the end.
// Remember that our star points and anti-points have indexes
// 1..2n.
for (i=[1:2n]) [
i, 0, i%(2n)+1
]
];
polyhedron(points=points, faces=faces);
}
// A couple of examples.
star3d();
translate([20,0,0]) star3d(n=7, ir=2, h=4);
translate([40,0,0]) star3d(n=3, ir=4);
translate([60,0,0]) star3d(n=2, ir=4);
Here is another approach:
//!OpenSCAD
height = 5;
innerdiameter = 5;
outerdiameter = 15;
union(){
cylinder(r1=innerdiameter, r2=0, h=height, center=false);
for (i = [0 : abs(1) : 5]) {
rotate([0, 0, (i * 72)]){
hull(){
cylinder(r1=innerdiameter, r2=0, h=height, center=false);
translate([0, outerdiameter, 0]){
cylinder(r1=0.01, r2=0, h=0.01, center=false);
}
}
}
}
}
Added a variable, so now the number of points is variable:
You have got already complete solution without extra libraries,
but just in case https://www.thingiverse.com/thing:3428265 :-)
From: mike.fraser.1945+osc--- via Discuss discuss@lists.openscad.org
Sent: 14 December 2024 02:11:05
To: discuss@lists.openscad.org
Cc: mike.fraser.1945+osc@gmail.com
Subject: [OpenSCAD] 3D five point star
One of my projects has a star in the center. Using the “star” BOSL2 routine then linear extrude to produce a 3D object works but it looks plain, i.e. flat on top. Any suggestions how to get something like the pic below.
Thanks, Mike