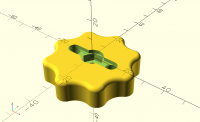
Problems with not closed mesh / minkowski - may be platform related (AppleSilicon)
Sorry for possible double postings. I already sent this a couple of hours ago but it never showed up in the mailing list. Is there some acknowledgement process performed by the list admins? I didn't find any resources about the do's and don'ts on this list.
My question:
I am creating simple knobs for hexagonal head screws (see simplified code below). The preview works but when rendering I get this error:
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
Until now I only saw this when importing broken stl files but never with calculated geometries. The error vanishes if I remove the last element of the difference, marked with the comment "cut off excessive height from minkowski operator".
Even more strange: Yesterday it used to work with an edgeRadius of 2.02 instead of 2 but after a few slight changes it doesn't do anymore. With radius 2 it never worked.
I would appreciate if someone could test this and let me know if this appears to just be a platform related problem caused by cumulating floating point errors. I am using a Macbook with M3 cpu.
Handle with care: rendering time is about 5 minutes.
Bonus question: is there a way to achieve the same geometry (rounded edge) without using the minkowski operator?
Best regards, Thomas
// Diameter of the screw head, largest dimension, NOT the wrench size.
// In DIN and ISO dimension tables, this dimension is usually designated as e.
// ___
// /
// ___/
// --e--
// M5 screw
screwHeadDiameter = 9.2;
// In DIN and ISO dimension tables, this dimension is usually designated as k.
screwHeadHeight = 3.5;
// Size of the screw (M4, M5, ...). In DIN and ISO dimension tables, this dimension is usually designated as d1.
screwDiameter = 5;
// size of the knob, can alternatively be set to a constant value
knobDiameter = screwDiameter * 8;
// Length of the screw shank that should be inside the knob,
// can alternatively be set to a constant value
protrusion = screwDiameter - 1;
// perimeter thickness above the screw head
headPerimeter = 2;
knobHeight = headPerimeter + screwHeadHeight + protrusion;
// number of knurls around the circumference
knurls = 8;
// pitch of the knurls: a pitch of one means that one knurl radius ist between two knurls, a pitch of two means that two knurl radii are between two knurls. Since the circumference is constant this setting controls the radius of the knurls: the larger the pitch, the smaller the knurls. Sensible Values are 1, 2, 3
knurlPitch = 2;
// ratio of knurl diameter to notch diameter
// 2 means, notches have twice the radius of knurls.
// The higher the notchRatio is, the flatter the notches are. Sensible values are between 2 and 5
notchRatio = 4;
// radius of the rounded edge. set to 0 for faster calculation when testing
edgeRadius = 2;
// The higher the better the quality, the higher the computing time
// choose 12 or lower for testing.
EDGE_QUALITY = 36;
eD = edgeRadius * 2;
f = (knobDiameter - eD) / knobDiameter;
rotate([180, 0, 0])
difference() {
translate([0, 0, edgeRadius]) {
minkowski(10) {
sphere(edgeRadius, $fn = EDGE_QUALITY);
scale([f, f, 1]) {
angleStep = 360 / knurls;
// radius of the knob
rKnob = knobDiameter / 2;
// rKnobdius of the knurls
rK = PI * rKnob / ((knurlPitch + 1) * knurls + PI);
// radius of the notches
rN = notchRatio * rK;
// radius of the circle to place the knurls
rPosK = rKnob - rK;
// angle between knurl and notch
alpha = angleStep / 2;
// angle between center of knob, center of notch, center of knurl
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of knurl, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches
rPosN = rPosK * sin(beta) / sin(gamma);
// radius of the knob's core: distance from center to touch point between knurl and notch
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
difference() {
union() {
cylinder(h = knobHeight, d = rCore * 2, $fn = 72);
for (i = [0: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosK, 0, 0]) { cylinder(h = knobHeight, d = rK * 2, $fn = 72); }
}
}
}
for (i = [alpha: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosN, 0, 0]) { cylinder(h = knobHeight, d = rN * 2, $fn = 72); }
}
}
}
}
}
}
// cut off excessive height from minkowski operator
// this seems to cause the "mesh is not closed" error
translate([0, 0, knobHeight]) {
#cylinder(h = eD, d = knobDiameter + 2);
}
}
Probably because minkowski created some geometry where there is
edge/vertex sharing, which is not really a 2-manifold in the geometric
sense, and CGAL doesn't like that.
Manifold can handle it though. Try the latest nightly and select
manifold as the rendering backend. It takes 1.5s on my machine to render
this.
On 12/14/24 05:56, Thomas Richter via Discuss wrote:
Sorry for possible double postings. I already sent this a couple of hours ago but it never showed up in the mailing list. Is there some acknowledgement process performed by the list admins? I didn't find any resources about the do's and don'ts on this list.
My question:
I am creating simple knobs for hexagonal head screws (see simplified code below). The preview works but when rendering I get this error:
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
Until now I only saw this when importing broken stl files but never with calculated geometries. The error vanishes if I remove the last element of the difference, marked with the comment "cut off excessive height from minkowski operator".
Even more strange: Yesterday it used to work with an edgeRadius of 2.02 instead of 2 but after a few slight changes it doesn't do anymore. With radius 2 it never worked.
I would appreciate if someone could test this and let me know if this appears to just be a platform related problem caused by cumulating floating point errors. I am using a Macbook with M3 cpu.
Handle with care: rendering time is about 5 minutes.
Bonus question: is there a way to achieve the same geometry (rounded edge) without using the minkowski operator?
Best regards, Thomas
// Diameter of the screw head, largest dimension, NOT the wrench size.
// In DIN and ISO dimension tables, this dimension is usually designated as e.
// ___
// /
// ___/
// --e--
// M5 screw
screwHeadDiameter = 9.2;
// In DIN and ISO dimension tables, this dimension is usually designated as k.
screwHeadHeight = 3.5;
// Size of the screw (M4, M5, ...). In DIN and ISO dimension tables, this dimension is usually designated as d1.
screwDiameter = 5;
// size of the knob, can alternatively be set to a constant value
knobDiameter = screwDiameter * 8;
// Length of the screw shank that should be inside the knob,
// can alternatively be set to a constant value
protrusion = screwDiameter - 1;
// perimeter thickness above the screw head
headPerimeter = 2;
knobHeight = headPerimeter + screwHeadHeight + protrusion;
// number of knurls around the circumference
knurls = 8;
// pitch of the knurls: a pitch of one means that one knurl radius ist between two knurls, a pitch of two means that two knurl radii are between two knurls. Since the circumference is constant this setting controls the radius of the knurls: the larger the pitch, the smaller the knurls. Sensible Values are 1, 2, 3
knurlPitch = 2;
// ratio of knurl diameter to notch diameter
// 2 means, notches have twice the radius of knurls.
// The higher the notchRatio is, the flatter the notches are. Sensible values are between 2 and 5
notchRatio = 4;
// radius of the rounded edge. set to 0 for faster calculation when testing
edgeRadius = 2;
// The higher the better the quality, the higher the computing time
// choose 12 or lower for testing.
EDGE_QUALITY = 36;
eD = edgeRadius * 2;
f = (knobDiameter - eD) / knobDiameter;
rotate([180, 0, 0])
difference() {
translate([0, 0, edgeRadius]) {
minkowski(10) {
sphere(edgeRadius, $fn = EDGE_QUALITY);
scale([f, f, 1]) {
angleStep = 360 / knurls;
// radius of the knob
rKnob = knobDiameter / 2;
// rKnobdius of the knurls
rK = PI * rKnob / ((knurlPitch + 1) * knurls + PI);
// radius of the notches
rN = notchRatio * rK;
// radius of the circle to place the knurls
rPosK = rKnob - rK;
// angle between knurl and notch
alpha = angleStep / 2;
// angle between center of knob, center of notch, center of knurl
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of knurl, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches
rPosN = rPosK * sin(beta) / sin(gamma);
// radius of the knob's core: distance from center to touch point between knurl and notch
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
difference() {
union() {
cylinder(h = knobHeight, d = rCore * 2, $fn = 72);
for (i = [0: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosK, 0, 0]) { cylinder(h = knobHeight, d = rK * 2, $fn = 72); }
}
}
}
for (i = [alpha: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosN, 0, 0]) { cylinder(h = knobHeight, d = rN * 2, $fn = 72); }
}
}
}
}
}
}
// cut off excessive height from minkowski operator
// this seems to cause the "mesh is not closed" error
translate([0, 0, knobHeight]) {
#cylinder(h = eD, d = knobDiameter + 2);
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I agree with Chun Kit Lam.
I'm running 2024.10.02 nightly with manifold enabled and f5 was 0.088 seconds, f6 was 0.069 seconds, both with no errors.
On 2024-12-14 08:56, Thomas Richter via Discuss wrote:
My question:
I am creating simple knobs for hexagonal head screws (see simplified code below). The preview works but when rendering I get this error:
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
--
Cheers, Ken
bats059@gmail.com
https://vk7krj.com
https://vk7krj.com/running.html
A baby can be defined as an ego with a noise at one end and a smell at the other.
Your job as parents is to teach them to control all three.
My job as a grandad is to tell you how you are doing it all wrong!
On 12/13/2024 1:56 PM, Thomas Richter via Discuss wrote:
Sorry for possible double postings. I already sent this a couple of hours ago but it never showed up in the mailing list. Is there some acknowledgement process performed by the list admins? I didn't find any resources about the do's and don'ts on this list.
It's pretty much a plain vanilla mailing list, with archiving. There is
no approval required for messages. I don't see any previous message
from you. I don't happen to remember whether you have to be a member to
post in the first place; I think you do.
Bonus question: is there a way to achieve the same geometry (rounded edge) without using the minkowski operator?
BOSL2 does quite a variety of things with rounded edges. It does all of
its work by constructing polyhedra, but unless you want to look at them
it hides the polyhedra from you.
https://github.com/BelfrySCAD/BOSL2/wiki
Knurling is used in machining, as a simple method often in a lathe work
to add a grippy surface (usually by embossing a fine pattern) to a
metal cylinder. If you are 3d printing, you can get much better methods
of getting a grip, allowing the fdm process to remove the sharp edges
that can occur in the knurling of metal components, so sharp points are OK.
So, start with the cylinder with the recess for the nut, then simply
rotate shapes to give a suitable number of ridges - very similar to the
star problem that Mike had. As you found out, Minkowski can be very
slow, and does not always work - it often 'produces too many small
triangles'
Personally, i would not use fine knurling, simply adjust num and remove
the $fn=4, and make k bigger, so that there are fewer, but larger
rounded ridges.
On 13/12/2024 21:56, Thomas Richter via Discuss wrote:
Sorry for possible double postings. I already sent this a couple of hours ago but it never showed up in the mailing list. Is there some acknowledgement process performed by the list admins? I didn't find any resources about the do's and don'ts on this list.
My question:
I am creating simple knobs for hexagonal head screws (see simplified code below). The preview works but when rendering I get this error:
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
Until now I only saw this when importing broken stl files but never with calculated geometries. The error vanishes if I remove the last element of the difference, marked with the comment "cut off excessive height from minkowski operator".
Even more strange: Yesterday it used to work with an edgeRadius of 2.02 instead of 2 but after a few slight changes it doesn't do anymore. With radius 2 it never worked.
I would appreciate if someone could test this and let me know if this appears to just be a platform related problem caused by cumulating floating point errors. I am using a Macbook with M3 cpu.
Handle with care: rendering time is about 5 minutes.
Bonus question: is there a way to achieve the same geometry (rounded edge) without using the minkowski operator?
Best regards, Thomas
// Diameter of the screw head, largest dimension, NOT the wrench size.
// In DIN and ISO dimension tables, this dimension is usually designated as e.
// ___
// /
// ___/
// --e--
// M5 screw
screwHeadDiameter = 9.2;
// In DIN and ISO dimension tables, this dimension is usually designated as k.
screwHeadHeight = 3.5;
// Size of the screw (M4, M5, ...). In DIN and ISO dimension tables, this dimension is usually designated as d1.
screwDiameter = 5;
// size of the knob, can alternatively be set to a constant value
knobDiameter = screwDiameter * 8;
// Length of the screw shank that should be inside the knob,
// can alternatively be set to a constant value
protrusion = screwDiameter - 1;
// perimeter thickness above the screw head
headPerimeter = 2;
knobHeight = headPerimeter + screwHeadHeight + protrusion;
// number of knurls around the circumference
knurls = 8;
// pitch of the knurls: a pitch of one means that one knurl radius ist between two knurls, a pitch of two means that two knurl radii are between two knurls. Since the circumference is constant this setting controls the radius of the knurls: the larger the pitch, the smaller the knurls. Sensible Values are 1, 2, 3
knurlPitch = 2;
// ratio of knurl diameter to notch diameter
// 2 means, notches have twice the radius of knurls.
// The higher the notchRatio is, the flatter the notches are. Sensible values are between 2 and 5
notchRatio = 4;
// radius of the rounded edge. set to 0 for faster calculation when testing
edgeRadius = 2;
// The higher the better the quality, the higher the computing time
// choose 12 or lower for testing.
EDGE_QUALITY = 36;
eD = edgeRadius * 2;
f = (knobDiameter - eD) / knobDiameter;
rotate([180, 0, 0])
difference() {
translate([0, 0, edgeRadius]) {
minkowski(10) {
sphere(edgeRadius, $fn = EDGE_QUALITY);
scale([f, f, 1]) {
angleStep = 360 / knurls;
// radius of the knob
rKnob = knobDiameter / 2;
// rKnobdius of the knurls
rK = PI * rKnob / ((knurlPitch + 1) * knurls + PI);
// radius of the notches
rN = notchRatio * rK;
// radius of the circle to place the knurls
rPosK = rKnob - rK;
// angle between knurl and notch
alpha = angleStep / 2;
// angle between center of knob, center of notch, center of knurl
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of knurl, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches
rPosN = rPosK * sin(beta) / sin(gamma);
// radius of the knob's core: distance from center to touch point between knurl and notch
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
difference() {
union() {
cylinder(h = knobHeight, d = rCore * 2, $fn = 72);
for (i = [0: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosK, 0, 0]) { cylinder(h = knobHeight, d = rK * 2, $fn = 72); }
}
}
}
for (i = [alpha: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosN, 0, 0]) { cylinder(h = knobHeight, d = rN * 2, $fn = 72); }
}
}
}
}
}
}
// cut off excessive height from minkowski operator
// this seems to cause the "mesh is not closed" error
translate([0, 0, knobHeight]) {
#cylinder(h = eD, d = knobDiameter + 2);
}
}
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
Am 14.12.2024 um 13:13 schrieb Raymond West via Discuss discuss@lists.openscad.org:
Knurling is used in machining, as a simple method often in a lathe wose to add a grippy surface (usually by embossing a fine pattern) to a metal cylinder. If you are 3d printing, you can get much better methods of getting a grip, allowing the fdm process to remove the sharp edges that can occur in the knurling of metal components, so sharp points are OK.
Thank you for your insights. I know about the origins of knurling, I just didn't find a better word for my case (not an english native speaker). In this project I want to create grips for hex screws that can be operated by hand like, e. g., tightening screws for T-nut-slots.
So, start with the cylinder with the recess for the nut, then simply rotate shapes to give a suitable number of ridges - very similar to the star problem that Mike had. As you found out, Minkowski can be very slow, and does not always work - it often 'produces too many small triangles'
<knurl.jpg>Personally, i would not use fine knurling, simply adjust num and remove the $fn=4, and make k bigger, so that there are fewer, but larger rounded ridges.
My first solution was very basic with recesses like you recommend. But then I was somewhat pulled into this starting to make a multi-purpose library. The example I posted here was just a very simplified, focused on the problem, variant of the actual implementation. I came up with cylinders of different radii touching each other to make a smooth perimeter along the circumference. Many things can be configured and I went through several refactorings until I ran into the problem posted here. With the manifold backend recommended by Chun Kit Lam and Ken everything works like a charm and considerably faster as well.
On 13/12/2024 21:56, Thomas Richter via Discuss wrote:
Sorry for possible double postings. I already sent this a couple of hours ago but it never showed up in the mailing list. Is there some acknowledgement process performed by the list admins? I didn't find any resources about the do's and don'ts on this list.
My question:
I am creating simple knobs for hexagonal head screws (see simplified code below). The preview works but when rendering I get this error:
ERROR: The given mesh is not closed! Unable to convert to CGAL_Nef_Polyhedron.
Until now I only saw this when importing broken stl files but never with calculated geometries. The error vanishes if I remove the last element of the difference, marked with the comment "cut off excessive height from minkowski operator".
Even more strange: Yesterday it used to work with an edgeRadius of 2.02 instead of 2 but after a few slight changes it doesn't do anymore. With radius 2 it never worked.
I would appreciate if someone could test this and let me know if this appears to just be a platform related problem caused by cumulating floating point errors. I am using a Macbook with M3 cpu.
Handle with care: rendering time is about 5 minutes.
Bonus question: is there a way to achieve the same geometry (rounded edge) without using the minkowski operator?
Best regards, Thomas
// Diameter of the screw head, largest dimension, NOT the wrench size.
// In DIN and ISO dimension tables, this dimension is usually designated as e.
// ___
// /
// ___/
// --e--
// M5 screw
screwHeadDiameter = 9.2;
// In DIN and ISO dimension tables, this dimension is usually designated as k.
screwHeadHeight = 3.5;
// Size of the screw (M4, M5, ...). In DIN and ISO dimension tables, this dimension is usually designated as d1.
screwDiameter = 5;
// size of the knob, can alternatively be set to a constant value
knobDiameter = screwDiameter * 8;
// Length of the screw shank that should be inside the knob,
// can alternatively be set to a constant value
protrusion = screwDiameter - 1;
// perimeter thickness above the screw head
headPerimeter = 2;
knobHeight = headPerimeter + screwHeadHeight + protrusion;
// number of knurls around the circumference
knurls = 8;
// pitch of the knurls: a pitch of one means that one knurl radius ist between two knurls, a pitch of two means that two knurl radii are between two knurls. Since the circumference is constant this setting controls the radius of the knurls: the larger the pitch, the smaller the knurls. Sensible Values are 1, 2, 3
knurlPitch = 2;
// ratio of knurl diameter to notch diameter
// 2 means, notches have twice the radius of knurls.
// The higher the notchRatio is, the flatter the notches are. Sensible values are between 2 and 5
notchRatio = 4;
// radius of the rounded edge. set to 0 for faster calculation when testing
edgeRadius = 2;
// The higher the better the quality, the higher the computing time
// choose 12 or lower for testing.
EDGE_QUALITY = 36;
eD = edgeRadius * 2;
f = (knobDiameter - eD) / knobDiameter;
rotate([180, 0, 0])
difference() {
translate([0, 0, edgeRadius]) {
minkowski(10) {
sphere(edgeRadius, $fn = EDGE_QUALITY);
scale([f, f, 1]) {
angleStep = 360 / knurls;
// radius of the knob
rKnob = knobDiameter / 2;
// rKnobdius of the knurls
rK = PI * rKnob / ((knurlPitch + 1) * knurls + PI);
// radius of the notches
rN = notchRatio * rK;
// radius of the circle to place the knurls
rPosK = rKnob - rK;
// angle between knurl and notch
alpha = angleStep / 2;
// angle between center of knob, center of notch, center of knurl
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of knurl, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches
rPosN = rPosK * sin(beta) / sin(gamma);
// radius of the knob's core: distance from center to touch point between knurl and notch
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
difference() {
union() {
cylinder(h = knobHeight, d = rCore * 2, $fn = 72);
for (i = [0: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosK, 0, 0]) { cylinder(h = knobHeight, d = rK * 2, $fn = 72); }
}
}
}
for (i = [alpha: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosN, 0, 0]) { cylinder(h = knobHeight, d = rN * 2, $fn = 72); }
}
}
}
}
}
}
// cut off excessive height from minkowski operator
// this seems to cause the "mesh is not closed" error
translate([0, 0, knobHeight]) {
#cylinder(h = eD, d = knobDiameter + 2);
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I don't know about the idea that you can just make it sharp. My daughter
3d printed hedgehogs with tetrahedral spines and those suckers are SHARP.
Very uncomfortable to hold without care.
If you want more knurling options, you might find BOSL2 textures of
interest:
https://github.com/BelfrySCAD/BOSL2/wiki/skin.scad#function-texture
You can use the textures with the BOSL2 module cyl() which is an extension
of the standard cylinder().
On Sat, Dec 14, 2024 at 8:28 AM Thomas Richter via Discuss <
discuss@lists.openscad.org> wrote:
Am 14.12.2024 um 13:13 schrieb Raymond West via Discuss <
Knurling is used in machining, as a simple method often in a lathe wose
to add a grippy surface (usually by embossing a fine pattern) to a metal
cylinder. If you are 3d printing, you can get much better methods of
getting a grip, allowing the fdm process to remove the sharp edges that can
occur in the knurling of metal components, so sharp points are OK.
Thank you for your insights. I know about the origins of knurling, I just
didn't find a better word for my case (not an english native speaker). In
this project I want to create grips for hex screws that can be operated by
hand like, e. g., tightening screws for T-nut-slots.
So, start with the cylinder with the recess for the nut, then simply
rotate shapes to give a suitable number of ridges - very similar to the
star problem that Mike had. As you found out, Minkowski can be very slow,
and does not always work - it often 'produces too many small triangles'
<knurl.jpg>Personally, i would not use fine knurling, simply adjust num
and remove the $fn=4, and make k bigger, so that there are fewer, but
larger rounded ridges.
My first solution was very basic with recesses like you recommend. But
then I was somewhat pulled into this starting to make a multi-purpose
library. The example I posted here was just a very simplified, focused on
the problem, variant of the actual implementation. I came up with cylinders
of different radii touching each other to make a smooth perimeter along the
circumference. Many things can be configured and I went through several
refactorings until I ran into the problem posted here. With the manifold
backend recommended by Chun Kit Lam and Ken everything works like a charm
and considerably faster as well.
On 13/12/2024 21:56, Thomas Richter via Discuss wrote:
Sorry for possible double postings. I already sent this a couple of
hours ago but it never showed up in the mailing list. Is there some
acknowledgement process performed by the list admins? I didn't find any
resources about the do's and don'ts on this list.
My question:
I am creating simple knobs for hexagonal head screws (see simplified
code below). The preview works but when rendering I get this error:
ERROR: The given mesh is not closed! Unable to convert to
CGAL_Nef_Polyhedron.
Until now I only saw this when importing broken stl files but never
with calculated geometries. The error vanishes if I remove the last element
of the difference, marked with the comment "cut off excessive height from
minkowski operator".
Even more strange: Yesterday it used to work with an edgeRadius of 2.02
instead of 2 but after a few slight changes it doesn't do anymore. With
radius 2 it never worked.
I would appreciate if someone could test this and let me know if this
appears to just be a platform related problem caused by cumulating floating
point errors. I am using a Macbook with M3 cpu.
Handle with care: rendering time is about 5 minutes.
Bonus question: is there a way to achieve the same geometry (rounded
edge) without using the minkowski operator?
Best regards, Thomas
// Diameter of the screw head, largest dimension, NOT the wrench size.
// In DIN and ISO dimension tables, this dimension is usually
designated as e.
// ___
// /
// ___/
// --e--
// M5 screw
screwHeadDiameter = 9.2;
// In DIN and ISO dimension tables, this dimension is usually
designated as k.
screwHeadHeight = 3.5;
// Size of the screw (M4, M5, ...). In DIN and ISO dimension tables,
this dimension is usually designated as d1.
screwDiameter = 5;
// size of the knob, can alternatively be set to a constant value
knobDiameter = screwDiameter * 8;
// Length of the screw shank that should be inside the knob,
// can alternatively be set to a constant value
protrusion = screwDiameter - 1;
// perimeter thickness above the screw head
headPerimeter = 2;
knobHeight = headPerimeter + screwHeadHeight + protrusion;
// number of knurls around the circumference
knurls = 8;
// pitch of the knurls: a pitch of one means that one knurl radius ist
between two knurls, a pitch of two means that two knurl radii are between
two knurls. Since the circumference is constant this setting controls the
radius of the knurls: the larger the pitch, the smaller the knurls.
Sensible Values are 1, 2, 3
knurlPitch = 2;
// ratio of knurl diameter to notch diameter
// 2 means, notches have twice the radius of knurls.
// The higher the notchRatio is, the flatter the notches are. Sensible
values are between 2 and 5
notchRatio = 4;
// radius of the rounded edge. set to 0 for faster calculation when
testing
edgeRadius = 2;
// The higher the better the quality, the higher the computing time
// choose 12 or lower for testing.
EDGE_QUALITY = 36;
eD = edgeRadius * 2;
f = (knobDiameter - eD) / knobDiameter;
rotate([180, 0, 0])
difference() {
translate([0, 0, edgeRadius]) {
minkowski(10) {
sphere(edgeRadius, $fn = EDGE_QUALITY);
scale([f, f, 1]) {
angleStep = 360 / knurls;
// radius of the knob
rKnob = knobDiameter / 2;
// rKnobdius of the knurls
rK = PI * rKnob / ((knurlPitch + 1) * knurls + PI);
// radius of the notches
rN = notchRatio * rK;
// radius of the circle to place the knurls
rPosK = rKnob - rK;
// angle between knurl and notch
alpha = angleStep / 2;
// angle between center of knob, center of notch, center of knurl
gamma = asin(sin(alpha) * rPosK / (rN + rK));
// angle between center of knob, center of knurl, center of notch
beta = 180 - alpha - gamma;
// radius of the circle to place the notches
rPosN = rPosK * sin(beta) / sin(gamma);
// radius of the knob's core: distance from center to touch point
between knurl and notch
rCore = sqrt(rPosK^2 + rK^2 - 2 * rPosK * rK * cos(beta));
difference() {
union() {
cylinder(h = knobHeight, d = rCore * 2, $fn = 72);
for (i = [0: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosK, 0, 0]) { cylinder(h = knobHeight, d = rK * 2, $fn =
72); }
}
}
}
for (i = [alpha: angleStep: 360]) {
rotate([0, 0, i]) {
translate([rPosN, 0, 0]) { cylinder(h = knobHeight, d = rN * 2, $fn =
72); }
}
}
}
}
}
}
// cut off excessive height from minkowski operator
// this seems to cause the "mesh is not closed" error
translate([0, 0, knobHeight]) {
#cylinder(h = eD, d = knobDiameter + 2);
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Thanks to the help of all of you, I came up with this (dosen't look that sharp). Number and size of knurls and notches can be configured as well as height, diameter, screw head size. Future versions of the library will feature a rounded top, bottom spacers, and a release mechanism to let the knob turn freely while the screw remains tightened.
Am 14.12.2024 um 15:16 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I don't know about the idea that you can just make it sharp. My daughter 3d printed hedgehogs with tetrahedral spines and those suckers are SHARP. Very uncomfortable to hold without care.
If you want more knurling options, you might find BOSL2 textures of interest:
https://github.com/BelfrySCAD/BOSL2/wiki/skin.scad#function-texture
You can use the textures with the BOSL2 module cyl() which is an extension of the standard cylinder().
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On 14/12/2024 14:16, Adrian Mariano via Discuss wrote:
I don't know about the idea that you can just make it sharp.
I was referring to knurling, not daggers... Often folk do not get
knurling correct in metal work, leaving sharp peaks on the surface of
the ridges. The nature of 3d fdm printing is that you are unlikely to
get a point sharper than the radius of the nozzle, using a normal
slicer. You can see that in the image below (a much enlarged section
from the 20mm diameter piece from before, you can possibly see the light
grey of the original stl points at the base)..
If the sharp points on the hedgehogs are a nuisance, then print in a
flexible (tpu) filament, or quickly go over it with a heat gun/blow
torch/whatever, or print in abs and 'polish' using acetone - other safer
solvents are available for this and some other plastics.
I guess it is what could be referred to as a 'scalloped' hand-wheel. I
see you are also venturing into feature creep. Welcome to the rabbit
holes. Is 'release mechanism' a fancy name for 'layer separation'?
On 14/12/2024 15:13, Thomas Richter via Discuss wrote:
Thanks to the help of all of you, I came up with this (dosen't look that sharp). Number and size of knurls and notches can be configured as well as height, diameter, screw head size. Future versions of the library will feature a rounded top, bottom spacers, and a release mechanism to let the knob turn freely while the screw remains tightened.
Am 14.12.2024 um 15:16 schrieb Adrian Mariano via Discuss discuss@lists.openscad.org:
I don't know about the idea that you can just make it sharp. My daughter 3d printed hedgehogs with tetrahedral spines and those suckers are SHARP. Very uncomfortable to hold without care.
If you want more knurling options, you might find BOSL2 textures of interest:
https://github.com/BelfrySCAD/BOSL2/wiki/skin.scad#function-texture
You can use the textures with the BOSL2 module cyl() which is an extension of the standard cylinder().
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org