
BB
Bruno Boettcher
Thu, May 26, 2022 9:04 PM
Hello!
i want to draw a caduceus for my wife.... so i need some spiraling snake....
using directly linear_extrude as in the cheatsheet works nice, but i wanted
to give the snakes some shape....
is there a way to know in the children of the linear_extrude the actual
height?
i would like to do something like this:
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
linear_extrude(height = l, center = false, convexity = 10, twist =
turns*360)
translate([schlrad(d=d,l=l,y=magical_height_here), 0, 0])
circle(r = 1);
}
ATM the polygons of the sections are the same for each layer, thus i could
also use some sort of sweep library, but this would make the whole a little
more complex....
but if i also add some scales on the snakes, soon, the polygons between
slices will be different...
and the sweep construction even harder to achieve....
so easiest would be to have access to the actual height in the
linear_extrude... some way to get it?
--
ciao
Bruno
---==========
http://nohkumado.eu/, http://bboett.free.frhttp://aikido.nohkumado.eu/,
http://bboett.free.fr
http://aikido.zorn.free.fr
Hello!
i want to draw a caduceus for my wife.... so i need some spiraling snake....
using directly linear_extrude as in the cheatsheet works nice, but i wanted
to give the snakes some shape....
is there a way to know in the children of the linear_extrude the actual
height?
i would like to do something like this:
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
linear_extrude(height = l, center = false, convexity = 10, twist =
turns*360)
translate([schlrad(d=d,l=l,y=magical_height_here), 0, 0])
circle(r = 1);
}
ATM the polygons of the sections are the same for each layer, thus i could
also use some sort of sweep library, but this would make the whole a little
more complex....
but if i also add some scales on the snakes, soon, the polygons between
slices will be different...
and the sweep construction even harder to achieve....
so easiest would be to have access to the actual height in the
linear_extrude... some way to get it?
--
ciao
Bruno
===========================================
http://nohkumado.eu/, <http://bboett.free.fr>http://aikido.nohkumado.eu/,
<http://bboett.free.fr>
http://aikido.zorn.free.fr

TP
Torsten Paul
Thu, May 26, 2022 11:11 PM
On 26.05.22 23:04, Bruno Boettcher wrote:
is there a way to know in the children of the linear_extrude
the actual height? i would like to do something like this:
No, that is fundamentally not possible as the evaluation order is
from bottom to top of the CSG tree.
The way to potentially implement this kind of feature would be
passing the function as parameter to linear_extrude(). The
framework for that exists now, but nobody has actually tried
this yet.
An alternative suggestion that seems to have stalled unfortunately
can be found in https://github.com/openscad/openscad/pull/2796
ciao,
Torsten.
On 26.05.22 23:04, Bruno Boettcher wrote:
> is there a way to know in the children of the linear_extrude
> the actual height? i would like to do something like this:
No, that is fundamentally not possible as the evaluation order is
from bottom to top of the CSG tree.
The way to potentially implement this kind of feature would be
passing the function as parameter to linear_extrude(). The
framework for that exists now, but nobody has actually tried
this yet.
An alternative suggestion that seems to have stalled unfortunately
can be found in https://github.com/openscad/openscad/pull/2796
ciao,
Torsten.

JB
Jordan Brown
Fri, May 27, 2022 1:21 AM
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
However, I expect that that would yield a whole different set of
problems: how would you connect the vertices from one step to the
next? If one step yielded a triangle and the next pentagon, what would
be the right way to connect the vertices? And of course that would only
get more complex as the complexity of the figure grew.
I'm not saying it can't be done, only that it's not obvious how ti would
work.
Another alternative is to build your own polyhedron. That's tedious,
but not really that hard once you get the pattern down. Here's a DIY
implementation of linear extrude that you could work from. Let me know
if a line-by-line walkthrough would be helpful. (I'm happy to do it,
but it's a lot of typing if you don't need it.)
I originally wrote this as a demonstration of the difference between
linear_extrude's current behavior (twist and then scale) and what I
thought would be a better behavior (scale and then twist).
The basic idea is to build up a list of all of the points, one layer at
a time, and then a list of all of the faces, starting with the bottom,
then for each layer all of the "downward pointing" triangles, then for
each layer all of the "upward pointing" triangles, then the top.
linear_extrude(height=5, twist=45, scale=[5,1], slices=20) square(1, center=true);
points = [[-0.5,-0.5], [0.5,-0.5], [0.5, 0.5], [-0.5, 0.5]];
translate([7,0,0]) lx(points=points, h=5, twist=45, scale=[5,1], slices=10);
// --- Following is a DIY implementation of linear_extrude that scales and then twists.
function rot(points, a) = [
for (p = points) [p.xcos(a)-p.ysin(a), p.xsin(a)+p.ycos(a)]
];
function scale2(points, scale) =
let(scale = is_list(scale) ? scale : [scale, scale])
[ for (p = points) [p.x * scale.x, p.y*scale.y] ];
module lx(points, twist=0, scale=1, h, slices, convexity=5) {
slices = is_undef(slices) ? h : slices;
points3 = [
for (i = [0:slices])
let (fraction = i/slices)
let (pscale = scale2(points, [1,1]+(scale-[1,1])fraction))
let (prot = rot(pscale, fractiontwist))
let (z = ih/slices)
for (p = prot) [ p.x, p.y, z ]
];
n = len(points);
r = [0:n-1];
faces = [
[ for (pi = r) pi ],
for (zi = [0:slices-1])
let(base = zin)
for (pi = r) [ base+pi, base+n+pi, base+n+(pi+1)%n ],
for (zi = [0:slices-1])
let(base = zin)
for (pi = r) [ base+pi, base+n+(pi+1)%n, base+(pi+1)%n ],
[ for (pi = [n-1:-1:0]) nslices+pi ]
];
polyhedron(points=points3, faces=faces, convexity=convexity);
}
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
However, I expect that that would yield a whole different set of
problems: how would you connect the vertices from one step to the
next? If one step yielded a triangle and the next pentagon, what would
be the right way to connect the vertices? And of course that would only
get more complex as the complexity of the figure grew.
I'm not saying it can't be done, only that it's not obvious how ti would
work.
Another alternative is to build your own polyhedron. That's tedious,
but not really that hard once you get the pattern down. Here's a DIY
implementation of linear extrude that you could work from. Let me know
if a line-by-line walkthrough would be helpful. (I'm happy to do it,
but it's a lot of typing if you don't need it.)
I originally wrote this as a demonstration of the difference between
linear_extrude's current behavior (twist and then scale) and what I
thought would be a better behavior (scale and then twist).
The basic idea is to build up a list of all of the points, one layer at
a time, and then a list of all of the faces, starting with the bottom,
then for each layer all of the "downward pointing" triangles, then for
each layer all of the "upward pointing" triangles, then the top.
---
linear_extrude(height=5, twist=45, scale=[5,1], slices=20) square(1, center=true);
points = [[-0.5,-0.5], [0.5,-0.5], [0.5, 0.5], [-0.5, 0.5]];
translate([7,0,0]) lx(points=points, h=5, twist=45, scale=[5,1], slices=10);
// --- Following is a DIY implementation of linear_extrude that scales and *then* twists.
function rot(points, a) = [
for (p = points) [p.x*cos(a)-p.y*sin(a), p.x*sin(a)+p.y*cos(a)]
];
function scale2(points, scale) =
let(scale = is_list(scale) ? scale : [scale, scale])
[ for (p = points) [p.x * scale.x, p.y*scale.y] ];
module lx(points, twist=0, scale=1, h, slices, convexity=5) {
slices = is_undef(slices) ? h : slices;
points3 = [
for (i = [0:slices])
let (fraction = i/slices)
let (pscale = scale2(points, [1,1]+(scale-[1,1])*fraction))
let (prot = rot(pscale, fraction*twist))
let (z = i*h/slices)
for (p = prot) [ p.x, p.y, z ]
];
n = len(points);
r = [0:n-1];
faces = [
[ for (pi = r) pi ],
for (zi = [0:slices-1])
let(base = zi*n)
for (pi = r) [ base+pi, base+n+pi, base+n+(pi+1)%n ],
for (zi = [0:slices-1])
let(base = zi*n)
for (pi = r) [ base+pi, base+n+(pi+1)%n, base+(pi+1)%n ],
[ for (pi = [n-1:-1:0]) n*slices+pi ]
];
polyhedron(points=points3, faces=faces, convexity=convexity);
}

JB
Jordan Brown
Fri, May 27, 2022 1:44 AM
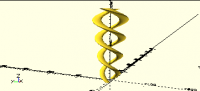
You can make related shapes with linear_extrude, but it's hard to get
right.
for (a = [0,180]) {
rotate(a)
linear_extrude(height=200, scale=2, twist=720, slices=100) {
translate([20,0]) circle(r=7);
}
}
One challenge is that you only get one "scale" argument, and so if you
want the radius of the snake body to increase, the radius of the helix
has to increase too.
Another is that it's remarkably difficult to get linear_extrude to
extrude a twisted cylinder. The problem is that linear extrude extrudes
from a horizontal cross-section, and the horizontal cross-section of a
twisted cylinder is not a circle - it's more of a crescent. (But that's
not right either.) I derived the correct shape once, but I don't
remember how. It might well have been using some horrible mechanism
like taking a cross-section of a sweep. And, of course, that's before
you try to get the diameter of the cylinder to change.
Net, I think your first bet is to use a sweep function. Beyond that,
especially if you want to add texture, I think you're in DIY polyhedron
territory. Adding texture would be... interesting... especially if you
don't want the texture to scale with the size of the triangle.
You *can* make related shapes with linear_extrude, but it's hard to get
right.
for (a = [0,180]) {
rotate(a)
linear_extrude(height=200, scale=2, twist=720, slices=100) {
translate([20,0]) circle(r=7);
}
}
One challenge is that you only get one "scale" argument, and so if you
want the radius of the snake body to increase, the radius of the helix
has to increase too.
Another is that it's remarkably difficult to get linear_extrude to
extrude a twisted cylinder. The problem is that linear extrude extrudes
from a horizontal cross-section, and the horizontal cross-section of a
twisted cylinder is not a circle - it's more of a crescent. (But that's
not right either.) I derived the correct shape once, but I don't
remember how. It might well have been using some horrible mechanism
like taking a cross-section of a sweep. And, of course, that's before
you try to get the diameter of the cylinder to change.
---
Net, I think your first bet is to use a sweep function. Beyond that,
especially if you want to add texture, I think you're in DIY polyhedron
territory. Adding texture would be... interesting... especially if you
don't want the texture to scale with the size of the triangle.

RW
Rogier Wolff
Fri, May 27, 2022 4:54 AM
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
Hmm. That leads to weird results.
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110 **
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
> Theoretically, linear_extrude could evaluate its child once for each
> step, and the child could do something different. (Spoiler: it doesn't
> work that way today.)
Hmm. That leads to weird results.
----------------------
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
----------------------
Roger.
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110 **
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a is going up. -- Chris Hadfield about flying up the space shuttle.

JB
Jordan Brown
Fri, May 27, 2022 5:38 AM
On 5/26/2022 9:54 PM, Rogier Wolff wrote:
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
Hmm. That leads to weird results.
I agree that it would lead to weird results (which might well be why it
isn't done that way), but your demonstration isn't that.
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
In the first case, you're creating a circle with a diameter of 2, and
across the extrusion scaling it up to a diameter of 10.
In the second case, you're creating a circle with a diameter of 10, and
scaling it down to a diameter of 2.
A default circle with a diameter of 2 is a pentagon. A default circle
with a diameter of 10 is a 16-gon. Scaling them up and down doesn't
change that.
It's actually a little tricky to show that linear_extrude isn't
re-evaluating its child for each layer. Well, OK, there's the easy way
of adding an "echo" and seeing how many times it's triggered, but that's
cheating. How can you do it so that the geometry would be different,
given that linear_extrude doesn't give you any handy $ variables? rands()!
The biggest reason I can see for not having linear_extrude evaluate the
child N times (other than performance) is that it's hard to figure out
what it would mean. You have N samples, each giving you a potentially
totally unrelated 2D figure. How would you connect them? Somebody's
probably done such a thing, probably some kind of hull-like operation,
but it's got to be enormously more complicated than "draw two triangles
between the four corresponding points".
On 5/26/2022 9:54 PM, Rogier Wolff wrote:
> On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
>> Theoretically, linear_extrude could evaluate its child once for each
>> step, and the child could do something different. (Spoiler: it doesn't
>> work that way today.)
> Hmm. That leads to weird results.
I agree that it would lead to weird results (which might well be why it
isn't done that way), but your demonstration isn't that.
> hh=15;
> bd = 10;
> s=5;
>
> translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
> translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
In the first case, you're creating a circle with a diameter of 2, and
across the extrusion scaling it up to a diameter of 10.
In the second case, you're creating a circle with a diameter of 10, and
scaling it down to a diameter of 2.
A default circle with a diameter of 2 is a pentagon. A default circle
with a diameter of 10 is a 16-gon. Scaling them up and down doesn't
change that.
---
It's actually a little tricky to show that linear_extrude isn't
re-evaluating its child for each layer. Well, OK, there's the easy way
of adding an "echo" and seeing how many times it's triggered, but that's
cheating. How can you do it so that the geometry would be different,
given that linear_extrude doesn't give you any handy $ variables? rands()!
---
The biggest reason I can see for not having linear_extrude evaluate the
child N times (other than performance) is that it's hard to figure out
what it would mean. You have N samples, each giving you a potentially
totally unrelated 2D figure. How would you connect them? Somebody's
probably done such a thing, probably some kind of hull-like operation,
but it's got to be enormously more complicated than "draw two triangles
between the four corresponding points".

AM
Adrian Mariano
Fri, May 27, 2022 12:06 PM
Ok. Here's a way to do it in BOSL2. I would normally do this with
sweep() and did that first, but then I noticed he says he wants the
polygons to change to create scales. That's going to be a pain with
sweep, so it's better to use skin(), which will connect a sequence of
arbitrary polygons. Note that skin() does not require that the
polygons have the same length. It will link up polygons with
different length and provides several algorithms for doing this
optimally (for different notions of optimal), though the "distance"
method has cubic run time so it's best suited to small polygons.
https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
polygons = [for (y=lerpn(0,l,steps))
apply(zrot(turns*360 *
y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 1:39 AM Jordan Brown
openscad@jordan.maileater.net wrote:
On 5/26/2022 9:54 PM, Rogier Wolff wrote:
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
Hmm. That leads to weird results.
I agree that it would lead to weird results (which might well be why it isn't done that way), but your demonstration isn't that.
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
In the first case, you're creating a circle with a diameter of 2, and across the extrusion scaling it up to a diameter of 10.
In the second case, you're creating a circle with a diameter of 10, and scaling it down to a diameter of 2.
A default circle with a diameter of 2 is a pentagon. A default circle with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change that.
It's actually a little tricky to show that linear_extrude isn't re-evaluating its child for each layer. Well, OK, there's the easy way of adding an "echo" and seeing how many times it's triggered, but that's cheating. How can you do it so that the geometry would be different, given that linear_extrude doesn't give you any handy $ variables? rands()!
The biggest reason I can see for not having linear_extrude evaluate the child N times (other than performance) is that it's hard to figure out what it would mean. You have N samples, each giving you a potentially totally unrelated 2D figure. How would you connect them? Somebody's probably done such a thing, probably some kind of hull-like operation, but it's got to be enormously more complicated than "draw two triangles between the four corresponding points".
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Ok. Here's a way to do it in BOSL2. I would normally do this with
sweep() and did that first, but then I noticed he says he wants the
polygons to change to create scales. That's going to be a pain with
sweep, so it's better to use skin(), which will connect a sequence of
arbitrary polygons. Note that skin() does not require that the
polygons have the same length. It will link up polygons with
different length and provides several algorithms for doing this
optimally (for different notions of optimal), though the "distance"
method has cubic run time so it's best suited to small polygons.
https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
polygons = [for (y=lerpn(0,l,steps))
apply(zrot(turns*360 *
y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 1:39 AM Jordan Brown
<openscad@jordan.maileater.net> wrote:
>
> On 5/26/2022 9:54 PM, Rogier Wolff wrote:
>
> On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
>
> Theoretically, linear_extrude could evaluate its child once for each
> step, and the child could do something different. (Spoiler: it doesn't
> work that way today.)
>
> Hmm. That leads to weird results.
>
>
> I agree that it would lead to weird results (which might well be why it isn't done that way), but your demonstration isn't that.
>
> hh=15;
> bd = 10;
> s=5;
>
> translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
> translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
>
>
> In the first case, you're creating a circle with a diameter of 2, and across the extrusion scaling it up to a diameter of 10.
> In the second case, you're creating a circle with a diameter of 10, and scaling it down to a diameter of 2.
>
> A default circle with a diameter of 2 is a pentagon. A default circle with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change that.
>
> ---
>
> It's actually a little tricky to show that linear_extrude isn't re-evaluating its child for each layer. Well, OK, there's the easy way of adding an "echo" and seeing how many times it's triggered, but that's cheating. How can you do it so that the geometry would be different, given that linear_extrude doesn't give you any handy $ variables? rands()!
>
> ---
>
> The biggest reason I can see for not having linear_extrude evaluate the child N times (other than performance) is that it's hard to figure out what it would mean. You have N samples, each giving you a potentially totally unrelated 2D figure. How would you connect them? Somebody's probably done such a thing, probably some kind of hull-like operation, but it's got to be enormously more complicated than "draw two triangles between the four corresponding points".
>
>
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

AM
Adrian Mariano
Fri, May 27, 2022 1:01 PM
It occurred to me that if the original interest is in making a snake
spiral then really the linear extrude approach doesn't work at all,
because it produces a progressively flatter shape. You need to use an
elliptical cross section, which changes as the curvature of the helix
changes---based on the sine of the angle, I suppose. The only easy
way to get this right is with a path sweep operation that keeps the
snake body perpendicular to the path, e.g.:
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
path_sweep(circle(r=1,$fn=resolution), path =
[for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])]);
}
schlange();
All is not lost for adding scales, though. You can still convert this
approach to use skin() by using the transforms option to path_sweep().
I've written this below so the polygon list is constructed based on a
numerical index could be used for the scale pattern.
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
T = path_sweep(path = [for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])],
transforms=true);
polygons = [for(i=idx(T)) apply(T[i],path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 8:06 AM Adrian Mariano avm4@cornell.edu wrote:
Ok. Here's a way to do it in BOSL2. I would normally do this with
sweep() and did that first, but then I noticed he says he wants the
polygons to change to create scales. That's going to be a pain with
sweep, so it's better to use skin(), which will connect a sequence of
arbitrary polygons. Note that skin() does not require that the
polygons have the same length. It will link up polygons with
different length and provides several algorithms for doing this
optimally (for different notions of optimal), though the "distance"
method has cubic run time so it's best suited to small polygons.
https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
polygons = [for (y=lerpn(0,l,steps))
apply(zrot(turns*360 *
y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 1:39 AM Jordan Brown
openscad@jordan.maileater.net wrote:
On 5/26/2022 9:54 PM, Rogier Wolff wrote:
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
Hmm. That leads to weird results.
I agree that it would lead to weird results (which might well be why it isn't done that way), but your demonstration isn't that.
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
In the first case, you're creating a circle with a diameter of 2, and across the extrusion scaling it up to a diameter of 10.
In the second case, you're creating a circle with a diameter of 10, and scaling it down to a diameter of 2.
A default circle with a diameter of 2 is a pentagon. A default circle with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change that.
It's actually a little tricky to show that linear_extrude isn't re-evaluating its child for each layer. Well, OK, there's the easy way of adding an "echo" and seeing how many times it's triggered, but that's cheating. How can you do it so that the geometry would be different, given that linear_extrude doesn't give you any handy $ variables? rands()!
The biggest reason I can see for not having linear_extrude evaluate the child N times (other than performance) is that it's hard to figure out what it would mean. You have N samples, each giving you a potentially totally unrelated 2D figure. How would you connect them? Somebody's probably done such a thing, probably some kind of hull-like operation, but it's got to be enormously more complicated than "draw two triangles between the four corresponding points".
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
It occurred to me that if the original interest is in making a snake
spiral then really the linear extrude approach doesn't work at all,
because it produces a progressively flatter shape. You need to use an
elliptical cross section, which changes as the curvature of the helix
changes---based on the sine of the angle, I suppose. The only easy
way to get this right is with a path sweep operation that keeps the
snake body perpendicular to the path, e.g.:
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
path_sweep(circle(r=1,$fn=resolution), path =
[for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])]);
}
schlange();
All is not lost for adding scales, though. You can still convert this
approach to use skin() by using the transforms option to path_sweep().
I've written this below so the polygon list is constructed based on a
numerical index could be used for the scale pattern.
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
T = path_sweep(path = [for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])],
transforms=true);
polygons = [for(i=idx(T)) apply(T[i],path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 8:06 AM Adrian Mariano <avm4@cornell.edu> wrote:
>
> Ok. Here's a way to do it in BOSL2. I would normally do this with
> sweep() and did that first, but then I noticed he says he wants the
> polygons to change to create scales. That's going to be a pain with
> sweep, so it's better to use skin(), which will connect a sequence of
> arbitrary polygons. Note that skin() does not require that the
> polygons have the same length. It will link up polygons with
> different length and provides several algorithms for doing this
> optimally (for different notions of optimal), though the "distance"
> method has cubic run time so it's best suited to small polygons.
>
> https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
>
> include <BOSL2/std.scad>
>
> function schlrad(d,l,y)=d/l*(y+l/2/d);
>
> module schlange(l=20,d=2,resolution = 12, turns=3)
> {
> steps = 75;
> polygons = [for (y=lerpn(0,l,steps))
> apply(zrot(turns*360 *
> y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
> skin(polygons,slices=0);
> }
>
> schlange();
>
> On Fri, May 27, 2022 at 1:39 AM Jordan Brown
> <openscad@jordan.maileater.net> wrote:
> >
> > On 5/26/2022 9:54 PM, Rogier Wolff wrote:
> >
> > On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
> >
> > Theoretically, linear_extrude could evaluate its child once for each
> > step, and the child could do something different. (Spoiler: it doesn't
> > work that way today.)
> >
> > Hmm. That leads to weird results.
> >
> >
> > I agree that it would lead to weird results (which might well be why it isn't done that way), but your demonstration isn't that.
> >
> > hh=15;
> > bd = 10;
> > s=5;
> >
> > translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
> > translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
> >
> >
> > In the first case, you're creating a circle with a diameter of 2, and across the extrusion scaling it up to a diameter of 10.
> > In the second case, you're creating a circle with a diameter of 10, and scaling it down to a diameter of 2.
> >
> > A default circle with a diameter of 2 is a pentagon. A default circle with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change that.
> >
> > ---
> >
> > It's actually a little tricky to show that linear_extrude isn't re-evaluating its child for each layer. Well, OK, there's the easy way of adding an "echo" and seeing how many times it's triggered, but that's cheating. How can you do it so that the geometry would be different, given that linear_extrude doesn't give you any handy $ variables? rands()!
> >
> > ---
> >
> > The biggest reason I can see for not having linear_extrude evaluate the child N times (other than performance) is that it's hard to figure out what it would mean. You have N samples, each giving you a potentially totally unrelated 2D figure. How would you connect them? Somebody's probably done such a thing, probably some kind of hull-like operation, but it's got to be enormously more complicated than "draw two triangles between the four corresponding points".
> >
> >
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org

RW
Raymond West
Fri, May 27, 2022 2:53 PM
module snake(){
for(j=[80:200]){
rotate([0,0,j10])
translate([j0.1,j0.1,j3])
sphere(d=(j*0.05));
}
}
snake();
rotate([0,0,180])snake();
cylinder(h=650,d=12);
Fn6 takes a while ;)
On 27/05/2022 14:01, Adrian Mariano wrote:
It occurred to me that if the original interest is in making a snake
spiral then really the linear extrude approach doesn't work at all,
because it produces a progressively flatter shape. You need to use an
elliptical cross section, which changes as the curvature of the helix
changes---based on the sine of the angle, I suppose. The only easy
way to get this right is with a path sweep operation that keeps the
snake body perpendicular to the path, e.g.:
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
path_sweep(circle(r=1,$fn=resolution), path =
[for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])]);
}
schlange();
All is not lost for adding scales, though. You can still convert this
approach to use skin() by using the transforms option to path_sweep().
I've written this below so the polygon list is constructed based on a
numerical index could be used for the scale pattern.
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
T = path_sweep(path = [for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])],
transforms=true);
polygons = [for(i=idx(T)) apply(T[i],path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 8:06 AM Adrian Mariano avm4@cornell.edu wrote:
Ok. Here's a way to do it in BOSL2. I would normally do this with
sweep() and did that first, but then I noticed he says he wants the
polygons to change to create scales. That's going to be a pain with
sweep, so it's better to use skin(), which will connect a sequence of
arbitrary polygons. Note that skin() does not require that the
polygons have the same length. It will link up polygons with
different length and provides several algorithms for doing this
optimally (for different notions of optimal), though the "distance"
method has cubic run time so it's best suited to small polygons.
https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
polygons = [for (y=lerpn(0,l,steps))
apply(zrot(turns*360 *
y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 1:39 AM Jordan Brown
openscad@jordan.maileater.net wrote:
On 5/26/2022 9:54 PM, Rogier Wolff wrote:
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it doesn't
work that way today.)
Hmm. That leads to weird results.
I agree that it would lead to weird results (which might well be why it isn't done that way), but your demonstration isn't that.
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
In the first case, you're creating a circle with a diameter of 2, and across the extrusion scaling it up to a diameter of 10.
In the second case, you're creating a circle with a diameter of 10, and scaling it down to a diameter of 2.
A default circle with a diameter of 2 is a pentagon. A default circle with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change that.
It's actually a little tricky to show that linear_extrude isn't re-evaluating its child for each layer. Well, OK, there's the easy way of adding an "echo" and seeing how many times it's triggered, but that's cheating. How can you do it so that the geometry would be different, given that linear_extrude doesn't give you any handy $ variables? rands()!
The biggest reason I can see for not having linear_extrude evaluate the child N times (other than performance) is that it's hard to figure out what it would mean. You have N samples, each giving you a potentially totally unrelated 2D figure. How would you connect them? Somebody's probably done such a thing, probably some kind of hull-like operation, but it's got to be enormously more complicated than "draw two triangles between the four corresponding points".
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
module snake(){
for(j=[80:200]){
rotate([0,0,j*10])
translate([j*0.1,j*0.1,j*3])
sphere(d=(j*0.05));
}
}
snake();
rotate([0,0,180])snake();
cylinder(h=650,d=12);
Fn6 takes a while ;)
On 27/05/2022 14:01, Adrian Mariano wrote:
> It occurred to me that if the original interest is in making a snake
> spiral then really the linear extrude approach doesn't work at all,
> because it produces a progressively flatter shape. You need to use an
> elliptical cross section, which changes as the curvature of the helix
> changes---based on the sine of the angle, I suppose. The only easy
> way to get this right is with a path sweep operation that keeps the
> snake body perpendicular to the path, e.g.:
>
> include <BOSL2/std.scad>
>
> function schlrad(d,l,y)=d/l*(y+l/2/d);
>
> module schlange(l=20,d=2,resolution = 12, turns=3)
> {
> steps = 75;
> path_sweep(circle(r=1,$fn=resolution), path =
> [for(y=lerpn(0,l,steps))
> zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])]);
> }
>
> schlange();
>
> All is not lost for adding scales, though. You can still convert this
> approach to use skin() by using the transforms option to path_sweep().
> I've written this below so the polygon list is constructed based on a
> numerical index could be used for the scale pattern.
>
> include <BOSL2/std.scad>
>
> function schlrad(d,l,y)=d/l*(y+l/2/d);
>
> module schlange(l=20,d=2,resolution = 12, turns=3)
> {
> steps = 75;
> T = path_sweep(path = [for(y=lerpn(0,l,steps))
> zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])],
> transforms=true);
> polygons = [for(i=idx(T)) apply(T[i],path3d(circle(r=1,$fn=resolution)))];
> skin(polygons,slices=0);
> }
>
> schlange();
>
> On Fri, May 27, 2022 at 8:06 AM Adrian Mariano <avm4@cornell.edu> wrote:
>> Ok. Here's a way to do it in BOSL2. I would normally do this with
>> sweep() and did that first, but then I noticed he says he wants the
>> polygons to change to create scales. That's going to be a pain with
>> sweep, so it's better to use skin(), which will connect a sequence of
>> arbitrary polygons. Note that skin() does not require that the
>> polygons have the same length. It will link up polygons with
>> different length and provides several algorithms for doing this
>> optimally (for different notions of optimal), though the "distance"
>> method has cubic run time so it's best suited to small polygons.
>>
>> https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
>>
>> include <BOSL2/std.scad>
>>
>> function schlrad(d,l,y)=d/l*(y+l/2/d);
>>
>> module schlange(l=20,d=2,resolution = 12, turns=3)
>> {
>> steps = 75;
>> polygons = [for (y=lerpn(0,l,steps))
>> apply(zrot(turns*360 *
>> y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
>> skin(polygons,slices=0);
>> }
>>
>> schlange();
>>
>> On Fri, May 27, 2022 at 1:39 AM Jordan Brown
>> <openscad@jordan.maileater.net> wrote:
>>> On 5/26/2022 9:54 PM, Rogier Wolff wrote:
>>>
>>> On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
>>>
>>> Theoretically, linear_extrude could evaluate its child once for each
>>> step, and the child could do something different. (Spoiler: it doesn't
>>> work that way today.)
>>>
>>> Hmm. That leads to weird results.
>>>
>>>
>>> I agree that it would lead to weird results (which might well be why it isn't done that way), but your demonstration isn't that.
>>>
>>> hh=15;
>>> bd = 10;
>>> s=5;
>>>
>>> translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle (d=bd/s);
>>> translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle (d=bd);
>>>
>>>
>>> In the first case, you're creating a circle with a diameter of 2, and across the extrusion scaling it up to a diameter of 10.
>>> In the second case, you're creating a circle with a diameter of 10, and scaling it down to a diameter of 2.
>>>
>>> A default circle with a diameter of 2 is a pentagon. A default circle with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change that.
>>>
>>> ---
>>>
>>> It's actually a little tricky to show that linear_extrude isn't re-evaluating its child for each layer. Well, OK, there's the easy way of adding an "echo" and seeing how many times it's triggered, but that's cheating. How can you do it so that the geometry would be different, given that linear_extrude doesn't give you any handy $ variables? rands()!
>>>
>>> ---
>>>
>>> The biggest reason I can see for not having linear_extrude evaluate the child N times (other than performance) is that it's hard to figure out what it would mean. You have N samples, each giving you a potentially totally unrelated 2D figure. How would you connect them? Somebody's probably done such a thing, probably some kind of hull-like operation, but it's got to be enormously more complicated than "draw two triangles between the four corresponding points".
>>>
>>>
>>> _______________________________________________
>>> OpenSCAD mailing list
>>> To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org

BB
Bruno Boettcher
Fri, May 27, 2022 3:53 PM
Thanks Adriano,
that ones nice, i can base myself on that one!
Am Fr., 27. Mai 2022 um 15:01 Uhr schrieb Adrian Mariano avm4@cornell.edu:
It occurred to me that if the original interest is in making a snake
spiral then really the linear extrude approach doesn't work at all,
because it produces a progressively flatter shape. You need to use an
elliptical cross section, which changes as the curvature of the helix
changes---based on the sine of the angle, I suppose. The only easy
way to get this right is with a path sweep operation that keeps the
snake body perpendicular to the path, e.g.:
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
path_sweep(circle(r=1,$fn=resolution), path =
[for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])]);
}
schlange();
All is not lost for adding scales, though. You can still convert this
approach to use skin() by using the transforms option to path_sweep().
I've written this below so the polygon list is constructed based on a
numerical index could be used for the scale pattern.
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
T = path_sweep(path = [for(y=lerpn(0,l,steps))
zrot(turns*360 * y/l,
[schlrad(d=d,l=l,y=y),0,y])],
transforms=true);
polygons = [for(i=idx(T))
apply(T[i],path3d(circle(r=1,$fn=resolution)))];
skin(polygons,slices=0);
}
schlange();
On Fri, May 27, 2022 at 8:06 AM Adrian Mariano avm4@cornell.edu wrote:
Ok. Here's a way to do it in BOSL2. I would normally do this with
sweep() and did that first, but then I noticed he says he wants the
polygons to change to create scales. That's going to be a pain with
sweep, so it's better to use skin(), which will connect a sequence of
arbitrary polygons. Note that skin() does not require that the
polygons have the same length. It will link up polygons with
different length and provides several algorithms for doing this
optimally (for different notions of optimal), though the "distance"
method has cubic run time so it's best suited to small polygons.
https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
include <BOSL2/std.scad>
function schlrad(d,l,y)=d/l*(y+l/2/d);
module schlange(l=20,d=2,resolution = 12, turns=3)
{
steps = 75;
polygons = [for (y=lerpn(0,l,steps))
apply(zrot(turns*360 *
y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
On 5/26/2022 9:54 PM, Rogier Wolff wrote:
On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
Theoretically, linear_extrude could evaluate its child once for each
step, and the child could do something different. (Spoiler: it
work that way today.)
Hmm. That leads to weird results.
I agree that it would lead to weird results (which might well be why
it isn't done that way), but your demonstration isn't that.
hh=15;
bd = 10;
s=5;
translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle
translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle
In the first case, you're creating a circle with a diameter of 2, and
across the extrusion scaling it up to a diameter of 10.
In the second case, you're creating a circle with a diameter of 10,
and scaling it down to a diameter of 2.
A default circle with a diameter of 2 is a pentagon. A default circle
with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change
that.
It's actually a little tricky to show that linear_extrude isn't
re-evaluating its child for each layer. Well, OK, there's the easy way of
adding an "echo" and seeing how many times it's triggered, but that's
cheating. How can you do it so that the geometry would be different, given
that linear_extrude doesn't give you any handy $ variables? rands()!
The biggest reason I can see for not having linear_extrude evaluate
the child N times (other than performance) is that it's hard to figure out
what it would mean. You have N samples, each giving you a potentially
totally unrelated 2D figure. How would you connect them? Somebody's
probably done such a thing, probably some kind of hull-like operation, but
it's got to be enormously more complicated than "draw two triangles between
the four corresponding points".
Thanks Adriano,
that ones nice, i can base myself on that one!
Am Fr., 27. Mai 2022 um 15:01 Uhr schrieb Adrian Mariano <avm4@cornell.edu>:
> It occurred to me that if the original interest is in making a snake
> spiral then really the linear extrude approach doesn't work at all,
> because it produces a progressively flatter shape. You need to use an
> elliptical cross section, which changes as the curvature of the helix
> changes---based on the sine of the angle, I suppose. The only easy
> way to get this right is with a path sweep operation that keeps the
> snake body perpendicular to the path, e.g.:
>
> include <BOSL2/std.scad>
>
> function schlrad(d,l,y)=d/l*(y+l/2/d);
>
> module schlange(l=20,d=2,resolution = 12, turns=3)
> {
> steps = 75;
> path_sweep(circle(r=1,$fn=resolution), path =
> [for(y=lerpn(0,l,steps))
> zrot(turns*360 * y/l, [schlrad(d=d,l=l,y=y),0,y])]);
> }
>
> schlange();
>
> All is not lost for adding scales, though. You can still convert this
> approach to use skin() by using the transforms option to path_sweep().
> I've written this below so the polygon list is constructed based on a
> numerical index could be used for the scale pattern.
>
> include <BOSL2/std.scad>
>
> function schlrad(d,l,y)=d/l*(y+l/2/d);
>
> module schlange(l=20,d=2,resolution = 12, turns=3)
> {
> steps = 75;
> T = path_sweep(path = [for(y=lerpn(0,l,steps))
> zrot(turns*360 * y/l,
> [schlrad(d=d,l=l,y=y),0,y])],
> transforms=true);
> polygons = [for(i=idx(T))
> apply(T[i],path3d(circle(r=1,$fn=resolution)))];
> skin(polygons,slices=0);
> }
>
> schlange();
>
> On Fri, May 27, 2022 at 8:06 AM Adrian Mariano <avm4@cornell.edu> wrote:
> >
> > Ok. Here's a way to do it in BOSL2. I would normally do this with
> > sweep() and did that first, but then I noticed he says he wants the
> > polygons to change to create scales. That's going to be a pain with
> > sweep, so it's better to use skin(), which will connect a sequence of
> > arbitrary polygons. Note that skin() does not require that the
> > polygons have the same length. It will link up polygons with
> > different length and provides several algorithms for doing this
> > optimally (for different notions of optimal), though the "distance"
> > method has cubic run time so it's best suited to small polygons.
> >
> > https://github.com/revarbat/BOSL2/wiki/skin.scad#functionmodule-skin
> >
> > include <BOSL2/std.scad>
> >
> > function schlrad(d,l,y)=d/l*(y+l/2/d);
> >
> > module schlange(l=20,d=2,resolution = 12, turns=3)
> > {
> > steps = 75;
> > polygons = [for (y=lerpn(0,l,steps))
> > apply(zrot(turns*360 *
> >
> y/l)*move([schlrad(d=d,l=l,y=y),0,y]),path3d(circle(r=1,$fn=resolution)))];
> > skin(polygons,slices=0);
> > }
> >
> > schlange();
> >
> > On Fri, May 27, 2022 at 1:39 AM Jordan Brown
> > <openscad@jordan.maileater.net> wrote:
> > >
> > > On 5/26/2022 9:54 PM, Rogier Wolff wrote:
> > >
> > > On Thu, May 26, 2022 at 06:21:36PM -0700, Jordan Brown wrote:
> > >
> > > Theoretically, linear_extrude could evaluate its child once for each
> > > step, and the child could do something different. (Spoiler: it
> doesn't
> > > work that way today.)
> > >
> > > Hmm. That leads to weird results.
> > >
> > >
> > > I agree that it would lead to weird results (which might well be why
> it isn't done that way), but your demonstration isn't that.
> > >
> > > hh=15;
> > > bd = 10;
> > > s=5;
> > >
> > > translate ([0,0,-hh]) linear_extrude (height=hh, scale= s) circle
> (d=bd/s);
> > > translate ([0,0, 0]) linear_extrude (height=hh, scale=1/s) circle
> (d=bd);
> > >
> > >
> > > In the first case, you're creating a circle with a diameter of 2, and
> across the extrusion scaling it up to a diameter of 10.
> > > In the second case, you're creating a circle with a diameter of 10,
> and scaling it down to a diameter of 2.
> > >
> > > A default circle with a diameter of 2 is a pentagon. A default circle
> with a diameter of 10 is a 16-gon. Scaling them up and down doesn't change
> that.
> > >
> > > ---
> > >
> > > It's actually a little tricky to show that linear_extrude isn't
> re-evaluating its child for each layer. Well, OK, there's the easy way of
> adding an "echo" and seeing how many times it's triggered, but that's
> cheating. How can you do it so that the geometry would be different, given
> that linear_extrude doesn't give you any handy $ variables? rands()!
> > >
> > > ---
> > >
> > > The biggest reason I can see for not having linear_extrude evaluate
> the child N times (other than performance) is that it's hard to figure out
> what it would mean. You have N samples, each giving you a potentially
> totally unrelated 2D figure. How would you connect them? Somebody's
> probably done such a thing, probably some kind of hull-like operation, but
> it's got to be enormously more complicated than "draw two triangles between
> the four corresponding points".
> > >
> > >
> > > _______________________________________________
> > > OpenSCAD mailing list
> > > To unsubscribe send an email to discuss-leave@lists.openscad.org
> _______________________________________________
> OpenSCAD mailing list
> To unsubscribe send an email to discuss-leave@lists.openscad.org
>
--
ciao
Bruno
===========================================
http://nohkumado.eu/, <http://bboett.free.fr>http://aikido.nohkumado.eu/,
<http://bboett.free.fr>
http://aikido.zorn.free.fr


