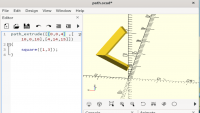
Path sweep
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done
using native modules and functions alone (i.e. without "cheating" by
using polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
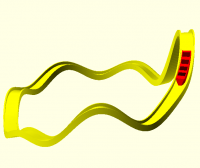
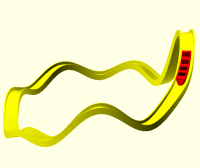
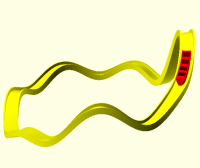
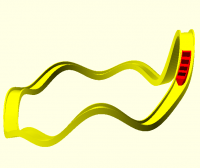
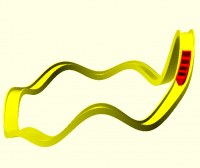
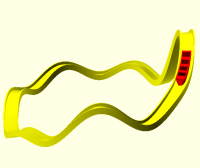
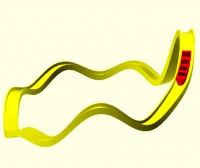
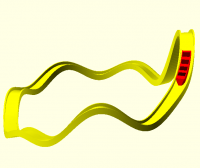
For example, this Möbius strip is made by sweeping an elongated ellipse
along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360), 0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and sweeping
a triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the
same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn =
500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm
chasing something impossible.
But this problem didn't hamper my accurate scale modeling of the St.
Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both
the scaling and rotation unambiguously.
Regards,
Curt
I feel the approach for common users should be such that when a separate
path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little complicated for
different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss <
discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done using
native modules and functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
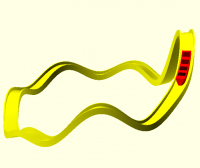
For example, this Möbius strip is made by sweeping an elongated ellipse
along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360), 0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and sweeping a
triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the same
parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn = 500)
{
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm chasing
something impossible.
But this problem didn't hamper my accurate scale modeling of the St. Louis
Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
But, what if you wanted to scale and rotate the section along the path?
Then, instead of just a path, would you then need to specify multiple equal
length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that when a separate
path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little complicated for
different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss <
discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done using
native modules and functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an elongated ellipse
along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360), 0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and sweeping
a triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the
same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn =
500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm chasing
something impossible.
But this problem didn't hamper my accurate scale modeling of the St.
Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On 3/2/2024 6:09 PM, Leonard Martin Struttmann via Discuss wrote:
But, what if you wanted to scale and rotate the section along the
path? Then, instead of just a path, would you then need to specify
multiple equal length lists?
sweep(section,path,angles,scalings)
Just a thought.
I believe that fully general sweep functions accept a list of
transformation matrixes to modify the shape along the path.
Or they call a function to generate the shape.
Or they take a list of shapes along the path, which is much harder.
I know what you are saying here, but it will make things a little complex.
Once you have a generic path extrude or sweep function, the other
modifications can be implemented.
A simple path extrude function should be much easier to implement.
On Sun, 3 Mar, 2024, 7:39 am Leonard Martin Struttmann via Discuss, <
discuss@lists.openscad.org> wrote:
But, what if you wanted to scale and rotate the section along the path?
Then, instead of just a path, would you then need to specify multiple equal
length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that when a separate
path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little complicated for
different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss <
discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done using
native modules and functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an elongated ellipse
along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360), 0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and sweeping
a triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the
same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn =
500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3, 3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm chasing
something impossible.
But this problem didn't hamper my accurate scale modeling of the St.
Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Guys,
The path_extrude in my fork where previews are available at pythonscad.org
is an openscad-internal solution.
It even works correctly when only using very few slices because the 2D
shape is skewed in such a way that any perpendicular x-section of the
result
will always be the extruded polygon, even in corners of the extruded path.
And of course you can extrude any shape...
[image: image.png]
On Sun, Mar 3, 2024 at 4:31 AM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I know what you are saying here, but it will make things a little complex.
Once you have a generic path extrude or sweep function, the other
modifications can be implemented.
A simple path extrude function should be much easier to implement.
On Sun, 3 Mar, 2024, 7:39 am Leonard Martin Struttmann via Discuss, <
discuss@lists.openscad.org> wrote:
But, what if you wanted to scale and rotate the section along the path?
Then, instead of just a path, would you then need to specify multiple equal
length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that when a separate
path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little complicated for
different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss <
discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done using
native modules and functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an elongated ellipse
along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360),
0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and
sweeping a triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the
same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn =
500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3,
3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3,
3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm chasing
something impossible.
But this problem didn't hamper my accurate scale modeling of the St.
Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
But these have been implemented many, many times before, and are
available in libraries. Why are you reinventing the wheel? For fun?
On 3/2/2024 10:30 PM, Sanjeev Prabhakar via Discuss wrote:
I know what you are saying here, but it will make things a little
complex.
Once you have a generic path extrude or sweep function, the other
modifications can be implemented.
A simple path extrude function should be much easier to implement.
On Sun, 3 Mar, 2024, 7:39 am Leonard Martin Struttmann via Discuss,
discuss@lists.openscad.org wrote:
But, what if you wanted to scale and rotate the section along the
path? Then, instead of just a path, would you then need to
specify multiple equal length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss
<discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that when
a separate path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little
complicated for different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss
<discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear
extrude led me to explore path sweeping. I came up with
this very general module, done using native modules and
functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and
convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an
elongated ellipse along a circle with 180 degrees of twist
along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 *
cos(t * 360), 0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the
helix, and sweeping a triangle. It's OK but suffering a
Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps
all along the same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale =
function(t) 1, $fn = 500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2],
[5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4],
[-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5,
4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne -
ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6],
[3, 6], [3, 3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6],
[3, 6], [3, 3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to
[0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1],
[w, 6.1], [w, 3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1],
[w, 6.1], [w, 3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1],
[w, 6.1], [w, 3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1],
[w, 6.1], [w, 3.2]]);
}
}
}
Where I began to realize a fundamental problem was
implementing a Lissajous sweep. I got four unexpected
abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining
the twist and needs some tweaking, probably to break it
into cases to handle some direction sensitivities in the
atan2 formulas. Either that, or I'm chasing something
impossible.
But this problem didn't hamper my accurate scale modeling
of the St. Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of
specifying functions for path, scale and angle, the user
specifies a path and a "rail". The rail is essentially
another path vaguely parallel to the original, that the
edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to
discuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
--
This email has been checked for viruses by AVG antivirus software.
www.avg.com
Not everyone uses the libraries and many prefer only native openSCAD.
This is my personal view to incorporate some useful functions like
path_extrude etc to openSCAD without any support from any library.
On Sun, 3 Mar 2024 at 19:11, jon jon@jonbondy.com wrote:
But these have been implemented many, many times before, and are available
in libraries. Why are you reinventing the wheel? For fun?
On 3/2/2024 10:30 PM, Sanjeev Prabhakar via Discuss wrote:
I know what you are saying here, but it will make things a little complex.
Once you have a generic path extrude or sweep function, the other
modifications can be implemented.
A simple path extrude function should be much easier to implement.
On Sun, 3 Mar, 2024, 7:39 am Leonard Martin Struttmann via Discuss, <
discuss@lists.openscad.org> wrote:
But, what if you wanted to scale and rotate the section along the path?
Then, instead of just a path, would you then need to specify multiple equal
length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that when a separate
path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little complicated for
different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss <
discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done using
native modules and functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an elongated ellipse
along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360),
0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and
sweeping a triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the
same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn =
500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3,
3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3,
3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm chasing
something impossible.
But this problem didn't hamper my accurate scale modeling of the St.
Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient
Virus-free.www.avg.com
http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient
<#m_-4923069795440476616_DAB4FAD8-2DD7-40BB-A1B8-4E2AA1F9FDF2>
My personal view is not using existing libraries is a huge waste of my
time, unless you want to try to replicate something for fun. I am
deeply appreciative of the BOSL2 library, for example.
I guess we each have our own perspective.
On 3/3/2024 10:04 AM, Sanjeev Prabhakar wrote:
Not everyone uses the libraries and many prefer only native openSCAD.
This is my personal view to incorporate some useful functions like
path_extrude etc to openSCAD without any support from any library.
On Sun, 3 Mar 2024 at 19:11, jon jon@jonbondy.com wrote:
But these have been implemented many, many times before, and are
available in libraries. Why are you reinventing the wheel? For fun?
On 3/2/2024 10:30 PM, Sanjeev Prabhakar via Discuss wrote:
I know what you are saying here, but it will make things a little
complex.
Once you have a generic path extrude or sweep function, the other
modifications can be implemented.
A simple path extrude function should be much easier to implement.
On Sun, 3 Mar, 2024, 7:39 am Leonard Martin Struttmann via
Discuss, <discuss@lists.openscad.org> wrote:
But, what if you wanted to scale and rotate the section along
the path? Then, instead of just a path, would you then need
to specify multiple equal length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss
<discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that
when a separate path and section is defined, it should
draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little
complicated for different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss
<discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear
extrude led me to explore path sweeping. I came up
with this very general module, done using native
modules and functions alone (i.e. without "cheating"
by using polyhedron and raw data points).
// Generalized module to sweep a 2D object where the
path,
// scale and angle are parameterized functions of t
(0 .. 1).
// Since hull() is used, the 2D object must be simple
and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 +
n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers
overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an
elongated ellipse along a circle with 180 degrees of
twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100
* cos(t * 360), 0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h /
pitch),
r * sin(t * 360 * h /
pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the
helix, and sweeping a triangle. It's OK but suffering
a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9
sweeps all along the same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale =
function(t) 1, $fn = 500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5,
2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4,
4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4],
[5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) /
(ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3,
6], [3, 6], [3, 3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3,
6], [3, 6], [3, 3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative
to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) //
front seat
polygon(points = [[-w, 3.2], [-w,
6.1], [w, 6.1], [w, 3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w,
6.1], [w, 6.1], [w, 3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w,
6.1], [w, 6.1], [w, 3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) //
back seat
polygon(points = [[-w, 3.2], [-w,
6.1], [w, 6.1], [w, 3.2]]);
}
}
}
Where I began to realize a fundamental problem was
implementing a Lissajous sweep. I got four unexpected
abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly
determining the twist and needs some tweaking,
probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either
that, or I'm chasing something impossible.
But this problem didn't hamper my accurate scale
modeling of the St. Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side
triangle
The way Fusion 360 does it might be better. Instead
of specifying functions for path, scale and angle,
the user specifies a path and a "rail". The rail is
essentially another path vaguely parallel to the
original, that the edge of the object stays attached
to, dictating both the scaling and rotation
unambiguously.
Regards,
Curt
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to
discuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to
discuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
<http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient>
Virus-free.www.avg.com
<http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient>
<#m_-4923069795440476616_DAB4FAD8-2DD7-40BB-A1B8-4E2AA1F9FDF2>
--
This email has been checked for viruses by AVG antivirus software.
www.avg.com
John, I am not used to using libraries either.
Key problem is that you have to include them in your project and you have
to make sure that you install them to your computer.
Then the issue multiplies if you happen to work on several computers and
you need to make sure that all computers are in sync with your favorite
libraries and latest versions.
I started once with the idea to develop a function library with code which
I apparently often reuse, but the issue was that they become unattractive
very soon, because I did not manage to sync all of them in their latest
version among my computers.
Then I did not use them and ultimately forgot about them ...
If you depend on the tools internal functions, they are just there and not
worrying about it (PLUS: they have very descriptive names, are intuitive
and come with lots of tutorials and documentation which is really easy to
digest.
Can't claim that from BOSL2 ...
Ultimately i was finding myself not using libraries
On Sun, Mar 3, 2024 at 6:19 PM jon via Discuss discuss@lists.openscad.org
wrote:
My personal view is not using existing libraries is a huge waste of my
time, unless you want to try to replicate something for fun. I am deeply
appreciative of the BOSL2 library, for example.
I guess we each have our own perspective.
On 3/3/2024 10:04 AM, Sanjeev Prabhakar wrote:
Not everyone uses the libraries and many prefer only native openSCAD.
This is my personal view to incorporate some useful functions like
path_extrude etc to openSCAD without any support from any library.
On Sun, 3 Mar 2024 at 19:11, jon jon@jonbondy.com wrote:
But these have been implemented many, many times before, and are
available in libraries. Why are you reinventing the wheel? For fun?
On 3/2/2024 10:30 PM, Sanjeev Prabhakar via Discuss wrote:
I know what you are saying here, but it will make things a little
complex.
Once you have a generic path extrude or sweep function, the other
modifications can be implemented.
A simple path extrude function should be much easier to implement.
On Sun, 3 Mar, 2024, 7:39 am Leonard Martin Struttmann via Discuss, <
discuss@lists.openscad.org> wrote:
But, what if you wanted to scale and rotate the section along the path?
Then, instead of just a path, would you then need to specify multiple equal
length lists?
sweep(section,path,angles,scalings)
Just a thought.
On Sat, Mar 2, 2024 at 7:04 PM Sanjeev Prabhakar via Discuss <
discuss@lists.openscad.org> wrote:
I feel the approach for common users should be such that when a
separate path and section is defined, it should draw the shape.
for example:
path can be an ellipse
section can be a circle
module should be:
sweep(section, path)
defining the shape as you have defined may be a little complicated for
different users (at least for me).
On Sun, 3 Mar 2024 at 02:20, Curt McDowell via Discuss <
discuss@lists.openscad.org> wrote:
The discussion about generating a helix with linear extrude led me to
explore path sweeping. I came up with this very general module, done using
native modules and functions alone (i.e. without "cheating" by using
polyhedron and raw data points).
// Generalized module to sweep a 2D object where the path,
// scale and angle are parameterized functions of t (0 .. 1).
// Since hull() is used, the 2D object must be simple and convex.
module sweep(path,
scale = function(t) 1,
angle = function(t) 0,
t_start = 0.0,
t_end = 1.0,
$epsilon = 1.0e-4) {
dt = (t_end - t_start) / $fn;
module slice(t) {
p = path(t);
n = path(t + dt) - p;
translate(p)
rotate([0,
90 - atan2(n.z, sqrt(n.x ^ 2 + n.y ^ 2)),
atan2(n.y, n.x)])
scale(max(scale(t), $epsilon))
linear_extrude($epsilon)
rotate(angle(t))
children();
}
for (s = [0 : $fn - 1])
hull() {
slice(t_start + s * dt)
children();
// Extra bit of thickness helps layers overlap
slice(t_start + (s + 1 + $epsilon) * dt)
children();
}
}
For example, this Möbius strip is made by sweeping an elongated
ellipse along a circle with 180 degrees of twist along the way.
module demo_mobius()
sweep(path = function(t) [100 * sin(t * 360), 100 * cos(t * 360),
0],
angle = function(t) t * 180,
$fn = 100)
scale([40, 6]) // elliptical cross section
circle(1);
The helix:
helix_path = function(r, h, pitch)
function(t) [r * cos(t * 360 * h / pitch),
r * sin(t * 360 * h / pitch),
h * t];
module helix(r, h, pitch, wire_r)
sweep(helix_path(r, h, pitch))
circle(wire_r);
helix(r = 10, h = 60, pitch = 15, wire_r = 5, $fn = 200);
Odd shape made by adding scaling and rotation to the helix, and
sweeping a triangle. It's OK but suffering a Moire effect.
sweep(path = helix_path(r = 10, h = 60, pitch = 15),
scale = function(t) 1 - 4 * (t - 0.5) ^ 2,
angle = function(t) t * 4 * 360,
$fn = 1500)
circle(5, $fn = 3); // triangle
A more complicated thing: Roller coaster using 9 sweeps all along the
same parametric path.
module demo_roller_coaster() {
module coast(t_start = 0, t_end = 1, scale = function(t) 1, $fn =
500) {
px = function(t) 60 * cos(t * 360);
py = function(t) 60 * sin(t * 360);
pz = function(t) (5 * cos(t * 360 * 7) +
10 * cos(t ^ 2 * 360 * 3) -
20 * cos(t ^ 4 * 360));
sweep(function(t) [ px(t), py(t), pz(t) ],
angle = function(t) 90,
scale = scale,
t_start = t_start,
t_end = t_end)
children();
}
color("yellow") { // track
coast() // base
polygon(points = [[-5, 0], [-5, 2], [5, 2], [5, 0]]);
coast() // left rail
polygon(points = [[-5, 0], [-5, 4], [-4, 4], [-4, 0]]);
coast() // right rail
polygon(points = [[5, 0], [4, 0], [4, 4], [5, 4]]);
}
color("red") { // car
difference() {
e = 0.008;
union() { // chassis
ns = 0.747;
ne = 0.756;
coast(ns, ne, // snub nose
scale = function(t) (t - ns) / (ne - ns),
$fn = 8)
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3,
3]]);
coast(ne, 0.800, $fn = 20) // body
polygon(points = [[-3, 3], [-3, 6], [3, 6], [3,
3]]);
}
w = 2.5; // seat width
s = 0.002; // seat start/end relative to [0.00 : 0.01]
coast(0.76 + s, 0.76 + e, $fn = 20) // front seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.77 + s, 0.77 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.78 + s, 0.78 + e, $fn = 20)
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
coast(0.79 + s, 0.79 + e, $fn = 20) // back seat
polygon(points = [[-w, 3.2], [-w, 6.1], [w, 6.1], [w,
3.2]]);
}
}
}
Where I began to realize a fundamental problem was implementing a
Lissajous sweep. I got four unexpected abrupt quarter-twists.
sweep(function(t) [30 * cos(90 + 360 * t * 5),
30 * sin(360 * t * 4),
30 * cos(360 * t * 3)],
$fn = 1000)
square(9, center = true);
So it's apparent that my code isn't properly determining the twist and
needs some tweaking, probably to break it into cases to handle some
direction sensitivities in the atan2 formulas. Either that, or I'm chasing
something impossible.
But this problem didn't hamper my accurate scale modeling of the St.
Louis Gateway Arch (1 unit = 1 foot):
module st_louis_gateway_arch()
let (X_max = 299.2239,
Y_max = 625.0925,
A = 68.7672,
B = 0.0100333,
cosh = function(x) (exp(x) + exp(-x)) / 2,
t2x = function(t) (t - 0.5) * 2 * X_max,
y = function(x) Y_max - A * (cosh(B * x) - 1.0),
Q = function(x) 1262.6651 - 1.81977 * y(x),
d = function(q) sqrt(q * 4 / sqrt(3)))
sweep(path = function(t) [t2x(t), 0, y(t2x(t))],
scale = function(t) d(Q(t2x(t))),
angle = function(t) 120,
$fn = 100)
circle(sqrt(3) / 3, $fn = 3); // unit-side triangle
The way Fusion 360 does it might be better. Instead of specifying
functions for path, scale and angle, the user specifies a path and a
"rail". The rail is essentially another path vaguely parallel to the
original, that the edge of the object stays attached to, dictating both the
scaling and rotation unambiguously.
Regards,
Curt
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient
Virus-free.www.avg.com
http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient
<#m_-5767088494335446513_m_-4923069795440476616_DAB4FAD8-2DD7-40BB-A1B8-4E2AA1F9FDF2>
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org