Rounded Polygon
I'm hoping to eventually work up a general algorithm for subdividing an
arbitrary shape/area so that it can then be cut out using macros/modules
which I'll be defining in OpenSCAD (so as to have a 3D preview of a
project) and in some other programming languages as well (METAPOST seems
possible, Javascript/TPL (Tool Path Language) another, Python, or LiveCode
distant possibilities.
Basically I want to be able to have rounded ends on the dividers in:
https://community.carbide3d.com/t/fitted-box-design-generator-underway/13437/2
[image: cncboxfitted_3x3_round_divider.png]
instead of the sharp points.
William
On Fri, May 3, 2019 at 11:32 AM adrianv avm4@cornell.edu wrote:
Yes, what I meant by "teardrop" is an edge which combines 45 degrees of a
circular arc with a bevel at 45 deg so that the edge can be 3d printed
without support---with the bevel down there are no unsupported areas at
lower than a 45 deg angle.
William Adams-2 wrote
Okay. Discussion of a list of two-dimensional shapes,
mathematical/programmatic techniques for dividing shapes into regions,
and
the possible shapes which one can use in such deconstruction.
I really don't understand your question. When people talk of dividing 2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
--
Sent from: http://forum.openscad.org/
OpenSCAD mailing list
Discuss@lists.openscad.org
http://lists.openscad.org/mailman/listinfo/discuss_lists.openscad.org
I would make the shape by a cylinder and two linear extrudes stacked on top
of each other. To round the divider I would use offset(r) offset(-2 * r)
offset(r). That leaves the dimension the same but rounds both internal an
external corners.
On Fri, 3 May 2019 at 16:55, William Adams will.adams@frycomm.com wrote:
I'm hoping to eventually work up a general algorithm for subdividing an
arbitrary shape/area so that it can then be cut out using macros/modules
which I'll be defining in OpenSCAD (so as to have a 3D preview of a
project) and in some other programming languages as well (METAPOST seems
possible, Javascript/TPL (Tool Path Language) another, Python, or LiveCode
distant possibilities.
Basically I want to be able to have rounded ends on the dividers in:
https://community.carbide3d.com/t/fitted-box-design-generator-underway/13437/2
[image: cncboxfitted_3x3_round_divider.png]
instead of the sharp points.
William
On Fri, May 3, 2019 at 11:32 AM adrianv avm4@cornell.edu wrote:
Yes, what I meant by "teardrop" is an edge which combines 45 degrees of a
circular arc with a bevel at 45 deg so that the edge can be 3d printed
without support---with the bevel down there are no unsupported areas at
lower than a 45 deg angle.
William Adams-2 wrote
Okay. Discussion of a list of two-dimensional shapes,
mathematical/programmatic techniques for dividing shapes into regions,
and
the possible shapes which one can use in such deconstruction.
I really don't understand your question. When people talk of dividing 2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
--
Sent from: http://forum.openscad.org/
OpenSCAD mailing list
Discuss@lists.openscad.org
http://lists.openscad.org/mailman/listinfo/discuss_lists.openscad.org
Thanks! I've got a module which I'm calling which checks for endmill shape
and either puts a ball-nose on it or not (debating on adding support for V
shapes as well).
On Fri, May 3, 2019 at 12:08 PM nop head nop.head@gmail.com wrote:
I would make the shape by a cylinder and two linear extrudes stacked on
top of each other. To round the divider I would use offset(r) offset(-2 *
r) offset(r). That leaves the dimension the same but rounds both internal
an external corners.
On Fri, 3 May 2019 at 16:55, William Adams will.adams@frycomm.com wrote:
I'm hoping to eventually work up a general algorithm for subdividing an
arbitrary shape/area so that it can then be cut out using macros/modules
which I'll be defining in OpenSCAD (so as to have a 3D preview of a
project) and in some other programming languages as well (METAPOST seems
possible, Javascript/TPL (Tool Path Language) another, Python, or LiveCode
distant possibilities.
Basically I want to be able to have rounded ends on the dividers in:
https://community.carbide3d.com/t/fitted-box-design-generator-underway/13437/2
[image: cncboxfitted_3x3_round_divider.png]
instead of the sharp points.
William
On Fri, May 3, 2019 at 11:32 AM adrianv avm4@cornell.edu wrote:
Yes, what I meant by "teardrop" is an edge which combines 45 degrees of a
circular arc with a bevel at 45 deg so that the edge can be 3d printed
without support---with the bevel down there are no unsupported areas at
lower than a 45 deg angle.
William Adams-2 wrote
Okay. Discussion of a list of two-dimensional shapes,
mathematical/programmatic techniques for dividing shapes into regions,
and
the possible shapes which one can use in such deconstruction.
I really don't understand your question. When people talk of dividing 2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
--
Sent from: http://forum.openscad.org/
OpenSCAD mailing list
Discuss@lists.openscad.org
http://lists.openscad.org/mailman/listinfo/discuss_lists.openscad.org
adrianv wrote
I really don't understand your question. When people talk of dividing 2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
For example, given a rectangular outline of a box, I might like to split
that box into two compartments, and then I might want to further split one
of those compartments into three compartments (but sliced in the opposite
direction).
I actually did write a module for doing this (for rectangular boxes and
subdivisions). It needs dusting off, though.
Ray
--
Sent from: http://forum.openscad.org/
That's exactly what I've been working up --- I got rectangles done, now I'm
starting in on circles, next will be regular polygons, then we'll see if we
can do ovals and other shapes.
William
On Fri, May 3, 2019 at 12:20 PM RayBellis openscad@ray.bellis.me.uk wrote:
adrianv wrote
I really don't understand your question. When people talk of dividing 2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
For example, given a rectangular outline of a box, I might like to split
that box into two compartments, and then I might want to further split one
of those compartments into three compartments (but sliced in the opposite
direction).
I actually did write a module for doing this (for rectangular boxes and
subdivisions). It needs dusting off, though.
Ray
--
Sent from: http://forum.openscad.org/
OpenSCAD mailing list
Discuss@lists.openscad.org
http://lists.openscad.org/mailman/listinfo/discuss_lists.openscad.org
I spent a LOT of time writing code to do this, and triangulation of
polygons. Dues to implementation issues I ended up implementing a
convexifyPolygon function which turns an arbitrary non-self-intersecting
polygon into a list of convex polygons, and a triangulariseConvexPolygon
which triangulates the convex polygons. To implement those I needed various
splitting and clipping functions
On Fri, 3 May 2019, 12:50 William Adams, will.adams@frycomm.com wrote:
That's exactly what I've been working up --- I got rectangles done, now
I'm starting in on circles, next will be regular polygons, then we'll see
if we can do ovals and other shapes.
William
On Fri, May 3, 2019 at 12:20 PM RayBellis openscad@ray.bellis.me.uk
wrote:
adrianv wrote
I really don't understand your question. When people talk of dividing
2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
For example, given a rectangular outline of a box, I might like to split
that box into two compartments, and then I might want to further split one
of those compartments into three compartments (but sliced in the opposite
direction).
I actually did write a module for doing this (for rectangular boxes and
subdivisions). It needs dusting off, though.
Ray
--
Sent from: http://forum.openscad.org/
OpenSCAD mailing list
Discuss@lists.openscad.org
http://lists.openscad.org/mailman/listinfo/discuss_lists.openscad.org
You just want to round the junctions? I think you can do that for an
arbitrary 2d shape using offset(), with something like this (which was
previously mentioned many posts ago on this thread):
module round2d(or, ir)
{
offset(or) offset(-ir-or) offset(delta=ir) children();
}
As long as your walls aren't too thin relative to the curvature you want
(which looks small in your examples) I think that the above will actually do
the job of rounding any box you want to make.
round2d(or=.4, ir=1){
difference(){
square([20,20],center=true);
square([18,18],center=true);
}
translate([10,0,0])
difference(){
circle(d=20);
circle(d=18);
}
}
If you set or>-0.5 then you get in trouble because the walls vanish. But if
you round the outside shape first (before cutting out the middle) you can
resolve this problem.
http://forum.openscad.org/file/t2477/roundedthing.png
I'm not sure what you mean about the "algorithm for subdividing" part of
your project, though.
--
Sent from: http://forum.openscad.org/
Can you be more specific about what you are trying to do? You want to divide
a circle up into compartments with circular arcs? I mean, it seems like the
basic task of dividing a region into smaller regions with paths is mainly
difficult due to the interface part of the problem: how do you specify what
you want to create?
William Adams-2 wrote
That's exactly what I've been working up --- I got rectangles done, now
I'm
starting in on circles, next will be regular polygons, then we'll see if
we
can do ovals and other shapes.
William
On Fri, May 3, 2019 at 12:20 PM RayBellis <
openscad@.me
> wrote:
adrianv wrote
I really don't understand your question. When people talk of dividing
2d
shapes into regions they usually mean triangulating the shape. But it
sounds like you mean something else. Maybe you should give a specific
example?
For example, given a rectangular outline of a box, I might like to split
that box into two compartments, and then I might want to further split
one
of those compartments into three compartments (but sliced in the opposite
direction).
I actually did write a module for doing this (for rectangular boxes and
subdivisions). It needs dusting off, though.
Ray
--
Sent from: http://forum.openscad.org/
OpenSCAD mailing list
Discuss@.openscad
Discuss@.openscad
--
Sent from: http://forum.openscad.org/
Here's another example of a rounded box, this time with a more complex shape.
Note how the rounded edges of the tips vanish in the roundover at the
bottom. (One of the challenges here is that the number of vertices is not
the same in each layer.)
http://forum.openscad.org/file/t2477/fstarbox1.png
http://forum.openscad.org/file/t2477/fstarbox2.png
--
Sent from: http://forum.openscad.org/
I would like to come back to our discussion of more than 1 month ago.
Em sáb, 6 de abr de 2019 às 17:01, Ronaldo Persiano rcmpersiano@gmail.com
escreveu:
Based on that considerations we could try to build a patch that meets the
C1 condition (and perhaps the C2 condition) at the joints. However, what we
really need is G1 and G2 continuity, that is a geometric differentiabilty
and not a parametric one. Hard stuff!
It was clear, I suppose, that there is no C1 triangular Bezier patch
(tripatch) that meets the conditions we were looking for to round the
corner of a cube. And we were looking for a C2 patch joint! Meanwhile, I
have studied the conditions for a G2 tripatch joint, that is, conditions
that assures a geometric continuity of first and second derivatives
instead of parametric continuity. In a G1 joint between two patches they
must have the same tangent plane at each joint point. A similar weaker
condition is demanded for G2 patch joints. Geometric conditions are in
general weaker than the parametric ones.
I will not present here the development and theoretical support of the G2
tripatch I have found. This development is a bit technical so I will just
show one solution for a tripatch with a G2 joint to round corners where
exactly 3 edges meet. It is intended to be considered for modeling
evaluation.
Fixing the 2 possible form factors, the control points of the standard 5th
degree tripatch is:
Q = [ [[0,1,1]],
[[0,1,0.68],[0,0.68,1]],
[[0,1,0.24],[0,0.6,0.6],[0,0.24,1]],
[[0.24,1,0],[0,0.6,0],[0,0,0.6],[0.24,0,1]],
[[0.68,1,0],[0.6,0.6,0],[0.6,0,0],[0.6,0,0.6],[0.68,0,1]],
[[1,1,0],[1,0.68,0],[1,0.24,0],[1,0,0.24],[1,0,0.68],[1,0,1]]
];
By standard, I mean it should be affine transformed to meet the corner
position, edge directions and rounding extension. So, to round a given
corner with coordinates P0 and edge directions d1, d2 and d3 with an
extension r, the CPs of the rounded corner are computed by:
v1 = rd1/norm(d1);
v2 = rd2/norm(d2);
v3 = r*d3/norm(d3);
T = [ v1, v2, v3 ];
CP = [for(cpi=Q) [for(cpij=cpi) P0 + cpij*T ] ] ;
This tripatch is G2 and it meets the condition of geometric continuity of
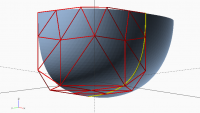
first and second derivatives. Here is an image of that tripatch meeting its
mirror transform for a corner at the origin and edges along the axis.
[image: G2corner.PNG]
In the image, the joint curve is represented in yellow.
Thanks to the standard tripatch, we could round all the corners of some
polyhedra other than cubes. Here is an example of its application to a
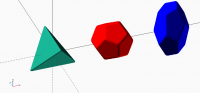
tetrahedron, a dodecahedron and a slanted dodecahedron.
[image: G2polyhedra.PNG]
In the computation of the standard control points, two form factors may be
arbitrated by the caller, one of them being the form factor of the 4th
degree curve which is the joint curve of the patches. The computation
implies the solution of a linear system of 6 equations for each pair of
form factors. The logic behind that computation is, as I said, a bit
technical. I may disclose the code that does the computation if someone is
interested in but be aware that, although it is fully commented, it is not
easily understandable without the technical fundamentals.