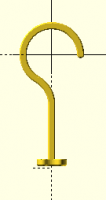
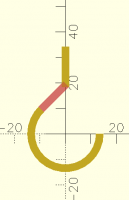
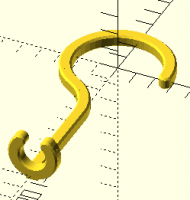
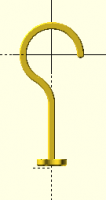
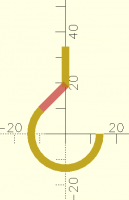
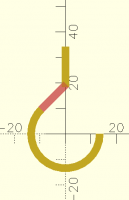
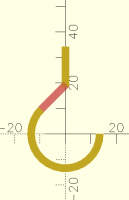
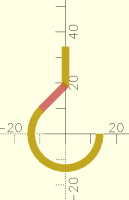
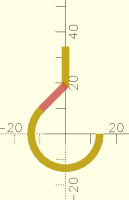
How can I connect these two pieces?
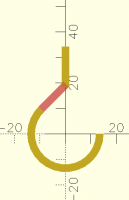
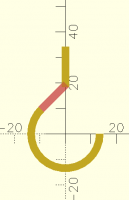
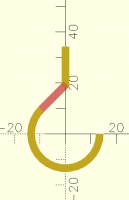
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
[image: image.png]
--
Mark Harrison
marhar@gmail.com
It is a tangent from a point to a circle.
https://en.wikipedia.org/wiki/Tangent_lines_to_circles
On Fri, 7 Mar 2025 at 20:07, Mark Harrison via Discuss <
discuss@lists.openscad.org> wrote:
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
[image: image.png]
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Probably best to work with points, and generate the polygon for the mid
section. You know the rh point at bottom of top piece ((3/2, 18.25) you
can use trig (sin & cos) to get the inner point of the 45 degree cut.
You can calculate the length of the middle section, (Pythagoras?) and
the width will be 3. You can generate the four points for the middle
rectangle (or a square based on the calculated length and 3) and
calculate its position. ( you have already found the two points needed.
(atan2 and translate). You do not need the lh, bottom point of the upper
piece, (-3/2,18.25) since if you use that you will get a tapered middle
section, unless you do another calculation to get one of the corners of
the middle piece.
You could write a generic script, where you enter the width and radius
and length of straight section, and produce the shape in whatever size
you want, merely by adjusting those three values. (or set the width and
length as a function of the radius, and then you only need to enter the
radius)
On 07/03/2025 20:06, Mark Harrison via Discuss wrote:
Here is a hook with a lower curved part and an upper straight part.
How can I calculate the proper dimension/position of the middle
connecting part? In this sample I visually positioned it by trial and
error, but I would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general
solution/principle as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
image.png
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
On 3/7/2025 12:06 PM, Mark Harrison via Discuss wrote:
Here is a hook with a lower curved part and an upper straight part.
How can I calculate the proper dimension/position of the middle
connecting part? In this sample I visually positioned it by trial and
error, but I would like to learn how to calculate this.
[...]
image.png
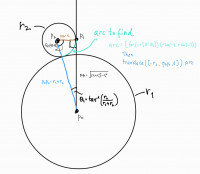
Mostly the answer is "math". (Which I know isn't all that helpful.)
Also: do you really want to connect the yellow segments, or do you
really want to position the vertical yellow segment so that it starts at
the point where a straight line from the curve meets the centerline?
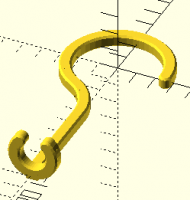
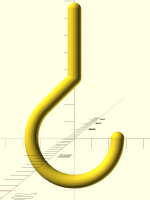
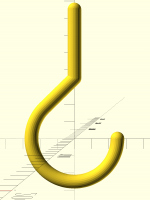
As it happens, I did exactly this a couple of years ago. It looks like
I was planning to put it on Thingiverse but never got around to it,
because I commented extensively on the math involved, complete with
diagrams... though it looks like I didn't really re-read it, because
I'm not following it all that well today. In particular, it doesn't
have an overall diagram of the object being created. Ah well, take a
look, and if you need explanation we can figure it out together.
Here's what I was building:
And here's the program. Note that the bottom part, pipe_polygon, is a
generic-ish sweep-oid module that would perhaps be better replaced by a
real sweep.
// Camelbak hook
inch = 25.4; // Let's work in inches.
$fn=30;
// pipe_d is the desired diameter of the "pipe" that
// the hook is made of. However, we want the side-to-side
// distance, and OpenSCAD's regular polygons are measured
// vertex to vertex. adj(d,sides) gives the vertex-to-vertex
// distance for a particular side-to-side distance and
// number of sides. (For even numbers of sides.)
pipe_d = 0.25inch;
pipe_r = pipe_d/2;
function adj(d, sides) = d/cos(360/sides/2);
pipe_bev = .3pipe_r;
d = 2*inch; // Diameter of the hook
r = d/2; // Radius of the hook
// Inside diameter of the hose loop. Measured from a
// real Camelbak hook.
// d2 is the diameter to the centerline of the pipe.
// r2 is the radius to the centerline of the pipe.
id = 0.54inch;
d2 = id + 2pipe_d/2;
r2 = d2/2;
// Length of the vertical segment after we finis
// the curves of the hook.
vertical = 2*inch;
// Build the body of the hook. I got obsessive and
// did the trig, but for the first draft I just tweaked
// the values until it looked right. Doing the trig
// does make it so you can tweak the angle as desired.
//
// The reverse curve to get from the loop back to the
// shaft is symmetric with the last part of the loop
// curve. a is the angle; it's the number
// of degrees we turn past vertical, and then it's the
// number of degrees we turn to get back to vertical.
// We calculate the straight segment required between the
// two arcs.
// Legal values for a range from >0 to 60. At zero the
// straight segment is infinite; at 60 it is zero and the
// two curves meet.
a = 60;
// The first 180 degrees is easy, and then we go another
// a degrees to complete the loop.
poly11 = circle(r, n=30, a=180+a);
// ... which ends at poly11end.
//
// Here's a diagram illustrating the trig that gets us there.
//
// Here's the first half of the curve:
// [-r, 0] [0,0]
// | |
// v v
// r
// .................
// . | (a .
// . | .
// . | .
// . | . r
// .
//
// ^
// |
// poly11end
//
// Considering the right triangle between the [0,0], the end
// point, and the cross-point above the end point, and remembering
// that cosine is the adjacent side over the hypotenuse, the
// x-distance between [0,0] and the end point is rcos(a).
// (The x-distance between the start point and the end point is r
// minus that, or either r-rcos(a) or r*(1-cos(a)). We don't need
// that yet, but we will.)
// Remembering that sine is opposite over hypotenuse, the
// y-distance between the start and the end (the length of
// the vertical bar) is rsin(a).
poly11end = [-rcos(a), -rsin(a)];
// Poly12 is the reverse curve (and the connection between
// poly11 and poly12 is the straight segment. We know we
// want the reverse curve to end at x=0, and so remembering
// that this curve is symmetric with the curve above, and
// remembering the x-distance between the start and end of that
// curve, it starts at x = -r(1-cos(a)).
//
// Now, what's the y distance between the poly11end and poly12start?
// Here's another diagram:
//
// .
// ..
// .a.
// . .
// . .
// y. .
// . .
// . .
// . . . . .
// x
//
// We know that the total x-distance between the start of the first
// curve and the end of the reverse curve is r. We know that the
// x-distance for each curve is r*(1-cos(a)). Thus the remaining
// x-distance that the straight segment must cover, x in the diagram
// above, is r-2r(1-cos(a)).
// Remembering that tangent is opposite over adjacent, or in this
// diagram x/y, and that we have x and want y, tan(a)=x/y, ytan(a)=x,
// y = x/tan(a). Thus the y-distance of the straight segment is
// (r-2r*(1-cos(a)))/tan(a). We add that to the end of the previous
// curve to get the start of the reverse curve.
// (We don't actually use p12start.x, but what the heck, let's be
// complete.)
poly12start = [-r*(1-cos(a)), poly11end.y - (r-2r(1-cos(a)))/tan(a)];
// We know that the reverse curve ends at x=0, and we know that the
// y-distance of one of these curves is rsin(a), so here's the end
// point of the reverse curve.
poly12end = [0, poly12start.y - rsin(a)];
// But... the circular arcs have their origin at the center of the
// circle, so we need to offset by r.
center12 = poly12end - [r, 0];
poly12 = translate(circle(r, n=30, a=-a, start=a), center12);
// And add on the vertical segment to reach the end point.
p13 = poly12end - [0, vertical];
poly13 = [p13];
// Here's the full line of the body of the hook: The initial
// counter-clockwise curve, the clockwise curve to get back to
// vertical, and the final vertical segment.
poly1 = concat(poly11, poly12, poly13);
// To use cylinder-oid pipes, remove the polygon() and add
// d=adj(pipe_d, 8) and fnz=8.
pipe_polygon(poly=poly1, open=true) {
polygon([
[0,pipe_r],
[pipe_r - pipe_bev,pipe_r],
[pipe_r, pipe_r - pipe_bev],
[pipe_r,-(pipe_r - pipe_bev)],
[pipe_r - pipe_bev,-pipe_r],
[0,-pipe_r]]);
};
// Now let's build the loop that holds the CamelBak tube.
// Experimentally, 270 degrees seems to be enough to grab the
// tube, while keeping the opening wide enough to push the
// tube through.
//
// Best is if you push the tube through the opening and then
// slide the hook up over the fitting at the bladder where
// it's thicker.
poly21 = circle(r2, n=30, start=135, a=270);
translate(p13) {
rotate([90,0,0])
translate([0,r2,0]) // get the bottom of the loop to [0,0]
// To use cylinder-oid pipes, remove the polygon() and add
// d=adj(pipe_d, 8) and fnz=8.
pipe_polygon(poly=poly21, open=true) {
polygon([
[0,pipe_r],
[pipe_r - pipe_bev,pipe_r],
[pipe_r, pipe_r - pipe_bev],
[pipe_r,-(pipe_r - pipe_bev)],
[pipe_r - pipe_bev,-pipe_r],
[0,-pipe_r]]);
}
// I was having problems with bed adhesion at this joint.
// This block gives it just a bit more bed contact.
translate([-pipe_d/2, -pipe_d/2, -pipe_d/2])
cube([pipe_d, pipe_d, pipe_d/2]);
}
// Given a series of points, connect them with a pipe.
// This module has more features than are used in this model.
// poly - the array of points.
// r, d - the radius or diameter of the pipe. (NB this is the OpenSCAD
// distance, measured to the vertices.)
// fill - if true, fill the interior of the figure, yielding a
// filled polygon with rounded edges. (Requires open=false.)
// open - if false, connect the start and end points to close
// the polygon.
// round_ends - if true, cap the ends with spheres.
// fnz - the $fn value to use for the cylinder and the z-curves at the
// corners. This lets you make pipes with polygonal cross-sections.
// Note that $fa, $fs, and $fn control the smoothness at corners.
module pipe_polygon(poly, r, d, fill=false, open=false, round_ends=true, fnz=$fn) {
_r = default(r, default(d,1)/2);
for (i = [(round_ends ? 0 : 1) : len(poly)-(round_ends ? 1 : 2)]) {
p = poly[i];
translate([p[0], p[1], 0]) {
// children() always yields one (possibly empty)
// object, and so if we try to pass it to corner
// then corner can't tell whether a child was really
// supplied.
if ($children == 0) {
corner(r=_r, fnz=fnz);
} else {
corner(r=_r, fnz=fnz)
children();
}
}
}
poly2 = open ? poly : concat(poly, [poly[0]]);
for (i=[0:len(poly2)-2]) {
p1 = poly2[i];
p2 = poly2[i+1];
dy = p2[1] - p1[1];
dx = p2[0] - p1[0];
translate([p1[0], p1[1], 0]) {
rotate([0,90,atan2(dy, dx)])
if ($children == 0) {
rotate([0,0,360/fnz/2])
cylinder(r=_r, h=norm([dx, dy]), $fn=fnz);
} else {
linear_extrude(height=norm([dx,dy])) {
union() {
children();
mirror([1,0,0]) children();
}
}
}
}
}
if (fill) linear_extrude(_r*2, center=true) polygon(poly);
// corner() defaults to a slice of a spheroid. It's done
// this way so that it can have different smoothing in x-y
// and z, so that it can mate with a polygonal pipe.
module corner(r, a, fnz) {
rotate_extrude(angle=a) {
if ($children == 0) {
intersection() {
rotate([0,0,360/fnz/2])
circle(r=r, $fn=fnz);
translate([0,-r*2])
square([r*2, r*4]);
}
} else {
children();
}
}
}
}
function default(v, def) = (v == undef) ? def : v;
function circle(r, n, a, start=0) = [ for (i=[0:n]) r*[cos(start+ia/n), sin(start+ia/n)]];
function translate(list, off) = [ for (p=list) p+off ];
Very nice take, Jordan. The other way that this can be done is using
BOSL2's NURBS library. If I recall correctly, you can use a triangle or
square control of control points, and set the weight of those vertices to
sqrt(2)/2, and you can represent an exact circle or arc. I do not have
time at the moment to code this up, but maybe someone experienced with
NURBS could wack an example together.
EBo --
On Fri, Mar 7, 2025 at 7:33 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
On 3/7/2025 12:06 PM, Mark Harrison via Discuss wrote:
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
[...]
[image: image.png]
Mostly the answer is "math". (Which I know isn't all that helpful.)
Also: do you really want to connect the yellow segments, or do you really
want to position the vertical yellow segment so that it starts at the point
where a straight line from the curve meets the centerline?
As it happens, I did exactly this a couple of years ago. It looks like I
was planning to put it on Thingiverse but never got around to it, because I
commented extensively on the math involved, complete with diagrams...
though it looks like I didn't really re-read it, because I'm not
following it all that well today. In particular, it doesn't have an
overall diagram of the object being created. Ah well, take a look, and if
you need explanation we can figure it out together.
Here's what I was building:
And here's the program. Note that the bottom part, pipe_polygon, is a
generic-ish sweep-oid module that would perhaps be better replaced by a
real sweep.
// Camelbak hook
inch = 25.4; // Let's work in inches.
$fn=30;
// pipe_d is the desired diameter of the "pipe" that
// the hook is made of. However, we want the side-to-side
// distance, and OpenSCAD's regular polygons are measured
// vertex to vertex. adj(d,sides) gives the vertex-to-vertex
// distance for a particular side-to-side distance and
// number of sides. (For even numbers of sides.)
pipe_d = 0.25inch;
pipe_r = pipe_d/2;
function adj(d, sides) = d/cos(360/sides/2);
pipe_bev = .3pipe_r;
d = 2*inch; // Diameter of the hook
r = d/2; // Radius of the hook
// Inside diameter of the hose loop. Measured from a
// real Camelbak hook.
// d2 is the diameter to the centerline of the pipe.
// r2 is the radius to the centerline of the pipe.
id = 0.54inch;
d2 = id + 2pipe_d/2;
r2 = d2/2;
// Length of the vertical segment after we finis
// the curves of the hook.
vertical = 2*inch;
// Build the body of the hook. I got obsessive and
// did the trig, but for the first draft I just tweaked
// the values until it looked right. Doing the trig
// does make it so you can tweak the angle as desired.
//
// The reverse curve to get from the loop back to the
// shaft is symmetric with the last part of the loop
// curve. a is the angle; it's the number
// of degrees we turn past vertical, and then it's the
// number of degrees we turn to get back to vertical.
// We calculate the straight segment required between the
// two arcs.
// Legal values for a range from >0 to 60. At zero the
// straight segment is infinite; at 60 it is zero and the
// two curves meet.
a = 60;
// The first 180 degrees is easy, and then we go another
// a degrees to complete the loop.
poly11 = circle(r, n=30, a=180+a);
// ... which ends at poly11end.
//
// Here's a diagram illustrating the trig that gets us there.
//
// Here's the first half of the curve:
// [-r, 0] [0,0]
// | |
// v v
// r
// .................
// . | (a .
// . | .
// . | .
// . | . r
// .
//
// ^
// |
// poly11end
//
// Considering the right triangle between the [0,0], the end
// point, and the cross-point above the end point, and remembering
// that cosine is the adjacent side over the hypotenuse, the
// x-distance between [0,0] and the end point is rcos(a).
// (The x-distance between the start point and the end point is r
// minus that, or either r-rcos(a) or r*(1-cos(a)). We don't need
// that yet, but we will.)
// Remembering that sine is opposite over hypotenuse, the
// y-distance between the start and the end (the length of
// the vertical bar) is rsin(a).
poly11end = [-rcos(a), -rsin(a)];
// Poly12 is the reverse curve (and the connection between
// poly11 and poly12 is the straight segment. We know we
// want the reverse curve to end at x=0, and so remembering
// that this curve is symmetric with the curve above, and
// remembering the x-distance between the start and end of that
// curve, it starts at x = -r(1-cos(a)).
//
// Now, what's the y distance between the poly11end and poly12start?
// Here's another diagram:
//
// .
// ..
// .a.
// . .
// . .
// y. .
// . .
// . .
// . . . . .
// x
//
// We know that the total x-distance between the start of the first
// curve and the end of the reverse curve is r. We know that the
// x-distance for each curve is r*(1-cos(a)). Thus the remaining
// x-distance that the straight segment must cover, x in the diagram
// above, is r-2r(1-cos(a)).
// Remembering that tangent is opposite over adjacent, or in this
// diagram x/y, and that we have x and want y, tan(a)=x/y, ytan(a)=x,
// y = x/tan(a). Thus the y-distance of the straight segment is
// (r-2r*(1-cos(a)))/tan(a). We add that to the end of the previous
// curve to get the start of the reverse curve.
// (We don't actually use p12start.x, but what the heck, let's be
// complete.)
poly12start = [-r*(1-cos(a)), poly11end.y - (r-2r(1-cos(a)))/tan(a)];
// We know that the reverse curve ends at x=0, and we know that the
// y-distance of one of these curves is rsin(a), so here's the end
// point of the reverse curve.
poly12end = [0, poly12start.y - rsin(a)];
// But... the circular arcs have their origin at the center of the
// circle, so we need to offset by r.
center12 = poly12end - [r, 0];
poly12 = translate(circle(r, n=30, a=-a, start=a), center12);
// And add on the vertical segment to reach the end point.
p13 = poly12end - [0, vertical];
poly13 = [p13];
// Here's the full line of the body of the hook: The initial
// counter-clockwise curve, the clockwise curve to get back to
// vertical, and the final vertical segment.
poly1 = concat(poly11, poly12, poly13);
// To use cylinder-oid pipes, remove the polygon() and add
// d=adj(pipe_d, 8) and fnz=8.
pipe_polygon(poly=poly1, open=true) {
polygon([
[0,pipe_r],
[pipe_r - pipe_bev,pipe_r],
[pipe_r, pipe_r - pipe_bev],
[pipe_r,-(pipe_r - pipe_bev)],
[pipe_r - pipe_bev,-pipe_r],
[0,-pipe_r]]);
};
// Now let's build the loop that holds the CamelBak tube.
// Experimentally, 270 degrees seems to be enough to grab the
// tube, while keeping the opening wide enough to push the
// tube through.
//
// Best is if you push the tube through the opening and then
// slide the hook up over the fitting at the bladder where
// it's thicker.
poly21 = circle(r2, n=30, start=135, a=270);
translate(p13) {
rotate([90,0,0])
translate([0,r2,0]) // get the bottom of the loop to [0,0]
// To use cylinder-oid pipes, remove the polygon() and add
// d=adj(pipe_d, 8) and fnz=8.
pipe_polygon(poly=poly21, open=true) {
polygon([
[0,pipe_r],
[pipe_r - pipe_bev,pipe_r],
[pipe_r, pipe_r - pipe_bev],
[pipe_r,-(pipe_r - pipe_bev)],
[pipe_r - pipe_bev,-pipe_r],
[0,-pipe_r]]);
}
// I was having problems with bed adhesion at this joint.
// This block gives it just a bit more bed contact.
translate([-pipe_d/2, -pipe_d/2, -pipe_d/2])
cube([pipe_d, pipe_d, pipe_d/2]);
}
// Given a series of points, connect them with a pipe.
// This module has more features than are used in this model.
// poly - the array of points.
// r, d - the radius or diameter of the pipe. (NB this is the OpenSCAD
// distance, measured to the vertices.)
// fill - if true, fill the interior of the figure, yielding a
// filled polygon with rounded edges. (Requires open=false.)
// open - if false, connect the start and end points to close
// the polygon.
// round_ends - if true, cap the ends with spheres.
// fnz - the $fn value to use for the cylinder and the z-curves at the
// corners. This lets you make pipes with polygonal cross-sections.
// Note that $fa, $fs, and $fn control the smoothness at corners.
module pipe_polygon(poly, r, d, fill=false, open=false, round_ends=true, fnz=$fn) {
_r = default(r, default(d,1)/2);
for (i = [(round_ends ? 0 : 1) : len(poly)-(round_ends ? 1 : 2)]) {
p = poly[i];
translate([p[0], p[1], 0]) {
// children() always yields one (possibly empty)
// object, and so if we try to pass it to corner
// then corner can't tell whether a child was really
// supplied.
if ($children == 0) {
corner(r=_r, fnz=fnz);
} else {
corner(r=_r, fnz=fnz)
children();
}
}
}
poly2 = open ? poly : concat(poly, [poly[0]]);
for (i=[0:len(poly2)-2]) {
p1 = poly2[i];
p2 = poly2[i+1];
dy = p2[1] - p1[1];
dx = p2[0] - p1[0];
translate([p1[0], p1[1], 0]) {
rotate([0,90,atan2(dy, dx)])
if ($children == 0) {
rotate([0,0,360/fnz/2])
cylinder(r=_r, h=norm([dx, dy]), $fn=fnz);
} else {
linear_extrude(height=norm([dx,dy])) {
union() {
children();
mirror([1,0,0]) children();
}
}
}
}
}
if (fill) linear_extrude(_r*2, center=true) polygon(poly);
// corner() defaults to a slice of a spheroid. It's done
// this way so that it can have different smoothing in x-y
// and z, so that it can mate with a polygonal pipe.
module corner(r, a, fnz) {
rotate_extrude(angle=a) {
if ($children == 0) {
intersection() {
rotate([0,0,360/fnz/2])
circle(r=r, $fn=fnz);
translate([0,-r*2])
square([r*2, r*4]);
}
} else {
children();
}
}
}
}
function default(v, def) = (v == undef) ? def : v;
function circle(r, n, a, start=0) = [ for (i=[0:n]) r*[cos(start+ia/n), sin(start+ia/n)]];
function translate(list, off) = [ for (p=list) p+off ];
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On Sat, 8 Mar 2025, 01:36 Mark Harrison via Discuss, <
discuss@lists.openscad.org> wrote:
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
[image: image.png]
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
My tip would be: Inkscape. With settings to mm you can design accurately,
either with stroke thickness, or (with Stroke to Path) a Path. This is an
old video where you can get an idea of the simplicity.
https://www.youtube.com/watch?v=JSu4j-EgjFc
Am Fr., 7. März 2025 um 21:07 Uhr schrieb Mark Harrison via Discuss <
discuss@lists.openscad.org>:
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
[image: image.png]
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I've ignored what has gone before, and have this, pretty well
parametric. Wrt a practical hook, then this design fails, it is merely
an example of stringing together a list of points to get a solid shape,
with some variation.
// Function to generate points on a circle's circumference
function pointcircle(d, a1, a2, s) = let(
radius = d / 2,
// Calculate the angular step and handle direction
angle_diff = (a2 - a1 + (a2 >= a1 ? 0 : 360)),
num_points = ceil(abs(angle_diff) / (360 / s))
) [for (i = [0 : num_points - 1])
let(angle = a1 + i * angle_diff / (num_points - 1))
[radius * cos(angle), radius * sin(angle), 0]
];
module pointshull(list){
for(k=[0:1:len(list)-2]){
hull(){
translate(list[k])sphere(w/2);
translate(list[k+1])sphere(w/2);
}
}
}
module shape(){
round=pointcircle(diam,sa,ea,res);
straight= [[0,es],[0,ss]];
all= concat(straight,round);
pointshull(all);
}
shape();
diam = 50; // diam of 'hook'
sa = 135; // start angle
ea = 0; // end angle
res = 200; // resolution for circle
ss = 35; // start of straight
w = 8; // diameter of 'wire'
es = ss+40; // end of straight
$fn = res/8;// smaller = quicker
If you want a square cross section, so you can easily fdm print, then do
it as 2d, and linear extrude. Using a $fn=4 or similar distorts the
cross section around the curve, since 'the cube' does not rotate as it
follows the path, so to speak.
On 07/03/2025 21:03, Raymond West via Discuss wrote:
Probably best to work with points, and generate the polygon for the
mid section. You know the rh point at bottom of top piece ((3/2,
18.25) you can use trig (sin & cos) to get the inner point of the 45
degree cut. You can calculate the length of the middle section,
(Pythagoras?) and the width will be 3. You can generate the four
points for the middle rectangle (or a square based on the calculated
length and 3) and calculate its position. ( you have already found the
two points needed. (atan2 and translate). You do not need the lh,
bottom point of the upper piece, (-3/2,18.25) since if you use that
you will get a tapered middle section, unless you do another
calculation to get one of the corners of the middle piece.
You could write a generic script, where you enter the width and radius
and length of straight section, and produce the shape in whatever size
you want, merely by adjusting those three values. (or set the width
and length as a function of the radius, and then you only need to
enter the radius)
On 07/03/2025 20:06, Mark Harrison via Discuss wrote:
Here is a hook with a lower curved part and an upper straight part.
How can I calculate the proper dimension/position of the middle
connecting part? In this sample I visually positioned it by trial
and error, but I would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general
solution/principle as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
image.png
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
Pythonscad path Extrude would be best Match. It has Lines and arcs in one
command and you can even define the Cross section.
Raymond West via Discuss discuss@lists.openscad.org schrieb am Sa., 8.
März 2025, 14:34:
I've ignored what has gone before, and have this, pretty well parametric.
Wrt a practical hook, then this design fails, it is merely an example of
stringing together a list of points to get a solid shape, with some
variation.
// Function to generate points on a circle's circumference
function pointcircle(d, a1, a2, s) = let(
radius = d / 2,
// Calculate the angular step and handle direction
angle_diff = (a2 - a1 + (a2 >= a1 ? 0 : 360)),
num_points = ceil(abs(angle_diff) / (360 / s))
) [for (i = [0 : num_points - 1])
let(angle = a1 + i * angle_diff / (num_points - 1))
[radius * cos(angle), radius * sin(angle), 0]
];
module pointshull(list){
for(k=[0:1:len(list)-2]){
hull(){
translate(list[k])sphere(w/2);
translate(list[k+1])sphere(w/2);
}
}
}
module shape(){
round=pointcircle(diam,sa,ea,res);
straight= [[0,es],[0,ss]];
all= concat(straight,round);
pointshull(all);
}
shape();
diam = 50; // diam of 'hook'
sa = 135; // start angle
ea = 0; // end angle
res = 200; // resolution for circle
ss = 35; // start of straight
w = 8; // diameter of 'wire'
es = ss+40; // end of straight
$fn = res/8;// smaller = quicker
If you want a square cross section, so you can easily fdm print, then do
it as 2d, and linear extrude. Using a $fn=4 or similar distorts the cross
section around the curve, since 'the cube' does not rotate as it follows
the path, so to speak.
On 07/03/2025 21:03, Raymond West via Discuss wrote:
Probably best to work with points, and generate the polygon for the mid
section. You know the rh point at bottom of top piece ((3/2, 18.25) you can
use trig (sin & cos) to get the inner point of the 45 degree cut. You can
calculate the length of the middle section, (Pythagoras?) and the width
will be 3. You can generate the four points for the middle rectangle (or a
square based on the calculated length and 3) and calculate its position. (
you have already found the two points needed. (atan2 and translate). You do
not need the lh, bottom point of the upper piece, (-3/2,18.25) since if you
use that you will get a tapered middle section, unless you do another
calculation to get one of the corners of the middle piece.
You could write a generic script, where you enter the width and radius and
length of straight section, and produce the shape in whatever size you
want, merely by adjusting those three values. (or set the width and length
as a function of the radius, and then you only need to enter the radius)
On 07/03/2025 20:06, Mark Harrison via Discuss wrote:
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
[image: image.png]
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I had the impression that the poster wanted the math, not an answer....but
BOSL2's turtle command also has lines and arcs in one command. You can
pass the result to path_sweep with the profile of your choice.
include<BOSL2/std.scad>
r=15;
stem=25;
angle=45;
path = turtle(["right", 90,
"arcright", r, 180+angle,
"untilx", 0,
"left", angle,
// "arcleft", 9, angle,
"move", stem], [r,0]);
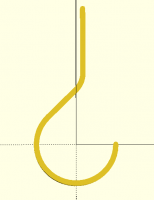
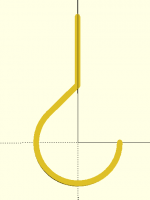
stroke(path,width=2);
It's easy to eliminate the sharp corner, though it does misalign the stem
with the center of the hook circle.
[image: image.png]
[image: image.png]
On Sat, Mar 8, 2025 at 8:40 AM Guenther Sohler via Discuss <
discuss@lists.openscad.org> wrote:
Pythonscad path Extrude would be best Match. It has Lines and arcs in one
command and you can even define the Cross section.
Raymond West via Discuss discuss@lists.openscad.org schrieb am Sa., 8.
März 2025, 14:34:
I've ignored what has gone before, and have this, pretty well parametric.
Wrt a practical hook, then this design fails, it is merely an example of
stringing together a list of points to get a solid shape, with some
variation.
// Function to generate points on a circle's circumference
function pointcircle(d, a1, a2, s) = let(
radius = d / 2,
// Calculate the angular step and handle direction
angle_diff = (a2 - a1 + (a2 >= a1 ? 0 : 360)),
num_points = ceil(abs(angle_diff) / (360 / s))
) [for (i = [0 : num_points - 1])
let(angle = a1 + i * angle_diff / (num_points - 1))
[radius * cos(angle), radius * sin(angle), 0]
];
module pointshull(list){
for(k=[0:1:len(list)-2]){
hull(){
translate(list[k])sphere(w/2);
translate(list[k+1])sphere(w/2);
}
}
}
module shape(){
round=pointcircle(diam,sa,ea,res);
straight= [[0,es],[0,ss]];
all= concat(straight,round);
pointshull(all);
}
shape();
diam = 50; // diam of 'hook'
sa = 135; // start angle
ea = 0; // end angle
res = 200; // resolution for circle
ss = 35; // start of straight
w = 8; // diameter of 'wire'
es = ss+40; // end of straight
$fn = res/8;// smaller = quicker
If you want a square cross section, so you can easily fdm print, then do
it as 2d, and linear extrude. Using a $fn=4 or similar distorts the cross
section around the curve, since 'the cube' does not rotate as it follows
the path, so to speak.
On 07/03/2025 21:03, Raymond West via Discuss wrote:
Probably best to work with points, and generate the polygon for the mid
section. You know the rh point at bottom of top piece ((3/2, 18.25) you can
use trig (sin & cos) to get the inner point of the 45 degree cut. You can
calculate the length of the middle section, (Pythagoras?) and the width
will be 3. You can generate the four points for the middle rectangle (or a
square based on the calculated length and 3) and calculate its position. (
you have already found the two points needed. (atan2 and translate). You do
not need the lh, bottom point of the upper piece, (-3/2,18.25) since if you
use that you will get a tapered middle section, unless you do another
calculation to get one of the corners of the middle piece.
You could write a generic script, where you enter the width and radius
and length of straight section, and produce the shape in whatever size you
want, merely by adjusting those three values. (or set the width and length
as a function of the radius, and then you only need to enter the radius)
On 07/03/2025 20:06, Mark Harrison via Discuss wrote:
Here is a hook with a lower curved part and an upper straight part. How
can I calculate the proper dimension/position of the middle connecting
part? In this sample I visually positioned it by trial and error, but I
would like to learn how to calculate this.
Pure SCAD, or a pointer to other code that might solve the geometry
appreciated. I am as interested in learning the general solution/principle
as I am in the practical solution to the problem.
// looped lower portion of hook
difference() {
circle(d=30);
circle(d=24);
square(30);
rotate(45) square(30);
}
// visually drawn mid-portion of hook
#rotate(45) translate([0,12]) square([14,3]);
// straight upper portion of hook
translate([-3/2,18.25]) square([3,16]);
[image: image.png]
--
Mark Harrison
marhar@gmail.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org