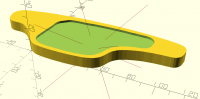
help with design approach
Looking at it carefully, I'll bet that a cylindrical wrap would
suffice. Can you point me to a way to do that with BOSL2?
I take my original set of points and smooth them with "offset(-5)
offset(5)", but the result is no longer accepted as input to
path_extrude2d(): are there BOSL2 library functions to smooth my point
list while still allowing the result to be used by path_extrude2d()?
Thank you!
Jon
On 5/11/2024 12:17 PM, Adrian Mariano via Discuss wrote:
Taking a flat object and mapping it to a sphere is not a well-defined
operation. BOSL2 does not provide a feature like this. It can wrap
things around cylinders, but that is a well-defined process. Think
about the problem of map projections. If you want to map an object
to there sphere there will be multiple ways to do it depending on how
you distort your object in the mapping.
But if you want to try the easiest thing and if you have your data as
points you can put it onto a sphere directly by computing z
coordinates that are on the sphere. The simplest scheme would be to
just project it along the z axis onto a sphere, e.g. using the formula
z_warped = sqrt(r^2-x^2-y^2)+z.
You can probably warp the lip this way if you make it using path_sweep
and get the VNF out and then warp the points component of the VNF.
(The faces won't change.)
On Sat, May 11, 2024 at 10:41 AM jon jonbondy.com
http://jonbondy.com via Discuss discuss@lists.openscad.org wrote:
You will notice that the object in the STL in the previous message
is actually not flat: it appears to be wrapped around the surface
of a fairly large sphere (diameter 10" or 20"?).
Are there any BOSL2 facilities that would take an object and warp
it in this manner? Since I have explicit 2D points lists, all I
would really need to do is add a 3rd dimension I suppose.
This is what I have at the moment:
Then there is the question of how to make a shape with rounded
edges that is also curved in this way (onto the sphere).
Jon
On 5/11/2024 10:29 AM, Jon Bondy via Discuss wrote:
Maybe this non-manifold STL will help everyone envision the shape
better.
On 5/11/2024 8:42 AM, Adrian Mariano via Discuss wrote:
Perhaps a better choice of glue could work?
I don't understand your problem at all from the description. To
me it sounds like your challenge is creating the "lips", but I
don't understand enough about the geometry to know how hard this
is. Like would sweeping a lip cross section along a planar
curve work? Or is the curve not planar (which creates twist
issues)? Or does the lip need to change across the sweep
because the shape it's mating to changes?
On Sat, May 11, 2024 at 8:24 AM Jon Bondy via Discuss
<discuss@lists.openscad.org> wrote:
Brainstorming, here...
I have a car with paddle shifters (thin, flat metal plates
with a curved
periphery). The car came with some paddle shifter
"extensions" which
sit behind the paddles (towards the front of the car, but
"behind" the
paddles from where I sit to drive). Think of the extensions
as flat
parts which are larger than the actual paddles, with a
paddle-shaped
indentation into which the paddles sit. They are only
attached with
glue, and one came off the day I bought the car (used). I
tried to
re-attach it with double-sided sticky tape, but that failed
after a few
weeks, so I am done with glue.
What I want to do is 1) design a part that is identical to
the original
extension and then 2) add flexible "lips" to go around the
paddle
shifter to hold the extension in place.
I can do (1) by photographing it and determining a series of
points to
specify the outer and inner shapes (1A). This is easy to do
approximately (and I have done so), but doing it accurately
would take
some time fiddling with the point list.
I could also do (1) by scanning the part (also done) (1B).
Although the above for (1) is a little challenging, the real
challenge
is how to create (2), the "lips" that wrap around the edge
of the
paddles to keep the extension in place. The lips must curve
around the
inner shape (the one that defines the outside of the
indentation).
I imagine that scanning (1B) will solve (1) but not help at
all with
(2). If I use the hand-crafted points approach (1B), then
at least I
have a defined curve around which I can sweep the lip
cross-section.
Any thoughts or comments?
Thanks!
Jon
--
This email has been checked for viruses by AVG antivirus
software.
www.avg.com <http://www.avg.com>
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
<http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient>
Virus-free.www.avg.com
<http://www.avg.com/email-signature?utm_medium=email&utm_source=link&utm_campaign=sig-email&utm_content=emailclient>
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
--
This email has been checked for viruses by AVG antivirus software.
www.avg.com