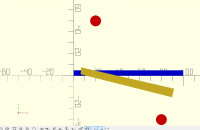
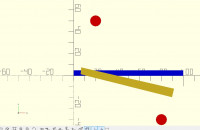
If considering 2d, (the sums are easier than 3d) if you have enough points in a polygon, you can manipulate them in whatever fashion you want. the blue is the original 'square'  (100 by 5) the yellow is a list of 96 points points on the edge of the 'square' manipulated by an inverse square of distance (sort of) from the two red points. If the same manipulation is applied to the original four points of the square, then the following less interesting shape is obtained. The manipulation is all within standard scad code, but the extra points are generated elsewhere. the values for the two points are  p1 = [20,50,30000];  p2 = [80,-40,30000]; where 300000 is a value to represent the 'strength' of influence' which is divided by the (distance of a point on the shape to the point of influence) squared to get the new point position, but it could be changed for other effects. On 02/09/2022 12:59, andrew goh via Discuss wrote: > _______________________________________________ > OpenSCAD mailing list > To unsubscribe send an email todiscuss-leave@lists.openscad.org

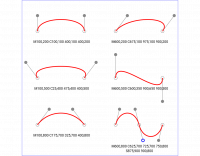
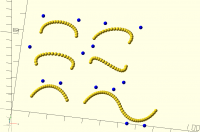
Thanks ! :) I tried reproducing cubic Bezier curves as given in W3C's specs for SVG https://www.w3.org/TR/SVG/paths.html#PathDataCubicBezierCommands <https://www.w3.org/TR/SVG/paths.html#PathDataCubicBezierCommands> The actual code is this: https://www.w3.org/TR/SVG/images/paths/cubic02.svg <https://www.w3.org/TR/SVG/images/paths/cubic02.svg> it looks like ths: w3c svg cubic bezier examples The openscad attempt looks like this: openscad cubic bezier attempt The point is if similar primitives can be provided say similar to the SVG specs. It would be easier to do things like this SVG to OpenSCAD Bezier extension for Inkscape https://www.thingiverse.com/thing:2805184 <https://www.thingiverse.com/thing:2805184> i.e. the curves (i.e. tuning of the control points) can be edited in Inkscape and 'imported' into OpenSCAD. While doing this attempt, I realized there is some 'secrets' for W3C's SVG cubic bezier curves. They are actually 'locally referenced' at the origin for the first control (end) point. The whole beizer curve is then translated with this first control point (which is the origin) to the desired position (i.e. the SVG coordinates for the 1st control point). if you used the true absolute coordinates, for the bezier calculations totally different Bezier curves are created. For now the Inkscape extension i'd guess works, I've not tried it out really. But that having a similar implementation makes it easier to integrate the 'graphical' front end apps, with other inkscape scripts. It'd certainly be more difficult I'd guess for Bezier surfaces Cheers,   Andrew I've added the openscad script for making these Bezier curves at the end of the message. On 02/09/2022 22:18, Raymond West wrote: > > If considering 2d, (the sums are easier than 3d) if you have enough > points in a polygon, you can manipulate them in whatever fashion you > want. > > the blue is the original 'square'  (100 by 5) > > the yellow is a list of 96 points points on the edge of the 'square' > manipulated by an inverse square of distance (sort of) from the two > red points. > > If the same manipulation is applied to the original four points of the > square, then the following less interesting shape is obtained. > > The manipulation is all within standard scad code, but the extra > points are generated elsewhere. > > the values for the two points are  p1 = [20,50,30000];  p2 = > [80,-40,30000]; > where 300000 is a value to represent the 'strength' of influence'  > which is divided by the (distance of a point on the shape to the point > of influence) squared to get the new point position, but it could be > changed for other effects. > > > _______________________________________________ > OpenSCAD mailing list > To unsubscribe send an email todiscuss-leave@lists.openscad.org --- Openscad script to test out the cubic Beziers - an attempt to reproduce the W3C svg path figures: $fn = 20; // t : 0 <= t <= 1 function cubic_bezier(p0, p1, p2, p3, t) =   (1-pow(t,3))*p0 + 3*(1-t)*(1-t)*t*p1   + 3*(1-t)*t*t*p2 + t*t*t*p3; module draw_bezier(p0, p1, p2, p3) {     translate(p1)         color("blue")             sphere(r=1);     translate(p2)         color("blue")             sphere(r=1);     for(t=[0:5:100]) {         p = cubic_bezier(p0, p1, p2, p3, t/100.0);         //echo(p);         translate(p)             sphere(r=1);     } } module b1() { p0 = [0,0,0]; p1 = [0,10,0]; p2 = [20,10,0]; p3 = [20,0,0]; translate([10,50,0])     draw_bezier(p0, p1, p2, p3); } module b2() { p0 = [0,0,0]; p1 = [5,10,0]; p2 = [25,10,0]; p3 = [20,0,0]; translate([40,50,0])     draw_bezier(p0, p1, p2, p3); } module b3() { p0 = [0,0,0]; p1 = [-5,10,0]; p2 = [25,10,0]; p3 = [20,0,0]; translate([10,30,0])     draw_bezier(p0, p1, p2, p3); } module b4() { p0 = [0,0,0]; p1 = [0,10,0]; p2 = [20,-10,0]; p3 = [20,0,0]; translate([40,35,0])     draw_bezier(p0, p1, p2, p3); } module b5() { p0 = [0,0,0]; p1 = [5,10,0]; p2 = [15,10,0]; p3 = [20,0,0]; translate([10,10,0])     draw_bezier(p0, p1, p2, p3); } module b6() { p0 = [0,0,0]; p1 = [5,10,0]; p2 = [15,10,0]; p3 = [20,0,0]; translate([40,10,0])     draw_bezier(p0, p1, p2, p3); p4 = [0,0,0]; p5 = [5,-10,0]; p6 = [15,-10,0]; p7 = [20,0,0]; translate([60,10,0])     draw_bezier(p4, p5, p6, p7); } b1(); b2(); b3(); b4(); b5(); b6();