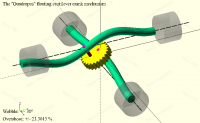
The first attempt had the rod as part of the floating cantilever crank to get the same precession as a sort of free ride, as I thought. It's all on the same line (in the vertical plane) with the pistons, as near as dammit. Well yes, but watching the ends of the rods, their wandering around the centreline was too conspicuous. I tried all sorts of remedies before it dawned on me that it was a second order, not a first order phenomenon. So it was going to need $t\*720. But it would have been fudge upon fudge, and anyway, in reality the pistons are constrained to move in a straight line, while the piston bearing is free to move axially on the crankpin – so, back to square one with a different frame of reference. While I was at it, I threw in a function to link the wobble angle to the deflection height. And I found that \*cos(i/2) gives very similar attenuation to the previous complex exponential thing. Thus was born the second attempt to be seen in the attached animation with a massive 30° wobble. The crankpins (not to scale!) riding up and down in the rods can be seen clearly, while the ends of the rods stay right on the centreline – whatever the angle of wobble. Having done that, I had another look at the Bezier curve suggested by Jordan Brown and rendered the three curves on top of each other (red=Bezier, blue=cos(i/2) attenuation, green=exponential attenuation – see script). It's remarkable how similar they are, but the Bezier curve best matches my idea of what the curve should look like with a bearing in the middle. Question: is there an equation for interconverting curve height and wobble angle (slope angle through the origin) to parametrise these and to ensure a precise match between rods and crankpins? The second attempt: `// 3 Beam deflections` `include <BOSL2/std.scad>` `include <BOSL2/beziers.scad>` `// Bezier rod` `bezpath = flatten([` `bez_begin([-450, 0], 0,150),` `bez_tang ([ 0, 0], 21.6*cos($t*360), 250), //centre xy, ~defl. height, ~max. defl. dist. from centre` `bez_end ([ 450, 0], 180,150),` `]);` `color("red")` `path_sweep(circle(d=4), bezpath_curve(bezpath));` `// Attenuated sine curves` `a = 34; // Wiggle factor, vertical (rod 1)` `w = 20; // Wobble, deg. (rod2)` `H = 2.5; // Rod slice length` `module rod1()` `color("limegreen")` `{` `sweep(circle(2, $fn=50), ` `[for (i=[-180:1:180])` `up(H*i) // Length` `* back(a*cos($t*360)*sin(i) * pow((pow(180, 2)-pow(i, 2)), 1.1)/pow(245, 2) )` `]);` `}` `module rod2()` `color("blue")` `{` `sweep(circle(2, $fn=50), ` `[for (i=[-180:1:180])` `up(H*i) // Length` `* back(woblht(H, w)*cos($t*360) * sin(i) * cos(i/2) )` `]);` `}` `function woblht (H, w) = tan(w) * H / sin(1);` `rotate([0, 90, 0])` `rod1();` `rotate([0, 90, 0])` `rod2();` `// Reference angle` `/*` `rotate([90, 0, 90-w*cos($t*360)])` `color("blue")` `cylinder(r=1, h=300, center=true);` `*/` `rotate([0, 90, 90+w*cos($t*360)])` `difference()` `{` `circle(70);` `circle(42);` `}` Sorry, no animation! What is the size limit for attachments?