The $fa/$fs calculation should be tweaked to always yield multiples of 4
Mostly, you want to use $fa and $fs and let OpenSCAD figure out the
number of sides that circles should have.
However, if you are trying to join a circle (or other circular shape) to
a rectangular shape, you probably want the vertices on the circle to
align with the vertices on the rectangle.
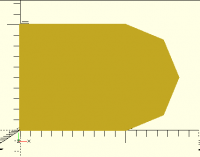
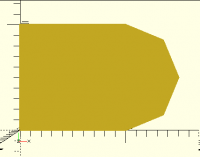
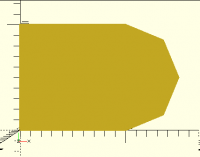
Here's a deliberately low-circular-resolution shape to demonstrate the
problem:
$fa = 10;
$fs = 5;
size = 10;
translate([size, size/2]) circle(d=size);
square(size);
With those parameters, the circle ends up a 7-gon, and doesn't mate well
with the square:
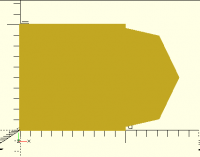
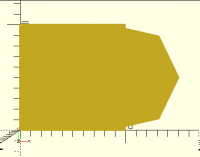
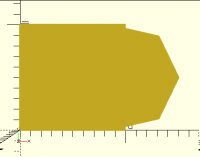
If we assume that nobody depends on $fa/$fs using exactly the current
formula, we could make it round up to a multiple of 4, turning the
circle above into an octagon:
... which mates a lot better. The same principle applies at any size.
If the result is not a multiple of 4, the circle won't mate well with a
rectangle; there will be a slight artifact at the join. Today, if you
want to avoid this artifact you have to set $fn explicitly, perhaps
calculating it from $fa and $fs and rounding.
It's a little hard to see anybody depending on the formula used for
$fa/$fs. If we were to round the result up to a multiple of four, a
bunch of artifacts would just go away without needing explicit
calculation in the model.
No scheme will make them mate well when the rectangular edge is at an
arbitrary angle, but multiple-of-four will make them mate well with
horizontal and vertical lines, and of course it'll stay good if you then
rotate the whole assembly. (Or if you're trying to match a rotated
line, and you rotate the circle the same way.)
Unfortunately, it's not inconceivable that somebody might depend on the
formula - in particular, to predict the shape of a circle and then
adjust geometry to match. (They'd probably be better off calculating
the equivalent $fn and using that explicitly, rather than trying to
match the results of the internal calculation, but...)
I think it's worth the small compatibility hiccup. What do others think?
It seems reasonable to me. Of course, it would break stuff in BOSL2 where
we want to ensure that we match things that users have made using $fa/$fs.
There's another thing, which is that I think if $fn is a multiple of 4 then
the circle actually reaches its advertised radius on the four axes, which
is also a desirable property.
On Thu, Sep 19, 2024 at 10:39 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
Mostly, you want to use $fa and $fs and let OpenSCAD figure out the number
of sides that circles should have.
However, if you are trying to join a circle (or other circular shape) to a
rectangular shape, you probably want the vertices on the circle to align
with the vertices on the rectangle.
Here's a deliberately low-circular-resolution shape to demonstrate the
problem:
$fa = 10;
$fs = 5;
size = 10;
translate([size, size/2]) circle(d=size);
square(size);
With those parameters, the circle ends up a 7-gon, and doesn't mate well
with the square:
If we assume that nobody depends on $fa/$fs using exactly the current
formula, we could make it round up to a multiple of 4, turning the circle
above into an octagon:
... which mates a lot better. The same principle applies at any size. If
the result is not a multiple of 4, the circle won't mate well with a
rectangle; there will be a slight artifact at the join. Today, if you want
to avoid this artifact you have to set $fn explicitly, perhaps calculating
it from $fa and $fs and rounding.
It's a little hard to see anybody depending on the formula used for
$fa/$fs. If we were to round the result up to a multiple of four, a bunch
of artifacts would just go away without needing explicit calculation in the
model.
No scheme will make them mate well when the rectangular edge is at an
arbitrary angle, but multiple-of-four will make them mate well with
horizontal and vertical lines, and of course it'll stay good if you then
rotate the whole assembly. (Or if you're trying to match a rotated line,
and you rotate the circle the same way.)
Unfortunately, it's not inconceivable that somebody might depend on the
formula - in particular, to predict the shape of a circle and then adjust
geometry to match. (They'd probably be better off calculating the
equivalent $fn and using that explicitly, rather than trying to match the
results of the internal calculation, but...)
I think it's worth the small compatibility hiccup. What do others think?
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I'm reasonably sure I've used $fn = 3 to make triangular prisms. I wouldn't
want this to break, directly or indirectly.
As an aside, I've just learned from the docs that the following is possible
to use two different values between previewing and rendering a model:
$fn = $preview ? 32 : 64;
Amazing stuff! Wish I'd learned that ten years ago. :D
On Fri, 20 Sept 2024 at 13:24, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
It seems reasonable to me. Of course, it would break stuff in BOSL2 where
we want to ensure that we match things that users have made using $fa/$fs.
There's another thing, which is that I think if $fn is a multiple of 4
then the circle actually reaches its advertised radius on the four axes,
which is also a desirable property.
On Thu, Sep 19, 2024 at 10:39 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
Mostly, you want to use $fa and $fs and let OpenSCAD figure out the
number of sides that circles should have.
However, if you are trying to join a circle (or other circular shape) to
a rectangular shape, you probably want the vertices on the circle to align
with the vertices on the rectangle.
Here's a deliberately low-circular-resolution shape to demonstrate the
problem:
$fa = 10;
$fs = 5;
size = 10;
translate([size, size/2]) circle(d=size);
square(size);
With those parameters, the circle ends up a 7-gon, and doesn't mate well
with the square:
If we assume that nobody depends on $fa/$fs using exactly the current
formula, we could make it round up to a multiple of 4, turning the circle
above into an octagon:
... which mates a lot better. The same principle applies at any size.
If the result is not a multiple of 4, the circle won't mate well with a
rectangle; there will be a slight artifact at the join. Today, if you want
to avoid this artifact you have to set $fn explicitly, perhaps calculating
it from $fa and $fs and rounding.
It's a little hard to see anybody depending on the formula used for
$fa/$fs. If we were to round the result up to a multiple of four, a bunch
of artifacts would just go away without needing explicit calculation in the
model.
No scheme will make them mate well when the rectangular edge is at an
arbitrary angle, but multiple-of-four will make them mate well with
horizontal and vertical lines, and of course it'll stay good if you then
rotate the whole assembly. (Or if you're trying to match a rotated line,
and you rotate the circle the same way.)
Unfortunately, it's not inconceivable that somebody might depend on the
formula - in particular, to predict the shape of a circle and then adjust
geometry to match. (They'd probably be better off calculating the
equivalent $fn and using that explicitly, rather than trying to match the
results of the internal calculation, but...)
I think it's worth the small compatibility hiccup. What do others think?
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
He's only suggesting changing $fa/$fs behavior, not explicit specification
with $fn where maybe you want a heptagon.
On Thu, Sep 19, 2024 at 11:40 PM tjhowse via Discuss <
discuss@lists.openscad.org> wrote:
I'm reasonably sure I've used $fn = 3 to make triangular prisms. I
wouldn't want this to break, directly or indirectly.
As an aside, I've just learned from the docs that the following is
possible to use two different values between previewing and rendering a
model:
$fn = $preview ? 32 : 64;
Amazing stuff! Wish I'd learned that ten years ago. :D
On Fri, 20 Sept 2024 at 13:24, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
It seems reasonable to me. Of course, it would break stuff in BOSL2
where we want to ensure that we match things that users have made using
$fa/$fs.
There's another thing, which is that I think if $fn is a multiple of 4
then the circle actually reaches its advertised radius on the four axes,
which is also a desirable property.
On Thu, Sep 19, 2024 at 10:39 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
Mostly, you want to use $fa and $fs and let OpenSCAD figure out the
number of sides that circles should have.
However, if you are trying to join a circle (or other circular shape) to
a rectangular shape, you probably want the vertices on the circle to align
with the vertices on the rectangle.
Here's a deliberately low-circular-resolution shape to demonstrate the
problem:
$fa = 10;
$fs = 5;
size = 10;
translate([size, size/2]) circle(d=size);
square(size);
With those parameters, the circle ends up a 7-gon, and doesn't mate well
with the square:
If we assume that nobody depends on $fa/$fs using exactly the current
formula, we could make it round up to a multiple of 4, turning the circle
above into an octagon:
... which mates a lot better. The same principle applies at any size.
If the result is not a multiple of 4, the circle won't mate well with a
rectangle; there will be a slight artifact at the join. Today, if you want
to avoid this artifact you have to set $fn explicitly, perhaps calculating
it from $fa and $fs and rounding.
It's a little hard to see anybody depending on the formula used for
$fa/$fs. If we were to round the result up to a multiple of four, a bunch
of artifacts would just go away without needing explicit calculation in the
model.
No scheme will make them mate well when the rectangular edge is at an
arbitrary angle, but multiple-of-four will make them mate well with
horizontal and vertical lines, and of course it'll stay good if you then
rotate the whole assembly. (Or if you're trying to match a rotated line,
and you rotate the circle the same way.)
Unfortunately, it's not inconceivable that somebody might depend on the
formula - in particular, to predict the shape of a circle and then adjust
geometry to match. (They'd probably be better off calculating the
equivalent $fn and using that explicitly, rather than trying to match the
results of the internal calculation, but...)
I think it's worth the small compatibility hiccup. What do others think?
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I just have a circle4n() module in my library and I have redefined sphere()
to use it.
On Fri, 20 Sept 2024 at 04:41, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
He's only suggesting changing $fa/$fs behavior, not explicit specification
with $fn where maybe you want a heptagon.
On Thu, Sep 19, 2024 at 11:40 PM tjhowse via Discuss <
discuss@lists.openscad.org> wrote:
I'm reasonably sure I've used $fn = 3 to make triangular prisms. I
wouldn't want this to break, directly or indirectly.
As an aside, I've just learned from the docs that the following is
possible to use two different values between previewing and rendering a
model:
$fn = $preview ? 32 : 64;
Amazing stuff! Wish I'd learned that ten years ago. :D
On Fri, 20 Sept 2024 at 13:24, Adrian Mariano via Discuss <
discuss@lists.openscad.org> wrote:
It seems reasonable to me. Of course, it would break stuff in BOSL2
where we want to ensure that we match things that users have made using
$fa/$fs.
There's another thing, which is that I think if $fn is a multiple of 4
then the circle actually reaches its advertised radius on the four axes,
which is also a desirable property.
On Thu, Sep 19, 2024 at 10:39 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
Mostly, you want to use $fa and $fs and let OpenSCAD figure out the
number of sides that circles should have.
However, if you are trying to join a circle (or other circular shape)
to a rectangular shape, you probably want the vertices on the circle to
align with the vertices on the rectangle.
Here's a deliberately low-circular-resolution shape to demonstrate the
problem:
$fa = 10;
$fs = 5;
size = 10;
translate([size, size/2]) circle(d=size);
square(size);
With those parameters, the circle ends up a 7-gon, and doesn't mate
well with the square:
If we assume that nobody depends on $fa/$fs using exactly the current
formula, we could make it round up to a multiple of 4, turning the circle
above into an octagon:
... which mates a lot better. The same principle applies at any size.
If the result is not a multiple of 4, the circle won't mate well with a
rectangle; there will be a slight artifact at the join. Today, if you want
to avoid this artifact you have to set $fn explicitly, perhaps calculating
it from $fa and $fs and rounding.
It's a little hard to see anybody depending on the formula used for
$fa/$fs. If we were to round the result up to a multiple of four, a bunch
of artifacts would just go away without needing explicit calculation in the
model.
No scheme will make them mate well when the rectangular edge is at an
arbitrary angle, but multiple-of-four will make them mate well with
horizontal and vertical lines, and of course it'll stay good if you then
rotate the whole assembly. (Or if you're trying to match a rotated line,
and you rotate the circle the same way.)
Unfortunately, it's not inconceivable that somebody might depend on the
formula - in particular, to predict the shape of a circle and then adjust
geometry to match. (They'd probably be better off calculating the
equivalent $fn and using that explicitly, rather than trying to match the
results of the internal calculation, but...)
I think it's worth the small compatibility hiccup. What do others
think?
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org