radius = 10;
fn = 18; // The shape

v1 = circv(radius, fn);
polygon(v1);

// create 2d vector shape: circle
function circv(r=1, fn=32) =
  [ for(i=[0 : fn-1]) [r*cos(360*i/fn),r*sin(360*i/fn)] ];

start = ... whatever start value ...;
end = ... whatever end value ...;
step = ... whatever step ...;
function f(i) = ... whatever generates your points, given i ...;
points = [
    for (i=[start:step:end]) f(i)
];
polygon(points);

    start = 0;
    end = 360;
    step = 1;
    function f(i) = [ cos(i), sin(i) ];
    points = [
        for (i=[start:step:end]) f(i)
    ];
    polygon(points);

points = [
    [0,0],
    for (i=[0:10]) [ i, i*i/10 + 1 ],
    [10, 0]
];
polygon(points);

points = [
    for (x=[0:360]) [ x, sin(x)*100+100 ],
    for (x=[360:-1:0])  [ x, sin(x)*100-100 ],
];
polygon(points);

There are any number of ways to put together a 2D figure, but you've found the right basic approach for the general case. On 3/26/2022 3:40 PM, Jan Öhman via Discuss wrote: > I found a tip (but I do not understand what happens and how to use it > in my case.) > > radius = 10; > fn = 18; // The shape > > v1 = circv(radius, fn); > dispv(v1); > > // create 2d vector shape: circle > function circv(r=1, fn=32) = >   [ for(i=[0 : fn-1]) [r*cos(360*i/fn),r*sin(360*i/fn)] ]; > > > // display a 2d vector shape > module dispv(v){ >   indi = [[for(i=[0 : len(v)-1])i]]; >   polygon(points=v, paths=indi); > } > This is more complex than is needed. Here's a simpler version of the same thing: radius = 10; fn = 18; // The shape v1 = circv(radius, fn); polygon(v1); // create 2d vector shape: circle function circv(r=1, fn=32) = [ for(i=[0 : fn-1]) [r*cos(360*i/fn),r*sin(360*i/fn)] ]; There are three interesting parts of this program: * Drawing a polygon.  Given a list of points, OpenSCAD will draw a polygon.  But how do you easily make a list of points from a formula? * List comprehension.  When you say something like list = [ for (i=[1:10]) i*i ]; echo(list); it builds a list by repeatedly evaluating the expression.  Try running that little program. There are several other variations on list comprehensions and they are useful in a wide variety of cases, but that's the basic one that you need for generating lists of points.  But what are the right values of the points? * Equation of a circle.  There are many ways to formulate the points for a circle.  Here the author is trying to generate an n-sided polygon.  They have i step from zero to one less than the number of vertices, and for each one they calculate an angle that splits the circle evenly - 360*i/fn.  Call that angle a.  The point [ r*cos(a), r*sin(a) ] is one point on that circle. Net, they're calculating successive points on a circle, putting them all in a list, and calling polygon() on the result. The general pattern is start = ... whatever start value ...; end = ... whatever end value ...; step = ... whatever step ...; function f(i) = ... 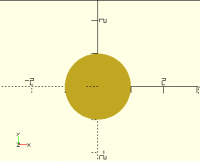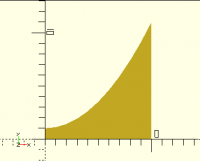whatever generates your points, given i ...; points = [ for (i=[start:step:end]) f(i) ]; polygon(points); So, for instance, this will generate a one-unit-radius circle (with far more sides than it needs): start = 0; end = 360; step = 1; function f(i) = [ cos(i), sin(i) ]; points = [ for (i=[start:step:end]) f(i) ]; polygon(points); Here's another example that is slightly more complex, adding a couple of fixed points: points = [ [0,0], for (i=[0:10]) [ i, i*i/10 + 1 ], [10, 0] ]; polygon(points); Note that you don't *need* to write the formula in the form of a function - do it if it makes it easier for you to understand. 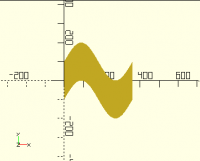You can get arbitrarily more complex - for instance: points = [ for (x=[0:360]) [ x, sin(x)*100+100 ], for (x=[360:-1:0]) [ x, sin(x)*100-100 ], ]; polygon(points);