Generating a helix with linear extrude
[ This was a math puzzle. It's almost certainly not the right way to
generate a helix. I thought others might find it interesting. ]
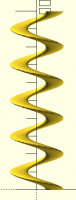
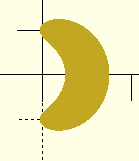
Everybody knows that you can't generate a helix with linear_extrude.
Linear extrude works with horizontal cross sections, and a proper helix
needs a circle (or whatever shape) that's tilted to perpendicular to the
angle of the helix. You end up with something like so:
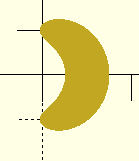
Some time back, I realized that you could generate a helix with linear
extrude. The problem is that the horizontal cross-section isn't
simple. It's sort of banana-shaped:
But what is that shape?
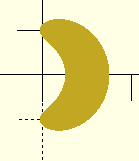
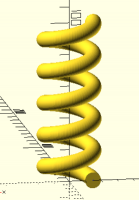
I got interested in this question again, and played with the idea that
it's a circle that's been stretched around the circumference of the helix.
I tried translating it into polar coordinates and scaling theta by
1/sin(helix angle), and although I'm not sure that it's absolutely
right, the result is pretty good:
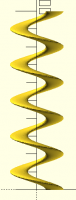
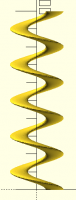
Here's a cross-section perpendicular to the helix angle:
Perfect circle? Maybe, maybe not. I'm not sure that I cut the
cross-section at exactly the right point, or took the screen shot from
the right angle.
Here's the demo program, intended for use with the customizer. The best
algorithm, A, is in bananaA(). bananaB() is a different way to stretch
the circle that doesn't really work, but I don't understand why not
because I can't think well in polar coordinates. circle() is a
straightforward circle, like you would get from the "doesn't work"
linear extrude solution. (And yes, of course if I was really trying to
write a helix function everything would be an argument, not a global.)
// Vertical distance from the centerline of one turn to the centerline of the next turn
pitch = 20;
// Radius of the helix, from XY=0 to the centerline of the extruded circle
helix_r = 15;
// Radius of the extruded circle
r = 5;
// Height of the helix
h = 100;
// Show cross-section (view from -Y orthogonal)
intersect = false;
// Which algorithm to use (a is best, b is interesting but not as good, 2 is simple circle)
algorithm = 0; // [ 0: a, 1: b, 2: circle ]
module stop();
// This is a little interesting to animate:
// pitch = 20 + 10abs($t2-1);
function torect2(p) = [
p[0] * cos(p[1]),
p[0] * sin(p[1])
];
function topolar2(p) = [
norm(p),
atan2(p.y, p.x)
];
// Helix angle
helix_a = atan2(pitch, helix_r2PI);
// degrees per unit, along the circumference
theta_scale = 360/(2PIhelix_r);
// Banana, algorithm A
bananaA = function() [
for (a=[0:359])
torect2([helix_r, 0] + [r*cos(a), r * sin(a) * theta_scale / sin(helix_a)])
];
// Banana, algorithm B
bananaB = function() [
for (a=[0:359])
let(circ = torect2([r, a])) // circle
let(tcirc = circ + [helix_r, 0]) // translated
let(pcirc = topolar2(tcirc)) // in polar coords
let(smeared_circ = [pcirc[0], pcirc[1]/sin(helix_a)])
torect2(smeared_circ)
];
// Simple circle, for comparison
circle = function() [
for (a=[0:359])
torect2([r, a]) + [helix_r, 0]
];
functions = [ bananaA, bananaB, circle ];
module helix() {
linear_extrude(height=h, twist=360*h/pitch, convexity=2)
polygon(functionsalgorithm);
}
if (intersect) {
intersection() {
#helix();
translate([helix_r, 0, pitch]) rotate([-helix_a,0,0]) cube([r2, 0.01, r2], center=true);
}
} else {
helix();
}
// A few reference shapes
// A circle. If helix_a is 90, this should match the bottom of the helix.
color("blue") translate([helix_r,0,-0.1]) linear_extrude(height=0.1) circle(r=r);
// The circumference of the helix.
color("green") translate([0,0,-0.2]) linear_extrude(height=0.1) difference() { circle(r=helix_r+0.1); circle(r=helix_r-0.1); }
Looks great
Probably you need to write a path extrude function.
I feel this should be part of regular openscad.
It wouldn't be too difficult to write this function, if you can write such
complex models.
On Tue, 27 Feb, 2024, 11:28 am Jordan Brown via Discuss, <
discuss@lists.openscad.org> wrote:
[ This was a math puzzle. It's almost certainly not the right way to
generate a helix. I thought others might find it interesting. ]
Everybody knows that you can't generate a helix with linear_extrude.
Linear extrude works with horizontal cross sections, and a proper helix
needs a circle (or whatever shape) that's tilted to perpendicular to the
angle of the helix. You end up with something like so:
Some time back, I realized that you could generate a helix with linear
extrude. The problem is that the horizontal cross-section isn't simple.
It's sort of banana-shaped:
But what is that shape?
I got interested in this question again, and played with the idea that
it's a circle that's been stretched around the circumference of the helix.
I tried translating it into polar coordinates and scaling theta by
1/sin(helix angle), and although I'm not sure that it's absolutely right,
the result is pretty good:
Here's a cross-section perpendicular to the helix angle:
Perfect circle? Maybe, maybe not. I'm not sure that I cut the
cross-section at exactly the right point, or took the screen shot from the
right angle.
Here's the demo program, intended for use with the customizer. The best
algorithm, A, is in bananaA(). bananaB() is a different way to stretch the
circle that doesn't really work, but I don't understand why not because I
can't think well in polar coordinates. circle() is a straightforward
circle, like you would get from the "doesn't work" linear extrude
solution. (And yes, of course if I was really trying to write a helix
function everything would be an argument, not a global.)
// Vertical distance from the centerline of one turn to the centerline of the next turn
pitch = 20;
// Radius of the helix, from XY=0 to the centerline of the extruded circle
helix_r = 15;
// Radius of the extruded circle
r = 5;
// Height of the helix
h = 100;
// Show cross-section (view from -Y orthogonal)
intersect = false;
// Which algorithm to use (a is best, b is interesting but not as good, 2 is simple circle)
algorithm = 0; // [ 0: a, 1: b, 2: circle ]
module stop();
// This is a little interesting to animate:
// pitch = 20 + 10abs($t2-1);
function torect2(p) = [
p[0] * cos(p[1]),
p[0] * sin(p[1])
];
function topolar2(p) = [
norm(p),
atan2(p.y, p.x)
];
// Helix angle
helix_a = atan2(pitch, helix_r2PI);
// degrees per unit, along the circumference
theta_scale = 360/(2PIhelix_r);
// Banana, algorithm A
bananaA = function() [
for (a=[0:359])
torect2([helix_r, 0] + [r*cos(a), r * sin(a) * theta_scale / sin(helix_a)])
];
// Banana, algorithm B
bananaB = function() [
for (a=[0:359])
let(circ = torect2([r, a])) // circle
let(tcirc = circ + [helix_r, 0]) // translated
let(pcirc = topolar2(tcirc)) // in polar coords
let(smeared_circ = [pcirc[0], pcirc[1]/sin(helix_a)])
torect2(smeared_circ)
];
// Simple circle, for comparison
circle = function() [
for (a=[0:359])
torect2([r, a]) + [helix_r, 0]
];
functions = [ bananaA, bananaB, circle ];
module helix() {
linear_extrude(height=h, twist=360*h/pitch, convexity=2)
polygon(functionsalgorithm);
}
if (intersect) {
intersection() {
#helix();
translate([helix_r, 0, pitch]) rotate([-helix_a,0,0]) cube([r2, 0.01, r2], center=true);
}
} else {
helix();
}
// A few reference shapes
// A circle. If helix_a is 90, this should match the bottom of the helix.
color("blue") translate([helix_r,0,-0.1]) linear_extrude(height=0.1) circle(r=r);
// The circumference of the helix.
color("green") translate([0,0,-0.2]) linear_extrude(height=0.1) difference() { circle(r=helix_r+0.1); circle(r=helix_r-0.1); }
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
another way to create helix purely in openscad
I wrote a function p_extrude (path extrude) in openscad but it may not work
in all cases. The function I wrote in python is much better as it is a
little simpler to code.
You would need dependencies.scad file where all the functions are written
include<dependencies.scad>
// helix function with parameters helix dia, pitch and number of turns
a=helix(30,20,5);
//module p_line3d to show the helix path
color("blue")p_line3d(a,.5,1);
// function circle to define points of circle with parameters radius,
center point and number of segments in circle
b=circle(5);
//function p_extrude with parameters section and path to extrude
c=p_extrude(b,a);
// module swp to create polyhedron
swp(c);
[image: image.png]
On Wed, 28 Feb 2024 at 16:34, Sanjeev Prabhakar sprabhakar2006@gmail.com
wrote:
Looks great
Probably you need to write a path extrude function.
I feel this should be part of regular openscad.
It wouldn't be too difficult to write this function, if you can write such
complex models.
On Tue, 27 Feb, 2024, 11:28 am Jordan Brown via Discuss, <
discuss@lists.openscad.org> wrote:
[ This was a math puzzle. It's almost certainly not the right way to
generate a helix. I thought others might find it interesting. ]
Everybody knows that you can't generate a helix with linear_extrude.
Linear extrude works with horizontal cross sections, and a proper helix
needs a circle (or whatever shape) that's tilted to perpendicular to the
angle of the helix. You end up with something like so:
Some time back, I realized that you could generate a helix with linear
extrude. The problem is that the horizontal cross-section isn't simple.
It's sort of banana-shaped:
But what is that shape?
I got interested in this question again, and played with the idea that
it's a circle that's been stretched around the circumference of the helix.
I tried translating it into polar coordinates and scaling theta by
1/sin(helix angle), and although I'm not sure that it's absolutely right,
the result is pretty good:
Here's a cross-section perpendicular to the helix angle:
Perfect circle? Maybe, maybe not. I'm not sure that I cut the
cross-section at exactly the right point, or took the screen shot from the
right angle.
Here's the demo program, intended for use with the customizer. The best
algorithm, A, is in bananaA(). bananaB() is a different way to stretch the
circle that doesn't really work, but I don't understand why not because I
can't think well in polar coordinates. circle() is a straightforward
circle, like you would get from the "doesn't work" linear extrude
solution. (And yes, of course if I was really trying to write a helix
function everything would be an argument, not a global.)
// Vertical distance from the centerline of one turn to the centerline of the next turn
pitch = 20;
// Radius of the helix, from XY=0 to the centerline of the extruded circle
helix_r = 15;
// Radius of the extruded circle
r = 5;
// Height of the helix
h = 100;
// Show cross-section (view from -Y orthogonal)
intersect = false;
// Which algorithm to use (a is best, b is interesting but not as good, 2 is simple circle)
algorithm = 0; // [ 0: a, 1: b, 2: circle ]
module stop();
// This is a little interesting to animate:
// pitch = 20 + 10abs($t2-1);
function torect2(p) = [
p[0] * cos(p[1]),
p[0] * sin(p[1])
];
function topolar2(p) = [
norm(p),
atan2(p.y, p.x)
];
// Helix angle
helix_a = atan2(pitch, helix_r2PI);
// degrees per unit, along the circumference
theta_scale = 360/(2PIhelix_r);
// Banana, algorithm A
bananaA = function() [
for (a=[0:359])
torect2([helix_r, 0] + [r*cos(a), r * sin(a) * theta_scale / sin(helix_a)])
];
// Banana, algorithm B
bananaB = function() [
for (a=[0:359])
let(circ = torect2([r, a])) // circle
let(tcirc = circ + [helix_r, 0]) // translated
let(pcirc = topolar2(tcirc)) // in polar coords
let(smeared_circ = [pcirc[0], pcirc[1]/sin(helix_a)])
torect2(smeared_circ)
];
// Simple circle, for comparison
circle = function() [
for (a=[0:359])
torect2([r, a]) + [helix_r, 0]
];
functions = [ bananaA, bananaB, circle ];
module helix() {
linear_extrude(height=h, twist=360*h/pitch, convexity=2)
polygon(functionsalgorithm);
}
if (intersect) {
intersection() {
#helix();
translate([helix_r, 0, pitch]) rotate([-helix_a,0,0]) cube([r2, 0.01, r2], center=true);
}
} else {
helix();
}
// A few reference shapes
// A circle. If helix_a is 90, this should match the bottom of the helix.
color("blue") translate([helix_r,0,-0.1]) linear_extrude(height=0.1) circle(r=r);
// The circumference of the helix.
color("green") translate([0,0,-0.2]) linear_extrude(height=0.1) difference() { circle(r=helix_r+0.1); circle(r=helix_r-0.1); }
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On 2/28/2024 3:04 AM, Sanjeev Prabhakar wrote:
Probably you need to write a path extrude function.
I feel this should be part of regular openscad.
It wouldn't be too difficult to write this function, if you can write
such complex models.
I did say that linear extrude was not the right way to generate a helix :-)
Indeed, a path-extrude / sweep module is probably the right way.
I've never tried to write one because I haven't needed one, and because
several libraries already have one.
I've never really talked to anybody about why we don't have one in base
OpenSCAD, but I think one of the key reasons is that nobody has figured
out how to efficiently detect self-intersecting variations. Also it
would be easy to go wild with allowing arbitrary flexibility: start
with the possible desire to control rotation as you move along the path,
and continue with the desire for arbitrary transformations.
I feel it will be a good function or module to have in openscad.
There would be few cases where it may not work 100% as desired but in most
of the cases it will work if written efficiently.
I am sure this will help a lot of people, especially starters who struggle
with hull to create simple shapes like helix.
Why not adopt functions from available libraries if the library authors
are OK with that.
On Wed, 28 Feb, 2024, 9:40 pm Jordan Brown, openscad@jordan.maileater.net
wrote:
On 2/28/2024 3:04 AM, Sanjeev Prabhakar wrote:
Probably you need to write a path extrude function.
I feel this should be part of regular openscad.
It wouldn't be too difficult to write this function, if you can write such
complex models.
I did say that linear extrude was not the right way to generate a helix :-)
Indeed, a path-extrude / sweep module is probably the right way.
I've never tried to write one because I haven't needed one, and because
several libraries already have one.
I've never really talked to anybody about why we don't have one in base
OpenSCAD, but I think one of the key reasons is that nobody has figured out
how to efficiently detect self-intersecting variations. Also it would be
easy to go wild with allowing arbitrary flexibility: start with the
possible desire to control rotation as you move along the path, and
continue with the desire for arbitrary transformations.