AM
Adrian Mariano
Wed, Aug 10, 2022 12:28 AM
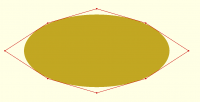
I started wondering about the case of a four-point polygon fit and
whether the problem might just be underdetermined. So I tried running
the process starting with [0,b+extra] and found that I can indeed get
different solutions for a range of values of extra.
I attached two different polygons for the same ellipse with different
extra values. So of course then the question is whether there's an
easy way to find the solution with minimal area. :)
On Mon, Aug 8, 2022 at 6:18 PM Adrian Mariano avm4@cornell.edu wrote:
Did you see my post earlier that actually implements the entire
end-to-end process, including estimating L
When starting at a point there are TWO parameters, L and "extra", the
distance of the point away from the ellipse. If you have extra wrong
you will presumably never get a solution no matter how much you fiddle
with L. This could be addressed by hitting with a 2d optimization
method, but as I said, that seems overcomplex and I don't have such a
code implemented in OpenSCAD.
Actually I was just thinking a bit more about the case of starting a
quadrant and ending on a flat. That means start at [b,L/2] and end on
[a,L/2]. I tweaked the code to end with y=L/2 and it fails. That is,
the resulting point it finds doesn't have x=b. But there doesn't seem
to be another degree of freedom. It would therefore appear that the
case of four flat ellipse ends is generally impossible. Have I missed
something?
On Mon, Aug 8, 2022 at 5:37 PM Father Horton fatherhorton@gmail.com wrote:
You change L until it works. I'd start with an estimate (Ramanujan's?) of the perimeter of the ellipse and divide by N to get an estimate for L. Step around and if L is too short, increase it by say 10%, and if it's too long, decrease by 10%. Once you have the right distance bracketed, do a binary search.
On Mon, Aug 8, 2022 at 4:29 PM Adrian Mariano avm4@cornell.edu wrote:
So that code just works around the ellipse, making 3 steps at the
fixed length, right? The hard part isn't doing that---it's being able
to automatically update so that you get the correct answer. What
happens if you try to do this manual process but for an ellipse that
starts with a full segment whose endpoint is [0,b+extra] for some
extra corner offset distance? Or one that starts the same but ends at
[b,L/2]. I haven't actually tried running these processes to see how
it behaves.
On Mon, Aug 8, 2022 at 4:47 PM Father Horton fatherhorton@gmail.com wrote:
Here's a Python version that gets the first quadrant right:
import math
major = 2
minor = 1
length = 1.03
px = length / 2
py = minor
for i in range(1, 3):
c = px / major
d = py / minor
print(f"Adjusted point off circle is ({c:.3f},{d:.3f})")
a = (2 * c + math.sqrt(4 * c * c - 4 * (d * d + c * c) * (1 - d * d))) / (2 * (d * d + c * c))
b = math.sqrt(1 - a * a)
print(f"Point on circle is ({a:.3f}, {b:.3f})")
ex = a * major
ey = b * minor
print(f"Point on ellipse is ({ex:.3f}, {ey:.3f})")
m = (py - ey) / (px - ex)
xhat = math.sqrt(length * length / (1 + m * m))
yhat = m * xhat
px = px + xhat
py = py + yhat
print(f"New point off circle is ({px:.3f}, {py:.3f})")
On Mon, Aug 8, 2022 at 3:41 PM Adrian Mariano avm4@cornell.edu wrote:
It's never necessary to do more than half the ellipse, which I think
makes handling the multiplicity of tangents easier.
On Mon, Aug 8, 2022 at 4:30 PM Father Horton fatherhorton@gmail.com wrote:
y and x if divisible by 4, right?
Right, which would make calculation easier since I wouldn't have to deal with those nasty quadrant changes.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I started wondering about the case of a four-point polygon fit and
whether the problem might just be underdetermined. So I tried running
the process starting with [0,b+extra] and found that I can indeed get
different solutions for a range of values of extra.
I attached two different polygons for the same ellipse with different
extra values. So of course then the question is whether there's an
easy way to find the solution with minimal area. :)
On Mon, Aug 8, 2022 at 6:18 PM Adrian Mariano <avm4@cornell.edu> wrote:
>
> Did you see my post earlier that actually implements the entire
> end-to-end process, including estimating L
>
> When starting at a point there are TWO parameters, L and "extra", the
> distance of the point away from the ellipse. If you have extra wrong
> you will presumably never get a solution no matter how much you fiddle
> with L. This could be addressed by hitting with a 2d optimization
> method, but as I said, that seems overcomplex and I don't have such a
> code implemented in OpenSCAD.
>
> Actually I was just thinking a bit more about the case of starting a
> quadrant and ending on a flat. That means start at [b,L/2] and end on
> [a,L/2]. I tweaked the code to end with y=L/2 and it fails. That is,
> the resulting point it finds doesn't have x=b. But there doesn't seem
> to be another degree of freedom. It would therefore appear that the
> case of four flat ellipse ends is generally impossible. Have I missed
> something?
>
> On Mon, Aug 8, 2022 at 5:37 PM Father Horton <fatherhorton@gmail.com> wrote:
> >
> > You change L until it works. I'd start with an estimate (Ramanujan's?) of the perimeter of the ellipse and divide by N to get an estimate for L. Step around and if L is too short, increase it by say 10%, and if it's too long, decrease by 10%. Once you have the right distance bracketed, do a binary search.
> >
> > On Mon, Aug 8, 2022 at 4:29 PM Adrian Mariano <avm4@cornell.edu> wrote:
> >>
> >> So that code just works around the ellipse, making 3 steps at the
> >> fixed length, right? The hard part isn't doing that---it's being able
> >> to automatically update so that you get the correct answer. What
> >> happens if you try to do this manual process but for an ellipse that
> >> starts with a full segment whose endpoint is [0,b+extra] for some
> >> extra corner offset distance? Or one that starts the same but ends at
> >> [b,L/2]. I haven't actually tried running these processes to see how
> >> it behaves.
> >>
> >> On Mon, Aug 8, 2022 at 4:47 PM Father Horton <fatherhorton@gmail.com> wrote:
> >> >
> >> > Here's a Python version that gets the first quadrant right:
> >> >
> >> > import math
> >> >
> >> > major = 2
> >> > minor = 1
> >> >
> >> > length = 1.03
> >> >
> >> > px = length / 2
> >> > py = minor
> >> >
> >> > for i in range(1, 3):
> >> > c = px / major
> >> > d = py / minor
> >> > print(f"Adjusted point off circle is ({c:.3f},{d:.3f})")
> >> >
> >> >
> >> > a = (2 * c + math.sqrt(4 * c * c - 4 * (d * d + c * c) * (1 - d * d))) / (2 * (d * d + c * c))
> >> > b = math.sqrt(1 - a * a)
> >> >
> >> > print(f"Point on circle is ({a:.3f}, {b:.3f})")
> >> >
> >> > ex = a * major
> >> > ey = b * minor
> >> > print(f"Point on ellipse is ({ex:.3f}, {ey:.3f})")
> >> >
> >> > m = (py - ey) / (px - ex)
> >> > xhat = math.sqrt(length * length / (1 + m * m))
> >> > yhat = m * xhat
> >> > px = px + xhat
> >> > py = py + yhat
> >> >
> >> > print(f"New point off circle is ({px:.3f}, {py:.3f})")
> >> >
> >> >
> >> > On Mon, Aug 8, 2022 at 3:41 PM Adrian Mariano <avm4@cornell.edu> wrote:
> >> >>
> >> >> It's never necessary to do more than half the ellipse, which I think
> >> >> makes handling the multiplicity of tangents easier.
> >> >>
> >> >> On Mon, Aug 8, 2022 at 4:30 PM Father Horton <fatherhorton@gmail.com> wrote:
> >> >> >
> >> >> >
> >> >> >
> >> >> > On Mon, Aug 8, 2022 at 3:23 PM Michael Möller <private2michael@gmail.com> wrote:
> >> >> >>
> >> >> >> y and x if divisible by 4, right?
> >> >> >
> >> >> >
> >> >> > Right, which would make calculation easier since I wouldn't have to deal with those nasty quadrant changes.
> >> >> > _______________________________________________
> >> >> > OpenSCAD mailing list
> >> >> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> >> >> _______________________________________________
> >> >> OpenSCAD mailing list
> >> >> To unsubscribe send an email to discuss-leave@lists.openscad.org
> >> >
> >> > _______________________________________________
> >> > OpenSCAD mailing list
> >> > To unsubscribe send an email to discuss-leave@lists.openscad.org
> >> _______________________________________________
> >> OpenSCAD mailing list
> >> To unsubscribe send an email to discuss-leave@lists.openscad.org
> >
> > _______________________________________________
> > OpenSCAD mailing list
> > To unsubscribe send an email to discuss-leave@lists.openscad.org