Generating a helix with linear extrude
[ This was a math puzzle. It's almost certainly not the right way to
generate a helix. I thought others might find it interesting. ]
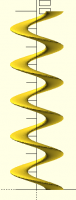
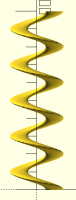
Everybody knows that you can't generate a helix with linear_extrude.
Linear extrude works with horizontal cross sections, and a proper helix
needs a circle (or whatever shape) that's tilted to perpendicular to the
angle of the helix. You end up with something like so:
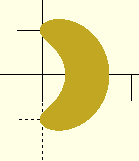
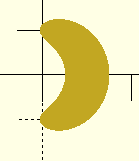
Some time back, I realized that you could generate a helix with linear
extrude. The problem is that the horizontal cross-section isn't
simple. It's sort of banana-shaped:
But what is that shape?
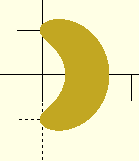
I got interested in this question again, and played with the idea that
it's a circle that's been stretched around the circumference of the helix.
I tried translating it into polar coordinates and scaling theta by
1/sin(helix angle), and although I'm not sure that it's absolutely
right, the result is pretty good:
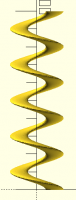
Here's a cross-section perpendicular to the helix angle:
Perfect circle? Maybe, maybe not. I'm not sure that I cut the
cross-section at exactly the right point, or took the screen shot from
the right angle.
Here's the demo program, intended for use with the customizer. The best
algorithm, A, is in bananaA(). bananaB() is a different way to stretch
the circle that doesn't really work, but I don't understand why not
because I can't think well in polar coordinates. circle() is a
straightforward circle, like you would get from the "doesn't work"
linear extrude solution. (And yes, of course if I was really trying to
write a helix function everything would be an argument, not a global.)
// Vertical distance from the centerline of one turn to the centerline of the next turn
pitch = 20;
// Radius of the helix, from XY=0 to the centerline of the extruded circle
helix_r = 15;
// Radius of the extruded circle
r = 5;
// Height of the helix
h = 100;
// Show cross-section (view from -Y orthogonal)
intersect = false;
// Which algorithm to use (a is best, b is interesting but not as good, 2 is simple circle)
algorithm = 0; // [ 0: a, 1: b, 2: circle ]
module stop();
// This is a little interesting to animate:
// pitch = 20 + 10abs($t2-1);
function torect2(p) = [
p[0] * cos(p[1]),
p[0] * sin(p[1])
];
function topolar2(p) = [
norm(p),
atan2(p.y, p.x)
];
// Helix angle
helix_a = atan2(pitch, helix_r2PI);
// degrees per unit, along the circumference
theta_scale = 360/(2PIhelix_r);
// Banana, algorithm A
bananaA = function() [
for (a=[0:359])
torect2([helix_r, 0] + [r*cos(a), r * sin(a) * theta_scale / sin(helix_a)])
];
// Banana, algorithm B
bananaB = function() [
for (a=[0:359])
let(circ = torect2([r, a])) // circle
let(tcirc = circ + [helix_r, 0]) // translated
let(pcirc = topolar2(tcirc)) // in polar coords
let(smeared_circ = [pcirc[0], pcirc[1]/sin(helix_a)])
torect2(smeared_circ)
];
// Simple circle, for comparison
circle = function() [
for (a=[0:359])
torect2([r, a]) + [helix_r, 0]
];
functions = [ bananaA, bananaB, circle ];
module helix() {
linear_extrude(height=h, twist=360*h/pitch, convexity=2)
polygon(functionsalgorithm);
}
if (intersect) {
intersection() {
#helix();
translate([helix_r, 0, pitch]) rotate([-helix_a,0,0]) cube([r2, 0.01, r2], center=true);
}
} else {
helix();
}
// A few reference shapes
// A circle. If helix_a is 90, this should match the bottom of the helix.
color("blue") translate([helix_r,0,-0.1]) linear_extrude(height=0.1) circle(r=r);
// The circumference of the helix.
color("green") translate([0,0,-0.2]) linear_extrude(height=0.1) difference() { circle(r=helix_r+0.1); circle(r=helix_r-0.1); }
Here is my solution from ~8.5 yrs ago
https://www.thingiverse.com/thing:1098806
On Mon, Feb 26, 2024 at 11:59 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
[ This was a math puzzle. It's almost certainly not the right way to
generate a helix. I thought others might find it interesting. ]
Everybody knows that you can't generate a helix with linear_extrude.
Linear extrude works with horizontal cross sections, and a proper helix
needs a circle (or whatever shape) that's tilted to perpendicular to the
angle of the helix. You end up with something like so:
Some time back, I realized that you could generate a helix with linear
extrude. The problem is that the horizontal cross-section isn't simple.
It's sort of banana-shaped:
But what is that shape?
I got interested in this question again, and played with the idea that
it's a circle that's been stretched around the circumference of the helix.
I tried translating it into polar coordinates and scaling theta by
1/sin(helix angle), and although I'm not sure that it's absolutely right,
the result is pretty good:
Here's a cross-section perpendicular to the helix angle:
Perfect circle? Maybe, maybe not. I'm not sure that I cut the
cross-section at exactly the right point, or took the screen shot from the
right angle.
Here's the demo program, intended for use with the customizer. The best
algorithm, A, is in bananaA(). bananaB() is a different way to stretch the
circle that doesn't really work, but I don't understand why not because I
can't think well in polar coordinates. circle() is a straightforward
circle, like you would get from the "doesn't work" linear extrude
solution. (And yes, of course if I was really trying to write a helix
function everything would be an argument, not a global.)
// Vertical distance from the centerline of one turn to the centerline of the next turn
pitch = 20;
// Radius of the helix, from XY=0 to the centerline of the extruded circle
helix_r = 15;
// Radius of the extruded circle
r = 5;
// Height of the helix
h = 100;
// Show cross-section (view from -Y orthogonal)
intersect = false;
// Which algorithm to use (a is best, b is interesting but not as good, 2 is simple circle)
algorithm = 0; // [ 0: a, 1: b, 2: circle ]
module stop();
// This is a little interesting to animate:
// pitch = 20 + 10abs($t2-1);
function torect2(p) = [
p[0] * cos(p[1]),
p[0] * sin(p[1])
];
function topolar2(p) = [
norm(p),
atan2(p.y, p.x)
];
// Helix angle
helix_a = atan2(pitch, helix_r2PI);
// degrees per unit, along the circumference
theta_scale = 360/(2PIhelix_r);
// Banana, algorithm A
bananaA = function() [
for (a=[0:359])
torect2([helix_r, 0] + [r*cos(a), r * sin(a) * theta_scale / sin(helix_a)])
];
// Banana, algorithm B
bananaB = function() [
for (a=[0:359])
let(circ = torect2([r, a])) // circle
let(tcirc = circ + [helix_r, 0]) // translated
let(pcirc = topolar2(tcirc)) // in polar coords
let(smeared_circ = [pcirc[0], pcirc[1]/sin(helix_a)])
torect2(smeared_circ)
];
// Simple circle, for comparison
circle = function() [
for (a=[0:359])
torect2([r, a]) + [helix_r, 0]
];
functions = [ bananaA, bananaB, circle ];
module helix() {
linear_extrude(height=h, twist=360*h/pitch, convexity=2)
polygon(functionsalgorithm);
}
if (intersect) {
intersection() {
#helix();
translate([helix_r, 0, pitch]) rotate([-helix_a,0,0]) cube([r2, 0.01, r2], center=true);
}
} else {
helix();
}
// A few reference shapes
// A circle. If helix_a is 90, this should match the bottom of the helix.
color("blue") translate([helix_r,0,-0.1]) linear_extrude(height=0.1) circle(r=r);
// The circumference of the helix.
color("green") translate([0,0,-0.2]) linear_extrude(height=0.1) difference() { circle(r=helix_r+0.1); circle(r=helix_r-0.1); }
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I am absolutely stunned that it's possible to create a flat cross-section
such that the final result looks correctly, when extruded!
However, I feel a helix would look more natural when the top/bottom face of
the helix would be normal to the natural extrusion.
Being able to tilt the extruded 2d shape has its justification :)
On Tue, Feb 27, 2024 at 11:50 PM Hans L via Discuss <
discuss@lists.openscad.org> wrote:
Here is my solution from ~8.5 yrs ago
https://www.thingiverse.com/thing:1098806
On Mon, Feb 26, 2024 at 11:59 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
[ This was a math puzzle. It's almost certainly not the right way to
generate a helix. I thought others might find it interesting. ]
Everybody knows that you can't generate a helix with linear_extrude.
Linear extrude works with horizontal cross sections, and a proper helix
needs a circle (or whatever shape) that's tilted to perpendicular to the
angle of the helix. You end up with something like so:
Some time back, I realized that you could generate a helix with linear
extrude. The problem is that the horizontal cross-section isn't simple.
It's sort of banana-shaped:
But what is that shape?
I got interested in this question again, and played with the idea that
it's a circle that's been stretched around the circumference of the helix.
I tried translating it into polar coordinates and scaling theta by
1/sin(helix angle), and although I'm not sure that it's absolutely right,
the result is pretty good:
Here's a cross-section perpendicular to the helix angle:
Perfect circle? Maybe, maybe not. I'm not sure that I cut the
cross-section at exactly the right point, or took the screen shot from the
right angle.
Here's the demo program, intended for use with the customizer. The best
algorithm, A, is in bananaA(). bananaB() is a different way to stretch the
circle that doesn't really work, but I don't understand why not because I
can't think well in polar coordinates. circle() is a straightforward
circle, like you would get from the "doesn't work" linear extrude
solution. (And yes, of course if I was really trying to write a helix
function everything would be an argument, not a global.)
// Vertical distance from the centerline of one turn to the centerline of the next turn
pitch = 20;
// Radius of the helix, from XY=0 to the centerline of the extruded circle
helix_r = 15;
// Radius of the extruded circle
r = 5;
// Height of the helix
h = 100;
// Show cross-section (view from -Y orthogonal)
intersect = false;
// Which algorithm to use (a is best, b is interesting but not as good, 2 is simple circle)
algorithm = 0; // [ 0: a, 1: b, 2: circle ]
module stop();
// This is a little interesting to animate:
// pitch = 20 + 10abs($t2-1);
function torect2(p) = [
p[0] * cos(p[1]),
p[0] * sin(p[1])
];
function topolar2(p) = [
norm(p),
atan2(p.y, p.x)
];
// Helix angle
helix_a = atan2(pitch, helix_r2PI);
// degrees per unit, along the circumference
theta_scale = 360/(2PIhelix_r);
// Banana, algorithm A
bananaA = function() [
for (a=[0:359])
torect2([helix_r, 0] + [r*cos(a), r * sin(a) * theta_scale / sin(helix_a)])
];
// Banana, algorithm B
bananaB = function() [
for (a=[0:359])
let(circ = torect2([r, a])) // circle
let(tcirc = circ + [helix_r, 0]) // translated
let(pcirc = topolar2(tcirc)) // in polar coords
let(smeared_circ = [pcirc[0], pcirc[1]/sin(helix_a)])
torect2(smeared_circ)
];
// Simple circle, for comparison
circle = function() [
for (a=[0:359])
torect2([r, a]) + [helix_r, 0]
];
functions = [ bananaA, bananaB, circle ];
module helix() {
linear_extrude(height=h, twist=360*h/pitch, convexity=2)
polygon(functionsalgorithm);
}
if (intersect) {
intersection() {
#helix();
translate([helix_r, 0, pitch]) rotate([-helix_a,0,0]) cube([r2, 0.01, r2], center=true);
}
} else {
helix();
}
// A few reference shapes
// A circle. If helix_a is 90, this should match the bottom of the helix.
color("blue") translate([helix_r,0,-0.1]) linear_extrude(height=0.1) circle(r=r);
// The circumference of the helix.
color("green") translate([0,0,-0.2]) linear_extrude(height=0.1) difference() { circle(r=helix_r+0.1); circle(r=helix_r-0.1); }
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org