Re: parametric
I don't have an algorithm at all. I was looking for one, though :-)
Look at the sample pictures I sent as just being stl objects. What would I
need to do to create them in OpenSCAD? How do you create odd shaped
"blobs" and patterns and put them together?
Joe Weinpert
skidrowacademy.com
On Mon, Oct 28, 2024 at 5:20 PM Adrian Mariano avm4@cornell.edu wrote:
Appears that you sent this message just to me, not the list.
Do you have an algorithm that generates these parametric structures?
Because there are two separate issues here. One is how do you produce
those patterns AT ALL. And the second one is how do you do it in
OpenSCAD. It would be advantageous to have a solid answer to the first
question before pondering the second one. Or you at least need some idea
of a possible algorithm. An algorithm for this is not immediately obvious
to me. The problem of "how to do this in BOSL2" depends on what that
algorithm looks like, and a lot of it might not be BOSL2 specific but
really just how to generate a pattern that looks like that.
On Sat, Oct 26, 2024 at 12:53 PM Joe Weinpert joe.weinpert@gmail.com
wrote:
Here are a couple of samples. Parametric styles vary immensely. It
would be nice to have a tool that can be used to create different forms.
[image: 2024-10-26_12-46-24.jpg]
[image: 2024-10-26_12-48-31.jpg]
Joe Weinpert
skidrowacademy.com
On Sat, Oct 26, 2024 at 12:40 PM Adrian Mariano avm4@cornell.edu wrote:
You need to define your goal better. I have no clue what a parametric
wall carving might be. What form? What parameters?
On Sat, Oct 26, 2024 at 12:23 Joe Weinpert via Discuss <
discuss@lists.openscad.org> wrote:
I would like to use OpenSCAD and the BOSL library to design parametric
wood wall carving STL files.
Has anyone done this yet?
Where should I start looking? BOSL has nearly 900 functions.
Would there be any examples of what to use? Examples, I have found,
are the best way to learn something.
Joe Weinpert
skidrowacademy.com
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
On 10/28/2024 2:34 PM, Joe Weinpert via Discuss wrote:
I don't have an algorithm at all. I was looking for one, though :-)
Look at the sample pictures I sent as just being stl objects. What
would I need to do to create them in OpenSCAD? How do you create odd
shaped "blobs" and patterns and put them together?
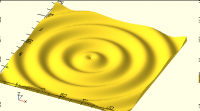
polyhedron(), and math to come up with the desired shape.
Here's something I did to come up with a water wave pattern. It's not
great but it illustrates the idea. The bulk is the sfc() module, which
is like surface() but takes its input in the form of an array.
surface() really should do that, but doesn't and I haven't gotten around
to making it happen. I was never very happy with the relationship
between the resolution of the array and the size presented, so that may
be more complex than it needs to be.
For something like you describe, you need the sfc() module and a module
that produces the right height-map for your pattern.
$fa = 1;
$fs = 0.5;
waterX = 600;
waterY = 600;
waterStep = 5;
waveLengthX = 60;
waveLengthY = 50;
waveAmpX = 2;
waveAmpY = 1;
waveH = waveAmpX + waveAmpY;
baseH = waveH + 0.5;
function wave(x,y) = waveAmpXsin(360x/waveLengthX) + waveAmpYsin(360y/waveLengthY);
module water() {
water = [
let(nx = floor(waterX/waterStep))
let(xStep = waterX/nx)
let(ny = floor(waterY/waterStep))
let(yStep = waterY/ny)
for (ix = [0:nx]) [
for (iy=[0:ny])
wave(ixxStep, iyyStep)
]
];
translate([-waterX/4,-waterY/4,waveH])
sfc(water, [waterX, waterY, baseH]);
}
module sfc(a, sz) {
function dataIndex(x, y) = dataBase + x*ny + y;
nx = len(a);
ny = len(a[0]);
corners = 0;
dataBase = corners + 4;
pts = [
[0, 0, -sz.z],
[nx-1, 0, -sz.z],
[nx-1, ny-1, -sz.z],
[0, ny-1, -sz.z],
for (x = [0:nx-1])
for (y = [0:ny-1])
[ x, y, a[x][y] ]
];
faces = [
[ corners+0, corners+1, corners+2 ],
[ corners+0, corners+2, corners+3 ],
[
each for (x=[0:nx-1]) dataIndex(x,0),
corners+1,
corners+0,
],
[
each for (y=[0:ny-1]) dataIndex(nx-1,y),
corners+2,
corners+1,
],
[
each for (x=[nx-1:-1:0]) dataIndex(x,ny-1),
corners+3,
corners+2,
],
[
each for (y=[ny-1:-1:0]) dataIndex(0,y),
corners+0,
corners+3,
],
each for (x=[0:nx-2], y=[0:ny-2]) [
[ dataIndex(x+1, y), dataIndex(x, y), dataIndex(x, y+1) ],
[ dataIndex(x+1, y+1), dataIndex(x+1, y), dataIndex(x, y+1) ],
],
];
scale([sz.x/(nx-1),sz.y/(ny-1),1])
polyhedron(pts, faces, convexity=ceil(max(waterX/waveLengthX, waterY/waveLengthY)));
}
water();
And of course that prompted me to review that program, simplify it a
bit, and replace the wave function with one that's in some ways more
interesting.
But note that the shape of the model is entirely controlled by the
wave() function and its inputs.
Note: sfc() has a bunch of square cells to draw a surface from. That
requires deciding which diagonal to use to split the squares into two
triangles. It happens that it chooses the lower-right/upper-left
diagonal, but either is equally correct. In other patterns I've found
that this uniform triangulation can produce undesirable visual
artifacts, so in some other variations on this module I've chosen which
to use at random. The difference is in how the final "each for" is built.
And of course, BOSL2 has this in its heightfield() module:
https://github.com/BelfrySCAD/BOSL2/wiki/shapes3d.scad#functionmodule-heightfield
waterSize = [120, 120];
waveLength = 20;
waveH = 2;
baseH = waveH + 0.5;
water(waterSize);
function wave(x, y) = sin(360*norm([x,y] - waterSize/2)/waveLength) * waveH;
module water(size) {
water = [
for (ix = [0:size.x]) [
for (iy=[0:size.y])
wave(ix, iy)
]
];
sfc(water, baseH);
}
module sfc(a, base, convexity=10) {
function dataIndex(x, y) = dataBase + x*ny + y;
nx = len(a);
ny = len(a[0]);
corners = 0;
dataBase = corners + 4;
pts = [
[0, 0, -base],
[nx-1, 0, -base],
[nx-1, ny-1, -base],
[0, ny-1, -base],
for (x = [0:nx-1])
for (y = [0:ny-1])
[ x, y, a[x][y] ]
];
faces = [
[ corners+0, corners+1, corners+2 ],
[ corners+0, corners+2, corners+3 ],
[
each for (x=[0:nx-1]) dataIndex(x,0),
corners+1,
corners+0,
],
[
each for (y=[0:ny-1]) dataIndex(nx-1,y),
corners+2,
corners+1,
],
[
each for (x=[nx-1:-1:0]) dataIndex(x,ny-1),
corners+3,
corners+2,
],
[
each for (y=[ny-1:-1:0]) dataIndex(0,y),
corners+0,
corners+3,
],
each for (x=[0:nx-2], y=[0:ny-2]) [
[ dataIndex(x+1, y), dataIndex(x, y), dataIndex(x, y+1) ],
[ dataIndex(x+1, y+1), dataIndex(x+1, y), dataIndex(x, y+1) ],
],
];
polyhedron(pts, faces, convexity=convexity);
}
@Joe, that is SO CooL! Thanks for the examples. Hmmm... I'll have to make
some time to work on a dream project -- it really came to me in a dream,
and it is one of about 6 blacksmithing projects that I hope to make before
I put my hammers to rest. But to REALLY give it a go, I need to find
someone to help me translate the poem that came to me in the dream into
Japanese, and then work with my best friend to render that with dry-brush
calligraphy, then execute the calligraphy in steel (which plunges into the
background stone, which ripples like waves in water)... Aaahhhh <sigh> I
still dream ;-)
On Mon, Oct 28, 2024 at 6:27 PM Jordan Brown via Discuss <
discuss@lists.openscad.org> wrote:
And of course that prompted me to review that program, simplify it a bit,
and replace the wave function with one that's in some ways more interesting.
But note that the shape of the model is entirely controlled by the wave()
function and its inputs.
Note: sfc() has a bunch of square cells to draw a surface from. That
requires deciding which diagonal to use to split the squares into two
triangles. It happens that it chooses the lower-right/upper-left diagonal,
but either is equally correct. In other patterns I've found that this
uniform triangulation can produce undesirable visual artifacts, so in some
other variations on this module I've chosen which to use at random. The
difference is in how the final "each for" is built.
And of course, BOSL2 has this in its heightfield() module:
https://github.com/BelfrySCAD/BOSL2/wiki/shapes3d.scad#functionmodule-heightfield
waterSize = [120, 120];
waveLength = 20;
waveH = 2;
baseH = waveH + 0.5;
water(waterSize);
function wave(x, y) = sin(360*norm([x,y] - waterSize/2)/waveLength) * waveH;
module water(size) {
water = [
for (ix = [0:size.x]) [
for (iy=[0:size.y])
wave(ix, iy)
]
];
sfc(water, baseH);
}
module sfc(a, base, convexity=10) {
function dataIndex(x, y) = dataBase + x*ny + y;
nx = len(a);
ny = len(a[0]);
corners = 0;
dataBase = corners + 4;
pts = [
[0, 0, -base],
[nx-1, 0, -base],
[nx-1, ny-1, -base],
[0, ny-1, -base],
for (x = [0:nx-1])
for (y = [0:ny-1])
[ x, y, a[x][y] ]
];
faces = [
[ corners+0, corners+1, corners+2 ],
[ corners+0, corners+2, corners+3 ],
[
each for (x=[0:nx-1]) dataIndex(x,0),
corners+1,
corners+0,
],
[
each for (y=[0:ny-1]) dataIndex(nx-1,y),
corners+2,
corners+1,
],
[
each for (x=[nx-1:-1:0]) dataIndex(x,ny-1),
corners+3,
corners+2,
],
[
each for (y=[ny-1:-1:0]) dataIndex(0,y),
corners+0,
corners+3,
],
each for (x=[0:nx-2], y=[0:ny-2]) [
[ dataIndex(x+1, y), dataIndex(x, y), dataIndex(x, y+1) ],
[ dataIndex(x+1, y+1), dataIndex(x+1, y), dataIndex(x, y+1) ],
],
];
polyhedron(pts, faces, convexity=convexity);
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Meant to include an image...
I don't think the waves problem gives much insight into the general
parametric problem that was posed. Producing that general parametric
pattern as a function over the xy plane seems like it might be difficult.
I suppose there might be some cool generative method that used an iterative
process to produce a functional shape like that.
When I looked at it I thought maybe you could generate a set of paths for
each ridge (or cut, if you like). I thought maybe this could be turned
into a texture, but that's hard. So that leads to something like this
(where you might be able to get away regular path_sweep if there are more
gentle curves---it would be faster). But I have no clue how you generate
the path list.
include<BOSL2/std.scad>
cuboid([10,10,1],anchor=TOP+LEFT);
cycles=3;
path = [for(t=[0:10:360cycles]) [10t/360/cycles,
(1+t/(360*cycles)/.5)*sin(t)]];
profile = [for(theta=[-180:36:180]) [theta/180/3, (1+cos(theta))/7]];
path_sweep2d(profile, path);
[image: image.png]
On Mon, Oct 28, 2024 at 5:56 PM Jordan Brown openscad@jordan.maileater.net
wrote:
On 10/28/2024 2:34 PM, Joe Weinpert via Discuss wrote:
I don't have an algorithm at all. I was looking for one, though :-)
Look at the sample pictures I sent as just being stl objects. What would
I need to do to create them in OpenSCAD? How do you create odd shaped
"blobs" and patterns and put them together?
polyhedron(), and math to come up with the desired shape.
Here's something I did to come up with a water wave pattern. It's not
great but it illustrates the idea. The bulk is the sfc() module, which is
like surface() but takes its input in the form of an array. surface()
really should do that, but doesn't and I haven't gotten around to making it
happen. I was never very happy with the relationship between the
resolution of the array and the size presented, so that may be more complex
than it needs to be.
For something like you describe, you need the sfc() module and a module
that produces the right height-map for your pattern.
$fa = 1;
$fs = 0.5;
waterX = 600;
waterY = 600;
waterStep = 5;
waveLengthX = 60;
waveLengthY = 50;
waveAmpX = 2;
waveAmpY = 1;
waveH = waveAmpX + waveAmpY;
baseH = waveH + 0.5;
function wave(x,y) = waveAmpXsin(360x/waveLengthX) + waveAmpYsin(360y/waveLengthY);
module water() {
water = [
let(nx = floor(waterX/waterStep))
let(xStep = waterX/nx)
let(ny = floor(waterY/waterStep))
let(yStep = waterY/ny)
for (ix = [0:nx]) [
for (iy=[0:ny])
wave(ixxStep, iyyStep)
]
];
translate([-waterX/4,-waterY/4,waveH])
sfc(water, [waterX, waterY, baseH]);
}
module sfc(a, sz) {
function dataIndex(x, y) = dataBase + x*ny + y;
nx = len(a);
ny = len(a[0]);
corners = 0;
dataBase = corners + 4;
pts = [
[0, 0, -sz.z],
[nx-1, 0, -sz.z],
[nx-1, ny-1, -sz.z],
[0, ny-1, -sz.z],
for (x = [0:nx-1])
for (y = [0:ny-1])
[ x, y, a[x][y] ]
];
faces = [
[ corners+0, corners+1, corners+2 ],
[ corners+0, corners+2, corners+3 ],
[
each for (x=[0:nx-1]) dataIndex(x,0),
corners+1,
corners+0,
],
[
each for (y=[0:ny-1]) dataIndex(nx-1,y),
corners+2,
corners+1,
],
[
each for (x=[nx-1:-1:0]) dataIndex(x,ny-1),
corners+3,
corners+2,
],
[
each for (y=[ny-1:-1:0]) dataIndex(0,y),
corners+0,
corners+3,
],
each for (x=[0:nx-2], y=[0:ny-2]) [
[ dataIndex(x+1, y), dataIndex(x, y), dataIndex(x, y+1) ],
[ dataIndex(x+1, y+1), dataIndex(x+1, y), dataIndex(x, y+1) ],
],
];
scale([sz.x/(nx-1),sz.y/(ny-1),1])
polyhedron(pts, faces, convexity=ceil(max(waterX/waveLengthX, waterY/waveLengthY)));
}
water();
On 10/28/2024 4:06 PM, Adrian Mariano wrote:
I don't think the waves problem gives much insight into the general
parametric problem that was posed.
There are really two distinct problems:
- Given a function of X and Y that tells you the height, produce a
model. We've got that - either your heightfield() or my sfc(). - What function produces the shape that the OP wants?
I'm not quite as pessimistic as you are. Remember that the "function"
doesn't need to be a mathematical function per se; it can have things
like lookup() in it.
But figuring it out won't be trivial.
Come to think of it, the easiest answer might be to draw the desired
pattern (with shading) in Paint or the equivalent, and then bring it in
with surface().
I absolutely agree that there are two separate problems: (1) define what
you're trying to model and (2) actually model it. But I believe that
you've proposed just one approach: write a function that produces the
desired output, then feed it to heightfield(). But that might not be the
easiest approach.
If by "parametric" he means the thing that term usually means, then he
wants something that has a bunch of knobs you turn and produces different
looking results, so "draw it in other software" doesn't qualify.
It might be the case that producing the above specified function is hard
and that it's easier to produce a list of cut or ridge lines. Then you
can't use height field unless you can turn cut lines into a function, which
is a pain because you have to apply a point spread operation that is
perpendicular to the cutline....which is basically like doing path sweep on
the cut line but for a function. So instead...use path_sweep().
On the other hand, there might be as I suggested, some iterative method
with parameters that produces functional outputs that look like what Joe
wants. And if you can do it as a functional form then you can make a
texture and apply it to cylinders and other shapes as well, which seems
like it would be interesting.
On Tue, Oct 29, 2024 at 12:27 AM Jordan Brown openscad@jordan.maileater.net
wrote:
On 10/28/2024 4:06 PM, Adrian Mariano wrote:
I don't think the waves problem gives much insight into the general
parametric problem that was posed.
There are really two distinct problems:
- Given a function of X and Y that tells you the height, produce a
model. We've got that - either your heightfield() or my sfc().
- What function produces the shape that the OP wants?
I'm not quite as pessimistic as you are. Remember that the "function"
doesn't need to be a mathematical function per se; it can have things like
lookup() in it.
But figuring it out won't be trivial.
Come to think of it, the easiest answer might be to draw the desired
pattern (with shading) in Paint or the equivalent, and then bring it in
with surface().
I didn't quite catch the beginning of this discussion. But maybe
interesting anyway....
Because programming an algorithm in openscad might be difficult it
might be better to just do it in python and then export to openscad
syntax.
GIVEN a set of 3D curves, find a surface that matches the
set-of-curves.
If you just randomly "do stuff" then things become a mess. What do I
mean with "matches". Well, if you give a human a point cloud or a
set-of-curves, we immediately imagine the object they belong to. How
to capture that mathematically? I'd think soap surface comes close:
Minimal area of the surface.
I think I have an algorithm that is possibly perfect, possibly
close-but-not-quite.
Between each pair of curves, for each linesegment on one find the
closest point to the linesegment on the other curve. I'm not sure if
you have to take the sum of the linesegments or the actual distance to
the line. That's a triangle of your surface. For "well behaved"
curves, this gives the optimal surface. If there are not "well
behaved" curves that give a surface with holes... I don't know.
So for Jordan's example you could pass in something like:
a=5;
for (i=[0:.3:50])
translate ([0,0,asin(i360*4/50)]) circle (r=i);
or the radials. In openscad you can create a list-of-points with a
sinewave as the Z coordinate in one go. But I haven't memorized the
syntax yet.
(Initially / forever it is NOT the task of the algorithm to figure out
which pairs of curves to use for the surface. The user will have to
pass them in in sequence).
Being able to define surfaces (2d objects in 3D), would eventually
allow users to stitch them together (like we can already with
triangles) and create 3D objects. My example above together with
cylinder-surface (top=false) would create a real 3D object.
Roger.
On Mon, Oct 28, 2024 at 07:06:25PM -0400, Adrian Mariano via Discuss wrote:
I don't think the waves problem gives much insight into the general
parametric problem that was posed. Producing that general parametric
pattern as a function over the xy plane seems like it might be difficult.
I suppose there might be some cool generative method that used an iterative
process to produce a functional shape like that.
When I looked at it I thought maybe you could generate a set of paths for
each ridge (or cut, if you like). I thought maybe this could be turned
into a texture, but that's hard. So that leads to something like this
(where you might be able to get away regular path_sweep if there are more
gentle curves---it would be faster). But I have no clue how you generate
the path list.
include<BOSL2/std.scad>
cuboid([10,10,1],anchor=TOP+LEFT);
cycles=3;
path = [for(t=[0:10:360cycles]) [10t/360/cycles,
(1+t/(360*cycles)/.5)*sin(t)]];
profile = [for(theta=[-180:36:180]) [theta/180/3, (1+cos(theta))/7]];
path_sweep2d(profile, path);
[image: image.png]
On Mon, Oct 28, 2024 at 5:56 PM Jordan Brown openscad@jordan.maileater.net
wrote:
On 10/28/2024 2:34 PM, Joe Weinpert via Discuss wrote:
I don't have an algorithm at all. I was looking for one, though :-)
Look at the sample pictures I sent as just being stl objects. What would
I need to do to create them in OpenSCAD? How do you create odd shaped
"blobs" and patterns and put them together?
polyhedron(), and math to come up with the desired shape.
Here's something I did to come up with a water wave pattern. It's not
great but it illustrates the idea. The bulk is the sfc() module, which is
like surface() but takes its input in the form of an array. surface()
really should do that, but doesn't and I haven't gotten around to making it
happen. I was never very happy with the relationship between the
resolution of the array and the size presented, so that may be more complex
than it needs to be.
For something like you describe, you need the sfc() module and a module
that produces the right height-map for your pattern.
$fa = 1;
$fs = 0.5;
waterX = 600;
waterY = 600;
waterStep = 5;
waveLengthX = 60;
waveLengthY = 50;
waveAmpX = 2;
waveAmpY = 1;
waveH = waveAmpX + waveAmpY;
baseH = waveH + 0.5;
function wave(x,y) = waveAmpXsin(360x/waveLengthX) + waveAmpYsin(360y/waveLengthY);
module water() {
water = [
let(nx = floor(waterX/waterStep))
let(xStep = waterX/nx)
let(ny = floor(waterY/waterStep))
let(yStep = waterY/ny)
for (ix = [0:nx]) [
for (iy=[0:ny])
wave(ixxStep, iyyStep)
]
];
translate([-waterX/4,-waterY/4,waveH])
sfc(water, [waterX, waterY, baseH]);
}
module sfc(a, sz) {
function dataIndex(x, y) = dataBase + x*ny + y;
nx = len(a);
ny = len(a[0]);
corners = 0;
dataBase = corners + 4;
pts = [
[0, 0, -sz.z],
[nx-1, 0, -sz.z],
[nx-1, ny-1, -sz.z],
[0, ny-1, -sz.z],
for (x = [0:nx-1])
for (y = [0:ny-1])
[ x, y, a[x][y] ]
];
faces = [
[ corners+0, corners+1, corners+2 ],
[ corners+0, corners+2, corners+3 ],
[
each for (x=[0:nx-1]) dataIndex(x,0),
corners+1,
corners+0,
],
[
each for (y=[0:ny-1]) dataIndex(nx-1,y),
corners+2,
corners+1,
],
[
each for (x=[nx-1:-1:0]) dataIndex(x,ny-1),
corners+3,
corners+2,
],
[
each for (y=[ny-1:-1:0]) dataIndex(0,y),
corners+0,
corners+3,
],
each for (x=[0:nx-2], y=[0:ny-2]) [
[ dataIndex(x+1, y), dataIndex(x, y), dataIndex(x, y+1) ],
[ dataIndex(x+1, y+1), dataIndex(x+1, y), dataIndex(x, y+1) ],
],
];
scale([sz.x/(nx-1),sz.y/(ny-1),1])
polyhedron(pts, faces, convexity=ceil(max(waterX/waveLengthX, waterY/waveLengthY)));
}
water();
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110 **
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a** is going up. -- Chris Hadfield about flying up the space shuttle.
** 'a' for accelleration.
Rogier, I would say the hard part of this problem is producing the set of
paths, not getting from that to the shape. I think if you have the set of
paths you can sweep them as in my example to create the shape.
I think solving the minimal surface problem (soap bubbles) is harder than
the algorithm you propose (which I didn't entirely understand). It's not
a local problem. But I also don't see how minimal surfaces are relevant
to this problem.
Here are examples of the desired output that appear like they were sent
directly to me and not to the list, so I'm repeating them:
[image: image.png]
[image: image.png]
On Tue, Oct 29, 2024 at 6:11 AM Rogier Wolff R.E.Wolff@bitwizard.nl wrote:
I didn't quite catch the beginning of this discussion. But maybe
interesting anyway....
Because programming an algorithm in openscad might be difficult it
might be better to just do it in python and then export to openscad
syntax.
GIVEN a set of 3D curves, find a surface that matches the
set-of-curves.
If you just randomly "do stuff" then things become a mess. What do I
mean with "matches". Well, if you give a human a point cloud or a
set-of-curves, we immediately imagine the object they belong to. How
to capture that mathematically? I'd think soap surface comes close:
Minimal area of the surface.
I think I have an algorithm that is possibly perfect, possibly
close-but-not-quite.
Between each pair of curves, for each linesegment on one find the
closest point to the linesegment on the other curve. I'm not sure if
you have to take the sum of the linesegments or the actual distance to
the line. That's a triangle of your surface. For "well behaved"
curves, this gives the optimal surface. If there are not "well
behaved" curves that give a surface with holes... I don't know.
So for Jordan's example you could pass in something like:
a=5;
for (i=[0:.3:50])
translate ([0,0,asin(i360*4/50)]) circle (r=i);
or the radials. In openscad you can create a list-of-points with a
sinewave as the Z coordinate in one go. But I haven't memorized the
syntax yet.
(Initially / forever it is NOT the task of the algorithm to figure out
which pairs of curves to use for the surface. The user will have to
pass them in in sequence).
Being able to define surfaces (2d objects in 3D), would eventually
allow users to stitch them together (like we can already with
triangles) and create 3D objects. My example above together with
cylinder-surface (top=false) would create a real 3D object.
Roger.
On Mon, Oct 28, 2024 at 07:06:25PM -0400, Adrian Mariano via Discuss wrote:
I don't think the waves problem gives much insight into the general
parametric problem that was posed. Producing that general parametric
pattern as a function over the xy plane seems like it might be difficult.
I suppose there might be some cool generative method that used an
iterative
process to produce a functional shape like that.
When I looked at it I thought maybe you could generate a set of paths for
each ridge (or cut, if you like). I thought maybe this could be turned
into a texture, but that's hard. So that leads to something like this
(where you might be able to get away regular path_sweep if there are more
gentle curves---it would be faster). But I have no clue how you
generate
the path list.
include<BOSL2/std.scad>
cuboid([10,10,1],anchor=TOP+LEFT);
cycles=3;
path = [for(t=[0:10:360cycles]) [10t/360/cycles,
(1+t/(360*cycles)/.5)*sin(t)]];
profile = [for(theta=[-180:36:180]) [theta/180/3, (1+cos(theta))/7]];
path_sweep2d(profile, path);
[image: image.png]
On Mon, Oct 28, 2024 at 5:56 PM Jordan Brown <
wrote:
On 10/28/2024 2:34 PM, Joe Weinpert via Discuss wrote:
I don't have an algorithm at all. I was looking for one, though :-)
Look at the sample pictures I sent as just being stl objects. What
would
I need to do to create them in OpenSCAD? How do you create odd shaped
"blobs" and patterns and put them together?
polyhedron(), and math to come up with the desired shape.
Here's something I did to come up with a water wave pattern. It's not
great but it illustrates the idea. The bulk is the sfc() module,
which is
like surface() but takes its input in the form of an array. surface()
really should do that, but doesn't and I haven't gotten around to
making it
happen. I was never very happy with the relationship between the
resolution of the array and the size presented, so that may be more
complex
than it needs to be.
For something like you describe, you need the sfc() module and a module
that produces the right height-map for your pattern.
$fa = 1;
$fs = 0.5;
waterX = 600;
waterY = 600;
waterStep = 5;
waveLengthX = 60;
waveLengthY = 50;
waveAmpX = 2;
waveAmpY = 1;
waveH = waveAmpX + waveAmpY;
baseH = waveH + 0.5;
function wave(x,y) = waveAmpXsin(360x/waveLengthX) +
waveAmpYsin(360y/waveLengthY);
module water() {
water = [
let(nx = floor(waterX/waterStep))
let(xStep = waterX/nx)
let(ny = floor(waterY/waterStep))
let(yStep = waterY/ny)
for (ix = [0:nx]) [
for (iy=[0:ny])
wave(ixxStep, iyyStep)
]
];
translate([-waterX/4,-waterY/4,waveH])
sfc(water, [waterX, waterY, baseH]);
}
module sfc(a, sz) {
function dataIndex(x, y) = dataBase + x*ny + y;
nx = len(a);
ny = len(a[0]);
corners = 0;
dataBase = corners + 4;
pts = [
[0, 0, -sz.z],
[nx-1, 0, -sz.z],
[nx-1, ny-1, -sz.z],
[0, ny-1, -sz.z],
for (x = [0:nx-1])
for (y = [0:ny-1])
[ x, y, a[x][y] ]
];
faces = [
[ corners+0, corners+1, corners+2 ],
[ corners+0, corners+2, corners+3 ],
[
each for (x=[0:nx-1]) dataIndex(x,0),
corners+1,
corners+0,
],
[
each for (y=[0:ny-1]) dataIndex(nx-1,y),
corners+2,
corners+1,
],
[
each for (x=[nx-1:-1:0]) dataIndex(x,ny-1),
corners+3,
corners+2,
],
[
each for (y=[ny-1:-1:0]) dataIndex(0,y),
corners+0,
corners+3,
],
each for (x=[0:nx-2], y=[0:ny-2]) [
[ dataIndex(x+1, y), dataIndex(x, y), dataIndex(x, y+1) ],
[ dataIndex(x+1, y+1), dataIndex(x+1, y), dataIndex(x,
y+1) ],
],
];
scale([sz.x/(nx-1),sz.y/(ny-1),1])
polyhedron(pts, faces, convexity=ceil(max(waterX/waveLengthX,
waterY/waveLengthY)));
}
water();
--
** R.E.Wolff@BitWizard.nl ** https://www.BitWizard.nl/ ** +31-15-2049110
**
** Delftechpark 11 2628 XJ Delft, The Netherlands. KVK: 27239233 **
f equals m times a. When your f is steady, and your m is going down
your a** is going up. -- Chris Hadfield about flying up the space shuttle.
** 'a' for accelleration.