Rendering Polygon Mesh using CGAL...

ERROR: CGAL error in CGALUtils::applyUnion3D: CGAL ERROR: assertion
violation! Expr: itl != it->second.end() File:
/mxe/usr/x86_64-w64-mingw32.static.posix/include/CGAL/Nef_3/SNC_external_structure.h
Line: 1152

Geometries in cache: 155

Geometry cache size in bytes: 2750192

CGAL Polyhedrons in cache: 1

CGAL cache size in bytes: 11344

Total rendering time: 0:00:43.942

Top level object is a 3D object:

Simple: yes

Vertices: 8

Halfedges: 24

Edges: 12

Halffacets: 12

Facets: 6

Volumes: 2

Rendering finished.

Any ideas?

Joe Weinpert
joe.weinpert@gmail.com
www.jwstudio.art http://jwstudio.art

Joe sent me a copy of the .SCAD file.  It uses a library called
Pathbuilder to turn an SVG string into points, and then for each
individual shape uses BOSL2's "skin" to connect the shape to a small
circle below the centroid of the shape, to produce sort of an inverted
cone.  Those are then subtracted from a cuboid.

The problem is in BOSL2's "skin" operation; in some cases it produces a
twisted polyhedron.

There may be multiple shapes with the same problem, but here's one that
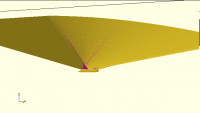
I isolated, shown as a positive shape in View/Thrown Together mode.
Purple is bad.  This one is ptsTop[3]; it derives from the SVG data
starting with "M 9.039759,2.403697".

skin() has several "methods" for how it connects the shapes.  The
default is "direct".  Perhaps one of the other methods would produce
better results.

Because these shapes are all convex (I think), you might be able to use
hull() instead of skin().  The most straightforward way to do that is to
extrude the top and bottom shapes a little, and then hull them.  A less
straightforward way is to generate a polyhedron using all of the points

• doesn't matter if they are connected or result in a valid polyhedron -
  and hull that.

Other notes:

• Pathbuilder parses SVG data using OpenSCAD user functions.  That's
  impressive but very very slow.  It should be much faster to put the
  SVG data into a separate SVG file and have OpenSCAD import() it.
• The inverted cones have their tops exactly at the top of the cuboid
  they are being subtracted from, and their points exactly at the
  bottom.  That produces nasty Z-fighting.  It's usually best to have
  negative objects protrude slightly outside the object they are being
  subtracted from, if they're intended to cut through.  It looks to me
  like the shapes should be lifted just a tad so that they are above
  the cuboid, and maybe make the cuboid a little taller (which makes
  it project further down because of the anchor used) so that when you
  print you get at least a layer or two across the points.
• It's possible that Manifold would handle this better, but I didn't
  try because the shape that results isn't correct even if the
  rendering engine can handle it.

How I diagnosed this:

• I noticed the Z-fighting and fixed it; that didn't fix the CGAL problem.
• I isolated a problematic shape by binary search - the problem
  demonstrated with shapes 0-74; did it demonstrate with 0-37?  0-18? 
  Et cetera.
• I broke up the SVG text into individual shapes by breaking before
  the "M" entries, turning it into str(shape, shape, shape, ...) so
  that I could comment out individual shapes.
• For some reason I still didn't see the purple (perhaps because the
  tan color overrode Thrown Together's color scheme, and perhaps
  because it was small and I didn't look closely enough and was
  looking at the results after the difference rather than looking
  directly at the negative object.)
• I further broke that shape apart into line segments, again using a
  binary search to get down to a modest number of line segments that
  demonstrated the problem.
• I stripped the program down to pretty much just the skin and those
  points, and then I saw the purple.
• I backed up and reproduced the problem with the original shape.