Surface interpolation and BREP-style design with OpenSCAD
I am interested in this, where can I find the library?
I recently add support in the FreeCAD OpenSCAD Alternate import for
minkowski requests that have the second object as a Sphere or a cylinder
seehttps://github.com/KeithSloan/OpenSCAD_Alt_Import.
(Embarrassingly I had created a branch two years ago but never got round to merging :-()
I am also looking at a facility to access libraries direct from the FreeCAD OpenSCAD workbench.
On testing with BOSL the exampleshttps://github.com/revarbat/BOSL
Says
cuboid([20,20,30], fillet=5, edges=EDGES_Z_ALL); Produces
minkowski() {cube([10,10,20], center=true); sphere(r=5, $fn=32);} Which would mean the importer would create a FreeCAD Brep Object with Fillets
but on testing I see
include <BOSL/shapes.scad>
cuboid([20,20,30], fillet=5);
Produces as CSG
group() {
group() {
group() {
group() {
group();
}
}
multmatrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]) {
group() {
group() {
group() {
minkowski(convexity = 0) {
cube(size = [10, 10, 20], center = true);
group() {
rotate_extrude(angle = 360, convexity = 2, $fn = 16, $fa = 12, $fs = 2) {
polygon(points = [[0, -5.09796], [1.9509, -4.7099], [3.6048, -3.6048], [4.7099, -1.9509], [5.09796, 0], [4.7099, 1.9509], [3.6048, 3.6048], [1.9509, 4.7099], [0, 5.09796]], paths = undef, convexity = 1);
}
}
}
}
}
}
}
}
}
Very disappointing.
Message: 7
Date: Tue, 28 Feb 2023 02:10:45 +0100
From: Martin HerdieckerhoffMartin.Herdieckerhoff@mnet-mail.de
Subject: [OpenSCAD] Surface interpolation and BREP-style design with
OpenSCAD
To:discuss@lists.openscad.org
Message-ID:64556bd1-741f-2be5-06e0-b1ef9696e0ec@mnet-mail.de
Content-Type: multipart/alternative;
boundary="------------70wlakPuCtjOQNWaPgebolRa"
In the desire to provide a safe, easy and intuitive way to create
aesthetically rounded organic forms in OpenSCAD, I developed a library
called 'Yari'. Some of its features are visually presented here. In the
literature which was accessible to me, I did not find what I was looking
for. Therefore all of the used approaches (except for the VFH) are based
on my own thinking and experiments rather than on published papers.
I would classify the resulting approach as an interpolating, geometric,
bivariate, iterative subdivision scheme for PNs (Points with Normals). A
related recent paper of Yang, Xunnian is "Point-Normal Subdivision
Curves and Surfaces" (preprint, v2 of Dec. 2022, [2210.07974] on
arXiv.org). It describes similar goals and produces partially similar
results but the used approach is totally different from mine. One
difference is that the Yari library handles S-shaped boundary conditions
without any problem (compare the discussion of inflections in the cited
paper). Another difference is that the approach taken with Yari is
iterative rather than recursive. Accordingly, refinement is not
restricted to powers of two. This reminds more to NURBS than to
traditional subdivision schemes.
Yari aggregates patches (e.g. curved triangles and quads) to surfaces
with borders or to closed surfaces. These aggregates are held in a
half-edge data structure called VFH (Vertices, Faces and Half-edges) as
BREP. The VFH keeps also the normals. An OpenSCAD polyhedron can be
turned into a VFH and a VFH can be interpolated into an OpenSCAD polyhedron.
Attached images:
*xing_test
Input: Four points with simple and intuitive unit normals.
*Output: *The quad patch is interpolated and replicated 32 times.
This gives a system of sprues with perfectly circular cross sections
and with perfectly sine-shaped longitudinal cuts. The sprues form
perfectly circular holes.
-
torus_test_3x3
*Input: *3x3 points with normals, regularly placed on a torus.
Output: The nine patches interpolate to a perfect torus.
*pyramid_test
*Input: *An irregular pyramid made of four triangles and a quad. All
of its corners are on a sphere and the unit normals are taken
directly from the points.
Output: The pyramid interpolates to a perfect sphere.
*tripod_from_PDRAs
*Input: *Three points with unit directions, radii and (negative or
positive) opening angles.
*Output: *A smooth bordered surface spanned by the given pod ends.
By the way, symmetric, parallel, diverging pods with other lengs of
legs work as well.
Originally the purpose of this library was to design some jewelry.
Meanwhile I think that the library might be of worth in its own right.
What do experts here think about the shown features?
What would you suggest me to do with the developed algorithms?
-- Martin
--
========== Art & Ceramics ===========
https://www.instagram.com/ksloan1952/
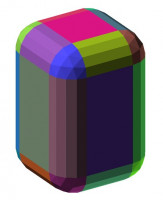
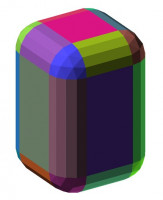
The equivalent of cuboid([20,20,30], fillet=5) created from patches with
my library looks like this
and produces a CSG with this structure:
group() {
group() {
multmatrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0,
1]]) {
group() {
group() {
group() {
group() {
polyhedron(points = [...], faces = [...], convexity = 2);
}
}
}
}
group() {
group();
}
}
}
}
Am 28.02.2023 um 09:01 schrieb Keith Sloan:
I recently add support in the FreeCAD OpenSCAD Alternate import for
minkowski requests that have the second object as a Sphere or a cylinder
seehttps://github.com/KeithSloan/OpenSCAD_Alt_Import.
(Embarrassingly I had created a branch two years ago but never got round to merging :-()
I am also looking at a facility to access libraries direct from the FreeCAD OpenSCAD workbench.
On testing with BOSL the exampleshttps://github.com/revarbat/BOSL
Says
cuboid([20,20,30], fillet=5, edges=EDGES_Z_ALL); Produces
minkowski() {cube([10,10,20], center=true); sphere(r=5, $fn=32);} Which would mean the importer would create a FreeCAD Brep Object with Fillets
but on testing I see
include <BOSL/shapes.scad>
cuboid([20,20,30], fillet=5);
Produces as CSG
group() {
group() {
group() {
group() {
group();
}
}
multmatrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]) {
group() {
group() {
group() {
minkowski(convexity = 0) {
cube(size = [10, 10, 20], center = true);
group() {
rotate_extrude(angle = 360, convexity = 2, $fn = 16, $fa = 12, $fs = 2) {
polygon(points = [[0, -5.09796], [1.9509, -4.7099], [3.6048, -3.6048], [4.7099, -1.9509], [5.09796, 0], [4.7099, 1.9509], [3.6048, 3.6048], [1.9509, 4.7099], [0, 5.09796]], paths = undef, convexity = 1);
}
}
}
}
}
}
}
}
}
@Adrian Mariano
Strangely I see your reply on https://lists.openscad.org/empathy/ but
not in my inbox from the mailing list.
I found approximative subdivision schemes - like e.g. the one you
mention - not satisfying for OpenSCAD.
The BOSL2 library is great and I agree that it indeed looks like a good
home for enhancements like mine.
The work of Ronaldo on VNFext could have been an excellent start into
the assembly of patches.
For me the assembly of patches proved to be a good, stepwise,
well-debuggable process with safe (2-manifold) results.
What challenges regarding usability / practicality of rounded polyhedra
did you encounter?
Am 28.02.2023 schrieb Adrian Mariano:
Your method looks very interesting. I've long had an interest in
implementing curves and have been working in the BOSL2 library to do
this.
If you're looking for a home for your algorithms, it might be
appropriate
to add them to BOSL2. I explored using Catmull and Ronaldo explored
some
other similar methods, but it wasn't clear that any of our approaches
were
sufficiently usable to be practical. But we took a different
approach of
starting with a polyhedron and trying to smooth it.
It's been a couple years since I worked on it, but I recall the
difficulties with the subdivision schemes being that they were hard to
control, so getting a desired amount of rounding was not always possible.
And they were also very sensitive to exactly how a polyhedron was
triangulated, which is something that's generally invisible to you when you
examine a polyhedron in OpenSCAD. I think they may also have been on the
slow side, especially if you wanted to do several iterations, or operate on
a polyhedron with many faces. There was no difficulty in maintaining
validity of the 2-manifold with the subdivision approaches. That is, valid
input lead automatically to valid output. But then there's also the
problem that you need to actually have the polyhedron you want to operate
on available as a list of faces and vertices, which can be a challenge for
more interesting cases.
You scheme looks like it is more usable because you are able to build
interesting polyhedra from very short descriptions, though from your
examples I don't really understand the exact capabilities and limits of
your approach and implementation. One of the things that we (the BOSL2
authors) have wondered about is how to enable people to make 3d bezier
patches that are actually useful. Your method isn't bezier based, but it
seems like it is an approach to that basic problem of how to create 3d
structures.
On Tue, Feb 28, 2023 at 8:14 PM Martin Herdieckerhoff <
Martin.Herdieckerhoff@mnet-mail.de> wrote:
@Adrian Mariano
Strangely I see your reply on https://lists.openscad.org/empathy/ but not
in my inbox from the mailing list.
I found approximative subdivision schemes - like e.g. the one you mention
- not satisfying for OpenSCAD.
The BOSL2 library is great and I agree that it indeed looks like a good
home for enhancements like mine.
The work of Ronaldo on VNFext could have been an excellent start into the
assembly of patches.
For me the assembly of patches proved to be a good, stepwise,
well-debuggable process with safe (2-manifold) results.
What challenges regarding usability / practicality of rounded polyhedra
did you encounter?
Am 28.02.2023 schrieb Adrian Mariano:
Your method looks very interesting. I've long had an interest in
implementing curves and have been working in the BOSL2 library to do
this.
If you're looking for a home for your algorithms, it might be
appropriate
to add them to BOSL2. I explored using Catmull and Ronaldo explored
some
other similar methods, but it wasn't clear that any of our approaches
were
sufficiently usable to be practical. But we took a different approach
of
starting with a polyhedron and trying to smooth it.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
I agree that Martin's method is very exciting, but I am not clear how
easy it is to predict the object that will result given the small number
of input parameters. That is, I'm not sure how easy it will be to "drive".
On 2/28/2023 8:45 PM, Adrian Mariano wrote:
It's been a couple years since I worked on it, but I recall the
difficulties with the subdivision schemes being that they were hard to
control, so getting a desired amount of rounding was not always
possible. And they were also very sensitive to exactly how a
polyhedron was triangulated, which is something that's generally
invisible to you when you examine a polyhedron in OpenSCAD. I think
they may also have been on the slow side, especially if you wanted to
do several iterations, or operate on a polyhedron with many faces.
There was no difficulty in maintaining validity of the 2-manifold with
the subdivision approaches. That is, valid input lead automatically
to valid output. But then there's also the problem that you need to
actually have the polyhedron you want to operate on available as a
list of faces and vertices, which can be a challenge for more
interesting cases.
You scheme looks like it is more usable because you are able to build
interesting polyhedra from very short descriptions, though from your
examples I don't really understand the exact capabilities and limits
of your approach and implementation. One of the things that we (the
BOSL2 authors) have wondered about is how to enable people to make 3d
bezier patches that are actually useful. Your method isn't bezier
based, but it seems like it is an approach to that basic problem of
how to create 3d structures.
On Tue, Feb 28, 2023 at 8:14 PM Martin Herdieckerhoff
Martin.Herdieckerhoff@mnet-mail.de wrote:
@Adrian Mariano
Strangely I see your reply on https://lists.openscad.org/empathy/
but not in my inbox from the mailing list.
I found approximative subdivision schemes - like e.g. the one you
mention - not satisfying for OpenSCAD.
The BOSL2 library is great and I agree that it indeed looks like a
good home for enhancements like mine.
The work of Ronaldo on VNFext could have been an excellent start
into the assembly of patches.
For me the assembly of patches proved to be a good, stepwise,
well-debuggable process with safe (2-manifold) results.
What challenges regarding usability / practicality of rounded
polyhedra did you encounter?
Am 28.02.2023 schrieb Adrian Mariano:
Your method looks very interesting. I've long had an interest in
implementing curves and have been working in the BOSL2 library
to do this.
If you're looking for a home for your algorithms, it might be
appropriate
to add them to BOSL2. I explored using Catmull and Ronaldo
explored some
other similar methods, but it wasn't clear that any of our
approaches were
sufficiently usable to be practical. But we took a different
approach of
starting with a polyhedron and trying to smooth it.
_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email todiscuss-leave@lists.openscad.org
It seems like if you can specify circles and it makes a joint with your
circles as its edge that's pretty easy to understand. The other cases seem
less obvious.
On Tue, Feb 28, 2023 at 9:26 PM jon jon@jonbondy.com wrote:
I agree that Martin's method is very exciting, but I am not clear how easy
it is to predict the object that will result given the small number of
input parameters. That is, I'm not sure how easy it will be to "drive".
On 2/28/2023 8:45 PM, Adrian Mariano wrote:
It's been a couple years since I worked on it, but I recall the
difficulties with the subdivision schemes being that they were hard to
control, so getting a desired amount of rounding was not always possible.
And they were also very sensitive to exactly how a polyhedron was
triangulated, which is something that's generally invisible to you when you
examine a polyhedron in OpenSCAD. I think they may also have been on the
slow side, especially if you wanted to do several iterations, or operate on
a polyhedron with many faces. There was no difficulty in maintaining
validity of the 2-manifold with the subdivision approaches. That is, valid
input lead automatically to valid output. But then there's also the
problem that you need to actually have the polyhedron you want to operate
on available as a list of faces and vertices, which can be a challenge for
more interesting cases.
You scheme looks like it is more usable because you are able to build
interesting polyhedra from very short descriptions, though from your
examples I don't really understand the exact capabilities and limits of
your approach and implementation. One of the things that we (the BOSL2
authors) have wondered about is how to enable people to make 3d bezier
patches that are actually useful. Your method isn't bezier based, but it
seems like it is an approach to that basic problem of how to create 3d
structures.
On Tue, Feb 28, 2023 at 8:14 PM Martin Herdieckerhoff <
Martin.Herdieckerhoff@mnet-mail.de> wrote:
@Adrian Mariano
Strangely I see your reply on https://lists.openscad.org/empathy/ but
not in my inbox from the mailing list.
I found approximative subdivision schemes - like e.g. the one you mention
- not satisfying for OpenSCAD.
The BOSL2 library is great and I agree that it indeed looks like a good
home for enhancements like mine.
The work of Ronaldo on VNFext could have been an excellent start into the
assembly of patches.
For me the assembly of patches proved to be a good, stepwise,
well-debuggable process with safe (2-manifold) results.
What challenges regarding usability / practicality of rounded polyhedra
did you encounter?
Am 28.02.2023 schrieb Adrian Mariano:
Your method looks very interesting. I've long had an interest in
implementing curves and have been working in the BOSL2 library to do
this.
If you're looking for a home for your algorithms, it might be
appropriate
to add them to BOSL2. I explored using Catmull and Ronaldo explored
some
other similar methods, but it wasn't clear that any of our approaches
were
sufficiently usable to be practical. But we took a different approach
of
starting with a polyhedron and trying to smooth it.
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
The reason BOSL is making a more complex CSG, is so that the sphere used for Minkowski has its vertices better aligned to the axes of the cube. That makes a much better looking triangulation of the corners in base OpenSCAD.
-Revar
On Feb 28, 2023, at 6:49 PM, Adrian Mariano <avm4@cornell.edu> wrote:
It seems like if you can specify circles and it makes a joint with your circles as its edge that's pretty easy to understand. The other cases seem less obvious.
On Tue, Feb 28, 2023 at 9:26 PM jon <jon@jonbondy.com> wrote:
I agree that Martin's method is very exciting, but I am not clear how easy it is to predict the object that will result given the small number of input parameters. That is, I'm not sure how easy it will be to "drive".
On 2/28/2023 8:45 PM, Adrian Mariano wrote:
It's been a couple years since I worked on it, but I recall the difficulties with the subdivision schemes being that they were hard to control, so getting a desired amount of rounding was not always possible. And they were also very sensitive to exactly how a polyhedron was triangulated, which is something that's generally invisible to you when you examine a polyhedron in OpenSCAD. I think they may also have been on the slow side, especially if you wanted to do several iterations, or operate on a polyhedron with many faces. There was no difficulty in maintaining validity of the 2-manifold with the subdivision approaches. That is, valid input lead automatically to valid output. But then there's also the problem that you need to actually have the polyhedron you want to operate on available as a list of faces and vertices, which can be a challenge for more interesting cases.
You scheme looks like it is more usable because you are able to build interesting polyhedra from very short descriptions, though from your examples I don't really understand the exact capabilities and limits of your approach and implementation. One of the things that we (the BOSL2 authors) have wondered about is how to enable people to make 3d bezier patches that are actually useful. Your method isn't bezier based, but it seems like it is an approach to that basic problem of how to create 3d structures.
On Tue, Feb 28, 2023 at 8:14 PM Martin Herdieckerhoff <Martin.Herdieckerhoff@mnet-mail.de> wrote:
@Adrian Mariano
Strangely I see your reply on https://lists.openscad.org/empathy/ but not in my inbox from the mailing list.
I found approximative subdivision schemes - like e.g. the one you mention - not satisfying for OpenSCAD.
The BOSL2 library is great and I agree that it indeed looks like a good home for enhancements like mine.
The work of Ronaldo on VNFext could have been an excellent start into the assembly of patches.
For me the assembly of patches proved to be a good, stepwise, well-debuggable process with safe (2-manifold) results.
What challenges regarding usability / practicality of rounded polyhedra did you encounter?Am 28.02.2023 schrieb Adrian Mariano:
> Your method looks very interesting. I've long had an interest in
> implementing curves and have been working in the BOSL2 library to do this.
> If you're looking for a home for your algorithms, it might be appropriate
> to add them to BOSL2. I explored using Catmull and Ronaldo explored some
> other similar methods, but it wasn't clear that any of our approaches were
> sufficiently usable to be practical. But we took a different approach of
> starting with a polyhedron and trying to smooth it._______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org_______________________________________________ OpenSCAD mailing list To unsubscribe send an email to <a href="mailto:discuss-leave@lists.openscad.org" target="_blank">discuss-leave@lists.openscad.org</a>_______________________________________________
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
Looks interesting
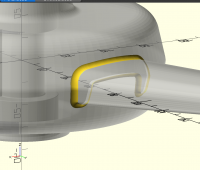
Can you do fillets at the intersection of 2 solids?
example:
[image: Screenshot 2023-03-01 at 10.38.18 PM.png]
If you can do that then it would really help.
I have also tried rounding various intersecting surfaces, but it is quite
complicated many times and no generic solution at the moment.
On Wed, 1 Mar 2023 at 05:51, Martin Herdieckerhoff <
Martin.Herdieckerhoff@mnet-mail.de> wrote:
The equivalent of cuboid([20,20,30], fillet=5) created from patches with
my library looks like this
and produces a CSG with this structure:
group() {
group() {
multmatrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0,
1]]) {
group() {
group() {
group() {
group() {
polyhedron(points = [...], faces = [...],
convexity = 2);
}
}
}
}
group() {
group();
}
}
}
}
Am 28.02.2023 um 09:01 schrieb Keith Sloan:
I recently add support in the FreeCAD OpenSCAD Alternate import for
minkowski requests that have the second object as a Sphere or a cylinder
see https://github.com/KeithSloan/OpenSCAD_Alt_Import.
(Embarrassingly I had created a branch two years ago but never got round to merging :-()
I am also looking at a facility to access libraries direct from the FreeCAD OpenSCAD workbench.
On testing with BOSL the examples https://github.com/revarbat/BOSL
Says
cuboid([20,20,30], fillet=5, edges=EDGES_Z_ALL);
Produces minkowski() {cube([10,10,20], center=true); sphere(r=5, $fn=32);}
Which would mean the importer would create a FreeCAD Brep Object with Fillets
but on testing I see
include <BOSL/shapes.scad>
cuboid([20,20,30], fillet=5);
Produces as CSG
group() {
group() {
group() {
group() {
group();
}
}
multmatrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]) {
group() {
group() {
group() {
minkowski(convexity = 0) {
cube(size = [10, 10, 20], center = true);
group() {
rotate_extrude(angle = 360, convexity = 2, $fn = 16, $fa = 12, $fs = 2) {
polygon(points = [[0, -5.09796], [1.9509, -4.7099], [3.6048, -3.6048], [4.7099, -1.9509], [5.09796, 0], [4.7099, 1.9509], [3.6048, 3.6048], [1.9509, 4.7099], [0, 5.09796]], paths = undef, convexity = 1);
}
}
}
}
}
}
}
}
}
OpenSCAD mailing list
To unsubscribe send an email to discuss-leave@lists.openscad.org
@ Adrian Mariano
thank you very much for your interesting feedback on the subdivision
schemes that you tried for OpenSCAD some years ago.
I willl try to clarify my approach in the light of your remarks below.
It's been a couple years since I worked on it, but I recall the
difficulties with the subdivision schemes being that they were hard to
control, so getting a desired amount of rounding was not always
possible. And they were also very sensitive to exactly how a
polyhedron was triangulated, which is something that's generally
invisible to you when you examine a polyhedron in OpenSCAD. I think
they may also have been on the slow side, especially if you wanted to
do several iterations, or operate on a polyhedron with many faces.
There was no difficulty in maintaining validity of the 2-manifold with
the subdivision approaches. That is, valid input lead automatically
to valid output. But then there's also the problem that you need to
actually have the polyhedron you want to operate on available as a
list of faces and vertices, which can be a challenge for more
interesting cases.
You scheme looks like it is more usable because you are able to build
interesting polyhedra from very short descriptions, though from your
examples I don't really understand the exact capabilities and limits
of your approach and implementation. One of the things that we (the
BOSL2 authors) have wondered about is how to enable people to make 3d
bezier patches that are actually useful. Your method isn't bezier
based, but it seems like it is an approach to that basic problem of
how to create 3d structures.
"hard to control": True for approximating schemes which throw away all
input in each step of the recursive process. My scheme is interpolating
and iterative. The surface runs exactly through the given points with
exactly the given normals and/or tangents. You interpolate in a fixed
number of steps, no matter what granularity you want. Thinking in points
with normals seems very intuitive for me - that means easy to control
with your mind.
"desired amount of rounding": From the cuboid example (Keith Sloan) you
see that the rounding is as intuitive as it can get: You stay away from
the rounded corner by the radius of rounding. Done.
"sensitive to the exact triangulation": Indeed some of the more widely
used approximative subdivision schemes have that issue. After looking
into some papers dealing with difficulties near "extraordinary
vertcices" with higher valence (number of incident faces) I decided to
approach the problem in a different way. My method is highly (if not
completely) insensitive to the triangulation. For those familiar with
the problems this should be clear to see from the image of the cuboid
(in a recent post).
"on the slow side": As we all know this is generally a problem with
OpenSCAD. Due to its iterative nature I assume my approach to do better
than the approximating schemes. A hugh advantage with respect to
performance is also that you can split into exactly the required amount
of mn quads (or similar with triangles) - you are not bound to split
into (2**k)(2**k) quads.
"maintaining validity of the 2-manifold": No issue? Maybe not when you
subdivide (watertight, non-degenerate) polyhedra. I use degenerate
polyhedra (face soups) all the time. Assembly of those is very
interesting. You must transitionally give up 2-manifoldness but you want
to have it in the end. You want the assembly to be easy, tolerant, fast
and safe which is quite a challenge. You can make any number of mistakes
regarding order of points (clockwise or not), normals, directions to
neighbours etc. and you can get all sorts of funny results - at best
visually or otherwise in the console window ... A good and reliable
half-edge data structure is the key to successfully handle bunches of
patches with attached directions.
"exact capabilities and limits of your approach": Well, that is what I
try to clarify with my postings. Think of the assembly of patches to
polyhedra within a half-edge data structure. Add (or automatically
compute) normals to the vertices. Add (or automatically compute)
directions to neighbour vertices. These tangents are orthogonal to
normals but they do not need to go there on the shortest way). Add a
number of intervals to each edge (with some restrictions, such as e.g.
an mnm*n scheme for a quad). Now interpolate each face and put the
result back into a VNF and from there into an OpenSCAD polyhedron. When
the input polyhedron was watertight than the output will be watertight
as well.
"3d bezier patches": Cubic bezier patches is what I tried first.
Eventually I found out that it is impossible to get smooth seams between
those from PNs - unless you use Beziers of order 6 when I remember
correctly. It was a nightmare to set the inner control points properly -
because it is impossible to solve the PN interpolation problem smoothly
with cubic Beziers. With my method I get smoother and rounder surfaces
from less and more intuitive input.
As far as I have seen, you have not explained details of your approach, so
I really don't know much about it. With the subdivision approaches, the
amount of rounding is determined by the triangulation and the number of
iterations applied. So you can't specify that you want a certain radius,
for example. That was a limitation.
I agree that a method that works on 2-manifolds with holes is desirable so
that you can assemble a model from parts by "gluing" pieces together at the
holes. I never tried to make the subdivision methods work on input like
that. It seems like it would be necessary to identify the edges at the
hole and treat them in some special way to keep them fixed. But since I
never pursued these methods, I didn't look into it. It seems like you have
an interesting method that appears promising and I have methods I abandoned
because they didn't seem promising, so we don't need to discuss my
abandoned approaches at length. Regarding your approach, for example, what
is the half edge data structure you use? Ronaldo had worked on developing
an enriched VNF data structure that included additional adjacency
information.
I don't think assembly of parts is particularly difficult. Your paragraph
suggests to me more complications, but assuming I construct an incomplete
2-manifold patch it is easy and fast to assemble it together with other two
manifolds (e.g. what vnf_join() does in BOSL2.) However, this does not
produce an optimal output---there will be duplicate points, for example.
Depending on what downstream processing may occur, this can be OK or more
of a problem.
Cubic bezier patches seem to be quite weak. I did a bunch of development
with 4th order bezier patches, which can achieve continuous curvature
joints. I am not sure why you needed 6th order. Is it possible you tried
to work with triangular patches instead of quadrilateral ones? Ronaldo
looked into those and they seemed to be much more constrained and difficult
to use. I do not see where you define what PN means and do not know what
PN interpolation is. It's easy to create continuous curvature joints with
4th order beziers across edges. The required constraints are easy to
understand and easy to establish. But the problem I struggled with was
how to organize that in a way that creates a useful object. The methods I
have are based on modifying an existing defined object rather than creating
an object de novo. See for example
https://github.com/revarbat/BOSL2/wiki/rounding.scad#functionmodule-rounded_prism
https://github.com/revarbat/BOSL2/wiki/rounding.scad#functionmodule-join_prism
On Wed, Mar 1, 2023 at 12:58 PM Martin Herdieckerhoff <
Martin.Herdieckerhoff@mnet-mail.de> wrote:
@ Adrian Mariano
thank you very much for your interesting feedback on the subdivision
schemes that you tried for OpenSCAD some years ago.
I willl try to clarify my approach in the light of your remarks below.
It's been a couple years since I worked on it, but I recall the
difficulties with the subdivision schemes being that they were hard to
control, so getting a desired amount of rounding was not always
possible. And they were also very sensitive to exactly how a
polyhedron was triangulated, which is something that's generally
invisible to you when you examine a polyhedron in OpenSCAD. I think
they may also have been on the slow side, especially if you wanted to
do several iterations, or operate on a polyhedron with many faces.
There was no difficulty in maintaining validity of the 2-manifold with
the subdivision approaches. That is, valid input lead automatically
to valid output. But then there's also the problem that you need to
actually have the polyhedron you want to operate on available as a
list of faces and vertices, which can be a challenge for more
interesting cases.
You scheme looks like it is more usable because you are able to build
interesting polyhedra from very short descriptions, though from your
examples I don't really understand the exact capabilities and limits
of your approach and implementation. One of the things that we (the
BOSL2 authors) have wondered about is how to enable people to make 3d
bezier patches that are actually useful. Your method isn't bezier
based, but it seems like it is an approach to that basic problem of
how to create 3d structures.
"hard to control": True for approximating schemes which throw away all
input in each step of the recursive process. My scheme is interpolating
and iterative. The surface runs exactly through the given points with
exactly the given normals and/or tangents. You interpolate in a fixed
number of steps, no matter what granularity you want. Thinking in points
with normals seems very intuitive for me - that means easy to control
with your mind.
"desired amount of rounding": From the cuboid example (Keith Sloan) you
see that the rounding is as intuitive as it can get: You stay away from
the rounded corner by the radius of rounding. Done.
"sensitive to the exact triangulation": Indeed some of the more widely
used approximative subdivision schemes have that issue. After looking
into some papers dealing with difficulties near "extraordinary
vertcices" with higher valence (number of incident faces) I decided to
approach the problem in a different way. My method is highly (if not
completely) insensitive to the triangulation. For those familiar with
the problems this should be clear to see from the image of the cuboid
(in a recent post).
"on the slow side": As we all know this is generally a problem with
OpenSCAD. Due to its iterative nature I assume my approach to do better
than the approximating schemes. A hugh advantage with respect to
performance is also that you can split into exactly the required amount
of mn quads (or similar with triangles) - you are not bound to split
into (2**k)(2**k) quads.
"maintaining validity of the 2-manifold": No issue? Maybe not when you
subdivide (watertight, non-degenerate) polyhedra. I use degenerate
polyhedra (face soups) all the time. Assembly of those is very
interesting. You must transitionally give up 2-manifoldness but you want
to have it in the end. You want the assembly to be easy, tolerant, fast
and safe which is quite a challenge. You can make any number of mistakes
regarding order of points (clockwise or not), normals, directions to
neighbours etc. and you can get all sorts of funny results - at best
visually or otherwise in the console window ... A good and reliable
half-edge data structure is the key to successfully handle bunches of
patches with attached directions.
"exact capabilities and limits of your approach": Well, that is what I
try to clarify with my postings. Think of the assembly of patches to
polyhedra within a half-edge data structure. Add (or automatically
compute) normals to the vertices. Add (or automatically compute)
directions to neighbour vertices. These tangents are orthogonal to
normals but they do not need to go there on the shortest way). Add a
number of intervals to each edge (with some restrictions, such as e.g.
an mnm*n scheme for a quad). Now interpolate each face and put the
result back into a VNF and from there into an OpenSCAD polyhedron. When
the input polyhedron was watertight than the output will be watertight
as well.
"3d bezier patches": Cubic bezier patches is what I tried first.
Eventually I found out that it is impossible to get smooth seams between
those from PNs - unless you use Beziers of order 6 when I remember
correctly. It was a nightmare to set the inner control points properly -
because it is impossible to solve the PN interpolation problem smoothly
with cubic Beziers. With my method I get smoother and rounder surfaces
from less and more intuitive input.